随机共振在谐振接地系统故障选线中的应用
2020-11-03赵雅琳赵兴勇
赵雅琳,赵兴勇,宋 丽
(山西大学 电力工程系,太原030013)
国内配电网发生单相接地故障的概率最高,现有选线方法原理上都是利用故障线路与正常线路中所流过的零序电流幅值相差较大且相位相反的特征进行选线。 谐振接地系统在采用过补偿方式时,故障线路中所流过的零序电流幅值可能会小于正常线路所流过的零序电流幅值,而且相位也不再相反,因此很难根据各线路的零序电流幅值相位特征差异来选择故障线路[1]。
针对以上问题,本文采用信号注入法予以解决,并针对信号注入法本身存在的选线信号弱的固有缺陷,结合随机共振理论给予有效解决。
1 信号注入法
传统信号注入法的基本原理如图1所示,系统有三回出线。
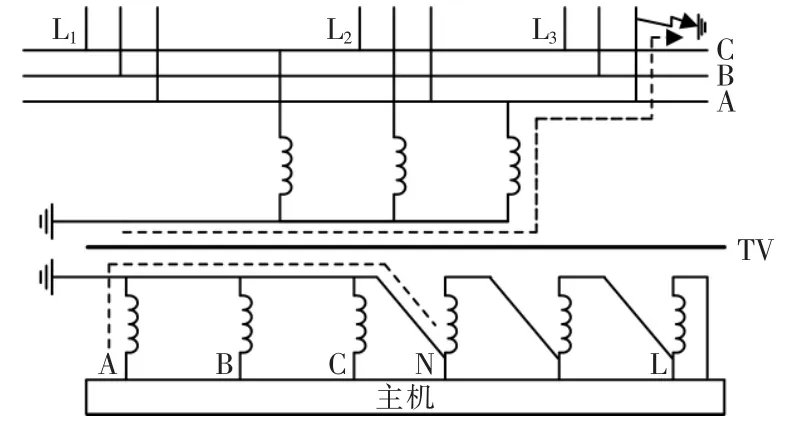
图1 信号注入法原理图Fig.1 Schematic diagram of the injection signal method
假设线路3 的A 相发生单相接地故障,系统A相的电压变为0,B、C 相的电压都升高为正常运行时的线电压,信号注入装置识别故障相后自动跨接在A、N 端子之间,将特定频率信号从电压互感器TV 二次侧的A 相注入配电网系统中。 信号电流将只在注入点和故障点之间流通,回路如图1中虚线所示,根据此特点,用信号检测装置对各条线路进行检测,能够探测到注入信号的线路即判定为发生故障的线路。
信号注入法实际应用效果不是十分理想,主要制约因素[2]有:①注入信号的能量受电压互感器TV容量的限制不能太大;②受接地过渡电阻较大或故障位置等因素的影响较大。 针对以上问题,本文采用随机共振理论使待检测信号幅值得到放大,从而检测出来进行选线。
2 变尺度随机共振的基本原理
2.1 随机共振理论
随机共振理论[3](stochastic resonance,SR)最早是由意大利学者Benzi 等人提出,主要描述在一个确定的非线性双稳系统中,单一的噪声或者微弱周期信号都不能使系统的输出从初始稳态发生跃变,而在两者共同作用下,调整噪声强度到匹配值时系统输出的功率谱中某一特定频率的周期信号的幅值将明显增大,此时部分能量从噪声转移到弱周期信号中,使待检测的微弱周期信号得到加强,更易于被检测到。
非线性双稳系统的动力学方程可以由Langevin方程来描述:

式中:V(x)为稳态势函数;A 为弱周期信号的幅值;ω 为弱周期信号的频率;n(t)为无规则的白噪声;n(t)满足下列条件:

式中:D 为噪声强度,双稳态势函数的数学表达式如下:

式中:a、b 均为大于0 的系统结构参数。
当n(t)=0 或没有周期信号输入时,若A<Ac,(Ac=代表双稳态系统的临界值),系统的质点将在势阱或内运动而不会发生跳跃;若A>Ac,系统的质点将克服势垒在势阱间作周期运动。 然而当噪声和微弱周期信号同时作用时,即使A<Ac,逐渐增加噪声强度D 到适当值,由于噪声和信号的协同作用,系统的势阱变得越来越倾斜,质点就能克服阻尼在势阱间发生跳跃,系统将不再稳定,从而使系统输出x(t)中微弱周期信号分量得到加强,这种状态就是随机共振。随机共振可以加强微弱周期信号的能量使之更容易被检测出来。
2.2 归一化尺度变换
上述随机共振由于绝热近似理论的限制,通常只能检测频率极低(ω<<1)的周期信号[4],为了满足实际工程应用的需要,通常进行尺度变换[5],令y=代入式(1)得:
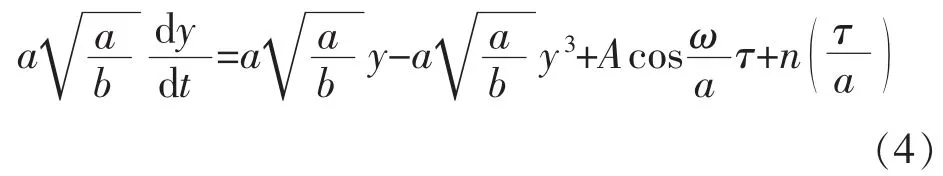
同理式(4)中噪声n(τ/a)满足:

将式(5)代入式(4)整理后得:

式(6)与式(1)等价,比较可知通过计算取合适的a 值即可将高频信号转化为系统要求的极低频;通过调整参数b 的值即可改变噪声强度以适应不同幅值的输入周期信号,从而使得工程实际中的高频信号也能应用于随机共振理论。
3 变尺度随机共振理论应用于信号注入法选线
注入信号的频率选定为f=225 Hz。 TV 二次侧所能注入的电流大小受其容量的限制,一般不超过10 A。当信噪比、系统参数及输入周期信号频率固定时,随机共振系统存在一个最佳匹配噪声值,使得该系统输出的信噪比增益最大[6]。 利用变尺度随机共振理论检测特定频率微弱注入周期信号的操作步骤如下:
(1)先用试验方法测得a=b=1、系统输入信号频率固定时,输入信噪比按照一定步长在一定范围内变化时,频率f0=0.1 Hz 所对应的最佳噪声方均根值δ0;
(2)用相关性粗劣估计实际频率为f=225 Hz 的待检测信号的噪声方均根值δ1;
(3)将相关数值及进行归一化反变换计算得出待检测信号信噪比与所对应的系统参数a,b 值。 并以信噪比增益最大为衡量指标,在估计值附近适当微调整得到适合实际信号检测的a,b 值;
(4)将a,b 值代入式(1),即得到对应于该输入信号的随机共振检测模型,根据模型输出判断输入信号中是否存在特征频率f=225 Hz 成分。
在用信号注入法选线时,故障线路输出的混合信号在频率f=225 Hz 处会出现一个明显的谱峰,表明系统已经达到随机共振,目标信号被明显放大;其余非故障线路由于没有注入的特定频率电流信号流过,因此系统不会出现随机共振。 两者相比较即可正确选线。
4 仿真验证
用Matlab 软件搭建系统仿真模型如图2所示。
仿真模型各元件参数如下:电源参数:出口电压10.5 kV,消弧线圈采用过补偿方式,补偿度取10%时,消弧线圈的电感L=7.4816 H;线路1~3 的长度依次为:15 km、20 km、16 km,有功负荷分别为1.3 MW、1.6 MW、2.0 MW。

图2 系统仿真模型Fig.2 System simulation model
线路正序参 数:R1=0.01273 Ω/km;L1=0.9337 mH/km;C1=0.01274 μF/km;零序参数:R0=0.3864 Ω/km;L0=4.1264 mH/km;C0=0.007751 μF/km。 线路3的A 相的10%处发生非金属性接地,设置接地电阻Rf=2000 Ω,故障发生时刻为0.04 s,故障发生后从母线电压互感器TV 二次侧注入频率f=225 Hz 及幅值为10 A 的正弦电流信号,然后从各线路距母线相同距离处所装设的信号探测装置中采集电流发送回主机进行处理。 首先通过带通滤波器将f=225 Hz的电流谐波分量滤出,从而得到理想条件下线路3的注入电流信号的波形图,如图3所示,线路1、2的注入电流信号几乎为零,可忽略不计。
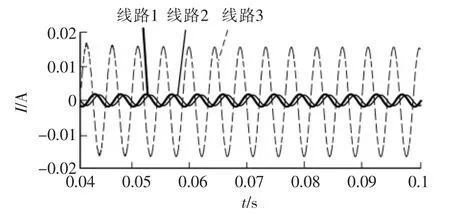
图3 各线路A 相注入电流波形Fig.3 Injecting current waveform of phase A of each line
将上述所过滤出的各注入电流信号分别加入噪声强度为D=0.2 的高斯白噪声后输入随机共振系统,图4(a)~图4(c)为各线路A 相混合输入信号频谱图。
采用参数调节SR 原理的微弱信号检测方法进行归一化尺度变换,设定参数a=2250,采样频率fs=45 kHz,估计待检测混合输入噪声信号的方均根值δ1为0.2024,在估计值附近计算并适当微调整随机共振系统中参数b 到合适值约为4.362×1012,使随机共振系统输出混合信号的信噪比增益达到最大,此时输出的混合信号在频率f=225 Hz 处会出现一个明显的谱峰,即随机共振状态。 此时各路信号的检测结果如图4(d)~(f)所示。 非故障线路1、2 的A 相输出信号频谱没有发生变化; 故障线路3 A 相注入信号幅值得到了有效放大,由原始的0.02 A 放大到了0.12 A 左右,选线准确率得到了极大提高。

图4 各线路故障相混合输入与输出信号频谱图Fig.4 Spectral diagram of mixed input and output signals of each line fault
为了验证所提选线算法的抗干扰性,仿真对可能影响选线结果的故障位置、故障相角、过渡电阻值及配电网拓扑结构等因素进行了试验,结果如表1所示。
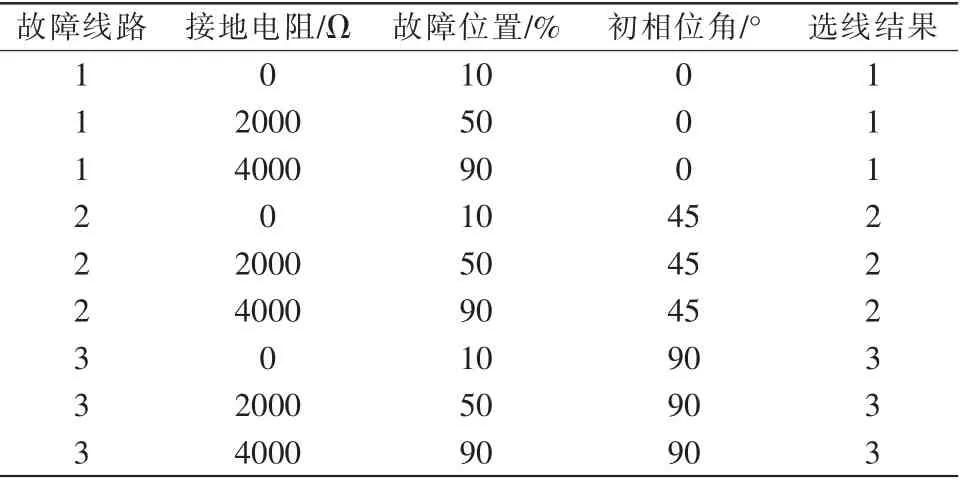
表1 不同故障条件下的选线结果Tab.1 Line selection results under different fault conditions
5 结语
本文采用变尺度随机共振理论,充分利用噪声来增强微弱信号能量,经过随机共振的故障线路和非故障线路的注入电流信号特征差异十分明显,使得传统注入信号法选线准确率得到了极大提高。
仿真中充分考虑了可能影响选线结果的各种因素,试验结果验证了所提选线方法的抗干扰性。本方法尤其适用于中性点经消弧线圈接地系统的故障选线。
实际工程应用中,可以在户外各测量点固定安装多组信号探测器来检测注入信号电流,可进一步实现故障点的自动区段定位。 该算法为小电流接地系统单相接地故障的高效选线定位提供了一种新的思路。
