镍基单晶高温合金孔洞缺陷数值模拟与控制方法研究进展*

刘可立，王俊升,，郭跃岭，杨彦红，周亦胄，杨院生

（1.北京理工大学材料学院, 北京 100081；2.北京理工大学前沿交叉科学研究院，北京 100081；3.中国科学院金属研究所高温合金研究部， 沈阳 110016）

镍基单晶高温合金是航空发动机涡轮叶片的关键材料，其组织完整性是影响涡轮叶片性能和服役寿命的重要因素[1–7]。孔洞作为一种微观组织缺陷，常常成为疲劳失效裂纹源[8–11]，是影响航空发动机涡轮叶片服役安全的隐患[11–16]。孔洞缺陷集中体现了镍基合金和涡轮叶片制造技术发展程度和服役性能优劣，始终贯穿于镍基单晶高温合金优化与代系更替发展历程中，而如何预测和控制孔洞缺陷始终是镍基单晶高温合金性能提升和工业化生产的重要难题。

本文针对航空发动机涡轮叶片镍基单晶高温合金凝固阶段、固溶阶段和服役阶段的不同孔洞缺陷，对国内外孔洞数值模拟方面研究现状及进展进行简要介绍，并对孔洞缺陷数值模拟发展方向进行展望。

铸态孔洞的数值模拟

1 铸态孔洞

铸态孔洞形成于合金凝固过程中，根据其形成机理主要可分为凝固缩孔和气孔两种。由于合金液相和固相密度不同，在凝固过程中产生枝晶间体积的收缩，如果收缩部分因枝晶臂阻隔而无法被合金液相补缩，则会产生具有复杂几何结构的凝固缩孔。铸态气孔则是由凝固初期合金液相中析出的气体聚集而成，不易受到枝晶结构的限制，因此气孔一般呈球形。由于镍基单晶高温合金冶炼质量及气体杂质的严格控制，铸态气孔的含量有限，因此目前镍基单晶高温合金的孔洞缺陷以凝固缩孔为主。根据Lee[12]和Stefanescu 等[17]对合金铸态缩孔模拟方法的分类和总结，可将凝固缩孔预测模型分为以下3种类型：基于试验数据的孔洞统计预测模型；合金凝固判据函数模型；耦合达西方程与质量、能量守恒定律的枝晶间液相流动模型。

2 基于统计学的孔洞模型

基于统计学的孔洞模型源自于孔洞表征的试验数据[18–20]。Zhang[21]和Zou 等[22]发现孔洞尺寸、数量和形貌与一次枝晶臂间距和二次枝晶臂间距密切相关。Liu 等[23]结合X 射线断层扫描（X–ray computed tomography，XCT）与凝固温度场有限元模拟，建立基于冷却速率的孔洞尺寸预测模型，并基于加热区温度、抽拉速率、炉体尺寸、激冷板温度和静置时间等参数的敏感性定量分析，建立工艺参数和孔洞尺寸之间的回归预测模型，通过优化工艺参数实现孔洞尺寸的调控与预测。基于统计学的孔洞预测模型可能对单一合金具有较好的预测效果，但无法广泛应用于具有不同化学成分的镍基单晶高温合金，应用范围较窄。

3 判据函数模型

判据函数孔洞模型主要考虑热传输对于孔洞的影响。Pellini 等[24]依据温度梯度和孔洞之间关系建立判据模型，认为完全凝固或凝固程度达到临界固相分数时，若局部区域热梯度小于临界值则产生缩孔，但该模型判定误差较大，且无法模拟出孔洞大小和含量。Sigworth 等[25]在Pellini 模型基础上，考虑镍基高温合金枝晶间通道补缩角对缩孔影响：

4 枝晶间液相流动计算模型

枝晶间液相流动计算模型耦合了枝晶间流体计算方程和能量、质量守恒方程，通过计算合金凝固过程中热传输和补缩压力降，实现凝固缩孔的预测。Walther 等[26]假设合金中液相流动通道近似为单个长管道，基于达西定律求解形成缩松所需的补缩压力值。Piwonka 和Felmings[27]在Walther 模型的基础上，将定向凝固铸件假设为多个管道密排系统，并引入曲折参数修饰枝晶间补缩通道的复杂几何结构，耦合基于质量守恒定律的连续方程与达西定律，利用环境压力和合金内局部压力之差计算产生缩孔所需的临界补缩压力：

式中，Pa为环境压力；Pm为合金内局部压力；μ 为合金流体黏度；β 为凝固收缩系数；c 为常数；L 为铸件长度；r 为组成铸件截面的近似管道半径；τ 为枝晶间管道的曲折参数；R为铸件截面近似半径；n 为组成铸件截面的近似管道数目。Piwonka 和Flemings 模型能够预测孔洞尺寸，但模拟得到的缩孔尺寸比试验结果较小。Lecomte-Beckers[28]基于枝晶间流体分析以及重力和合金元素对孔洞的影响，预测镍基合金形成缩孔所需的压力变化。Kubo 等[29]基于Piwonka 和Felming 的研究，假设孔洞成核于枝晶表面固液界面上，且孔洞受陷于二次枝晶，孔洞直径与二次枝晶臂间距相等，计算了液态金属补缩和孔洞变化体积，结果表明孔洞含量随冷却速率的增加而降低。Sabau等[30]在Kubo 模型[29]基础上，通过添加Forchheimer 项来描述枝晶间流体因流速过快而造成的动量损失，并基于固液相体积变化计算铸件内压力分布，再根据压力分布对合金中孔洞的分布进行预测。Poirier 等[31]则假设孔洞成核于一次枝晶臂间，并基于连续方程和达西定律，预测合金中孔洞含量。Felicelli 等[32]在Poirier的基础上，基于质量、动量、能量、元素扩散守恒方程，判断了镍基高温合金铸件内压力分布趋势、孔洞缺陷分布以及元素的偏析，分析了镍基合金中不同元素浓度对孔洞的影响。Gao 等[33]基于合金元素扩散建立了孔洞和元素偏析预测分析模型，并与Poirier 模型进行对比，预测孔洞含量在凝固后期会降低，并发现糊状区中的孔洞会降低枝晶间补缩速率以及溶质偏析。

Niyama 等[34]假设糊状区中流体运动满足达西定律，且凝固工艺参数决定糊状区中压力变化，并设定Niyama 参数（Ny）反映凝固后期铸件局部的凝固情况：

虽然Niyama 判据模型在部分镍基合金上有很好应用，但由于材料物性参数差异会导致形成缩孔临界Niyama 参数变化，因此Niyama 判据模型无法准确判定成分复杂镍基单晶高温合金缩孔形成倾向。梁作俭等[37]根据金属在凝固过程中液相收缩和在多孔介质中流体的模拟，建立了在离心压力条件下钛铝合金精密铸件微观孔洞模型。潘冬等[38]在Niyama 和梁作俭等的基础上，对宏观缩松采用Niyama 判据模型进行预测，对微观缩松使用梁作俭等提出的判据模型进行预测，建立了镍基高温合金熔模铸件凝固过程中缩孔的宏/微观多尺度模拟。

Niyama 模型对铸件局部补缩能力判断依赖于缩孔形成的临界Niyama 阈值。为了解决此问题，Carlson 等[39]建立了不借助临界值预测铸件中缩孔体积分数的无量纲Niyama 模型。无量纲Niyama 模型用达西定律表示枝晶间合金液相补缩压力的变化，并假设形成缩孔所需的临界压力为孔洞中压力与孔洞外部毛细压力之差：

式中，fl为液相体积分数；K 为糊状区渗透率。

为简化式（4），Carlson 和Beckermann 引用无量纲温度场对临界压力积分ΔPcr进行计算，并引入无量纲Niyama 参数Ny*，将压力积分调整为Niyama 判据方程的形式：

式中，λ2为二次枝晶间距。基于的计算，可推导当液态金属停止补缩时临界液相分数，进而预测铸件中不同区域孔洞体积分数。无量纲Niyama 判据模型弥补了Niyama 判据需要阈值进行求解的缺点，被运用于ProCAST 等软件，如图2 所示[39]。Khalajzadeh 等[40]在无量纲Niyama模型基础上，建立以孔洞为核心的计算模型，考虑了冷速、温度梯度和凝固收缩等因素对孔洞的影响。

图1 缩孔体积分数与Niyama判据之间关系Fig.1 Schematic of the relationship between volume fraction of shrinkage pores and Niyama criterion

图2 试验测量孔洞含量与Niyama参数分布和无量纲Niyama参数分布的比较Fig.2 Comparison between characterized shrinkage porosity and predictions from Niyama criterion and dimensionless Niyama criterion

表1 比较了3 种孔洞预测模型的差异。其中耦合了晶间流体分析解和连续质量守恒方程的孔洞预测模型可对镍基单晶高温合金中枝晶间压力变化进行描述，并预测孔洞在合金中分布和所占比例，现已逐渐替代孔洞判据函数模型。但目前枝晶间流动函数模型大多基于较为宏观的模拟计算，无法计算微观孔洞的尺寸和形貌等特征。

固溶孔洞的数值模拟

1 固溶孔洞

固溶处理是镍基单晶高温合金消除成分及组织不均匀性的重要方法，但也是影响孔洞形成的重要因素。Anton 等[41]分析了镍基单晶高温合金固溶微孔的4 种形成原因：析出气体聚集而产生的气孔；氧与碳或含碳析出相反应而在晶界处生成的气孔；固溶相变体积变化所造成的空位；固溶过程中枝晶干与枝晶间富集元素因扩散速率不同而产生的空位聚集（Kirkendall 效应）。

但在镍基单晶高温合金固溶处理过程中，溶解气体被严格控制，合金中Cr 和Al 等元素比碳容易形成氧化物，难以形成固溶气孔；且γ 相晶格尺寸大于γ'相晶格尺寸，也难以因不同相之间的体积变化而形成空位聚集的情况，因此由Kirkendall效应而产生的空位聚集是形成镍基单晶高温合金固溶孔洞的主要原因。石倩颖等[42]基于铸态微孔和固溶后微孔的量化表征和研究，也验证了Kirkendall 效应为形成固溶微孔的主要原因。

2 固溶孔洞的预测模型

图3 二元相场晶体模型对晶界附近Kirkendall孔洞演化过程的模拟Fig.3 Simulation of Kirkendall pores by binary phase–field crystal model

最初预测固溶孔洞演化行为模型主要基于试验观测铸态孔洞在固溶过程中变化规律。Chaijaruwanich等[43]结合XCT 研究了合金在固溶过程中孔洞的尺寸、几何形貌和含量变化，并使用一维有限差分算法来计算固溶过程中空穴的扩散和聚集，结果发现孔洞缺陷在固溶过程中因奥斯瓦尔德熟化效应，孔洞尺寸在固溶过程中增大，且尺寸较小孔洞在固溶过程中聚集，形成了较大孔洞。Bokstein 等[44]针对镍基单晶高温合金建立了基于枝晶附近元素扩散解析模型，计算了枝晶周围元素随时间变化配分系数，以及固溶孔洞的体积变化，通过模型发现合金元素偏析程度、扩散系数和枝晶间距对固溶孔洞生长具有重要影响。借助蒙特卡洛法和分子动力学计算方法，Belova[45]和Evteev 等[46]对中空纳米晶的Kirkendall 效应进行了模拟，但没有考虑合金中晶体和晶界特征对Kirkendall 孔洞的影响。近年来借助相场和元胞自动机等模拟方法，中外学者对合金中Kirkendall 孔洞形成和演化机理有了更深入理解。Elder等[47]使用二元合金相场晶体模型在原子尺度上模拟了元素在扩散过程中浓度变化和空穴的演化行为，揭示了Kirkendall 孔洞演化机理，并得出晶界上容易形成Kirkendall 孔洞的结论。Lu 等[48]在Elder 等[47]的相场晶体模型基础上，假设晶格参数和元素浓度场呈线性相关，修改了自由能计算公式，对晶界上Kirkendall 孔洞的形成和演化行为进行模拟，模拟结果与观察到的镍基合金固溶孔洞演化行为具有较好的一致性，如图3 所示[48]。该模型较好地验证了Kirkendall 效应可以导致晶界上形成孔洞的现象，并发现晶界角度会影响固溶孔洞距离晶界的位置与分布。

服役中孔洞数值模拟

1 服役孔洞

微观孔洞作为蠕变及疲劳失效的裂纹源，会引起镍基单晶合金高温力学性能锐减，从而有可能导致叶片失效断裂，成为重大安全事故的隐患。镍基单晶高温合金的服役性能主要受两种孔洞缺陷的影响：蠕变孔洞和铸态孔洞。镍基单晶高温合金中的蠕变孔洞主要由攀爬在垂直于受力载荷γ/γ'相界面位错滑移所引起空位富集而产生[49–51]。蠕变孔洞长大机理主要有3 种：空位扩散主导的蠕变孔洞长大机理；蠕变孔洞周围金属塑性变形所主导的孔洞长大机理；因补偿外载荷所造成应变而促使蠕变孔洞长大的机理[52]。镍基单晶高温合金蠕变孔洞尺寸一般小于合金在凝固过程中产生的铸态孔洞，并且蠕变孔洞与铸态孔洞关系紧密[4，53–54]，因此，研究铸态孔洞在服役过程中的演化机理对提高镍基单晶高温合金涡轮叶片服役寿命同样有着重要意义。

2 服役孔洞的预测模型

蠕变孔洞预测模型的构建主要依赖于蠕变孔洞的形成和长大机理。Hull 等[55]基于蠕变孔洞由空穴扩散控制的假设，根据晶界处空位化学势梯度计算空位扩散速率，并分析应力对蠕变孔洞的影响。Hayhurst[56]基于金属塑性变形所主导蠕变孔洞长大机理，建立受应力控制的蠕变孔洞长大解析模型，并被运用到法国核装置机械部件设计和建造准则（RCC–MR）。Spindler 等[57]基于空位扩散和应变控制孔洞长大机理，建立孔洞扩散和长大主导多轴应力状态下蠕变断裂预测模型。Dyson 等[49]基于合金内部位错运动不稳定性和蠕变孔洞的损伤，开发了镍基高温合金蠕变连续损伤模型，发现蠕变孔洞在低延展性合金蠕变损伤中起主导性作用。

传统蠕变孔洞长大理论解和解析解难以描述复杂几何结构和载荷形式下镍基单晶高温合金构件蠕变损伤机理，而有限元数值模拟方法为深入研究镍基单晶高温合金蠕变孔洞损伤行为提供了便利条件。Sirvastava 等[58]基于三维有限元单胞模型，对不同应力下镍基单晶高温合金蠕变孔洞的演化行为进行分析，发现只有间距足够近的孔洞会在蠕变过程中聚合和长大，如果间距太大，蠕变孔洞会塌陷。Yu 等[59]基于晶体塑性理论和非线性刚度法，利用三维有限元模型系统分析了应力三维度、孔洞初始体积分数、Lode 参数、晶体取向、滑移系统激活能和弹性各向异性对蠕变孔洞生长的影响，发现在高应力三维度下蠕变孔洞体积膨胀，而在低应力三维度下蠕变孔洞形状具有明显变化；Lode 参数对孔洞长大和形貌有明显作用；晶体取向能影响蠕变孔洞长大方向及蠕变裂纹扩展方式。张姝等[60]基于有限元模型，对镍基单晶高温合金在高温蠕变期间有蠕变孔洞和无蠕变孔洞的区域进行分析，发现有孔洞区域两侧极点具有较大应力，说明蠕变孔洞缺陷能降低合金寿命。

近年来，得益于相场模拟方法技术发展，Yang 等[61]将涉及微观蠕变孔洞形成因素的Kachanov’s 蠕变损伤定律、晶体塑性模型与相场法相结合，模拟了γ/γ'相蠕变演化过程，揭示了γ'颗粒在蠕变过程中形貌演化机理。结合了相场法、有限元等数值模拟方法多尺度蠕变孔洞缺陷模型，有望揭示镍基单晶高温合金蠕变孔洞缺陷形成和演化机理。

相关研究表明[1，3–4]，铸态孔洞是影响镍基单晶高温合金疲劳性能的重要因素。Paris 方程[62]因描述了裂纹扩散速率和应力强度参数之间关系而被广泛应用，该模型预测了合金内部由孔洞等缺陷产生的微小裂纹从亚临界尺寸生长到临界尺寸过程中所需循环次数。随着对孔洞缺陷更深入了解，国内外学者发现孔洞含量、尺寸、形貌、距合金表面距离、相邻孔洞间距和孔洞与其他微观结构之间相互作用对疲劳性能都有较大影响[63–67]。为揭示孔洞缺陷疲劳损伤机理，Fan 等[68]率先通过有限元模拟研究合金内部铸态孔洞的大小、间距、长径比和聚集度等因素对合金疲劳性能影响，发现对低孔洞含量合金，微观尺度上循环塑性与合金疲劳强度有较好的对应关系，因此可以基于孔洞和夹杂颗粒的有限元模拟建立合金疲劳裂纹萌生模型。Bourbita 等[69]基于有限元和晶体黏塑性本构方程，计算了镍基单晶高温合金构件中预制缺口区域在高温低周疲劳载荷下的应变梯度，并针对铸态孔洞缺陷形成微小裂纹演化行为进行模拟和试验比较，获得了由合金内部缺陷演化为损害合金疲劳寿命的裂纹萌生周期预测模型。

X 射线表征技术快速发展为揭示合金中孔洞缺陷形成、演化和疲劳损伤机理创造条件[70–73]。Li 等[74]将XCT、准原位疲劳试验和有限元疲劳损伤模拟结合起来，研究了孔洞分布对合金疲劳裂纹影响，对孔洞缺陷多尺度、全流程控制策略具有指导意义。Dezecot 等[75]基于X 射线同步辐射技术和有限元模拟方法，分析了合金中铸态孔洞对低周疲劳裂纹的影响，研究表明孔洞附近存在较大应力和非塑性应变区域，这些区域与疲劳裂纹的萌生和扩展方向密切相关，如图4 所示[75]。Prithivirajan 等[76]以晶体塑性模拟和有限元模拟为基础，结合XCT 表征技术，分析了关键孔洞缺陷对IN718 镍基合金疲劳性能的影响，并使用非局部疲劳损伤参数识别疲劳裂纹萌生位置（图5），这种耦合晶体塑性和有限元分析的研究方法在揭示关键孔洞尺寸的影响方面具有重要的参考价值。

孔洞的检测和模拟验证

要揭示孔洞的损伤机理，掌握孔洞控制技术，则必须要对孔洞缺陷的形成和演化行为进行观察，为建立孔洞预测模型提供试验支撑。

微观孔洞的传统表征技术主要是利用光学显微镜、扫描电子显微镜等检测设备，对金相截面进行观察分析，并利用图像处理软件对微孔特征进行分析。Gao 等[77]通过光学显微表征，量化分析了孔洞尺寸和距合金表面距离对铸件疲劳寿命的影响，并基于电子显微镜所提取的孔洞微观特征形貌，建立了描述孔洞缺陷引发裂纹萌生的有限元模型以及孔洞尺寸–应力–疲劳寿命预测模型，预测结果与试验数据吻合良好。Brundidge 等[78]基于光学表征将不同尺寸的孔洞分布映射到枝晶核排列的维诺图中，建立了基于枝晶间渗透率、液相分数及枝晶间距的最大孔洞尺寸预测模型。

镍基单晶高温合金中的铸态孔洞缺陷大多是因枝晶间通道内补缩不足所造成的凝固缩孔，因此镍基单晶高温合金中的铸态微孔具有较为狭长、形貌复杂的几何特点。传统表征手段可以获取微孔的二维平面信息，但无法观测和提取微孔的真实三维形貌及分布特征。利用X 射线的穿透性，人们可以较准确地分辨出合金中具有不同密度的区域，并提取合金中孔洞缺陷的三维几何结构。Link 等[71]通过XCT 技术对镍基单晶高温合金孔洞的三维形状进行了研究，并据此建立了孔洞缺陷的三维形状因子评估模型。

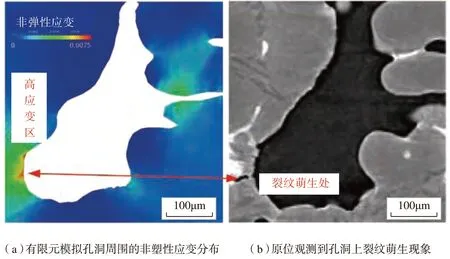
图4 有限元模拟孔洞周围的非塑性应变分布与原位观测到孔洞上裂纹萌生现象的对比Fig.4 Comparison between finite element simulation of inelastic strain around a pore and tomographic slice showing crack initiation from pore

此外，传统表征手段一般具有破坏性，无法对孔洞的形成和演化行为进行观察，具有较大的局限性。因此，三维跨尺度直接观察微孔的产生及演变，对于深入研究微孔的形成机理至关重要。借助X 射线成像技术，Lee 等[70]率先基于定向凝固实验台和X 射线成像技术，对铝合金中孔洞缺陷的形成和演化过程进行了原位观测，通过试验可以量化形成合金中氢过饱和度、抽拉速率、温度梯度和合金组成对孔洞演化的影响。基于原位观察的结果，Atwood 等[79]借助元胞自动机–有限差分法建立了模拟孔洞的形成和演化预测模型，能较准确预测铝合金中气孔的大小、形貌和分布情况。

随着X 射线成像技术的发展，同步辐射技术能够提供更强穿透力、更稳定的X 射线光源，为研究镍基合金孔洞缺陷演化行为的原位观察创造了条件。借助同步光源，Plancher[72]和Chauvet 等[80]发现镍基合金在凝固初期会因沿垂直一次枝晶臂方向补缩不足和二次枝晶粗化导致枝晶臂聚结而引起的小尺寸凝固缩孔，这种缩孔虽然尺寸较小，但沿凝固方向规则排列，对镍基合金的疲劳损伤研究具有重要意义。

图5 基于有限元建立晶体塑性本构模型对镍基合金孔洞缺陷研究Fig.5 Sequence of steps followed in critical porosity using CP–FE simulations

随着X 射线成像技术的进步，对轻质合金中孔洞缺陷形成和演化行为的原位观察试验技术已较为成熟。但对于高原子序数镍基单晶高温合金凝固、固溶和服役条件下孔洞缺陷的原位观测目前仍难以实现。

孔洞缺陷的控制方法

为了提高航空发动机服役性能，延长航空发动机的使用寿命，镍基单晶高温合金孔洞缺陷的控制技术尤为重要。镍基单晶高温合金的铸造工艺对合金内铸态孔洞有着显著的影响，其中抽拉速率、温度梯度和合金成分对铸态孔洞的影响最大。抽拉速率过慢或过快都会使镍基单晶高温合金中铸态孔洞缺陷的情况更加严重。Atwoo 等[79]基于铝合金的孔洞预测模型研究了定向凝固条件下抽拉速率对孔洞形成和演化的影响，指出低抽拉速率条件下易形成少量尺寸较大的孔洞，而高抽拉速度下会形成大量尺寸较小的孔洞。Whitesell 等[81]基于试验，同样发现了抽拉速率对Mar–M247 合金具有相似的影响：发现当抽拉速率小于0.005cm/s 时，会产生枝晶向胞状晶的转变，虽然较大孔洞的尺寸会减小但孔洞数量会增多，使合金的整体缩孔情况更加严重；当抽拉速率大于0.01cm/s 时，过快的抽拉速率对导致凝固前沿热流的不稳定，容易造成凝固方向与抽拉方向的偏离，导致局部凝固的不均匀，使合金内的孔洞缺陷更加严重。

在镍基单晶高温合金的定向凝固过程中，更高的温度梯度能抑制合金中铸态孔洞的形成。液态金属冷却法(Liquid metal cooling，LMC)在高速凝固法的基础上，在冷却区添加液态金属作为传热介质，使合金的冷却方式从辐射换热改进到传导换热，极大增加了散热效率，使合金凝固前沿的温度梯度得到进一步提高。Brundidge 等[78]比较了传统单晶铸造Bridgman 法和LMC 法两种工艺所制备的RENE N5 合金中孔洞缺陷，发现LMC 技术能够使孔洞缺陷的最大尺寸减小65%，并基于凝固过程中枝晶间渗透率、液相分数及枝晶臂间距建立了简单的最大孔洞缺陷尺寸的预测模型。

除了改进凝固工艺外，合金成分调整也是控制镍基单晶高温合金的孔洞缺陷的途径，其本质在于对凝固温度区间、合金共晶含量和微观元素偏析等凝固特征的调控。Lecomte–Beckers[28]基于孔洞预测模型和试验验证的方法，认为Al 和Ti 会扩大凝固温度区间，Co 促使枝晶间通道形成更加复杂的结构，而Cr 会降低合金固相和液相之间的密度差。因此Al、Ti 和Co 会促进合金中孔洞的形成，而Cr 会抑制孔洞的形成。此外Lecomte–Beckers 还认为Mo 和C 对调控镍基合金中的孔洞缺陷具有二重性：Mo 的添加可能会通过提高凝固速率来促进孔洞的生成，或通过降低固相和液相的密度差来抑制孔洞的生成；C 的添加可能会通过扩大凝固温度区间来促进孔洞的生成，或通过降低枝晶间补缩通道的复杂性来抑制孔洞的生成。但目前关于C 元素对镍基单晶高温合金孔洞形成倾向的影响机制仍存在争议。Chen等[82]认为C 的添加会促进MC 碳化物的形成，MC 碳化物不仅因为尺寸较小而不易降低液态合金的流动性，而且会在凝固后期因晶格膨胀而补偿缩松，达到抑制孔洞缺陷形成的作用。Al–Jarba 等[83–84]则认为C 的添加会促进C 网络的形成，而C 网络会扰乱液相的流动，扩大糊状区上下区域的密度差，会明显增大孔洞尺寸的含量和减小孔洞缺陷的尺寸。

虽然通过调整工艺参数、合金元素可以达到一定程度上控制镍基单晶高温合金铸态孔洞缺陷的效果，但由于镍基单晶高温合金制备工艺复杂，合金元素繁多，铸造、固溶处理和服役过程中均难以完全避免孔洞缺陷的产生。热等静压（Hot isostatic pressing，HIP）作为一种利用高温高压的封闭环境对合金材料进行压制以优化微观组织的后处理技术，能够显著减少合金内的多种孔洞缺陷，被广泛应用于航空领域。Wasielewski等[85]认为热等静压技术消除孔洞缺陷的过程是一个蠕变和扩散相结合的过程，首先应力引起孔洞的蠕变闭合，同时孔洞表面相互接触并发生扩散结合，从而减少孔洞缺陷。

基于镍基单晶高温合金铸件结构的特殊性和重要性，人们对镍基单晶高温合金的性能要求日益苛刻。孔洞缺陷作为一种单晶高温合金中的常见缺陷，严重降低了铸件性能，成为服役过程中的安全隐患。目前能有效减少单晶高温合金中孔洞缺陷的主要方法还是基于铸造工艺的调控。但由于镍基单晶高温合金成分复杂，影响因素较多，只有完全掌握合金中孔洞缺陷的形成和演化机理才能更有针对性地控制孔洞缺陷[86]。

结论

近年来，国内外镍基单晶高温合金孔洞成核和演化多尺度表征与数值模拟研究进展显著，但模型仍存在使用理论分析、经验函数方程来简化物理现象，在揭示孔洞演化机理和控制孔洞方面仍存在一些不足：

（1）针对凝固缩孔数值模拟仍停留在宏观尺度，常用的缩孔判据模型无法预测孔洞的尺寸和形貌等微观特征；

（2）针对高温合金的介观和微观组织模拟大多将其简化为二元合金，难以反映不同合金元素对凝固缩孔和固溶微孔的影响规律和作用机理；

（3）常规缺陷模拟主要针对单一缺陷，尚未建立孔洞与枝晶、碳化物等其他微观组织结构在凝固、固溶和服役过程中的多种缺陷相互作用模型；

（4）镍基单晶高温合金孔洞缺陷的控制仍依赖于制备工艺的改进，以试验为基础研究孔洞缺陷形成机理的局限性逐渐凸显，并且缺乏能够精确指导制备技术优化的孔洞预测模型。

随着计算技术的发展，越来越复杂的数值模拟计算可以被实现。基于多相多参量的微观孔洞预测模型因其能揭示镍基单晶高温合金中孔洞缺陷的形成和演化机理，是将来孔洞预测模型的发展趋势。近年来基于GPU 并行计算的加速算法方法因其算法实现简单、加速效果好的优点而被广泛应用于数值模拟领域，有望被应用到镍基单晶高温合金孔洞缺陷预测模型中。

未来孔洞缺陷方面的研究将跨尺度三维原位表征技术和多尺度、多相和多参量数值模拟方法相结合，必将会从深层次揭示“工艺参数–微观组织–材料性能”之间内在关系，镍基单晶高温合金铸造和固溶处理工艺的数字化调控以及服役性能的高精度预测，有望成为新的发展方向。