水化—热耦合模型预测防辐射混凝土早期温度场变化★

2020-11-03刘洋洋吴世通连春明

山西建筑 2020年21期

刘洋洋吴世通王进连春明

(中国建筑第八工程局有限公司,上海 200122)

1 概述

防辐射混凝土对混凝土密度、结晶水含量、裂缝控制等有很高的要求，防辐射混凝土配合比会依要求一定量的特殊骨料，如蛇纹石、重晶石等[1-4]。某医院项目采用大体积重晶石混凝土对直线加速区进行辐射屏蔽，其密度和热工性能均需依实际情况进行考虑。大体积防辐射混凝土裂缝控制对温度控制有较高的要求[5-7]，现有标准对混凝土早期放热的计算没有考虑混凝土水化速率的非线性变化和温度对其的影响[8]。

对混凝土水化模型的研究一直是学界和工业界的热点，但是由于混凝土胶凝材料组分的多样性和性能的不稳定性，仅通过查表等方式难以获得准确描述某一实际工程所用材料的水化模型参数。对胶凝材料组分进行分析可以得到其矿物组成，通过对各成分的水化过程进行叠加可以得到胶凝材料整体的水化放热规律[9]，但进行化学成分分析、粒径分析等试验须使用专用的分析设备进行较长时间的测试。工程的进度、现场实验室配置等因素制约了使用这种方法对胶凝材料水化过程进行预测。因此，对于实际工程应用而言，有必要探索一种简易、使用且准确的预测水化热的方法，这种方法既需要能够准确地反映出不同温度变化过程对混凝土水化的影响，也要在工程上让技术人员能够简单掌握并进行相关试验。

2 材料与实验

2.1 材料

水泥采用P.O42.5级水泥，初凝158 min，终凝207 min，标准稠度用水量27%，3 d，28 d抗压强度分别为29.8 MPa和49.2 MPa。

粉煤灰采用Ⅱ级粉煤灰，45 μm方孔筛余19.9%，需水量比101%，烧失量6.4%，活性指数77%。

粒化高炉矿渣粉采用S95级矿粉，7 d，28 d活性指数分别为74%和98%，流动度比105%，烧失量0.8%。

粗集料采用福建产重晶石，表观密度4 250 kg/m3,堆积密度2 470，最大粒径31.5 mm。

细集料采用与粗集料同产地重晶石与开化产机制砂混合，重晶石砂表观密度4 250 kg/m3，开化产机制砂表观密度2 640 kg/m3，混合后符合Ⅱ区中砂要求，细度模数为3.0。

减水剂采用聚羧酸减水剂，密度1.029 g/cm3,pH值6.8，净浆流动度185 mm，减水率21.1%。

拌和用水采用符合JGJ 63—2006混凝土用水标准的地下水。

膨胀剂采用HEA型复合膨胀剂，符合标准GB 23439—2017混凝土膨胀剂。

底板强度等级为C35，通过试配最终确定防辐射大体积混凝土配合比见表1。

表1 底板混凝土配合比 kg/m3

2.2 实验方法

因为本次研究的混凝土胶凝材料种类较多，且在工期压力下，短时间内成分难以确定，所以采用测量隔热条件下的混凝土温度变化曲线来对混凝土水化模型和传热模型参数进行拟合。为了直观地评价通过水化模型、传输模型以及简化的混凝土隔热温升的试验对混凝土浇筑早期温度变化预测的可行性及准确性，在浇筑时期通过光纤温度传感器监测了混凝土底板某些区域的温度变化，通过监测值和计算值的比较来评价实验方法和数值模型的准确性。

2.2.1绝热温升

在本研究进行的绝热温升实验中，将新拌混凝土装入聚苯乙烯保温箱中(保温箱外尺寸为290 mm×370 mm×250 mm；保温箱内尺寸即混凝土试样的尺寸为250 mm×320 mm×200 mm)，谨慎插捣后，将热电偶温度传感器埋入混凝土中。用玻璃胶带将保温箱缠紧并覆盖拼缝，见图1。

在距保温箱约20 cm处设一测点测量环境温度。将传感器连接至温度记录仪(深华轩科技有限公司MT-X型)进行记录，热电偶测量精度为±0.5 ℃，记录分辨率为0.1 ℃。连续记录5 d的温度数据，数据记录间隔为10 min，见图2。

2.2.2底板温度监测

基础材料为钢筋混凝土，大部分区域厚度1 000 mm，板底结构标高-5.6 m，整体模型见图3。

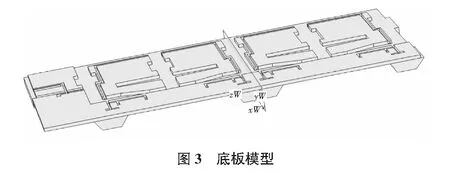
测点设在底板中部，沿竖直方向布置3个传感器，分别为距离顶面20 cm，距顶面50 cm和距底面5 cm，示意图见图4。

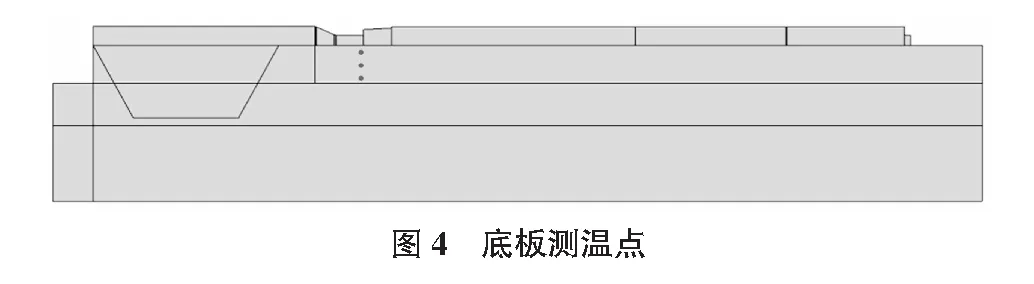
底板温度监测采用上海派溯KNPGT-1型埋入式光纤传感器，经调制解调器处理信号后将监测数据发送至云平台存储。测量精度为±1 ℃，分辨率为0.1 ℃，监测时长2周，读取数据间隔约为2 min。

3 混凝土浇筑早期的温度场变化仿真

3.1 传热过程控制方程和胶凝材料水化模型

混凝土内部水分传输在传热过程对温度的影响可以忽略，热传导遵循傅里叶定律，写作：

(1)

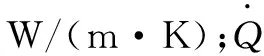
胶凝材料的水化采用基于水化度的模型，定义水化度为胶凝材料在水化过程中释放的热量与其完全水化后产生的总水化热的比值[10]：

(2)

其中,Qpot为胶凝材料完全水化产生的水化热,kJ/kg。

在20 ℃的标准养护条件下，胶凝材料的水化速率按式(3)计算[11]。

(3)

其中,ATref为在参考温度下的水化速率,s-1；g(T)为温度对水化速率的影响系数，分别由式(4)和式(5)来计算：

(4)

(5)

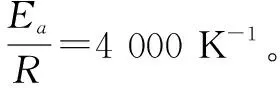
因为式(4)中参数B2对水化速率影响不大，所以本研究中对式(4)进行简化，得到：

(6)

αmax为胶凝材料能达到的最大水化度，通过式(7)计算[12]。

(7)

3.2 边界条件

混凝土传热的边界条件为第三类边界条件，即热流密度与边界处换热系数和环境温差相关，写作：

-n·q=Heq,i(Text-T)

(8)

其中，q为边界热流密度,W/m2；Heq,i为边界i的等效换热系数,W/(m2·K)；Text为环境温度,K。

Heq,i可以由式(9)计算。

(9)

其中，Hair为空气对流换热系数,W/(m2·K)，由式(10)计算得出[13]，其中Sw为风速,m/s；a和b均为拟合系数；Hrad为辐射等效换热系数,W/(m2·K)；ef,ij为边界i上第j层保温层厚度，m；λf,ij为其导热系数,W/(m·K)。

(10)

3.3 绝热温升试验的仿真及水化模型参数的确定

绝热温升试验仿真计算的简化几何模型及其网格划分如图5所示，外层保温材料和混凝土试样尺寸与实验中数据一致，因对称性建立1/4模型，网格以四面体单元划分，共170 000个单元，最大单元尺寸为26 mm。

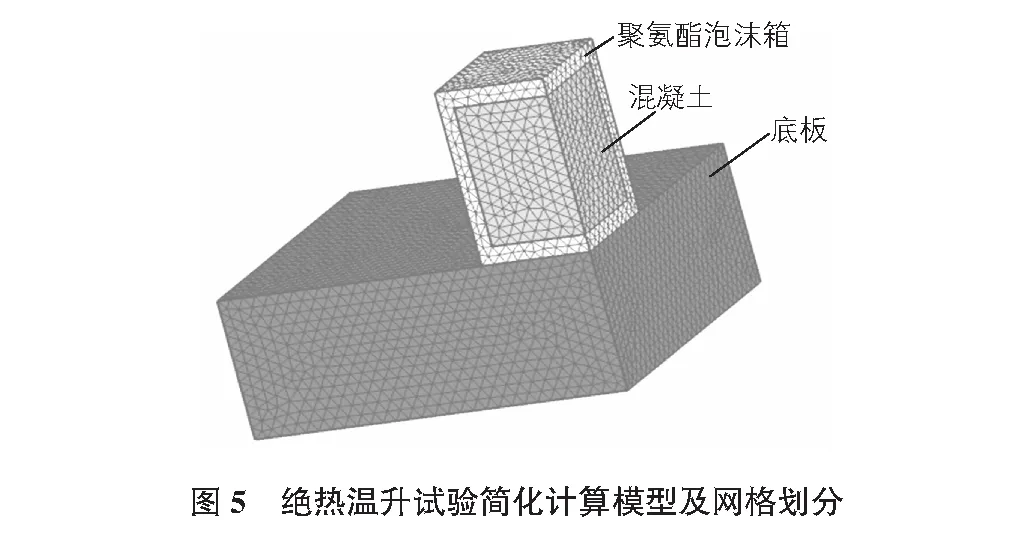
计算所用参数见表2。

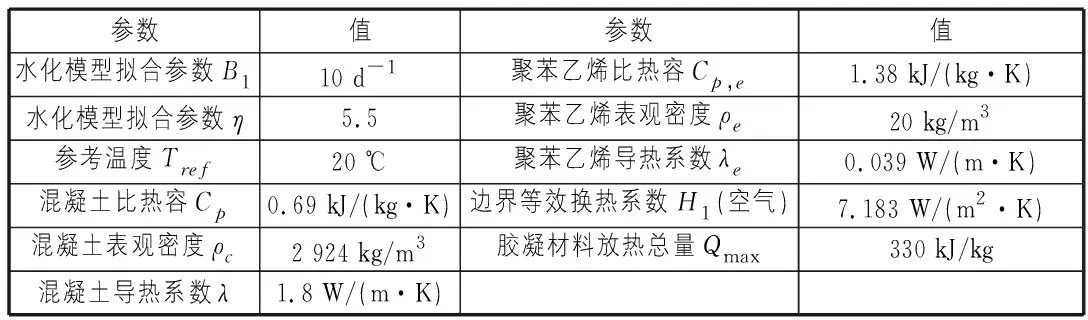
表2 绝热温升试验仿真所用参数

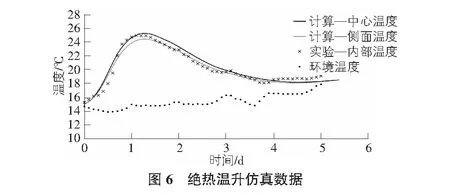
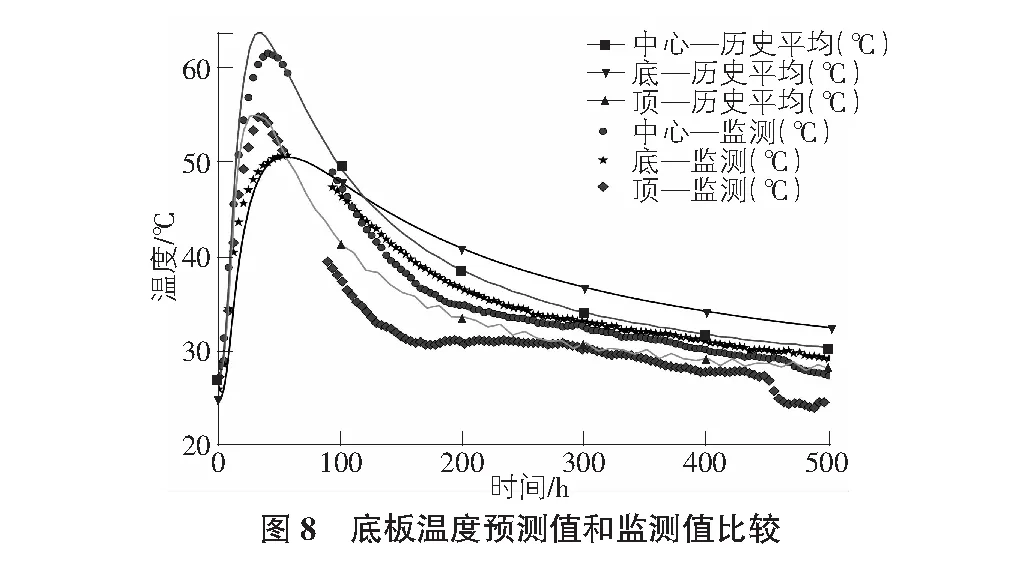
其中水化模型的参数B1,B2和η文献[11]所述范围内进行微调，以尽量使监测值位于计算所得混凝土中心温度曲线和距保温箱相邻侧面各1 cm处(侧面温度)温度曲线之间。边界条件中的环境温度使用环境监测数据，计算所得的混凝土中心温度和侧面温度随时间变化曲线见图6，可见计算温度与实测温度时变规律相同，结果相近。因此，表2中的参数可用于底板温度预测的仿真计算之中。

3.4 底板早期温度变化仿真

3.4.1模型简化及网格划分

根据对称性将图3中底板的一半进行分析，如图7所示，底板为表1中所述混凝土，地基材料为土，厚度约3 m。

同样采取自由四面体网格对模型进行网格划分，共计210 000个体单元，最大单元尺寸为1.48 m。

3.4.2环境边界条件

根据进度计划，9月下旬进行直线加速器区底板浇筑，根据天气数据网站结果，上年度当地9月日均最低温度为21 ℃，最高为29 ℃，风速约为8 m/s，以此作为边界条件的依据进行仿真计算，即边界温度为25 ℃+4sin(2π(t-0.25d))。

与绝热温升试验使用参数不同之处在于边界条件以及增加了地基的材料，涉及参数见表3。

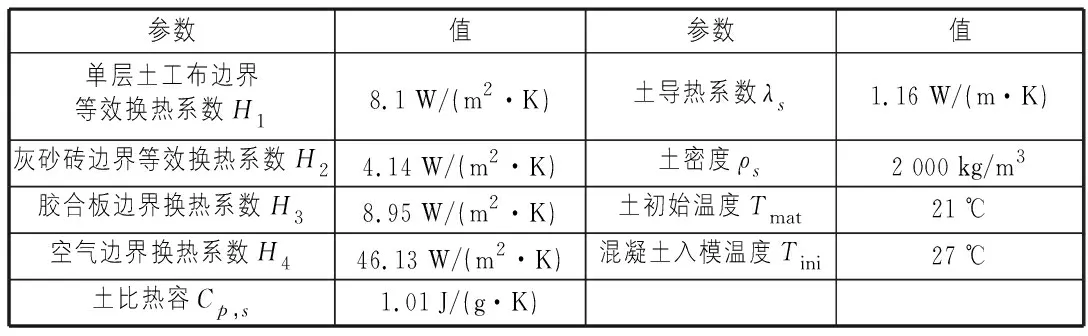
表3 底板仿真所用参数

底板浇筑及随后养护的过程中，顶面覆盖5 mm厚的土工布，外围用灰砂砖砌筑模板，内测垂直于地面的边界为15 mm厚木胶合板，底板外为空气边界。将仿真计算得到的各测点温度随时间变化(记作“—历史平均”)与现场监测数据(记作“—监测”)进行比较，结果见图8，由于现场供电问题，在浇筑后60 h～90 h期间监测数据中断，但不影响其他监测时间的数据。可以看出，通过简单的实验室绝热温升试验修正参数得到的水化模型可以较为准确地预测出各点达到最高温度的时间和前期放热情况。从浇筑开始计时500 h以内，底部、中心和顶部测点监测值的最高温度分别为50.7 ℃，61.5 ℃和55.0 ℃，而仿真计算得到的同样位置的最高温度分别为50.5 ℃，63.7 ℃和54.9 ℃。可以看出，中部和监测结果差距最大，比监测结果高出2.2 ℃，而顶部和底部的计算结果与监测值差距仅为0.2 ℃左右。仿真结果中各点温度达到峰值的时间略早于监测数据，但整体结果依然较为准确，在100 h后仿真结果温度比实际监测温度高，这可能是由于浇筑72 h后将底板表层土工布移除，改为洒水养护导致表面传热系数迅速增加造成温度骤降，见图9。由于本研究中模型未设计降雨导致的传热变化，因此与监测值之间有着一定的偏离。

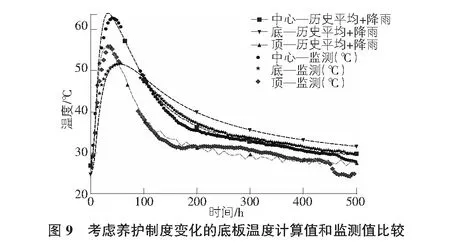
若将改变养护措施对底板表面造成的影响考虑其中，假设洒水养护混凝土表面换热系数等于无覆盖养护，即上表面等效换热系数由式(11)表示，得到结果见:

(11)

可见，各点温度随时间的变化曲线更接近监测值，底层计算和监测温度在72 h之后与监测值之差较顶层和中部稍大，这和底板与地基的实际连接复杂程度和模型之间的差距有关。实际底板与地基之间还有防水层和垫层，并且地基土体热工性能为估算值，也是误差的来源。但总体上能够反映底板混凝土早期温度变化的过程，并且在前100 h时能够对实际温度变化进行准确地预测。

因为实际气温和上述仿真计算中的取值有一定的差距，为了解温度边界条件对仿真计算结果的影响，比较了以记录温度作为边界条件和以往年气温平均值作为边界条件的仿真结果。

根据当地地区气温记录，将每日最高/最低气温记录作为当日14时和次日2时的气温，气温随时间变化曲线的其他部分通过三次多项式插值方法获取，并与计算时所用环境温度数据(往年气温均值)同绘于图10。

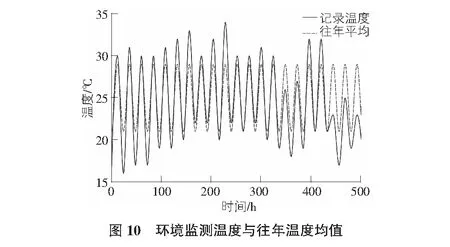
可以看出，在计算的时间内，记录的气温整体上处于先升温、后降温的过程，期间存在不规律的波动。在浇筑完毕后的150 h内，记录气温的当日最高/最低气温比模型中使用的平均气温值高/低，之后基本与估计温度一致，在300 h～400 h,440 h～500 h时间段有明显降温，计算结果比较见图11。可以看出，依记录气温计算出结果和依历史平均值计算出的结果相差不大，甚至在100 h～200 h区间内与监测值差距更大。依气温记录计算的结果能够反映出气温的骤升/骤降，如460 h～500 h区间内的计算结果能够明显看出温度降低。

气温记录本应更加接近监测数据，但是计算结果在某些区域(如100 h～200 h段)与监测数据差距反而更大，这可能是因为计算中使用的等效换热系数的误差大于温度的差异，土工布受潮、局部区域覆盖不严、短时大风、降雨、太阳辐照等均会影响实际边界温度的变化。尽管如此，仿真结果与监测值的差距依然在可以接受的范围内。