区块链赋能的边缘异构计算系统中资源调度研究

张平，李世林，刘宜明，秦晓琦，许晓东

（1.北京邮电大学网络与交换技术国家重点实验室，北京 100876；2.北京邮电大学移动网络技术国家工程实验室，北京 100876）

1 引言

随着5G 的发展和移动终端设备的普及，日益涌现的移动应用及其产生的数据量将急剧增长[1]。其中，人脸识别、交互式在线游戏、虚拟/增强现实、4K/8K 超高清视频等时延敏感型、计算密集型的应用不仅需要消耗大量的计算资源，在用户服务质量方面也提出了超低时延、超高可靠性的要求。围绕6G 网络的总体愿景，未来移动通信网络将以智能简约作为设计内涵[2]，充分利用边缘泛在的计算能力，促使通信网络更加扁平化[3-4]。在云计算、移动边缘计算（MEC,mobile edge computing）的发展大趋势下，未来移动用户的周围将部署不同规模的边缘服务器以完成复杂任务处理，并利用通信资源完成计算任务数据的高效传输，逐步形成通信资源赋能“端−边−云”协同计算的新范式[5-8]。

为了满足人脸识别、虚拟/增强现实等计算密集型移动应用超低时延的服务需求，可以在靠近用户侧的边缘服务器上进行计算任务处理。由于单一边缘服务器能力有限，通常需要多个边缘服务器的协同处理，且涉及计算数据迁移、计算结果共享以及多维资源的使用。然而，泛在接入的边缘网络极易受到恶意节点的信息干扰或数据攻击，恶意节点可能篡改甚至伪造计算迁移请求、计算处理结果以及资源调度指令，破坏正常计算迁移、计算结果共享与资源调度进程。因此，在边缘侧环境异构开放、节点互不信任的情况下，如何保障计算卸载服务、计算结果共享和资源调度过程的安全可信与高效协同，是一个亟需解决的关键问题[9]。

目前，学术界和产业界普遍认为区块链技术是助力实现安全可信MEC 生态的关键技术[10-11]。区块链技术本质上是一种基于分布式对等网络的分布式账本技术，具有去中心化、不可篡改、可追溯、匿名性和透明性五大特征，这些特征为构建安全可信的分布式交易环境提供了良好的契机[12-15]。在区块链赋能的移动边缘计算（BMEC,blockchain-enabled mobile edge computing）系统中，在不需要第三方授权机构或平台背书的情况下，移动终端设备与边缘服务器之间可以自由发起计算卸载和资源调度请求，利用密码学原理，如非对称加密算法和哈希算法，可以对边缘资源调度指令、计算结果、交易记录等敏感信息进行保护与验证，同时利用共识机制，对服务与资源交易记录达成一致确认，进而保障资源与服务交易过程的安全、可信与透明[16-19]。然而，在区块链系统的共识过程中，需要利用计算及通信资源完成区块的生成、验证及传输等关键步骤，这对有限的计算资源和通信资源的高效调度提出了更高的要求。

在BMEC 系统中，不仅需要考虑移动用户的计算任务卸载请求，还需要考虑来自区块链系统的计算任务。值得注意的是，用户卸载计算任务和区块链系统的计算任务在并行处理方面存在较大差异。具体来说，用户卸载计算任务中的视频转码、人工智能推理、图像识别等高并行性计算任务可以被划分为大量相互独立的子任务进行并行计算，而其他复杂的计算任务如基于有向无环图（DAG,directed acyclic graph）的高斯消元和快速傅里叶变换，往往拥有不同程度的内部关联性，导致其在并行处理方面存在诸多限制。此外，BMEC 系统中的区块生成和验证也是一种高并行性计算任务。针对不同计算任务之间存在的并行性需求差异，众多学者和研究人员提出异构计算架构，联合优化中央处理单元（CPU,central processing unit）和图形处理单元（GPU,graphics processing unit）调度进行加速计算[20]。其中，CPU 一般只包含若干个单线程或多线程内核，仅可以实现粗粒度并行（CP,coarse-grained parallelism），对计算任务兼容性较好；GPU 通过装载数以千计的内核实现细粒度并行（FP,fine-grained parallelism），拥有强大的并行计算能力，但不适用于对复杂度较高的计算任务。针对BMEC 系统，异构计算架构可以满足不同计算任务的并行性需求，使计算任务的并行性类型与处理器类型相匹配，充分利用各种计算资源进行并行计算，达到降低计算任务执行时间的目的[20]。

在本文中，考虑到BMEC 系统中区块链计算任务和用户卸载计算任务的并行性需求存在差异，引入异构计算架构，优化CPU-GPU 异构处理器调度策略，联合分配通信和计算资源，实现系统性能的提升。考虑处理器调度约束、计算资源限制、通信资源限制，本文提出了联合优化处理器调度与资源分配（PSRA,processor scheduling and resource allocation）算法。本文的主要工作总结如下：1) 考虑不同计算任务的并行性需求，引入异构计算架构解决计算任务并行性类型与处理器类型之间的匹配问题；2) 考虑用户任务处理效率和系统区块生成效率占系统整体性能的权重，通过计算资源和带宽资源的合理分配，提升用户任务处理效率和系统区块生成效率。

2 相关工作

与本文相关的研究工作的介绍从以下三方面展开：区块链在MEC 系统中的应用、CPU-GPU 异构计算架构与应用、基于GPU 的区块链应用。

文献[16-19]主要针对BMEC 场景展开研究。文献[16]考虑了区块链系统区块最终生成时延与MEC 系统能耗之间的平衡问题，以两者加权和最小化为目标，将计算卸载决策、传输速率分配、区块生成调度、计算资源分配的联合优化问题建模为混合整数非线性规划（MINLP,mixed-integer nonlinear programming）问题，在解耦优化变量的基础上提出了迭代算法用于解决卸载决策和功率分配问题，并利用二分法解决了计算资源分配问题。针对传统卸载决策、资源分配、区块生成控制方法无法根据环境变化实时调整策略的缺陷，文献[17-19]将优化问题建模为马尔可夫决策过程（MDP,Markov decision process），并利用深度强化学习（DRL,deep reinforcement learning）算法进行求解。文献[17]采用联合基于股份授权证明（DPoS,delegated proof of stake）和实用拜占庭容错（PBFT,practical Byzantine fault tolerance）的共识机制，对BMEC 系统的计算卸载请求与处理结果进行记录并存储至区块链，提出了自适应的资源分配和区块生成方案，以提升由区块链系统吞吐量和边缘计算系统用户服务质量决定的系统长期奖励。为了实现长期计算卸载增益最大化并适应环境的高动态性，文献[18]研究了多跳网络中数据处理任务和区块挖掘任务的实时联合卸载控制问题，并提出DRL 算法对问题进行求解。以区块链系统交易吞吐量和MEC 系统计算速率最大化为目标，文献[19]对计算卸载决策、传输功率、块大小、块间隔进行联合优化，并针对决策空间同时存在离散决策和连续决策的特征，提出了基于异步优势行动者−评价家（A3C,asynchronous advantage actor-crigic）的DRL 算法。

考虑CPU-GPU 协同计算的模式，文献[21]设计了基于CPU-GPU 异构处理器的云计算架构，利用自适应分层、分层调度、性能估计等方法提升系统计算性能并降低计算和通信开销。文献[22]介绍了一种基于CPU 与GPU 的云计算平台Ankea，其是一个完整的平台即服务（PaaS,platform as a service）框架，包含用于应用程序快速开发的多种编程模型，支持基于分布式异构计算资源的编程模型部署。文献[23]针对视频编码过程中并行度较低的问题，提出了基于CPU-GPU 异构计算系统的多粒度并行计算方法，提升视频编码过程中并行执行的效率。文献[24]针对远程医疗数据加密时延较高的问题，提出了基于CPU-GPU 异构计算系统的加密函数调度优化算法。

GPU 加速计算在区块链系统中得到了广泛应用[25-28]。文献[25]基于不同规格的CPU、GPU 进行了包括比特币、以太坊在内的多类数字加密货币的挖掘测试，测试结果表明在数字货币挖掘的哈希速率方面，GPU 相较于CPU 有数十倍的速率提升。文献[26]同样利用基于统一计算设备架构（CUDA,compute unified device architecture）的GPU 提升了区块链挖掘效率，证明GPU 并行计算的优势只有当并行挖掘的任务数量大于800 时才得以体现。文献[27]针对区块链系统中大量用户搜索给全节点带来的计算瓶颈问题，利用区块链数据不能删除和更改的特征，引入适合GPU 并行计算的帕特里夏树（PT,Patricia tree）数组用于存储区块数据，实验结果表明基于PT 数组和GPU 的搜索吞吐量是基于CPU 的搜索吞吐量的14.1 倍。针对区块链系统中交易数据异常检测过程中的时延敏感、计算密集类任务，文献[28]将需要提取特征信息的交易数据缓存至GPU 存储单元中，并在GPU 中进行特征提取和异常检测，实验结果表明GPU 异常检测速率可以达到CPU 异常检测速率的37.1 倍。

与已有工作相比，本文考虑基于CPU-GPU 异构计算架构的BMEC 系统，以系统区块生成效率和用户任务处理效率共同决定的系统效用最大化为研究目标，建立异构处理器调度、计算资源分配、带宽资源分配的联合优化问题。本文将系统效用最大化问题建模为MINLP 问题。考虑到MINLP 问题的高复杂性，将原优化问题分解为处理器调度优化问题和资源联合分配优化问题，并对应提出了PSRA 算法。

3 BMEC 系统模型

本文考虑了基于异构计算的BMEC 系统，在边缘服务器上分别部署了CPU、GPU 两类处理器。本文将移动应用划分为低并行性普通应用和高并行性特殊应用（后文简称为普通应用和特殊应用），前者仅可以调用CPU 处理器，后者不仅可以调用CPU 处理器还可以调用GPU 处理器。异构计算实现过程如图1 所示，利用虚拟机（VM,virtual machine）技术，将边缘服务器中的CPU、GPU 计算资源虚拟化并分配给不同的虚拟机，以处理区块链计算任务和用户卸载计算任务。本文假设任意虚拟机仅可同时调用一类处理器处理计算任务，且两类计算资源可以按照任意比例分配给虚拟机。

3.1 网络模型

在本文中，利用区块链技术，BMEC 系统可以对多方共同参与计算卸载和任务执行信息进行记录，包括移动用户的计算卸载请求及任务处理结果等信息。值得注意的是，所有交易信息都先经过区块链共识节点的验证与确认，然后才会被存储至所有区块链节点备份中。BMEC 系统网络模型如图2所示。BMEC 系统主要由区块链用户、区块生成（BP,block producer）节点构成，BP 节点又分为主节点（PN,primary node）和备份节点（BN,backup node），具体介绍如下。

图1 异构计算实现过程

区块链用户。系统中的移动用户，可以提交计算卸载请求，边缘服务器完成计算任务并将处理结果反馈至移动用户。

区块生成节点。系统中的边缘服务器，不仅提供计算卸载服务，还负责区块的生成和验证。

主节点。在特定时间段从区块生成节点中选出的单个节点，被授权在该时间段生成新的区块。

备份节点。区块生成节点中除主节点以外的所有节点，负责新区块的验证工作。

交易信息。记录移动用户的计算卸载请求及任务处理结果，共享于整个区块链网络，由主节点收集并生成新的区块。

本文采用基于DPoS-PBFT 的共识机制[17]，假设M个边缘服务器（区块生成节点）以T为时延间隔轮流生成区块。服务器集合由∏={1,2,…,M}表示，m表示第m个服务器。假设恶意节点数量小于。简单来说，在指定时间内，PN 收集交易信息并将新生成的区块广播至所有BN 进行验证，即共识过程。当所有BP 节点达成共识后，新的区块才会被添加至区块链，然后被存储至所有区块链节点。

假设服务器m可用的CPU、GPU 计算资源分别为FC、FG（单位为cycle/s）。服务器中部署的应用集合表示为ψ={1,2,…,A}，A表示应用数量，a表示第a个应用。应用类型表示为ρa∈{0,1}，ρa=0表示a为普通应用，ρa=1表示a为特殊应用。假设任意服务器m服务于Nm个移动用户，用户集合表示为Γm={1m,2m,…,Nm}，nm表示由服务器m服务的第n个用户。此外，nm=0表示区块链计算任务。用户nm的计算任务可以表示为数组，其中am,n∈ψ表示任务所属的应用，αm,n表示任务数据量（单位为bit），βm,n表示利用CPU 完成计算任务所需要的计算量，γm,n表示利用GPU 完成计算任务所需要的计算量，ηm,n∈(0,1]表示计算任务对时延的敏感程度。由于不同种类应用对GPU 的利用效率不同，本文假设，其中Xm,n∈(0,1]表示计算任务nm对GPU 的利用效率，Xm,n由任务类型决定，Xm,n越大表明对GPU 的利用效率越高。本文考虑采用正交频分多址接入（OFDMA,orthogonal frequency division multiple access）方法，通信带宽资源被划分为数量为E的等带宽子信道，每个用户都可以被分配到若干个子信道用于无线传输。详细系统参数表示和相关含义如表1 所示。

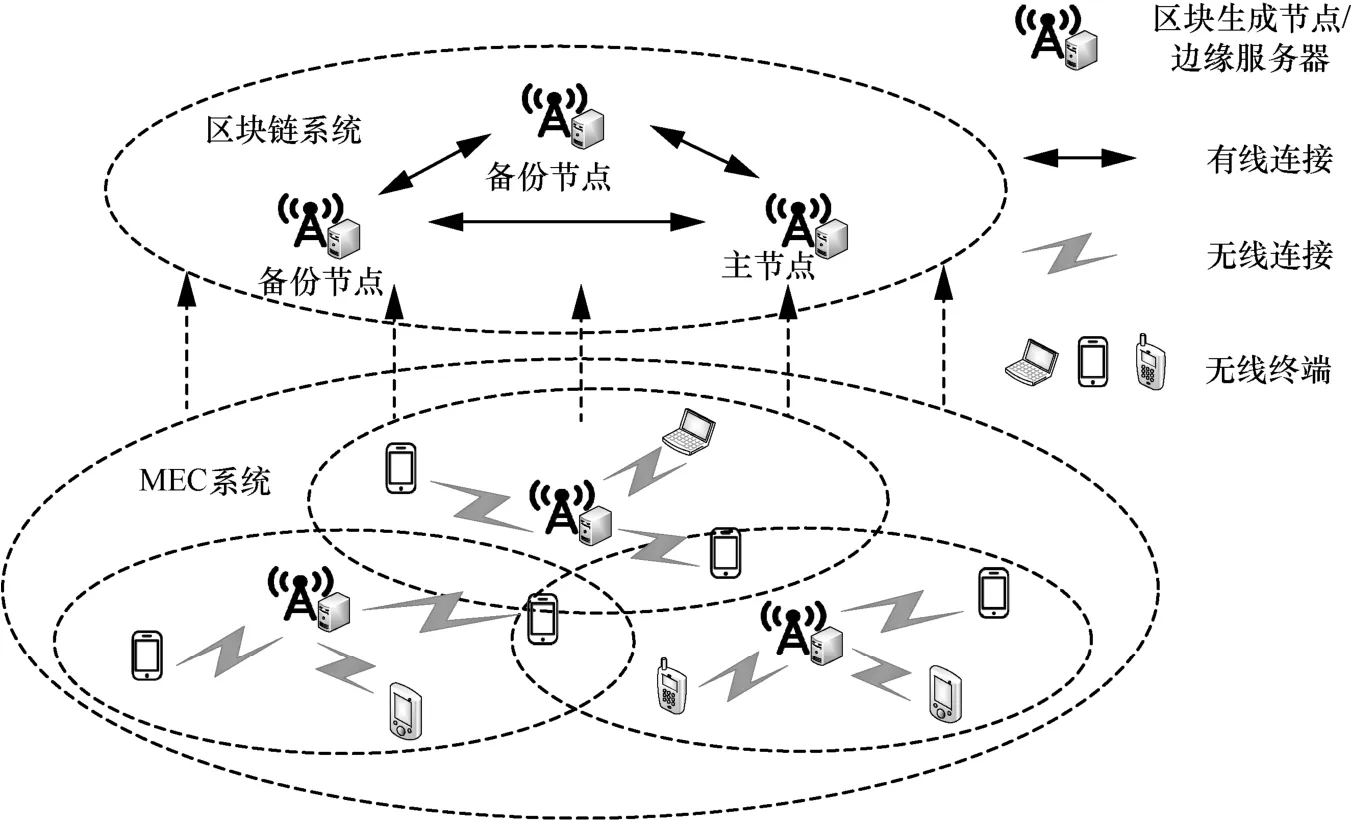
图2 BMEC 系统网络模型

表1 系统参数表示和相关含义

考虑到BMEC 系统中的计算负载分别来源于移动用户卸载的计算任务和区块链系统中区块生成、区块验证、达成共识所需要完成的计算任务，接下来将分别对区块链任务计算和用户卸载任务计算进行建模分析。

3.2 区块链任务计算模型

首先，移动用户向服务器发出卸载请求，服务器接受请求并处理任务；然后，将任务处理结果反馈至移动用户并将相关信息作为交易记录挂起等待PN 的进一步处理。PN 在收集交易信息并生成区块的时候，需要对交易记录中的用户签名（SIG,signature）和消息认证码（MAC,message authentication code）进行验证。PBFT 共识协议包含以下5 个阶段[17]：请求、序号分配、序号准备、序号确认、响应。

在请求阶段，PN 需要验证新区块中所有交易记录的SIG 和MAC 并生成新的区块，完成交易验证任务和区块生成任务所需要的CPU 计算量为，其中，SB、ϖ、φ、ϕ、g分别表示区块数据量、平均交易数据量、验证/生成SIG需要的CPU 计算量、验证/生成MAC 需要的CPU计算量、有效交易记录比例。

在序号分配阶段，PN 为新区块附上SIG 与MAC，并广播至所有BN。BN 收到新区块之后，需要验证新区块及其包含所有交易记录的SIG 与MAC。因此，此阶段在任意BN 处需要的CPU 计算量为。

在响应阶段，新区块经过BN 验证为有效区块后，所有BN 需要为新区块中的每条交易记录附加新的SIG 和MAC，然后将其传回PN。因此，此阶段在任意 BN 处需要的 CPU 计算量为。值得注意的是，序号准备与确认阶段，各BP 节点的计算需求量相对较小，本文忽略不计。

若服务器m为PN，则完成区块链计算任务的时延为

实时类应用往往需要其交易记录快速得到确认，因此，当服务器m为PN 时，系统区块生成效率为

当服务器m为BN 时，系统区块生成效率为

3.3 用户卸载任务计算模型

在用户卸载任务计算模型中，需要考虑移动用户卸载任务的时延和服务器处理计算任务的时延。用户nm的上行传输速率可以表示为，其中，Wm,n表示用户nm分配到的子信道数量，表示用户nm基于单个子信道的上行传输速率。因此，用户nm上传计算任务产生的时延为

在任务处理阶段，本文考虑每一个虚拟机都可以运行应用集合ψ中的任意应用，不同虚拟机可以同时运行相同的应用，但是一个虚拟机一次只能运行一个应用；服务器主机可以根据用户数量划分为数量相同的虚拟机，并将其与任务nm进行关联，然后根据任务需求给不同的虚拟机分配不同的计算资源。由于任意虚拟机只能同时调用一类处理器，且与用户nm关联的虚拟机的处理器调度决策可以表示为向量，λm,n=[0,1]表示调用 GPU，λm,n=[1,0]表示调用CPU。令向量表示计算资源分配策略，其中表示与用户nm关联的虚拟机所调用的CPU 资源数量，表示与用户nm关联的虚拟机所调用的GPU 资源数量。则计算任务nm的处理时延为

计算任务nm从上传至处理完成的总时延可以表示为。由于移动应用一般为时延敏感型，其任务完成时延直接决定了用户任务处理效率。因此，本文将用户任务处理效率定义为

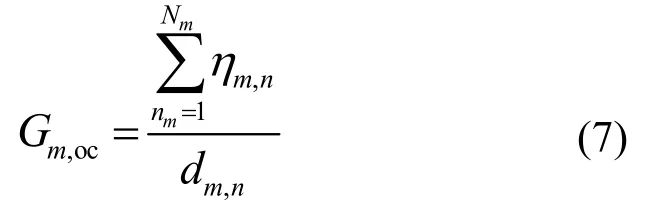
3.4 BMEC 系统计算模型

为了均衡系统区块生成效率和用户任务处理效率，本文将服务器效用函数表示为用户任务处理效率和系统区块生成效率的加权求和。当服务器m为PN 时，服务器效用函数为

C1 表示任意虚拟机仅可以同时调用一类处理器处理计算任务。C2 则给出了一般应用不能调用GPU 处理计算任务的限制，其中Γm,+={0∪Γm}，。C3、C4 分别给出了可分配CPU、GPU 计算资源的上限。C5 给出了带宽资源限制条件。C6～C8 则分别给出了不同变量的取值范围，分别表示维持虚拟机运行所需要的最低CPU 计算资源和GPU 计算资源，其中，有

C9 表示同时最多只能有一个服务器生成新的区块。由于所有服务器轮流生成新的区块，导致zm的取值是随机的，且当zm确定时，所有服务器的效用最大化问题是相互独立的。因此，C9 被松弛之后，原优化问题可以简化为面向任意服务器的系统效用最大化问题P2。

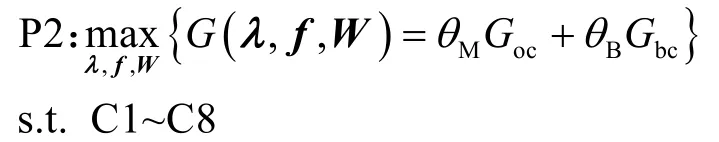
可以看出，P2 是一个典型的MINLP 问题，通常情况下此类问题没有有效的解决方法，需要根据具体模型设计解决方案。通过观察分析，原问题可以分解为2 个子问题，即资源分配优化问题和处理器调度优化问题。其中，在给定任意可行处理器调度策略λ的情况下，资源分配优化问题可以表示为P3。

令G(λ)=G(f*,W*)，其中f*和W*分别是调度策略为λ时的最优计算资源分配方案和最优带宽资源分配方案。优化问题P2 等价于处理器调度优化问题P4。

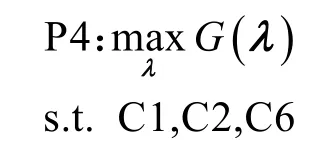
4 问题分析与算法设计

本节首先针对资源优化问题P3 提出基于拉格朗日对偶理论的资源分配算法，然后针对处理器调度优化问题P4 设计了基于任务处理时延的处理器调度与资源分配联合优化算法，最后对算法复杂度进行了分析。

4.1 资源分配优化问题

给定任意可行处理器调度方案λ，问题P3 的目标函数可以重新表示为

证毕。

因此，问题P5 可通过拉格朗日对偶法求解，且拉格朗日函数构造如下。

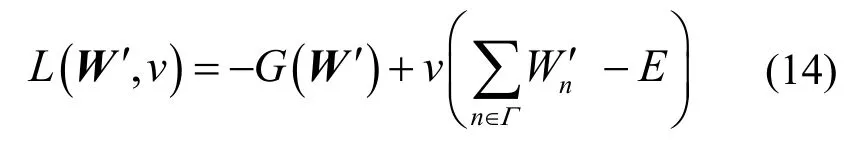
其中，v≥ 0为与C5'相关的拉格朗日乘子，限制条件C8'被暂时松弛。拉格朗日对偶函数可以表示为

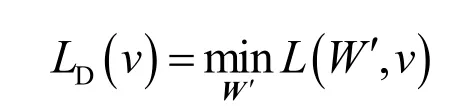
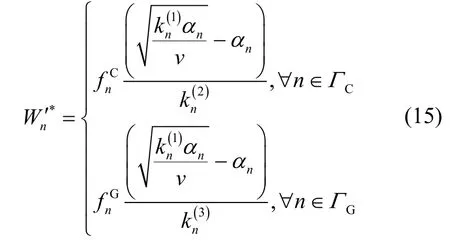
将W′*代入拉格朗日对偶函数可以获得关于v的对偶问题。由于对偶问题也是凸优化问题，可以得到，由此可以计算出

基于上述结论，本文设计了基于拉格朗日对偶的迭代算法对带宽资源分配方案进行优化，如算法1 所示。

算法1带宽资源分配算法

需要注意的是，带宽资源实际为离散变量，因此本文设计算法2，将W'*的连续变量转变为符合条件的离散变量。

算法2带宽资源分配方案转换算法

给定任意可行的带宽资源分配方案W，由于限制条件C3、C4 互相独立，优化问题P3 可以根据处理器调度决策解耦为2 个子问题P6、P7，分别对CPU 计算资源分配和GPU 计算资源分配进行优化。具体地，CPU 计算资源分配优化问题P6 可以表示为

GPU 计算资源分配优化问题P7 可以表示为

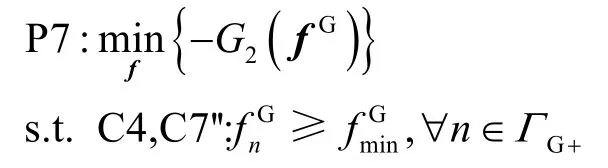
定理2问题P6、P7 是凸优化问题。

证明同定理1。

根据拉格朗日对偶理论，问题P6、P7 的拉格朗日函数分别构造为

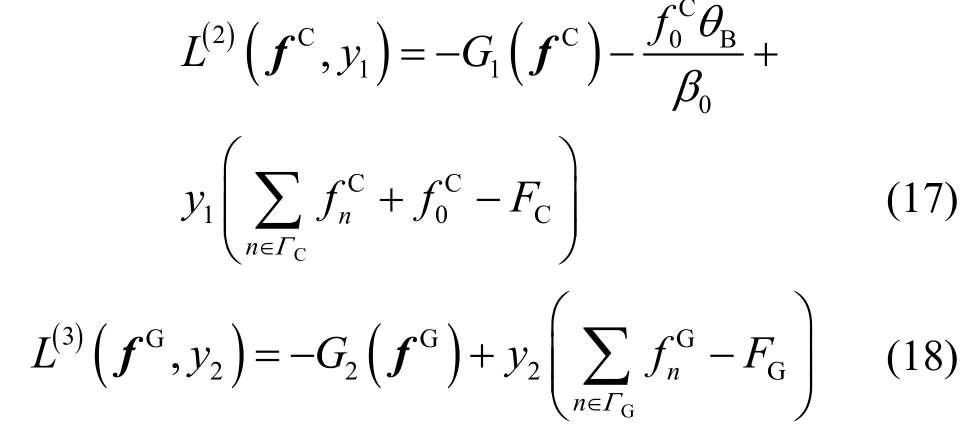
与之对应的拉格朗日对偶函数可以分别表示为

注意到上述获得的计算资源分配方案是基于假设λ0=[1,0]的。当λ0=[0,1]时，计算资源分配方案可以按照类似的方法进行优化，本文不再详细阐述。基于上述带宽资源分配优化方法与计算资源分配优化方法，本文设计了资源联合分配（JRA,joint resources allocation）算法，如算法4 所示。

算法4资源联合分配算法

初始化

4.2 处理器调度优化问题

根据限制条件C2 可知，与普通类型任务相关联的虚拟机只能调用CPU 处理器处理计算任务，由此可得。由于处理器调度策略可直接决定任务处理时延，从而影响系统效用，本文综合考虑任务处理时延和权重因子，设计了基于任务处理时延Tn的PSRA 算法对处理器调度问题（等价于问题P2）进行优化，如算法5 所示。具体地，加权任务处理时延定义为

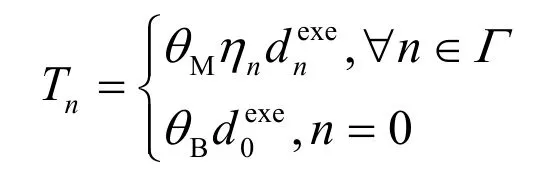
算法5处理器调度与资源分配联合优化算法

4.3 算法复杂度分析

PSRA 算法的计算复杂度主要来自处理器调度方案的迭代优化，假设迭代次数为I1。处理器调度方案每次迭代过程中的计算量主要来自JRA 算法对带宽资源及计算资源的迭代优化，假设迭代次数为I2。算法1 和算法3 的最大循环次数分别为N和N+1。因此，JRA 算法的计算复杂度可以表示为O(I2(2N+1))，处理器调度方案迭代优化的计算复杂度可以表示为O(I2(I1+1) (2N+1))，算法 PSRA 的总计算复杂度则可以表示为O(I2(I1+1) (2N+1)+N)。

5 仿真结果与分析

本节对基于异构计算的BMEC 系统性能进行了仿真测验和分析，并验证分析了所提算法相较于其他基准算法的优越性。首先描述了仿真参数设置，然后相继展示了所提算法的收敛性、优越性以及系统效用与用户数量之间的关系。

5.1 仿真参数设置

本文考虑的BMEC 系统中包含5 个MEC 服务器，每个服务器服务的用户数量为15，假设所有服务器均为区块生成节点，且每个节点轮流负责新区块的生成。本文考虑移动用户上行信道传输速率为随机变量[17]，假设每个用户在单位子信道上的上行传输速率均匀分布于[106,2 ×106]bit/s。本文假设每个服务器装配有6 个主频为2.4 GHz 的4 核8 线程CPU 处理器和一个主频为1 038 MHz 的768 核GPU 处理器[25,28]，即FC=57.6 Gcycle/s，FG=797 Gcycle/s。本文考虑每个服务器可处理五类应用，每类应用对应一种计算任务，每个用户随机产生其中一种任务，五类任务对应的应用信息如表2 所示。此外，区块链应用为特殊应用且GPU 利用效率为0.5，根据所有BP 节点轮流生成新区块的特征，本文假设区块链任务计算量满足概率，。其他仿真参数设置如表3所示。

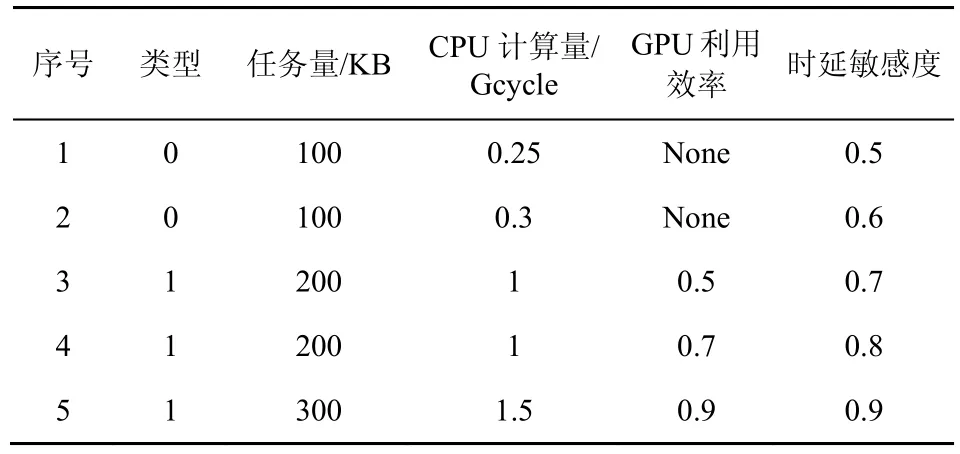
表2 应用信息

为了证实所提PSRA 算法的性能和异构计算架构引入的效果，本文将其与以下基准算法进行比较。

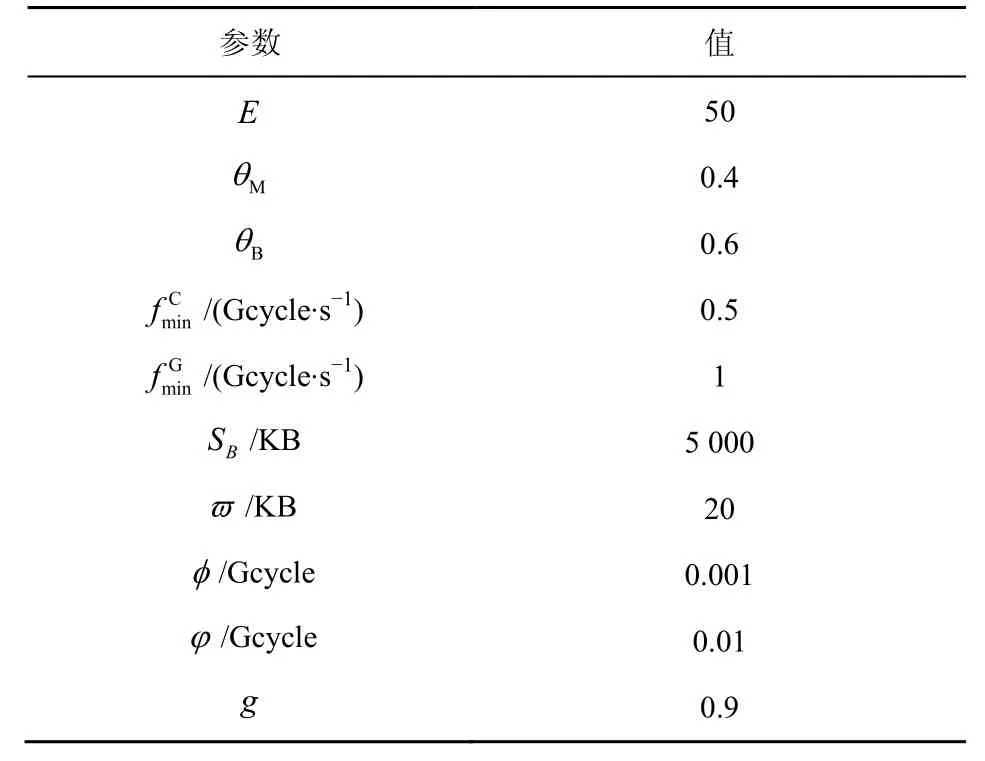
表3 仿真参数设置

1) 穷搜算法。列举所有处理器调度方案，找出使系统效用最高的处理器调度方案，资源分配采用JRA 算法。

2) 贪婪算法。凡属于特殊应用类型的任务，均调用GPU 处理器执行相关计算，资源分配采用JRA算法。

3) 资源平均算法。计算资源和带宽资源平均分配给每个用户，处理器调度策略基于PSRA 算法进行优化。

由于贪婪算法和资源平均算法未充分挖掘不同计算任务所存在的并行性，不能实现计算任务与处理器之间的匹配优化和异构计算资源分配优化，可视为未引入异构计算的基准算法。

5.2 算法收敛性

图3 和图4 分别表示用户数量为15 时，JRA算法关于计算资源分配方案和带宽资源分配方案的收敛性能。可以看出，2 种资源分配方案均在有限次迭代以后达到收敛状态。

图3 JRA 算法收敛性（计算资源分配方案）

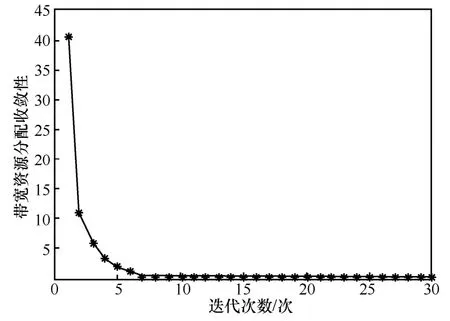
图4 JRA 算法收敛性（带宽资源分配方案）

图5 表示PSRA 算法在不同用户数量下的收敛性能。从图5 可以看出，随着迭代次数的增加，所提算法在不同用户数量的场景下均逐渐收敛。此外，当用户数量较少时，所提PSRA 算法的求解空间较小，可以更快收敛，而用户数量较大时，所提PSRA 算法的收敛速度降低。如图5 所示，当N=5时，所提PSRA 算法在平均迭代7 次后达到收敛状态。当N=15时，相比于N=5的场景，PSRA 算法需要更多迭代轮次达到收敛状态。因此，当平均迭代次数为7 次时，由于PSRA 算法在N=15的场景下尚未达到收敛，因此该轮次下的系统效用取值并不能反映系统效用随用户数量变化的相对趋势。当平均迭代次数为12 时，所提PSRA 算法在N=15的场景下达到收敛，此时该场景下的最终可达系统效用值高于N=5的场景。

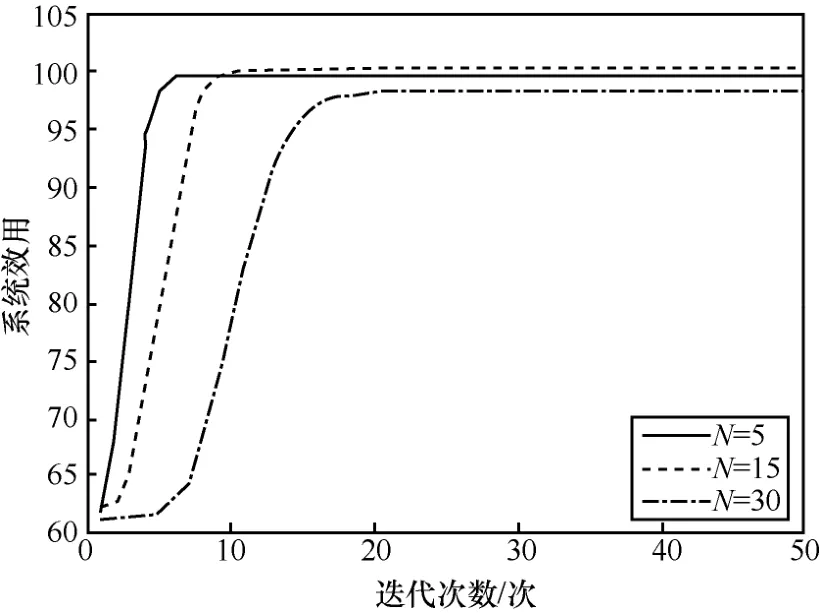
图5 PSRA 算法收敛性

本文定义的系统效用是由所有用户任务处理效率与系统区块生成效率的加权和决定的，系统效用函数不随用户数量增长呈现单调性。系统效用的取值受到带宽资源、计算资源、用户数量、用户任务处理效率与系统区块生成效率的权值等因素的综合影响。具体来说，随着用户数量的增加，系统效用函数中被累加的任务处理效率的数量随之增加；但是，由于随着用户数量的增加，每个用户可用的平均带宽资源、计算资源减少，区块生成任务可用计算资源也减少，导致单个用户任务处理效率及系统区块生成效率逐渐降低。

5.3 算法性能

图6 和图7 分别为N=5和N=15场景下PSRA 算法、贪婪算法、资源平均算法的性能曲线。由图6 和图7 可以看出，在不同的用户数下，PSRA 算法性能优于贪婪算法和资源平均算法。这主要是因为，针对不同种类计算任务的处理需求，PSRA 算法通过优化处理器调度和资源分配，可以有效提高用户任务处理效率和系统区块生成效率，进而提升系统效用。

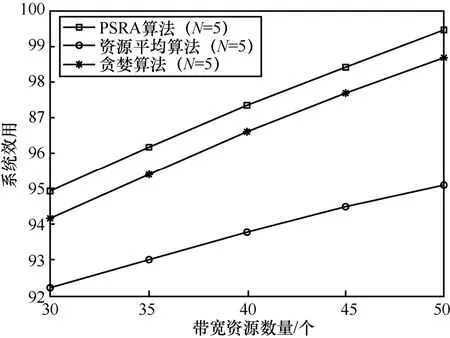
图6 PSRA 算法、贪婪算法、资源平均算法对比（N=5）

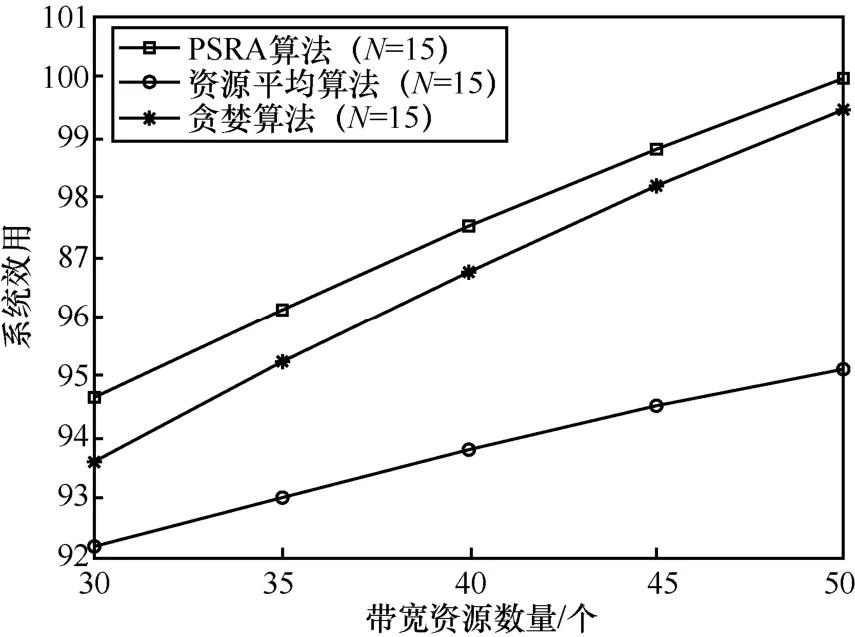
图7 PSRA 算法、贪婪算法、资源平均算法对比（N=15）

贪婪算法的优势在于可以根据任务需求优化带宽资源和计算资源分配方案，但是不能根据任务处理时延优化处理器调度方案；资源平均算法的优势在于可以根据任务处理时延优化处理器调度方案，但是不能根据任务需求优化带宽资源和计算资源分配方案。当带宽资源较少时，带宽资源平均分配方案与JRA 算法优化的带宽资源分配方案相对接近，此时带宽资源分配不均衡程度较低，优化资源分配方案所带来的系统效用增益较低。因此，当带宽资源较少时，资源平均算法的性能相对较好。但是随着带宽资源数量的增加，带宽资源平均分配方案导致的资源分配不均衡程度越来越高，通过优化资源分配可以获得较高的系统效用增益。因此，随着带宽资源的增加，资源平均算法与可以优化计算资源和带宽资源分配方案的PSRA 算法、贪婪算法相比，其算法性能会逐渐变差。

5.4 系统效用与用户数量的关系

图8 给出了PSRA 算法在带宽资源为50 时，系统效用与用户数量之间的变化趋势。由图8 可以看出，随着用户数量的增加，系统效用函数呈现先上升后下降的趋势。当带宽资源数量为50，用户任务处理效率和系统区块生成效率权重因子分别为0.4和0.6的情况下，N=15时的系统效用高于N=5和N=30的场景。然而，由于系统效用函数受到多重因素的影响，该相对趋势并不能体现系统的性能特征，系统效用不会随着用户数量的增长呈现出单调性特征。

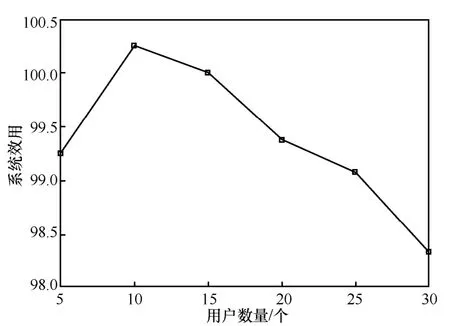
图8 系统效用与用户数量的关系

6 结束语

本文提出了一种基于异构计算的BMEC 系统模型，该模型通过联合优化异构处理器调度与资源分配，解决了联合处理移动应用计算任务和区块链计算任务时面临的高时延和资源利用率低下等问题。为了实现不同计算任务高效并行性处理，以系统效用最大化为目标，本文研究了异构处理器调度与资源分配的联合优化问题，并提出了基于拉格朗日对偶理论的处理器调度与资源分配联合优化算法进行求解。仿真结果表明，本文所提的PSRA 算法优于其他基准算法，可以有效提升基于异构计算的BMEC 系统效用。