适用于保密容量为负情形的基于混沌序列的polar 码加密方案

张小卉，张顺亮，李博文

（1.中国科学院信息工程研究所，北京 100093；2.中国科学院大学网络空间安全学院，北京 100049）

1 引言

为满足用户对移动通信业务低时延、超高传输速率等日趋增长的需求，5G 概念应运而生，其相关技术已成为学术界和产业界的重要研究热点[1]。5G 中的主要应用场景有如下3 种：增强型移动宽带（eMBB,enhanced mobile broadband）、海量机器类通信（mMTC,massive machine-type communication）和超可靠性低时延通信（URLLC,ultra reliable and low latency communication）[2]。其中，增强型移动宽带场景对于信道编码的主要要求为高吞吐量下具有较好的误码特性、较高的能量效率和较低的编译码时延。在众多信道编码中，polar 码是唯一被理论证明可达香农理论极限的信道编码[3]，具有较低的编译码复杂度，并且没有错误平层。polar 码凭借上述优越的性能被选为5G 通信标准中增强型移动宽带场景中的控制信息和广播信道编码方案。

然而，由于无线通信信道固有的开放传播性[4]，无线通信过程中的一些重要参数和数据容易被非法接收者窃听。窃听者可通过分析电磁信号以窃取有用信息，也可监听并分析通信过程中传输的信号，以上行为均会威胁到无线通信的安全性。在保障安全可靠通信的基础上，达到较高的安全传输速率一直是安全编码方案考虑的重要指标，polar 码是唯一被理论证明可达香农理论极限的信道编码，故研究polar 安全编码方案具有极其重要的意义。

随着计算机破译能力的增强，传统的加密机制难以保障通信系统的安全性，且实现复杂度较高，时延较长。数据链路层以上的加密方案并没有充分利用物理层信道的特征，当物理层数据传输不安全时，传统的加密方案难以保障通信的安全性。鉴于5G 中的eMBB 场景的需求以及物理层安全方案的优势，研究出安全可靠、高传输速率、低时延的polar码物理层加密方案尤其关键。现有的polar 码物理层加密方案大多基于Wyner[5]于1975 年提出的窃听信道模型，如图1 所示。

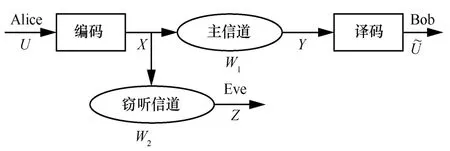
图1 窃听信道模型

在图1 所示的窃听信道模型中，Alice 和Bob是合法用户，Eve 是非法用户。Alice 试图与Bob通过主信道W1实现安全可靠的通信。与此同时，Eve试图通过窃听信道W2截获有用信息。U为二进制比特序列，表示Alice 试图与Bob 传输的信息，其长度为n；U被信道编码为X，X通过主信道W1和窃听信道W2发送出去。Bob通过主信道W1接收到信息Y并将其解码后得到，同时Eve通过窃听道W2获取信息Z。

在窃听信道模型中，信道编码通常由可靠性和安全性来衡量。Bob 获取到的信息可以用I(U;Y)来表示，泄露给Eve 的信息可以用I(U;Z)来表示。

信道编码的可靠性[6]条件为

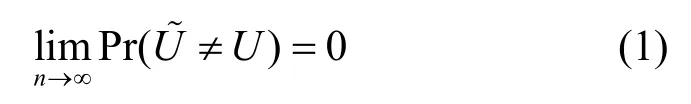
信道编码的强安全性[6]条件为

如果W1和W2为离散无记忆信道，则保密容量Cs[7]定义为

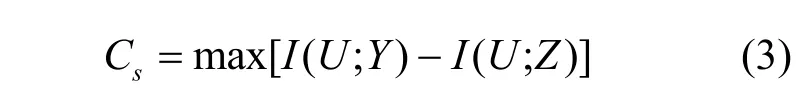
式(3)在U→X→(Y,Z)为马尔可夫链时可取到最大值。

如果W1和W2为对称离散无记忆信道，且W2为W1的物理降级信道，则保密容量可表示为[31]

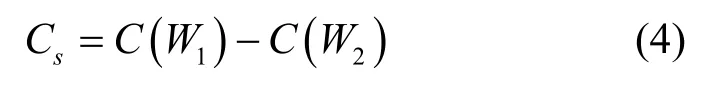
Wyner[5]指出保密容量为可达的安全传输速率的最大值，在保密容量为正数的前提下，采用安全编码方案传输速率可达到保密容量。

由式(4)可知，只有在满足主信道优于窃听信道的条件下，保密容量才为正数。然而，在实际应用中，往往存在保密容量较低或者为负的情形。较低的保密容量会限制安全传输速率，在实际应用中，常常以牺牲安全传输速率为代价保障安全性。此外，在实际情况中，难免存在窃听信道优于主信道的情形，即保密容量为负的情形，此时单靠安全编码方案已无法保证安全可靠的通信传输。因此，面向保密容量为负的场景，将加密技术和安全编码方案相结合可作为保证安全可靠传输的有效方案。

1.1 相关工作

基于以上窃听信道模型，很多学者提出了若干polar 码安全编码方案。其中，文献[8]基于对称窃听信道模型提出了一种多块polar 编码结构，该方案在确保可靠性和强安全性的前提下，安全传输速率可达到保密容量。基于文献[8]提出的多块polar编码结构，文献[9]将其扩展到非对称窃听信道和广播信道的应用中。相应的理论分析结果表明，文献[9]采用的polar 码编码方案可实现可靠性、强安全性，同时也达到保密容量。基于混沌理论，文献[10]将二进制混沌伪随机数发生器（BCPRNG,binary chaos pseudo-random number generator）与多块polar编码结构相结合，其主要用于产生二进制混沌序列对原始信息进行加密，且其密钥和密文一起进入polar 编码结构中。相关数学理论证明，该方案可实现密钥传输的强安全性，整个系统可实现可靠的传输。文献[11]在OFDM 传输模型中，引入混沌序列和polar 码，实验结果证明该方案不仅提升了误码性能，也在一定程度上降低了峰均功率比（PAPR,peak to average power ratio）。文献[12]在polar 码传输方案中设计了一种基于二进制混沌序列的加密方案，然而其所提出的加密方案具有较高的时延。文献[13]在可见光通信中对二进制混沌序列进行旋转变换以实现对polar 码的加密，可保证通信的可靠性、安全性。

文献[8-13]提出的polar 码安全编码方案均基于保密容量为正的前提。然而，在保密容量为负的情况下，以上文献中提出的polar 码编码方案不再适用。在实际应用中，窃听信道与主信道不存在必然联系，会存在保密容量为负的情形。为更好地应对一般性的通信场景，研究基于保密容量为负情形下的polar 码加密方案具有极其重要的意义。

文献[14]在保密容量为负的情形下，将BCPRNG 和polar 码结合，该方案在确保安全可靠传输的前提下，可实现正的安全传输速率。然而，该方案将密钥和密文置于polar 编码结构中传输，较长的密钥长度限制了安全传输速率。在该加密方案中，需要Alice 和Bob 提前获知第一块polar 码的密钥，且当前块的密钥需置于上一块编码结构中，由于BCPRNG 的引入，增大了系统的实现复杂度。本文提出了基于加密技术的polar 码安全传输方案，提升安全传输速率，并尽可能降低系统实现复杂度。

在众多加密技术中，RSA（Rivest-Shamir-Adleman）、DES（data encryption standard）等算法具有较高的实现复杂度，需消耗较高的计算资源，且对于被加密的比特长度有限制。基于混沌理论的加密技术具有随机性、初始值敏感性、遍历性、实现复杂度低的优点，本文将混沌加密技术和多块polar 码编码结构相结合，在保证通信的安全性和可靠性的基础上，实现较高的安全传输速率和较低的实现复杂度。

1.2 主要贡献

本文基于保密容量为负的情形，在对称窃听信道模型中，充分利用混沌序列的初值敏感性、遍历性、随机性，将混沌序列和多块polar 编码结构相结合，并充分利用冻结比特的设计，旨在设计可靠、安全、高传输速率、低复杂度的polar码加密方案。为降低系统实现复杂度，本文引入一维Logistic 混沌系统，相比BCPRNG，其实现复杂度较低，且其密钥为轻量级，可有效节约通信资源。

本文主要贡献如下。

1) 基于对称窃听信道模型，考虑保密容量为负的情形，提出一种可靠、安全、低复杂度、高安全传输速率的polar 码加密方案。

2) 基于数学推导，证明了方案的可靠性、安全性和高安全传输速率。

3) 基于不同的攻击场景，深度分析所提方案的安全性。

2 系统关键技术研究

2.1 polar 码

polar 码由Erikan 于2008 年提出，作为一种线性分组码，polar 码的实现主要基于信道极化原理。在二进制离散无记忆对称信道中，随着码长趋近于无穷大，polar 码可以达到对称信道容量[3]。相较于其他常用信道编码如LDPC（low density parity check）码、Turbo 码、RS 码等，polar 码具备较强的优势，主要体现为polar 码是被理论证明唯一可以达到香农极限的信道编码；polar 码不具备“误码平台”；polar 码编译码实现复杂度相对较低。下面，具体阐述信道极化原理和polar 码编译码过程。

对于一个二进制离散无记忆对称信道W：X→Y，其转移概率为，其中输入X取值为0 或者1，且0 和1 取值为等概率，码长为N。其信道容量[3]可表示为

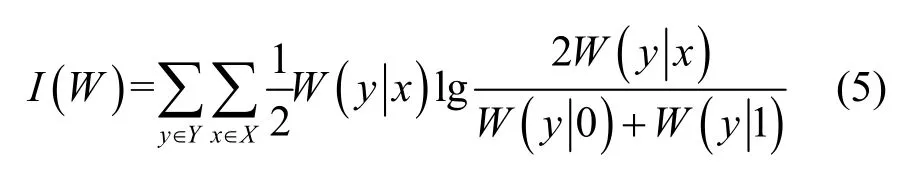
如果I(W)=1，则信道为无噪信道；如果I(W)=0，则信道为纯噪信道。

随着码长的增加，会出现信道极化现象，即信道会分裂出可靠信道和不可靠信道。其中常用的可靠性度量方法有巴氏参数法[3]、高斯近似法[15]和DE（density evolution）法[16]。其中巴氏参数法采用递归方法，且复杂度较低，故在polar 码传输方案中通常采用巴氏参数法。巴氏参数[3]相应的数学表达式为

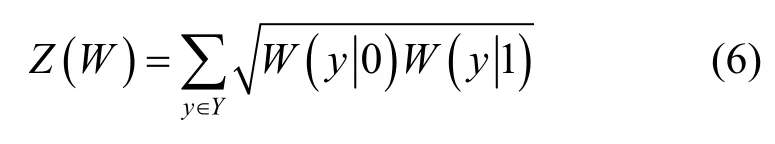
随着信息序列长度的增加，信道出现极化现象。其中信道容量趋于1，且巴氏参数趋于0 的信道称为可靠信道；信道容量趋于0，且巴氏参数趋于1 的信道称为不可靠信道。可靠信道用于传输信息比特，不可靠信道用于传输冻结比特，这样可保证信息传输的可靠性。

在图2 中，信息比特(μ0,μ1)被编码为(x0,x1)，其数学表达式为

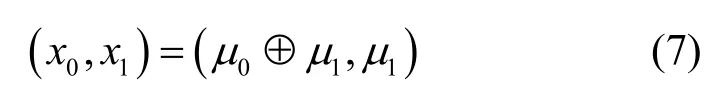
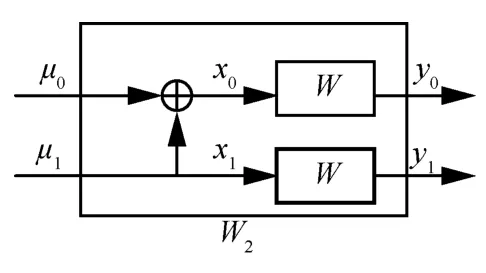
图2 一级信道极化

编码后的x0,x1分别经过信道W进行传输，合并后的信道表示为W2，其数学表达式为

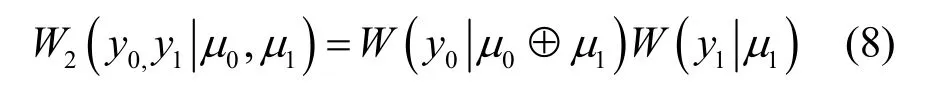
以上是一个一级信道极化过程，将此过程进行双重迭代，即可得到如图3 所示的二级信道极化过程，其数学表达式为

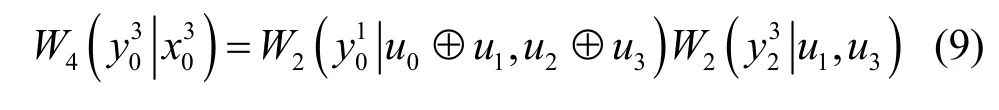
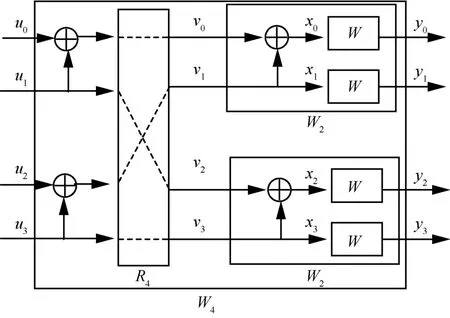
图3 二级信道极化

类似地，对上述操作进行多次迭代，可以实现多层级化，如图4 所示，其合并信道的转移概率[3]为

图4 N 级信道极化

polar 码的构造过程本质是一个信道选择的过程。如果polar 码长为N，信息位长度为K，对信道进行巴氏参数计算并按照巴氏参数对其排序，选择K个巴氏参数较小的信道索引构成信息位集合A，其余的N−K个信道索引构成冻结位集合Ac。集合A中的信道用于传输信息比特，集合Ac中的信道用于传输冻结比特。由此可见，通过比特索引即可判定信道是可靠信道还是不可靠信道。

在接收端，通常采用连续消除（SC,successive cancellation）[3]译码算法进行译码。第i位SC 译码的硬判决过程[3]可以表示为

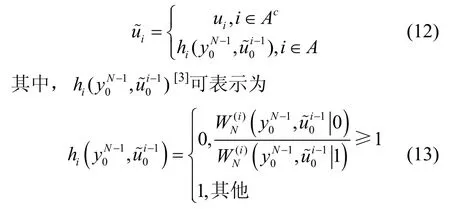
宏观而言，SC 译码是对信息比特按顺序进行逐比特译码，复杂度较低。SC 译码算法具备固有的误差传播现象，对于前序比特的译码错误会严重影响后续比特的译码[17]。

2.2 Logistic 混沌系统

混沌理论自提出以来引起了学者们深入的研究和关注。混沌序列已广泛应用于保密通信、语音加密、图像加密中[18-21]。作为非线性系统，混沌系统具有非周期性、初始值敏感性、随机性和遍历性的特征。此外，通过概率学理论很难预测和分析混沌系统的输出，具有不可预测性。

在众多混沌序列中，一维Logistic 混沌系统以其较低的实现复杂度获得了广泛的应用。为降低系统的实现复杂度，本文提出polar 码加密方案中采用Logistic 混沌系统。Logistic 混沌系统数学表达式[24]为

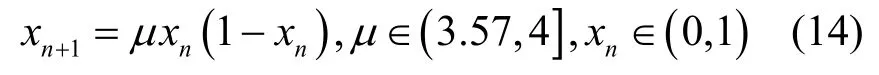
其中，μ为分岔参数。在μ∈(3.57,4]的条件下，系统处于混沌状态；在μ趋于4 时，系统表现出良好的混沌特性。

通常用Lyapunov 指数用来判别序列是否为混沌序列[22]，如果Lyapunov 指数大于0，则序列为混沌序列，其数学表示为

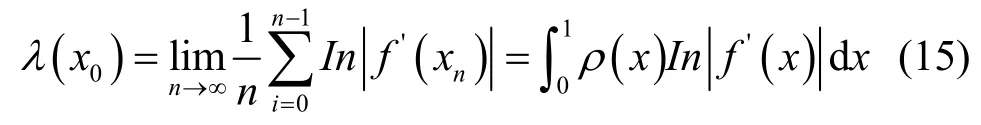
图5 为 Lyapunov 指数与μ的关系曲线，可以看出，在μ∈(3.57,4]条件下，系统处于混沌状态。

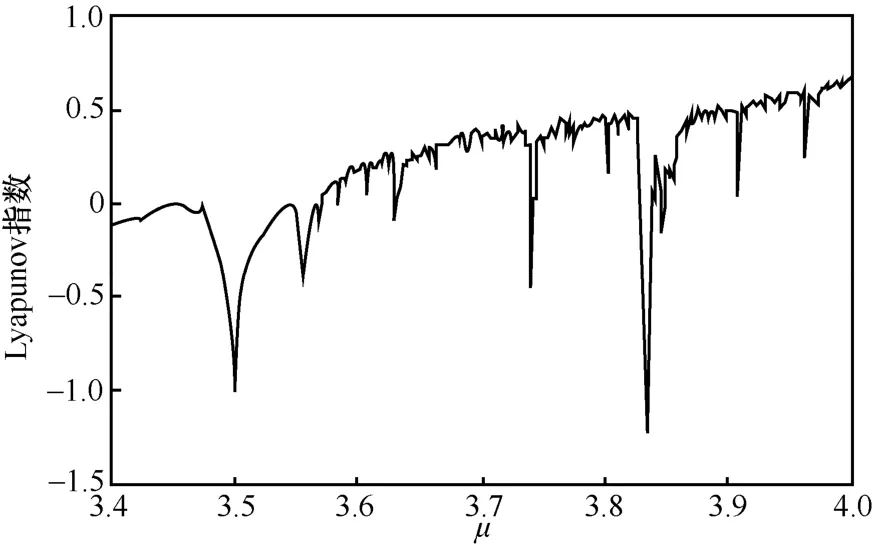
图5 Lyapunov 指数与μ 关系

图6 为Logistic 混沌系统的相空间结构，反映了x(n)和x(n+1)的关系。从图6 中可以看出，Logistic 混沌系统输出值在(0,1) 。在本文的加密方案中，将Logistic 混沌系统输出值离散化为0 和1，得到混沌二进制序列。

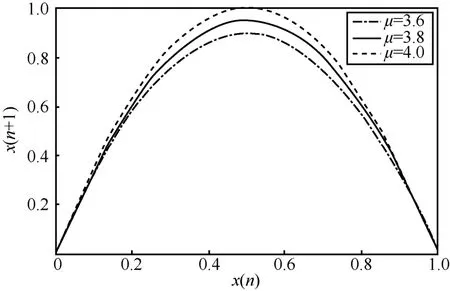
图6 Logistic 混沌系统的相空间结构

值得注意的是，Logistic 混沌系统具有初值敏感性。实验表明，在初值发生10−10数量级变化，进入Logistic 混沌系统经过大约30 次迭代时，其输出值会发生显著的改变[23]。

在本文提出的polar 码加密方案中，充分利用了Logistic 混沌系统的初值敏感性，合法通信双方基于物理层信道特征通过协商产生Logistic 混沌系统的初始密钥，由此产生的混沌序列经过离散化转换为二进制混沌序列，用于信息比特序列的加密和冻结比特的填充。

2.3 基于无线信道特征的密钥生成

无线信道特有的短时内互易性、时变性和空时唯一性，使其可以作为密钥生成的可靠来源[25]。由于无线信道的短时内互易性，无线信道在相干时间内会表现出相同的特性，这是通信双方获取共同密钥的基础。时变性保证了无线信道在不同的时间内具有不同的特征，进而可实现一次一密。由于空时唯一性，窃听者获取不到合法接收者所获取的信道特征，进而保障了安全性。

通信双方通过无线信道相关特征生成相同密钥，这样不需要额外传输密钥，也不需要中继节点进行密钥分发，有效地降低了复杂度，也增加了系统的安全性。基于无线信道特征的密钥生成主要由以下3 个步骤组成。

1) 生成原始密钥并量化

在相干时间内，合法的通信双方周期性地发送监测信号，以获得无线信道特征的相关数值。其中信道状态信息（CSI,channel state information）是无线信道提取密钥的重要参数，主要包含信道脉冲响应（相位和振幅）和信道频率响应，此外，也有一些密钥提取基于接收信号强度（RSS,received signal strength）和信道相位。

合法的通信双方使用相同的量化方法，获得共同的初始密钥。常用的量化方法主要包括多位量化方案[26]、双阈值量化方案[27]和基于交互量化误差的量化方案[28]。

2) 密钥协商

由于信道噪声干扰、检测错误等因素，合法的通信双方可能在初始密钥生成过程中产生不一致的信息位。因此，需要通过密钥协商过程获得初始密钥的高度一致性。

3) 安全增强

在信道检测和密钥协商过程中，非法接收者可能会窃听一些信息，威胁到密钥的安全性。因此，合法通信双方需采取安全增强方法防止非法接收者获取密钥的相关信息。当前，Hash 函数和提取器是常用的安全增强方法[29]。

本文在TDD 通信模式下，合法通信双方基于物理层信道特征在相干时间内提取的原始密钥，进行密钥协商、安全增强，最终将得到的比特序列进行一定的数学运算以生成Logistic 混沌系统的初始值和分岔参数。本文将混沌发生器用于基于物理层信道特征的密钥生成后的密钥扩展，并将生成的混沌序列离散化用于对于信息序列的加密和冻结比特位的填充，以确保密钥和传输信息的安全性。

3 基于混沌序列的polar 码加密方案

基于Logistic 混沌系统和多块polar 编码结构，本文考虑保密容量为负的情形，基于窃听信道模型提出了polar 码加密方案。如图7 所示，此编码方案主要由以下几个部分组成。

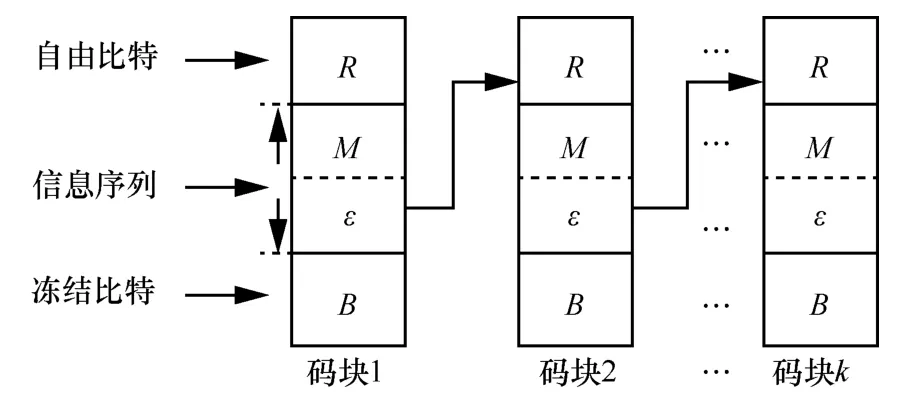
图7 polar 码多块编码结构

polar 编码。对主信道和窃听信道索引进行分集，在不同的信道集合放置不同类型的比特序列，进而保证系统的可靠性和安全性。

多块polar 编码结构。采用多块polar 编码结构将不同块连接起来。

混沌加密。基于无线信道特征产生Logistic 混沌系统的初始密钥，其中Logistic 混沌系统中的分岔参数和初始值作为密钥。生成的二进制混沌序列对原始信息比特进行加密，并对冻结比特进行填充。

定义 2 个信道，分别为W1：X→Y，W2：X→Z，其中W1和W2信道均为二进制输入对称无记忆离散信道，W1为Alice 和Bob 之间的合法信道，W2为Alice和Eve之间的窃听信道。本文假设W1是W2的物理降级信道。定义un为长度为n的待传输信息，经过polar 编码成为vn=unGn。根据信道极化理论，在信道W1中，随着n的增大，对于β<，信道索引集合为如下2 种分类。

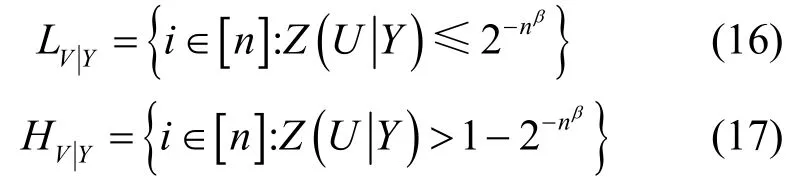
其中，属于LV|Y索引集合的信道，其对称容量随着n的增大趋近于1，巴氏参数趋近于0，称为可靠信道；属于HV|Y索引集合的信道，为不可靠信道。

类似地，在信道W2中，随着n的增大，对于，信道极化为如下2 种分类。

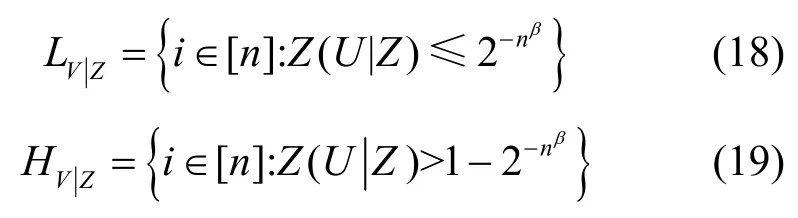
基于W1是W2的物理降级信道的假设，可以得到[9,30]。基于以上分类，本文将信道索引集合分为如下3 种：主信道和窃听信道均为可靠信道；主信道为不可靠信道，窃听信道为可靠信道；主信道和窃听信道均为不可靠信道。基于上述分类，定义如下集合

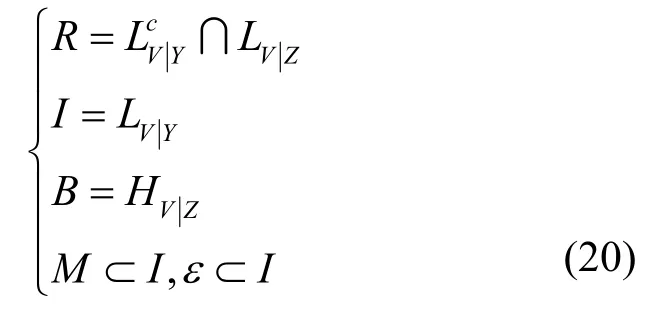
其中，集合为R的信道对于Bob 而言是不可靠信道，而对于Eve 而言是可靠信道，此类信道用于传输自由比特；集合为I的信道对于Bob 而言是可靠信道，用于传输信息序列；集合为B的信道对于Bob 和Eve 均是不可靠信道，此信道用于传输冻结比特；集合为M的信道用于传输加密信息。

在本文提出的polar 码加密方案中，采用了多块polar 编码结构和混沌加密相结合的方式。如图7所示，冻结比特放置于集合为B的信道中，自由比特放置于集合为R的信道中，信息序列放置于集合为M∪ε的信道中，其中上一个块的ε取值和当前块的R取值一致。

通过这样的多块编码结构，k个polar 码块连接在一起。通常情况下，冻结比特设置为全0，本文提出的polar 码加密方案中充分利用冻结比特的设计，将Logistic 混沌系统生成的二进制序列置于冻结比特中，其中Logistic 混沌系统的初始值和分岔参数为合法通信双方基于物理层信道特征生成，生成的Logistic 混沌序列经过离散化，一部分用于对信息序列的加密，另一部分置于冻结比特中。下面，介绍本文提出的加密polar 码方案加密编码和译码解密的具体过程。基于混沌理论的polar 加密编码结构如图8 所示。

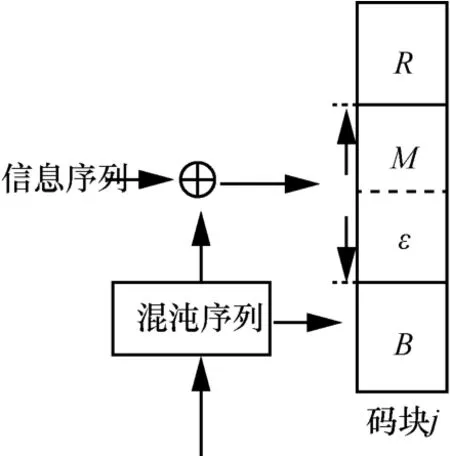
图8 基于混沌理论的polar 加密编码结构

如图8 所示，对于第j块polar 编码结构，合法通信双方基于无线物理信道特征获取生成的密钥(λ1,λ2)进入Logistic 混沌系统，生成值为(0,1) 的混沌序列，再经过判决产生二进制混沌序列。其中一部分二进制混沌序列用于加密原始信息，并将加密的信息序列存储至集合I=M∪ε中；另一部分二进制混沌序列存储至集合B中。

以上阐述了加密和编码的具体过程，下文详述Bob 接收到信息后的译码和解密过程。

通过以上步骤，Bob 即可完成译码和解密过程。

4 性能分析

4.1 可靠性

在本文提出的polar 码加密方案中，相应的误码率Pe可表示为

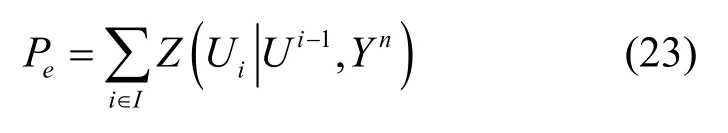
由于本文提出的polar 码加密方案采用SC 译码算法，由文献[3]可知

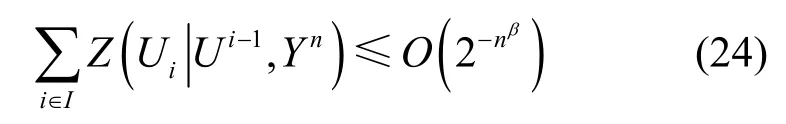
进而，可得

4.2 传输速率

本文提出的polar 码加密方案的安全传输速率Rs1可表示为

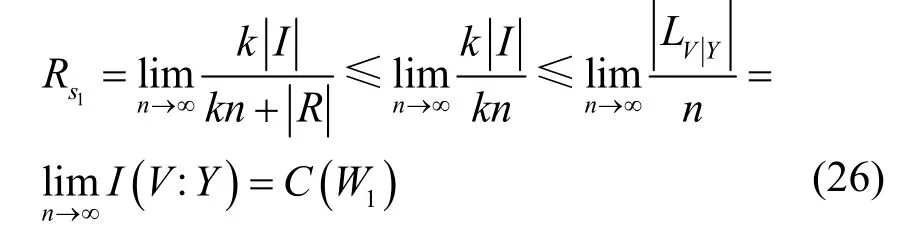
由式(26)可以看出，本文提出的基于混沌序列的polar 码加密方案的传输速率趋于主信道的信道容量。而文献[14]提出的polar 码加密方案中，其安全传输速率可表示为

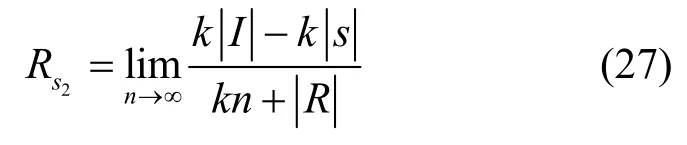
其中，s用于存储BCPRNG 的密钥，其传输密钥长度较长，对于安全传输速率的影响不容忽视。

在文献[8-9]中，polar 码加密方案的安全传输速率趋近于保密容量，具体可表示为

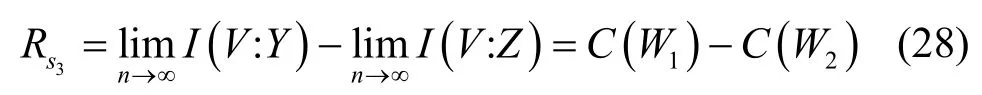
本文提出的基于混沌序列的polar 码加密方案有效地提升了安全传输速率，通过对混沌加密技术与安全polar 码编码方案的充分结合，确保了较高的安全传输速率，该方案不需要以降低安全性为代价，在负的保密容量条件下依然可达到较高的安全传输速率。

4.3 安全性

本文从窃听者Eve 的角度分析系统的安全性。在polar 码加密方案中，由于冻结比特由Logistic混沌序列产生，Eve 不能获取密钥 (λ1(j),λ2(j))，故只能采用SC 算法进行解密，具体表示为

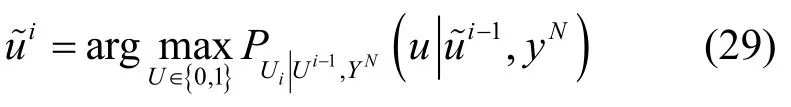
在SC 译码过程中，信息比特按顺序进行逐比特译码，对后面比特的译码会使用前面比特的译码信息比特估计值。SC 译码算法具有误差传播特性，因此如果前面比特译码错误，会增加后面译码的错误概率。

在本文提出的polar 码加密方案中，冻结比特和信息序列混合传输，由于Eve 无法获知密钥，故无法获知冻结比特。对于加密后的信息比特，Eve也无法解密，因而Eve 从接收到的信号中不能获取任何信息量，故，即Eve 截获到的信号Z和原始信息U互信息趋于0。

为进一步证实本文提出的polar 加密方案的安全性，从攻击场景角度展开分析。

在穷举攻击中，Eve 会采用数学统计的方法尝试破解Logistic 的密钥。然而，在本文提出的加密方案中，其密钥空间为(0.43 ×1010×1010)k，其中k为polar 码的块数，假设其为10，则密钥空间可达(0.43 ×1010×1010)10，约为0.2 ×10197。假设Eve 以每毫秒106次的计算速度破解密钥，则其需要的时间为0.6 ×10180年。显然，本文提出的polar 码加密方案具有足够大的密钥空间，足以抵抗穷举攻击。文献[32]指出密钥空间越大，安全水平越高，其对比了常用的通信物理层加密方法的密钥空间，并对比了RF（radio frequency） fingerprint、IS-95 CDMA（code division multiple access）、AES（advanced encryption standard）CDMA、Rand-MIMO（random multiple-input multiple-output）的密钥空间和破解所需要的时间。与常用密码方法相比，本文提出的polar 码加密方案具有较大的密码空间，所需要的破译时间较长，安全水平较高。

考虑一种极端情况，即Eve 正确猜测到了部分密钥，并且获知本文加密方案采用Logistic 混沌序列加密，但是Eve 无法获知具体的加密机制。该加密方案中采取了循环加密的方法，Eve 无从获知循环加密p的次数。即使Eve 获知了p的取值，由于对于信道分集规则不了解，故无法破解加密信息。然而，在文献[14]提出的polar 码加密方案中，会产生与信息序列相同长度的混沌序列，通过混沌序列与信息序列的异或运算进行加密。本文提出的polar 码加密方案充分利用物理层信道特征提取密钥，并且采用循环加密方法，相对于文献[14]提出的方案，本文提出的polar 码加密方案安全性更强。故本文提出的polar 码加密方案可最大程度地确保系统的安全性。

5 结束语

本文提出了一种可靠、安全、低复杂度、高安全传输速率的polar 码加密方案，适用于保密容量为负的情形。本文在TDD 通信模式下，合法通信双方在相干时间内生成基于信道特征的密钥，用于生成Logistic 混沌系统的初始密钥。由于Logistic 混沌序列的使用，系统实现增加的复杂度和开销较低，且其相应的密钥空间可达到(0.43 ×1010×1010)k，其中k为polar 码的块数，足以抵抗穷举攻击。由于信息传输中不包含密钥，因此polar 码加密方案可取得较高的安全传输速率。此外，通过充分利用冻结比特的设计以及利用混沌序列对信息序列进行加密，大大提升了窃听者的截获难度。通过相应的数学理论证明以及攻击场景分析可以得出，本文提出的polar 码加密方案具有可靠性、安全性，并且其安全传输速率高，能够很好地满足5G 通信中的高传输效率、低复杂度的要求，尤其适用于资源有限的通信场景。

本文未针对物理层信道特征提取密钥的具体算法展开深入研究，其中涉及具体的密钥提取和量化、密钥协商和安全增强的具体方法，有关密钥生成的具体算法会在后续工作中加强学习和研究。鉴于混沌序列的优良特性，在后续研究工作中，将对混沌序列在其他常用的新型通信技术中的应用展开深入学习和研究。