基于遗传和禁忌搜索混合算法的预制生产调度的研究

李 志，熊福力，汪琳婷，陈竑翰

(西安建筑科技大学 信息与控制工程学院，西安 710055)

0 引言

混凝土预制构件能流水生产能够发挥节能环保、缩短施工周期、减少劳动力等优势[1]。据调研，企业在流水生产混凝土预制构件时，大多依靠过往经验，导致库存紧张或者发生拖期，是构成装配式建筑成本居高不下的一重要因素[2]。所以，混凝土预制构件提前和拖期惩罚(ETP,earliness and tardiness penalty)问题是亟需解决的一类生产调度问题。

流水车间调度问题是一项非确定性多项式难(NP-hard,non-deterministic polynomial hard)问题，研究者通常采用人工智能算法求解相关问题[3]，尤其在预制生产方面，遗传算法使用居多。孟旭等[4]采用粒子群算法解决车间最大完工时间问题。谢思聪等[5]为解决预制构件流水生产调度问题，在GA的基础上融合了一种关于构件生产参数的定量方法。Leu 等[6]建立了预制构件混合生产的调度模型，并采用GA求解。Chan等[7-8]建立了预制构件流水生产的调度模型，并运用GA求解库存与拖期总加权惩罚最小化问题。Ko等[9]在解决预制构件流水生产相关问题时，考虑了相邻工作站间的缓冲区容量，并利用GA解决该问题。Yang等[10]建立了多条预制流水车间生产线的调度模型，最后通过GA解决提出的问题。Ma等[11]在多条流水线的基础上提出了重调度问题，并通过GA进行求解。Wang等[12]考虑了预制构件的整个供应链，并改进了传统的预制构件生产调度模型，最后通过GA解决提出的调度问题。

虽然GA已成功运用到预制构件流水生产调度问题中，但由于GA局部搜索能力较差，容易出现过早收敛的问题。考虑到TS算法的局部搜索能力较强，因此利用TS改进GA算法的局部搜索能力，提高解质量。

1 问题描述

预制构件流水生产的主要工序依次为：1)模具安装;2)钢筋放置;3)混凝土浇筑;4)蒸汽养护;5)模具拆除;6)瑕疵修整。预制构件根据生产工艺的特征，分为可中断和不可中断工序，其中不可中断工序为第三道和第四道工序，其余则为可中断工序。而且构件在养护阶段是并行处理过程，可同时养护多个构件。

预制构件企业在生产J个构件时，构件j发生拖期或提前完工分别会产生合同罚款和存储成本。每个构件都有与之对应的交货期(dj)、每单位时间的拖期惩罚成本(βj)、每单位时间的提前惩罚成本(ɑj)以及构件j在工序k的加工时间(pj,k)。

此外，在生产过程中满足以下条件：

1)构件都可以在零时刻进行加工，并在机器上以相同的顺序进行处理。

2)加工过程中禁止发生抢占活动。直到前一个构件完成为止，才可以处理下一个构件。

3)忽略机器故障等突发事件。

4)缓冲区大小和模具数量无限制。

2 调度模型

构件j的完工时间Cj小于交货期dj，则产生提前惩罚；如果Cj大于dj，则会产生拖期惩罚。预制构件流水车间ETP问题的目标函数为：

(1)

构件j的完工时间Cj可通过以下约束计算。

车间工作制度通常分为上班时间(HW)、非上班时间(HN)，其中非上班时间包含加班时间(HO)。

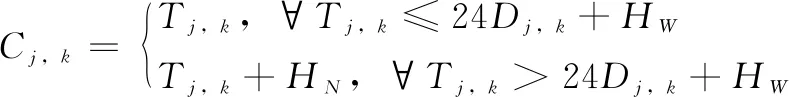
(2)

其中:公式(2)中k= {1, 2, 5, 6}；Tj,k是构件j在工序k的累加时间；Dj,k是构件j距工厂开机的工作日数。Dj,k是一个非负整数并且公式└·┘代表的是向下取整函数，Tj,k和Dj,k可分别由等式(3)和(4)计算得到：

Tj,k=max(Cj-1,k,Cj,k-1)+pj,k

(3)

Dj,k=|Tj,k/24|

(4)

混凝土浇筑工序的完工时间由下式表示：

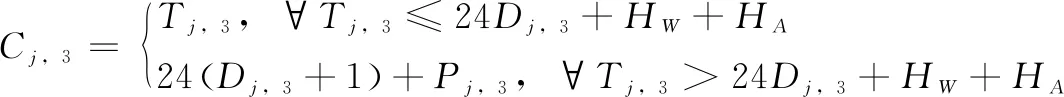
(5)

养护阶段对应的表达式为：

(6)

式中，Tj,4为构件的养护完工时间，Tj,4=Cj,3+pj,4

3 GA_TS算法

GA具有并行搜索能力，从解空间中多点出发搜索问题的最优或者近优解，适用于求解多种组合优化问题，但GA的局部搜索能力差，容易过早收敛。TS算法由于其灵活的记忆功能，以便跳出局部最优解，并转向解空间的其它区域，提高获得全局最优或近优解的概率。为了充分发挥两种算法的优势，提出了一种GA和TS的混合算法GA_TS，算法步骤如下：

1)设置GA_TS算法各参数，产生初始种群。

2)计算各染色体的适应度值。

3)通过选择、交叉、变异等算子更新种群。

4)将适应度值最优的染色体作为TS的初始解。

5)进行TS，得到局部最优解。

6)将TS得到的局部最优解替换种群中适应度值最差的染色体。

7)判断是否满足终止条件。若满足，停止迭代寻优；反之，转至步骤3)进行下次寻优。

3.1 编码方式

待加工构件的有J个，从区间[1,J]生成J个数字不重复的序列。染色体的编码示意图如图1所示，共有10个构件在流水线生产，构件编号按流水生产顺序依次为8，7，3，2，5，6，10，1，9，4。

87325610194

图1 染色体编码方案

一旦确定染色体内的基因内容，即构件排序，每道工序皆需按此顺序生产。

3.2 遗传算法

3.2.1 产生初始种群

种群由pop条染色体组成，每条染色均按小节3.1所述方式随机产生。

3.2.2 计算适应度值

在此步骤当中，通过目标函数公式(1)求得每条染色体i的目标函数值，再取其倒数作为该染色体的适应度值，即fit(i)=1 /f(i)。适应度值越大的染色体，被选择的概率越大。

3.2.3 选择

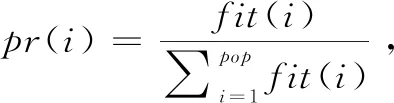
3.2.4 交叉

交叉在GA中起到关键作用，通常采用单点交叉和两点交叉。为了使种群能够多样性，采用两点交叉操作。两点交叉示意图如图2所示。

图2 两点交叉示意图

3.2.5 变异

变异操作是为了保证种群基因的多样性，避免陷入局部最优。变异操作的步骤为：在每条染色条内随机确定两个位置，交换这两个位置所对应的构建编号，如图3所示。

图3 变异示意图

最后由产生的子代更新种群。

3.3 禁忌搜索

3.3.1 产生邻域解

禁忌搜索的邻域解由Nsize条邻居解构成，每条邻居解根据当前解获得，主要需要两个步骤：首先随机选择当前解s中的两个索引位置，然后交换这两个位置的构件编号，即生成邻居解sN。交换操作如图4所示。

图4 两点交换示意图

3.3.2 禁忌表和禁忌长度

禁忌表主要作用是防止在搜索过程中避免陷入局部最优，从而可以搜索更多解空间。若禁忌表的长度太短，则搜索过程可能会进入死循环；相反，则导致计算时间太长。

禁忌表的长度代表每个禁忌对象的禁忌次数。

TS算法的伪代码如算法1所示。

算法1：

1):输入初始解s′，初始目标值f(s′)

2):设置禁忌长度tl，迭代次数TS_Iter，初始化禁忌表A

3):repeat

4):N(s′) ← 产生初始解s′的邻域解

5):f(s*) ←N(s′)中的最优目标值

6):iff(s*) >f(s′)，将解s*放入禁忌表A

7):更新禁忌表A，并令s′←s*,f(s′) ←f(s*)

8):记录目前最优解，S←s*

9): else

10):ifs*已被禁忌，选择邻居解中的次优解ssub放入禁忌表A

11):更新禁忌表A，并令s′ ←ssub

12):end if

13):end if

14):直至满足停止条件

15):return 目标解S，目标值f(S)

3.4 算法参数优化

算法通过Matlab 2018a编程实现，计算机配置为Microsoft Windows 10，处理器为Intel Core i5-7200U CPU @ 2.5 GHz，8 GB RAM。

为评估所提出的GA_TS算法的性能，GA和TS算法也将进行实验。GA有3个参数，分别是种群大小(pop)，交叉率(pc)和变异率(pm)。TS有两个参数，禁忌长度(tl)和邻域解数量(Nsize)。GA_TS有6个参数，分别为种群大小(pop)、交叉率(pc)、变异率(pm)、禁忌长度(tl)、邻域解数量(Nsize)和禁忌搜索迭代次数(TS_Iter)。

常用的算法调参的方法有田口方法和方差分析，其中田口方法主要适用于大于有两个参数的算法，方差分析适用于参数数量未超过两个的算法。所以GA和GA_TS采用田口方法调参，TS采用方差分析调参。调参结果如下：

1)GA：pop=80，pc= 0.9，pm= 0.1；

2)GA_TS：pop= 60，pc= 0.85，pm= 0.1，Nsize=J+10，TS_Iter= 55，tl=round((J×(J-1)/2))1/2)；

3)TS：tl=round((J×(J-1)/2))1/2)，Nsize=J+5。

4 实验结果及分析

为了评估各算法的性能，分别在20，30，50和70个构件数量进行实验，其中每种规模数量下各生成10个算例。工件的生产数据来源于[13]，列于表1，所有规模的构件数据皆是在此数据的基础上生成。构件j的交货期在区间[PT/J, 3*J]内随机产生，其中PT为所有工件的加工时间累加和。每个算例计算30次，记录30个值的最小值(Min)、平均值(Avg)、标准差(Std)。3种算法均在同一CPU计算时间内停止运行，其计算时间设置为800 ×Jms。

表2记录了3种算法的实验结果，其中3个算法在同一例子中的最小Min用粗斜体表示、最小Avg用粗体表示。表3统计了各算法在每种工厂规模下获得最好的Min、Avg、Std的算例数量，分别用符号No.Min、No.Avg、No.Std表示。

表1 预制生产数据

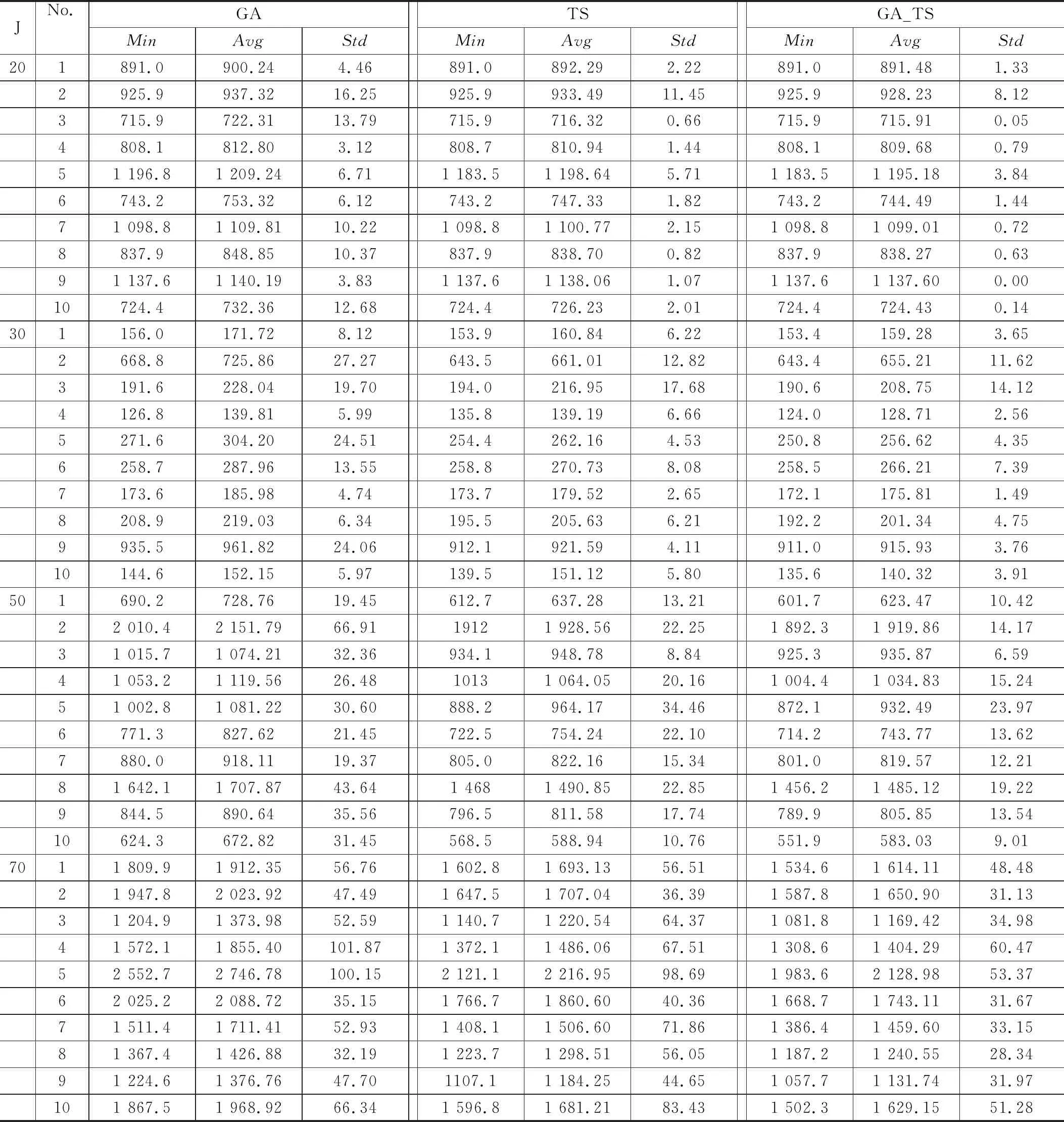
表2 两工厂规模实验结果

表3 结果统计

从表3的统计结果可看出，GA算法的最佳Min在40个例子中占10个，最佳Avg在40个实例中占0个；TS产生最好或相等的Min和Avg分别在40个实例中占到10个和0个；GA_TS算法的Min和Avg分别在40个实例中占到40个和40个。这表明在所测试的算例中，GA_TS的性能比TS和GA更为有效，求得的提前和拖期惩罚值更小。

从表3还可看出，在40个例子中，其中有GA_TS得到的Std值也小于TS和GA得到的Std值，这表明GA_TS比TS和GA具有更强的鲁棒性。为了更加清晰的表明提出的GA_TS算法的鲁棒性，作出了关于构件规模的平均标准差趋势图，如图5所示。

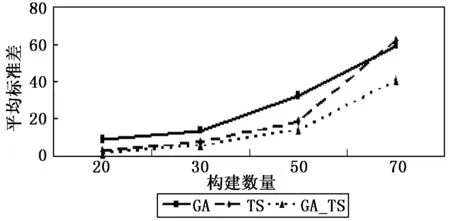
图5 关于构件数量的平均标准差趋势图

5 结束语

本文针对混凝土预制构件流水车间提前和拖期惩罚调度问题，建立了非线性整数规划模型。为了在合理时间内获得可行生产方案，提出了一种混合启发式算法—GA_TS算法，用其求解本研究所提出的调度问题。实验计算结果表明，提出的GA_TS算法在所测试的所有算例中计算得到的目标值、平均值以及标准差都要优于TS和GA算法，表现出了较强鲁棒性。继而可为实际生产提供理论性的指导以及技术性的服务。在未来的研究方向中，将机器故障、紧急插单等不确定情形集成到预制生产调度问题中，并开发出更有效的元启发式算法。