普通公路上占用外侧单车道的控制区长度研究
2020-11-02徐鹏徐珊珊
徐鹏 徐珊珊

摘 要:普通公路在发生交通事件后,由于事件占用部分车道,事发地易形成瓶颈,通行能力迅速下降。为了减少事件发生处的车辆排队现象,保证交通安全,避免二次事故。针对普通公路上交通事件占用外侧单车道的情况,探讨需要进行交通组织控制的区域大小。设计了Vissim实验,分析在不采取交通组织的情况下,影响车辆排队长度的因素;运用交通流理论,根据不同行车速度和大型车占比,计算控制区的长度;最后,使用Vissim微观仿真软件结合无锡市采集的交通数据进行实验。实验结果表明,使用车辆从进入控制区到完成一次换道行为所需要的总长度,作为控制区的长度能有效减少车辆排队长度。
关键词:交通组织;普通公路;控制区域;交通流理论;换道
中图分类号:U491.4
文献标识码: A
文章编号 1000-5269(2020)05-0114-06 DOI:10.15958/j.cnki.gdxbzrb.2020.05.18
目前,我国对公路的分类有多种方式。按使用功能和适应的交通量,可将公路分为高速公路、一级公路、二级公路、三级公路和四级公路5个等级[1]。普通公路则是指除高速公路外的一级至四级公路。
与高速公路和城市道路不同的是,普通公路的交通流构成包括机动车、非机动车、农用机械和行人等,且车辆行驶速度快,车辆超载现象严重,突发事件发生的可能性较高、事件的破坏性较大。普通公路一旦发生交通事件,将导致路段通行能力迅速下降。一般情况下,无法通过提高道路通行能力来解决事件带来的影响[2-3]。由于普通公路的周围环境复杂和半封闭特性,不管是可预期的还是不可预期的交通事件,都极易对该路段上的交通造成干扰,导致路网发生拥堵和排队现象。因此,采取及时的应急组织疏导交通、保护现场尤为重要。
对于交通应急组织的研究,当前学者主要侧重在城市路网和高速公路网的交通应急组织,国外主要集中在匝道控制[4-8]和主线可变限速控制[9-11]。国内在高速公路的应急组织方面:臧华等[12]利用车流波动理论推导出高速公路事件发生瓶颈处的排队长度,并进一步给出排队车辆数;张丰焰等[13]提出了在实施公路改扩建工程过程中,应对交通流进行路径引导和疏散,并提出了改扩建工程交通组织设计的原则和方法;在城市道路的应急组织方面,姚丽亚[14]等给出了事故条件下城市路网绕行路线选择方法,对于不同时段内的绕行交通量需求,确定不同的绕行路线,并分析了交通量重分配后的出行时间计算模型。
可见,目前对于交通事件应急组织的研究多针对高速公路和城市道路,对于普通公路的研究较少,因此研究普通公路上占用外侧单车道的控制区长度具有重要意义。针对普通公路突发交通事件占用外侧车道的情况,分析影响事件控制区的因素,利用交通流理论计算得到控制区长度,最后通过实验发现合理地设置控制区长度可以有效地降低车辆排队长度。
1 控制區影响因素分析
交通事件发生后,由于事件发生占用一定车道空间,使得事件发生路段通行能力下降,拥挤的交通波朝路段上游传播,影响上游的交通流状况。事件影响区划分为保护区、控制区和缓冲区。控制区指的是在事件保护区上游设置的用以减轻事发路段交通负荷、避免更严重的交通拥挤的区域[15]。
在该区域中,需要组织进入前方保护区的车辆,告知驾驶员具体的事件位置、交通堵塞信息、可能的延误时间,并强制车辆换道离开被占用车道,从而保证车辆在下游可以顺畅通过,提高道路通行效率,减少排队长度和行车延误。
1.1 仿真条件设置及参数选择
本文普通公路的设计速度为20~100 km/h,车道数为单向2车道至4车道。
按以下情况进行仿真:行车速度不变,调整大型车占比;大型车占比不变,调整行车速度。每车道交通量的变化范围为800~1 300 pcu/h,以100 pcu/h为仿真步长递增。
普通公路的车型组成复杂,且不同道路的大型车占比各异。因此,在Vissim中,设置交通组成为小客车和大货车,大型车占比变化范围为0.2~0.6,以0.1为仿真步长进行递增。
设计Vissim实验,利用在交通事件占用车道上设置信号灯的方式模拟事件的发生,并且在信号灯放置处设置局部路径。事件发生时,信号灯为红灯状态同时局部路径开放,信号灯放置的车道封闭,车辆沿局部路径从剩余未发生事件车道通行;事件结束时,绿灯开放,同时局部路径关闭,车辆恢复正常行驶状态。局部路径的长度即为道路封闭的长度,并设置检测器检测事件发生时的排队车辆数,得到排队车辆数与车速,大型车占比的变化关系。其他参数设置见表1。
1.2 仿真结果分析
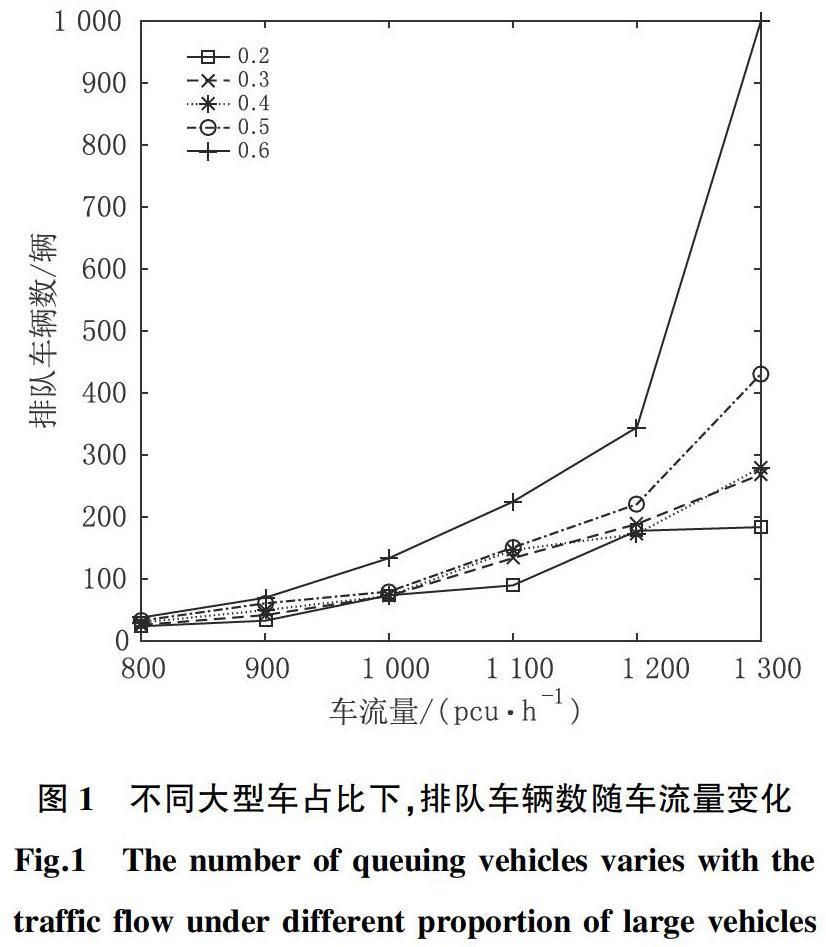
以单向3车道关闭1车道为例,在设计速度为80 km/h时,调整道路每车道车流量从800 pcu/h变化至1 300 pcu/h,大型车占比从0.2调整至0.6。对事件发生位置排队车辆数进行检测,得到结果如图1所示。
由图1可以发现:在道路条件和行车速度一样的情况下,当大型车占比一定时,排队车辆数随着车流量的增大而增大;当车流量一定时,排队车辆数随着大型车占比增大而增大,且大型车占比越大,排队车辆数增长的速度越快。
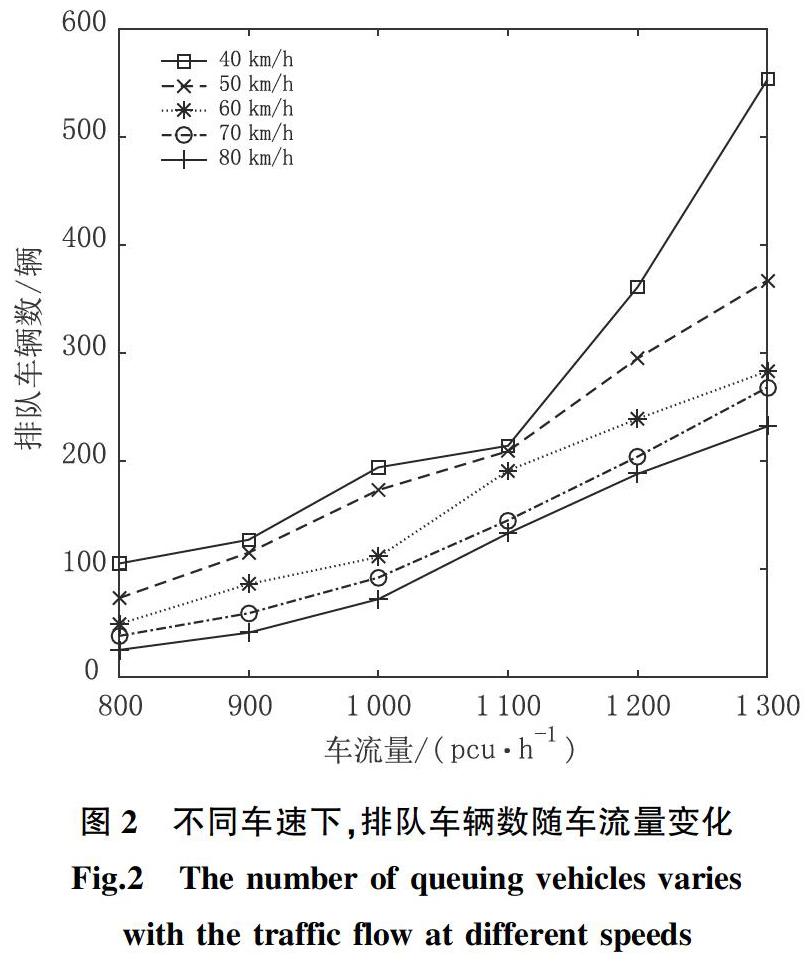
以单向3车道关闭1车道为例,在大型车占比为0.3时,调整车速从40 km/h变化至80 km/h,调整道路每车道车流量从800 pcu/h变化至1 300 pcu/h。对事件发生位置排队车辆数进行检测,得到结果如图2所示。
从图2可以发现:当道路条件相同,大型车占比不变时,排队车辆数随行车速度变慢而增大,随车流量的增大而增大;行车速度越慢,排队车辆数增大的速度越快。
由此可见,在不做任何交通组织措施的前提下,行车速度和大型车占比对事发路段排队长度有重要影响。根据不同的行车速度和大型车占比合理地设置控制区的长度,在控制区的起点处对即将进入控制区的车辆进行预警。驾驶员有充分的时间处理信息并进行减速操作,车辆可提前换道进入未受影响车道通行,大大减少排队长度和行车延误。
2 控制区长度确定
控制区长度组成如图3所示。由图3可见,驾驶员进入控制区时,部分车辆还位于被占用车道上。此时,驾驶员需寻找机会,在调整车速的同时找到临界接受间隙,向未受影响的车道换道。因此,控制区的长度对交通事件的疏导组织起关键作用。如果控制区的长度过短,车辆在控制区行驶结束时无法完成换道行为,则只能在保护区内排队等待换道,形成拥挤。同时,也会对其余车道内的车辆造成影响,导致其余车道内的车辆速度降低,甚至发生二次事故。
驾驶员进入控制区后,首先寻找换道机会,进行换道,换道完成后还必须与前车保持一定的安全距离。所以,该区域的长度与车流量、车速、司机反应时间相关。控制区长度计算公式如下:
式中:S为控制区总长度,m;S1为驾驶员从寻找换道机会到开始换道行为所行驶过的距离,m;S2为驾驶员从决定换道到完成换道行为所行驶过的距离,m;S3为驾驶员换道完成后与前车保持的安全距离,m。
2.1 寻找换道机会行驶过的距离
有换道意图的车辆必须要等待一个临界接受间隙,才能从被占用车道换道到目标车道。同时,驾驶员并不能立即做出换道反应,必须在判断并确认临界接受间隙后,才开始换道行为。所以,从寻找换道机会到开始换道行为所行驶过的距离可以表示为
式中:v1为当前车道的平均速度,km/h;tw为换道车辆等待一个临界接受间隙的平均时间,s,计算如式(3)所示;tr为驾驶员判断临界接受间隙并确认开始换道行为的反应时间,据文献[16]取1.5 s。
车辆等待目标车道出现临界接受间隙的平均时间为
式中:λ为车辆平均到达率,辆/s;Q为交通流的流量,辆/h; P(h≥t)为车头时距h≥t 时的概率; t为车辆临界接受间隙,s;τ为最小车头时距,一般取值 1.5 s。根据文献[17]可知小型车、大型车的临界汇入间隙均值分别为3.96 s和5.04 s。
2.2 换道过程行驶过的距离
计算换道过程行驶过的距离要考虑车流间的相对运动,一般认为车速要降低到以相对目标车道20 km/h的速度运动,则驾驶员换道过程中行驶过的距离按下式计算:
2.3 与前车保持的安全距离
完成换道之后,车辆和前车应当保持一定的安全距离,避免前车突然刹车,后车来不及避让而发生二次事故。安全距离计算如下:
式中:v3为控制区限制车速;i为坡度,上坡为“+”,下坡为“-”;φ为车道纵向摩阻系数,与路面种类和状况有关。
3 算例
以江苏省无锡市G312天一高架至洛新高架路段施工事件为例,计算交通事件控制区的长度。设计Vissim实验验证以驾驶员在控制区内完成一次换道所需要的长度作为控制区的总长度,可有效降低由事件造成的行车延误,降低排队长度。
3.1 计算控制区长度
如图4所示,江苏省无锡市G312天一高架至洛新高架路段进行养护应急大中修施工。施工时间为2018年5月7日晚上20点至2018年5月15日凌晨6点,施工期间封闭1股车道,早上6点结束施工,恢复交通。
经过现场调查发现:该施工路段为双向6车道一级道路,路面宽度40 m,车道宽度4 m,设计速度为80 km/h,保护区内限制速度为40 km/h,控制区内限制速度为60 km/h,车道纵向摩阻系数为0.4。分析2018年5月1日至2018年5月6日,由G312胜丰(观测站编号G312L121320206)获取的数据,晚上8时至早上6时,平均小时车流量为965 pcu/h,高峰小时平均车流量可达到2 310 pcu/h。其中,小型车占比为68.47%,大型车占比为31.53%。为了达到疏散交通减少排队的目的,取高峰小时平均车流量2 310 pcu/h计算车辆到达率。
首先计算S1長度,根据式(2)—式(5),分别计算得到小型车所需S1长度为84 m,大型车所需S1长度为192 m,根据小型车与大型车的占比,取加权平均数118 m作为S1长度。
根据式(6)计算得到S2长度为329 m。
根据式(7)计算得到S3长度为35 m。
根据式(1),控制区长度为482 m。
3.2 模型验证
参考江苏省无锡市G312胜丰(观测站编号G312L121320206)获取的数据,每车道车流量输入范围为300~900 pcu/h,以100 pcu/h为仿真步长,设置小型车占比为68.5%,大型车占比为31.5%。结合无锡路网的实测数据,使用Vissim微观仿真软件进行仿真。检测事件影响区排队车辆数,如图5所示。
从图5可以看出:随着车流量的变大,排队车辆数也越多,在900 pcu/h时达到最大值;而随着车流量的增长,未设置控制区时的排队车辆数增长速度与设置控制区后相比更快。因此,在控制区的起点处对驾驶员进行预警并让驾驶员离开事发车道,可有效降低排队长度,提高行车效率。
4 结语
本文研究发生交通事件后采取交通组织控制的区域长度,利用Vissim仿真实验分析影响控制区长度的因素并使用交通流理论计算控制区的长度,得出以下结论:
(1)不同的行车速度和大型车占比对控制区长度的影响不同,越高的大型车占比和行车速度,需要的控制区长度应越长。
(2)控制区的长度必须满足上游车辆进入控制区后完成寻找可汇入间隙、进行换道和换道后与前车保持一定安全距离这3个过程的长度要求。
(3)将车辆完成一次换道并与前车保持一定的安全距离所需的长度作为控制区长度可以有效降低事件发生后的排队长度。
虽然对普通公路交通事件占用外侧车道的控制区长度进行了研究,但是仍有一定的不足之处,长度影响交通控制区域长度的因素复杂,本文只选取了行车速度和大型车占比,且没有对控制区内的车速限制进行进一步的研究,在今后的研究中应进行完善。
参考文献:
[1]交通运输部公路局. 公路工程技术标准:JTG B0l-2014[S]. 北京: 人民交通出版社, 2014.
[2]陈茜, 王炜. 大型活动中突发事件对交通流的时空影响[J]. 交通运输工程学报, 2009, 9(3): 81-85.
[3]翟忠民. 道路交通组织优化[M]. 北京: 人民交通出版社, 2004: 352.
[4]PAPAGEORGIOU M, BLOSSEVILLE J M, HAJ-SALEM H. Modelling and real-time control of traffic flow on the southern part of Boulevard Peripherique in Paris: part II: coordinated on-ramp metering[J]. Transportation Research Part A General, 1990, 24(5): 361-370.
[5]HADJ-SALEM H, BLOSSEVILLE J M, PAPAGEORGIOU M. ALINEA: a local feedback control law for on-ramp metering; a real-life study[C]//International Conference on Road Traffic Control, USA: IEEE Xplore, 1991: 194-198.
[6]DIAKAKI C, PAPAGEORGIOU M, MCLEAN T. Simulation studies of integrated corridor control in Glasgow[J]. Transportation Research Part C Emerging Technologies, 1997, 5(3/4): 211-224.
[7]CHI R, HOU Z, JIN S, et al. A data-driven iterative feedback tuning approach of ALINEA for freeway traffic ramp metering with paramics simulations[J]. IEEE Transactions on Industrial Informatics, 2013, 9(4): 2310-2317.
[8]KACHROO P, RATLIFF L, SASTRY S. Analysis of the godunov-based hybrid model for ramp metering and robust feedback control design[J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(5): 2132-2142.
[9]HADIUZZAMAN M, QIUTONY Z. Cell transmission model based variable speed limit control for freeways[J]. Canadian Journal of Civil Engineering, 2013, 40(1): 46-56.
[10]YU R, ABDEL-ATY M. An optimal variable speed limits system to ameliorate traffic safety risk[J]. Transportation Research Part C, 2014, 46: 235-246.
[11]MLLER E R, CARLSON R C, KRAUS W, et al. Microsim-ulation analysis of practical aspects of traffic control with variable speed limits[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(1): 512-523.
[12]臧華, 彭国雄. 城市快速道路异常事件下路段行程时间的研究[J]. 交通运输系统工程与信息, 2003, 3(2): 57-59.
[13]张丰焰, 周伟, 王元庆, 等. 高速公路改扩建工程交通组织设计探讨[J]. 公路, 2006 (1): 109-113.
[14]姚丽亚, 魏连雨, 李春宝. 区域路网中交通事件影响范围及诱导分析[J]. 河北工业大学学报, 2005, 34(2): 24-27.
[15]许秀. 事故条件下高速公路网应急交通组织方法研究[D]. 南京: 东南大学, 2016.
[16]杨林, 邢翠芳, 赵海冰. 汽车跟驰状态下驾驶员反应时间研究[J]. 计算技术与自动化, 2015, 34(3): 33-37.
[17]关羽, 张宁. 可变临界间隙条件下的加速车道车辆汇入模型[J]. 公路交通科技, 2010, 27(6): 117-120, 126.
[18]吴江玲, 张生瑞, 秦思, 等. 高速公路施工区车辆强制换道耗时生存模型[J]. 哈尔滨工业大学学报, 2017, 49(9): 47-50.
(责任编辑:周晓南)
