基于卡尔曼滤波的GM(1,1)在变形监测中的应用研究

王 强 ，吴 盛 ，杨 静 ，任 军

(1.湖州吴兴东成测绘有限公司，浙江 湖州 313000 ； 2.中国水利水电第八工程局有限公司科研设计院，湖南 长沙 410000)

随着社会经济的发展，建设水平的提高，随之各种高层建筑、大型工业建筑、大坝等也不断涌现，对这些建筑物进行施工或者是建筑物在运营期间，一些外在影响因素会导致建筑物产生变形，当变形量超过相关规范规定的范围，就会对工程进度产生一定的影响，如果没能及时采取相关措施，甚至会产生安全事故[1]。显然，对这些建(构)筑监测就显得更加有必要。为了掌握建筑物变形的规律和趋势，可以通过对变形物体进行合理的监测，数据分析的结果也会给施工决策者提供指导意义[2]。在对监测数据处理和分析建模中，国内外学者已提出多种变形预测模型。主要有：灰色系统分析、回归分析、时间序列分析、卡尔曼滤波模型和工神经网络模型等[3]。刘江等[4]将小波和时间序列模型结合在一起，应用于郑州地铁2号线变形监测。朱军桃等[5]将马尔科夫与灰色模型组合对基坑进行变形监测，精度相对单一模型有所提高。

在实际监测数据采集过程中，外界环境复杂多变，在采集数据过程中也会带来其他扰动误差，这使得监测数据跳动很大，且数据信息量也很少。对此，在实际工程应用中，很难对变形物体有一个准确的预测。在数据建模过程中，随机扰动误差较大的数据用卡尔曼滤波剔除，可以使原始监测数据曲线变得平滑，拟合效果增强；在针对信息量少、样本小等问题，灰色模型可以很好解决此弊端。本文提出将卡尔曼滤波与灰色模型结合起来，建立组合模型，对大坝沉降进行变形预测，分析并检验预测数据的准确性和精度。

1 卡尔曼滤波的GM(1,1)模型

1.1 卡尔曼滤波

现代控制理论中用来剔除随机干扰误差的重要方法之一是卡尔曼滤波法，其原理是通过输入观测数据，建立线性系统状态方程，输出结果数据[6]。状态系统可以表示为连续性和离散型，变形监测采集的数据都是程离散状态，因此，本文在对卡尔曼滤波线性系统研究中，仅对离散系统进行介绍。

通过相关研究结论中得出，在离散系统的卡尔曼滤波建模中，主要通过观测方程数学模型和状态方程数学模型来实现，其离散化形式表示为：

Xk=Fk/k-1Xk-1+Gk-1Wk-1

(1)

Lk=HkXk+Vk

(2)

式中，Xk、Lk、Vk分别为系统k时刻n×1阶状态向量、观测向量和噪声矩阵；Fk/k-1、Gk-1、Wk-1分别为k-1时刻状态转移矩阵向量、动态噪声矩阵向量(n×r阶)和动态噪声矩阵向量(r×1阶)；Qk(非负定方差矩阵)为Wk-1的协方差矩阵；Rk(正定方差矩阵)为Vk的方差矩阵。

随机离散线性系统的Kalman滤波递推公式可以根据最小二乘原理推理得到。具体步骤如下：

状态向量一步预测值为：

(3)

一步预测方差矩阵为：

(4)

状态向量估计值为：

(5)

状态向量估值的方差阵为：

Pk(I-JkKk)Pk/k-1

(6)

式中，J为滤波增益矩阵，其具体形式为

(7)

通过以上步骤实现卡尔曼滤波递推算法，设定算法中初始值，根据某时刻的观测值可以计算出该时刻的状态估计值，从而随机扰动误差干扰数据被剔除，消除噪声的影响，实现很好的预测。

1.2 灰色系统理论

1982年我国著名学者邓聚龙教授首次提出了灰色理论(Grey Theory)[7]。该理论是把一个不确定的系统作为研究对象，其中该不确定系统部分信息已知，部分信息未知，主要特点就是“贫样本、贫信息”。通过该系统对“部分”已知信息生成、开发，提取有价值的信息，实现对系统运行规律的正确描述和有效控制[8]。灰色理论模型可以对一个系统对象进行分析和预测，其中预测因子数量决定模型元数，有一阶一元模型GM(1,1)和一阶多元模型GM(1,N)[9]。但是在工程应用领域中，往往采用一阶一元模型，该模型只需要一个单变量。其模型的建立步骤具体如下：

(1)设有n个非负原始观测数据序列X(0)=[x(0)(1),x(0)(2),…,x(0)(n)]，则由X(0)序列累加(1-AGO)得到序列X(1)为:

X(1)=[x(1)(1),x(1)(2),…,x(1)(n)]

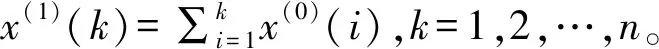
(2)由序列X(1)构造背景值序列Z(1)为:

Z(1)=[z(1)(1),z(1)(2),…，z(1)(n)]

式中,Z(1)取X(1)紧邻均值生成序列，即Z(1)(k)=0.5[x(1)(k)+x(1)(k-1)]，k=2,3,…,n。

(3)建立灰色GM(1,1)模型的一级白化微分方程为:

(8)

式中，a为发展系数，用来控制系统发展事态的大小；b为灰色作用量，用来反映资料变化的关系。

(4)根据最小二乘原理，灰色GM(1,1)模型的参数列为：

A=[a,b]T=(BTB)-1BTY

(9)

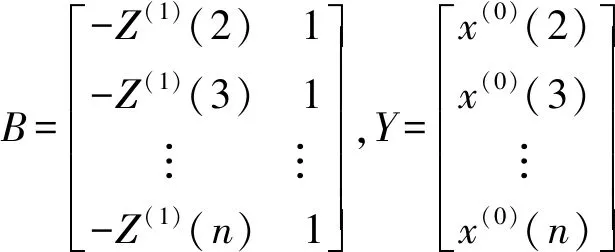
将计算求得的参数a，b带入式(8)，并求解微分方程，取初始条件x(0)(1)，得x(1)的时间响应函数为：

(10)

(5)对式(10)再作一阶累减函数还原计算(1-IAGO)，得到原始序列X(0)的还原值为：

(11)

2 模型的精度检验

2.1 残差检验合格模型

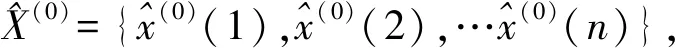
e=[e(1),e(2),…,e(n)]

(12)

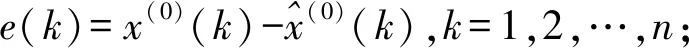
相对误差序列为：

(13)

相对误差Δ表示预测残差占原始数据的比例，呈负相关。

2.2 均方差比与小误差概率合格模型

原始序列X(0)及残差序列e的方差为：

(14)

(15)

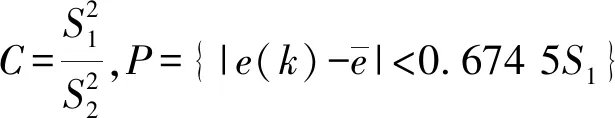
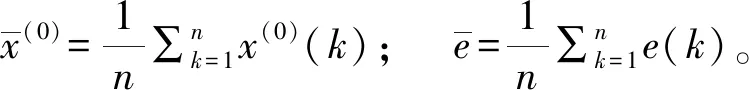
计算后验方差比值C和小误差概率P，模型精度由两个值共同决定，值的大小都是与模型精度呈负相关。

表1 后验差检验法精度等级参照表

3 实例分析

本文以南方某大坝边坡监测点的沉降监测数据为例[10]，来验证基于卡尔曼滤波的GM(1,1)模型对大坝边坡沉降预测的可行性。具体监测数据如表2所示，监测时间是从2013年5月1日开始，观测周期为15 d。

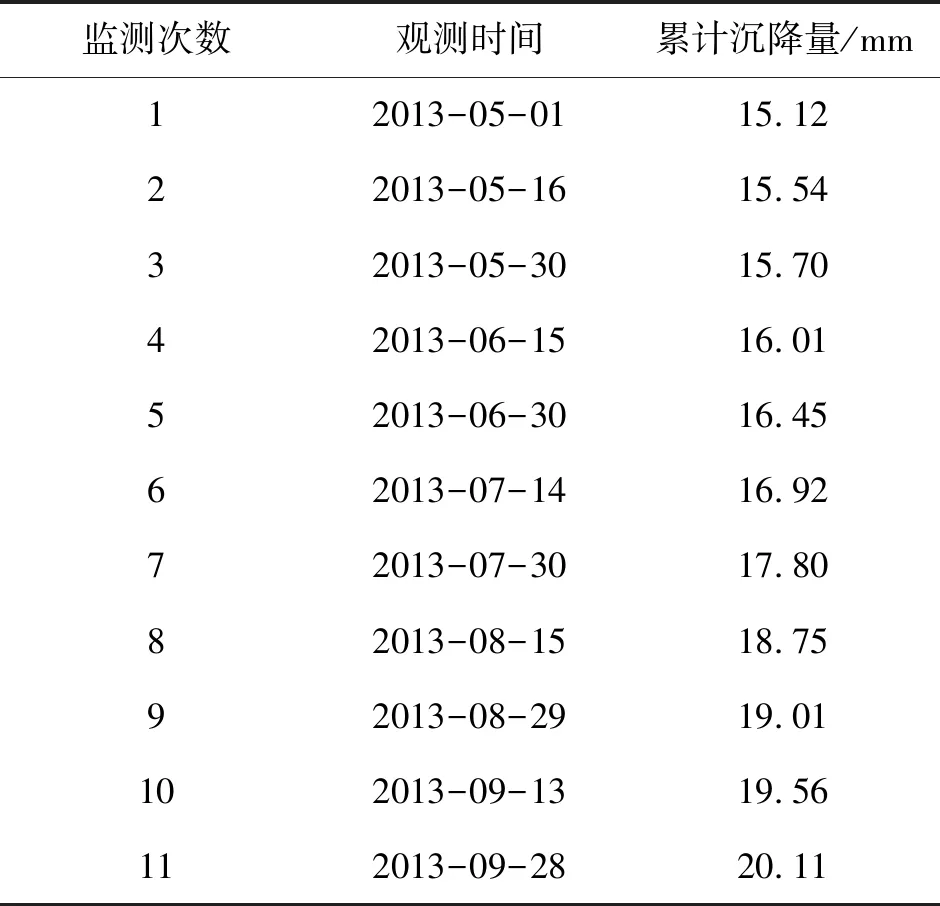
表2 监测点沉降监测

前面分别叙述卡尔曼滤波和GM(1,1)模型的基本原理。把GM(1,1)模型与卡尔曼滤波算法结合，可以有效减弱随机误差干扰。本次实验过程中，选取了前11期监测数据，首先，利用卡尔曼滤波算法对选取的原始数据进行滤波降噪处理，使得原始数据更加平滑；然后，利用滤波处理后的数据建立基于卡尔曼滤波的GM(1,1)模型；最后，把前8期的处理数据作为建模数据，后3期的数据用来验证，并与传统GM(1,1)模型对比分析。

在给大坝进行沉降建模过程中，卡尔曼滤波算法假定监测点的位移速度是一个恒定的值，并且在滤波过程中，把这个恒定的速度和位置作为状态参数，将过程中的加速度认为是唯一的动态噪声[11]。在以往经验情况下，把经验值作为初始参数值Qk、Rk，大小均为1，把监测点的初始位置和变化速率当作状态参数，根据前两期监测值的平差值可求得初始状态向量X0及其相应的方差阵P0，其结果为：

X0=[15.12,0]T

运用MATLAB程序[12]编程执行卡尔曼滤波，对前8期数据进行滤波处理，得到结果如表3所示。

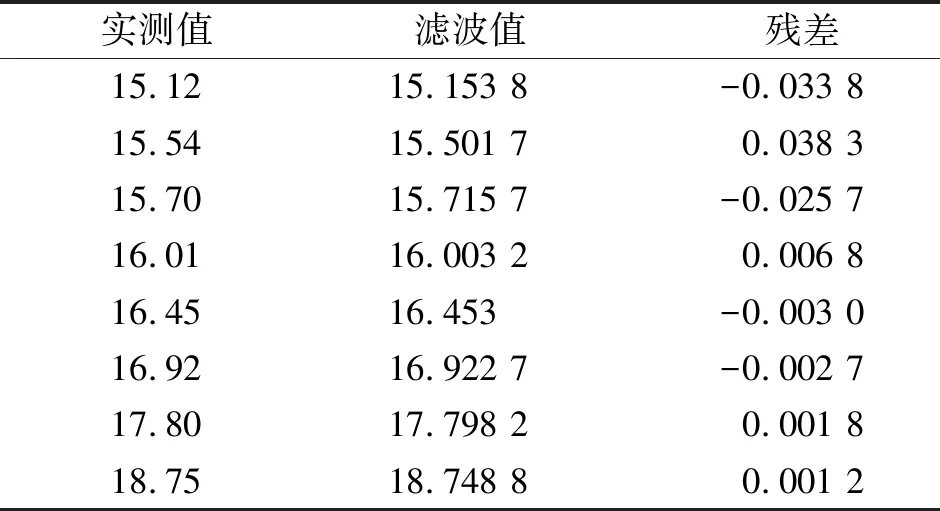
表3 原始数据滤波值/mm

由表3可以看出，残差绝对值从第2期开始收敛于0，由此可以得出原始数据变化范围变小。随机误差得到有效的减弱，在滤波的数据基础上，把滤波数据带入GM(1,1)模型。两种模型对监测数据拟合与预测结果如表4所示。

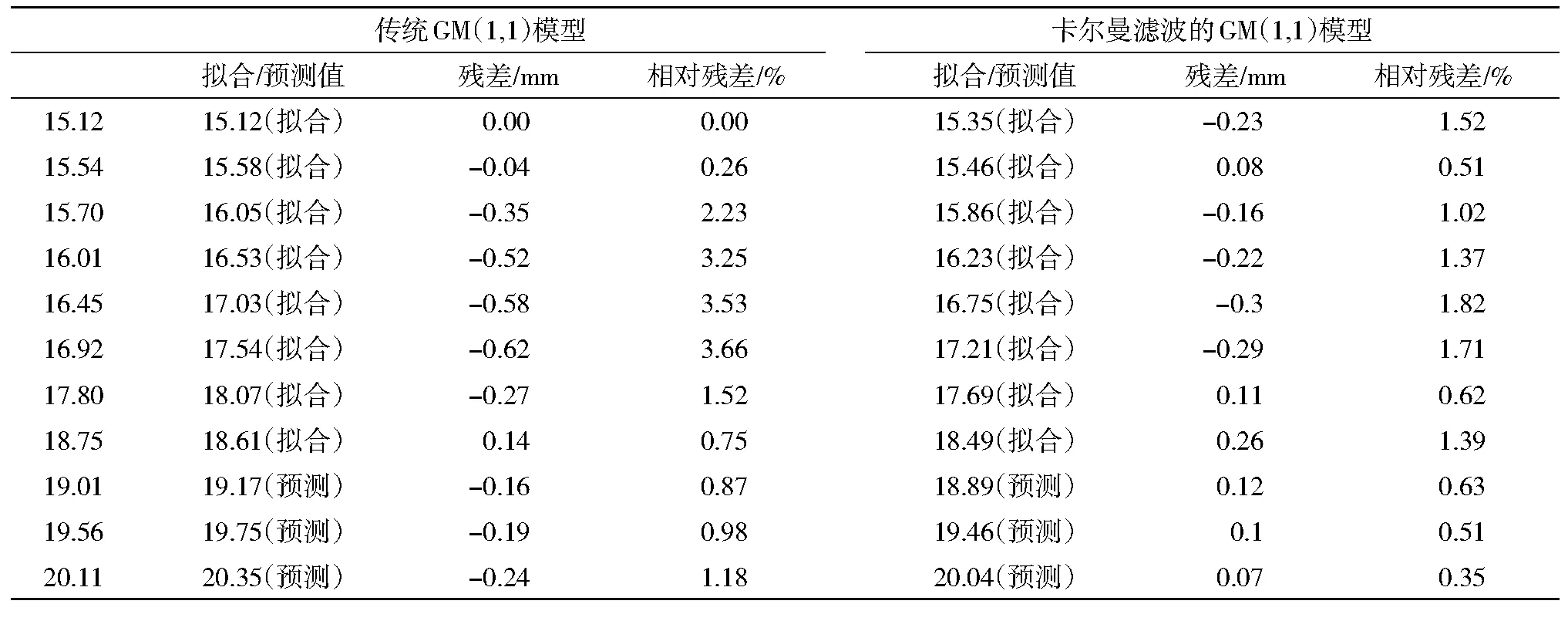
表4 监测点拟合预测结果检验表

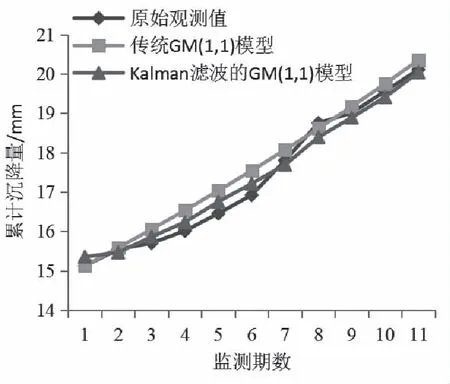
图1 实测值与拟合预测值对比图

由图1分析两种模型可以得出以下结论：(1)通过卡尔曼滤波过后建立的GM(1,1)模型相对于传统的GM(1,1)模型预测曲线较光滑，波动很小。(2)通过卡尔曼滤波过后建立的GM(1,1)模型相对于传统的GM(1,1)模型随着时间的推移，预测值越来越接近实际监测值。

由图2和表4分析两种模型可以得出以下结论：(1)通过卡尔曼滤波过后建立的GM(1,1)模型相对于传统的GM(1,1)模型残差明显减小，在第3

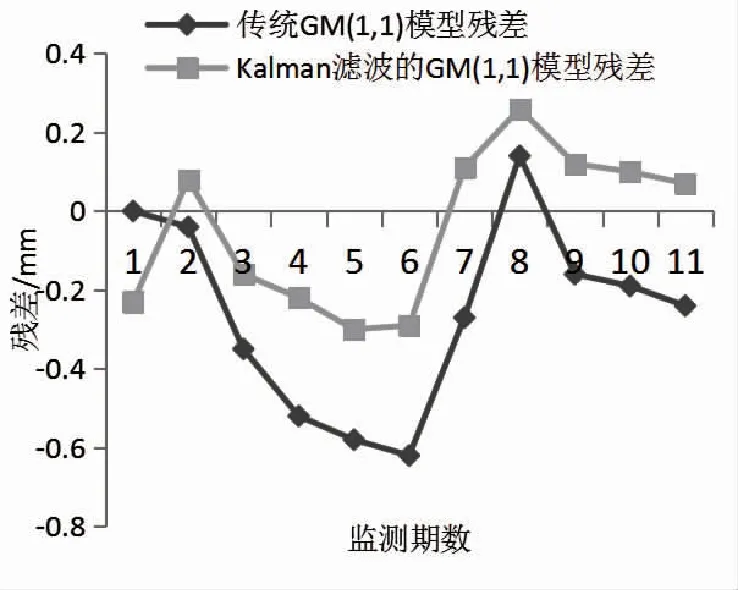
图2 两种模型残差曲线图

～6监测周期中，两模型残差之间的差值越来越大，第8期以后是两模型的临界点，基于卡尔曼滤波的GM(1,1)模型在0值以上，且趋于稳定，而传统GM(1,1)模型残差在0值以下，且有远离0值的趋势。(2)通过卡尔曼滤波过后建立的GM(1,1)模型相对于传统的GM(1,1)模型虽然相对残差基本接近，只有若干点有所减小，但是预测值相对残差大幅度减小。

利用残差合格模型对预测效果进行精度评定，从表4中分析可得监测点传统GM(1,1)模型和基于卡尔曼滤波的GM(1,1)模型平均残差值分别为-0.257 27、-0.041 82，预测精度均为一级。但是，传统GM(1,1)模型的后验方差比值C为0.463 1，而基于卡尔曼滤波的GM(1,1)模型的后验方差为0.219 3，总体精度有大幅度的提高。

4 结 论

本文介绍了卡尔曼滤波算法和灰色GM(1,1)模型，在两种模型基本原理的基础之上，提出建立一种基于卡尔曼滤波的GM(1,1)模型。为了验证该模型的可靠性，采用实际大坝监测数据作为实验验证数据，分别建立两种模型，分析预测结果。最后实验结果表明：(1)基于卡尔曼滤波的GM(1,1)模型相比于传统的GM(1,1)模型预测效果更好。(2)基于卡尔曼滤波的GM(1,1)模型在一定程度上消除了随机误差噪声的干扰，补充了灰色GM(1,1)模型对于趋势项提取的规律性，保留了原始数据的特征，在一定程度上弥补了单一模型的缺陷。由此可见，这种组合模型在大坝变形监测分析中具有较强的适应性。