一种基于局部最优的权系数组合预测模型*

党 升，冯 晓，卢志豪，韦春桃

(1. 重庆交通大学 测绘与国土信息工程系，重庆 400074； 2. 重庆交通大学 工程信息与3S研究所,重庆 400074)

监测数据处理、分析包括数据粗差剔除、滤波去噪、建模预报等，而建模预报是当中非常重要的一部分，其采用的方法一般有回归分析[1]、时间序列[2]、灰色模型[3]、神经网络[4]等。由于某些模型在实际应用中存在一定的不足，有些学者基于原模型提出了相应的优化改进模型，例如稳健回归分析[5]、模糊AR(p)模型[6]、残差修正ARMA模型、小波神经网络[7]模型、改进灰色模型[8]等。为了进一步融合各模型的优点，提高预测精度，又有学者提出建立组合预测模型，例如改进的MEEMD-ARMA残差修正组合预测模型[9]、GM-BP组合模型[10]、灰色-回归组合模型[11]等。

文献[12]在建立最优权组合预测模型时，以全部建模样本的残差平方和作为目标函数，采用最小二乘准则确定多个预测模型的最优权值，从而使组合模型达到基于整个样本数据的全局最优。但由于不同模型的建模原理、建模基准、拟合精度等不同，采用该方法对各个模型进行分权，可能出现权重过度偏向于拟合精度较高的模型而忽略其余模型所特有的隐藏信息，使组合模型的预测精度降低。从系统角度看，随着系统的发展，老数据刻画系统演化的作用将逐渐降低[13]，以此建立的模型并不一定能较好地反应事物发展的真实状况。因此，在对各模型分权时，若能利用近期数据作为权值划分的依据，将一定程度上避免老数据对模型的不利影响。基于此，本文提出一种改进最优的权系数组合预测模型，即基于局部最优的权系数组合预测模型。

1 局部最优的权系数组合预测模型

(1)

为了保证模型的无偏性，wj应满足如下约束条件：

误差统计量为：

(2)

若以最小二乘准则将目标函数极小化来求解权系数矩阵W，则可设：

(3)

式中，j∈(1,J)；t∈(t0,N)且t0∈(1,N)。

组合预测模型的模型误差可表示为：

(4)

(5)

式中，WT=(w1,w2,…，wJ)；RT=(1,1,…，1)；E=(eij)J×J；

若各个预测模型的预测误差是不相关的，则E矩阵可逆，按最小二乘法求得最优权向量为：

W0=(RTE-1R)-1E-1R

(6)

如果上述式中t0=1，所求的权系数即为文献[12]中的最优组合预测模型(整个样本数据的全局最优)。

2 算 例

2.1 精度评价指标

为了验证改进模型在预测中的有效性，本文选用下列几个误差指标作为单项预测模型、最优权系数组合预测模型、局部最优的权系数组合预测模型的精度评价指标[13]：

(4)平均绝对百分比误差：

(5)均方百分比误差：

2.2 EGM(1,1)、三次多项式模型建立

以万州区滨江路某项目的水位监测数据为例，取2018年2月17日～2018年3月16日SW4点的监测数据(28期)，以前22期为建模数据，后6期为模型预测验证数据。

根据文献[14]中记录的方法，建立均值灰色模型(EGM)，得出模型的发展系数a=0.001 616 79，灰色作用量b=170.123 795 2。该模型的时间响应式如下：

-105 223.186)e-0.001 616 79(k-1)

通过MATLAB编程计算，得出基于样本数据的三次多项式模型：

通过建立的EGM(1，1)模型和三次多项式模型，分别计算出各自模型前22期数据的拟合值，经计算，得出EGM(1，1)模型和三次多项式模型拟合值的平均相对误差分别是0.069%和0.012%；同时也对第23～28期值进行预测，最终拟合结果、预测结果如表1～表2所示，拟合、预测值比较图如图1所示。

图1 EGM、三次多项式模型的拟合、预测值比较

表1 EGM(1,1)模型与三次多项式模型拟合值/m

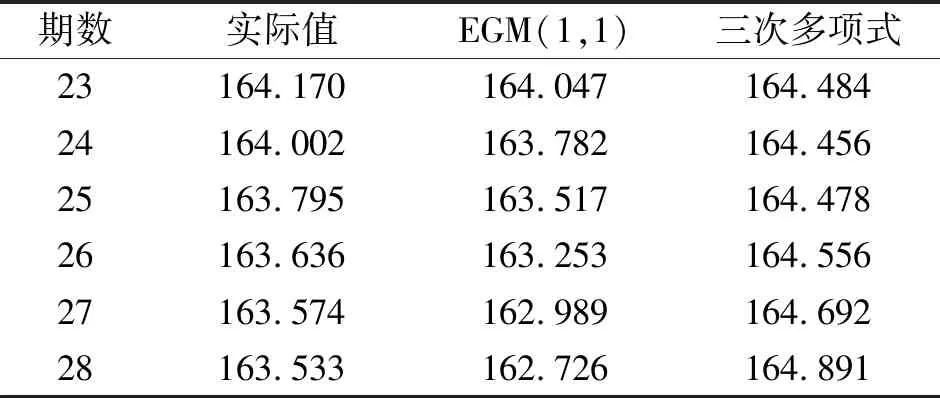
表2 EGM(1,1)模型与三次多项式模型预测值/m

2.3 最优权系数组合预测模型

从图1中可以明显看出EGM(1,1)模型和三次多项式模型后期的预测值均存在部分时域偏离真实值的情况，因此，采用文献[12]介绍的方法(权系数组合预测模型)，对上述两种模型进行分权，得出最优权系数w1,w2，如表3所示。并将两个模型预测值进行分权组合，得出第23～28期组合预测模型的预测值，如表4所示，预测值对比图如图2所示。从上述图表中可以看出，最优权系数组合预测模型的预测趋势与三次多项式模型的大致相当，预测值存在一定偏差，造成该情况的原因是三次多项式模型对原始建模数据的拟合精度远远高于EGM(1,1)，在使用极小化准则分权时过于置信三次多项式模型，导致三次多项式模型权重过大。但仅由模型的拟合精度就过于忽略了EGM(1,1)模型中蕴藏灰色信息，很明显也是不合理的。

表3 最优权系数

表4 权系数组合模型预测值/m

2.4 局部最优权系数组合预测模型

基于2.1章节中所建立的EGM和三次多项式模型，选取第17～22期作为求解局部最优权系数的范围区段。以第17～22期模型拟合值的残差平方和作为目标函数，结合式(5)、(6)可得出局部最优权系数值，如表5所示。

图2 三种模型预测值比较

表5 局部最优权系数

应用式(1)，将EGM和三次多项式模型进行加权组合，经计算可得到第23～28期的局部最优权系数组合预测值，如表6所示,各模型预测值对比图如图3所示。根据预测精度评价指标体系对单项模型、最优权系数组合模型、局部最优权系数组合模型进行评价，如表7所示，可以看出最优权系数组合模型的指标均高于单项预测模型，这也表现了组合模型在预测中的优越性。根据表7和图3可以看出局部最优的权系数组合预测模型的预测值较为符合真实值变化趋势，预测评价指标在各方面均优于单项预测模型和原组合模型，预测精度有了较大的提升。

表6 局部最优权系数组合模型预测值/m

3 结 语

本文基于EGM(1，1)和三次多项式模型，针对最优权系数组合预测模型存在的问题，提出一种基于局部最优的权系数组合预测模型的计算方法。通过建立最优权系数组合预测模型和局部最优的权系数组合预测模型，得到第23～28期水位的预测值，与测量值对比后，分析总结得出：

图3 局部最优权系数组合模型预测值比较

表7 预测评价指标

组合模型可以充分考虑各模型的不同特性和优点，当多个单项预测模型拟合值的平均相对误差存在相对较大差异时，采用最优组合预测模型(基于全部样本数据的最优)进行分权时，会导致偏权情况。基于局部最优的权系数组合预测模型以t0～N时刻各个预测模型的残差平方和为目标函数，通过最小二乘准则确定模型在t0～N时刻的最优权，并将该权作为组合模型的权值，在处理时很大程度上保护了拟合精度较低模型的灰色信息，提高组合模型精度。在短期预测中，改进权系数组合预测模型的效果与权系数组合预测模型相当，但在中长期预测中，局部最优的权系数组合预测模型的预测精度和趋势明显优于原模型。