基于声学法的磨煤机入口冷热混合风风速测量研究

储 墨，杨柏依，赵 亮，杨伟山，周 宾

（1.华能莱芜发电有限公司，山东 济南 271100；2.东南大学，江苏 南京 210096）

0 引言

风速的准确监测对磨煤机效率的提高和燃烧优化具有非常重要的指导和参考意义［1］。目前，国内燃煤机组常用的测速方法有矩阵皮托管［2］、光学信号互相关法［3］、PIV图像粒子测速［4］和射线离子测速［5］等。在现场测试中存在修正系数不稳定、易堵塞、磨损和单点测试不具代表性的问题；同时，矩阵皮托管测量装置的测量点数对流速的计算结果会产生一定的影响；测点的空间分布方式对流场干扰的影响比较大。

声学法风速测量对流场干扰小或几乎无干扰，不会存在堵塞和定期修正的问题，由于设备通过导管导出声波进行测试，所以对设备几乎无磨损。安连锁等［6-10］对声音信号的选择以及提高声波飞渡时间精度等进行了深入研究。沈国清［11］采用声波信号互相关方法验证了采用声学法进行气体流速测量的可行性。陈栋［12］对声波测速装置进行了改进，研究了声学测点布置角度对测量灵敏度的影响，提高了声波测速的灵敏度。

利用声学法对磨煤机冷热风混合风量测量的研究报道较少，因此，通过对不同温度下的声波在磨煤机入口冷热混合风道中的传播情况进行仿真，得到流场中各影响因素与流速的关系。通过声学法得到冷热混合风的平均流速，最终实现声学法风速测量系统的研发，形成风速测量的优化方案。

1 磨煤机入口风速声学测量原理及时延估计

1.1 磨煤机入口风速声学测量原理

声波在磨煤机冷热混和风中的传播主要受到风温和流速的影响。通过空气静止区域的风温可以求得声速

式中：c 为声波在静止空气中的传播速度，m／s；γ为介质比热容比，与介质成分有关；R 为气体常数，J／（mol·K）；T 为热力学温度，K；M 为介质摩尔质量，kg／mol。

声学测速技术作为一种非侵入式测量方法，通过利用声波在待测区域的飞行时间和测量位置得到气体介质的流速信息［13］。

声波在冷热混合风中的实际传播速度等于风速与声波在静止空气中的传播速度的叠加，如图1 所示。在介质流向的顺流、逆流两个方向上各布置一组扬声器和传声器，通过获取声波在两个方向上的声波飞渡时间以获取介质流速。

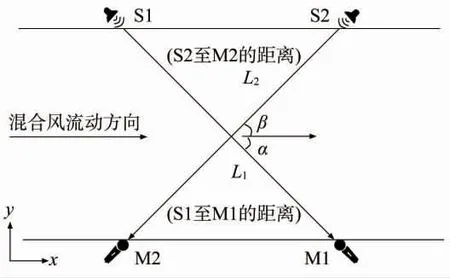
图1 磨煤机混合风声波测速原理

顺流和逆流方向的扬声器和传声器均固定在声波导管内部，声波导管后部为封闭状态，扬声器S1发射声波信号，由于声波顺风传播，声波飞渡到传声器M1 所用的时间为τ1；之后，当扬声器S2 发射声波信号时，由于声波逆风传播，声波飞渡到传声器M2所用的时间为τ2（τ1<τ2），则声波在L1的飞渡时间τ1可表示为

同理，在L2的飞渡时间τ2可表示为

由式（2）和（3）可知，气体流速为

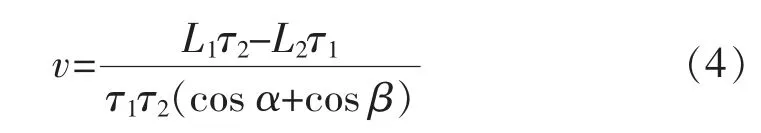
同时可得声速为

式中：τ1、τ2为声波在顺流及逆流方向上的飞渡时间；L1、L2为顺流及逆流方向的声线长度；α、β 为顺流及逆流方向传感器的安装角度。

1.2 互相关时延估计

式（5）中飞渡时间τ1、τ2可通过直接互相关算法得到，信号延迟时间的准确估计是准确计算风速的关键。互相关时延估计是比较两个相对独立时间序列信号的相关程度，通过计算两信号之间的偏移点得到相对应的声波飞渡时间。

假设x1（n）和x2（n）分别表示扬声器发射信号和麦克风接收信号，s（n）表示声源信号，μ1（n）和μ2（n）表示信号采集时的随机噪声，γ 表示声波信号衰减系数，D 表示声波发射方向上的时间延迟，其数学模型可表示为：

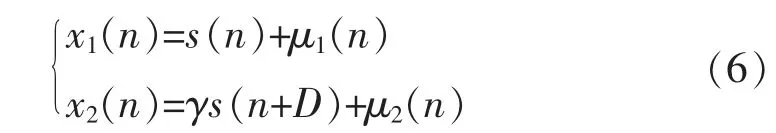
x1（n）和x2（n）的互相关函数可表示为

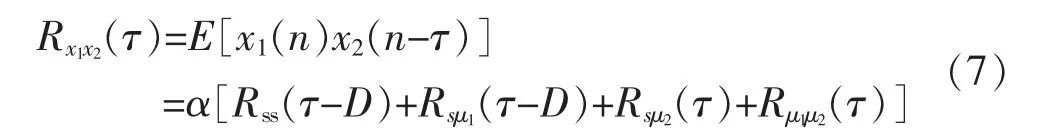
式中：Rss为声源信号s（n）的自相关函数；Rsμ1和Rsμ2为声源信号与随机噪声信号的互相关函数；Rμ1μ2为两路随机噪声的互相关函数；α 为声吸收系数。假设s（n）、μ1（n）和μ2（n）为不相关的随机信号，则

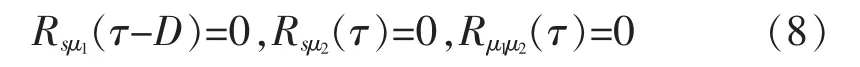
公式（7）可简化为

由式（9）可以看出，飞渡时间时延估计通过声源信号的自相关函数得到。其中，飞渡时间时延估计受到声波衰减系数变化的影响。

2 数值仿真结果与分析

由于现场实验和实验室实验为同样的扬声器，其声源辐射的波形、声束等声源特性相同，辐射衰减与风道中空气介质无关，所以仿真只考虑吸收衰减，忽略扩散衰减。根据文献［7-10］的研究，采用线性扫频声源信号对高温风道中的声波衰减情况进行仿真研究。

2.1 背景噪声分析

图2 为风道背景噪声频谱快速傅里叶变换（Fast Fourier Transform，FFT）分析。由图2 可知，背景噪声的频率主要低于3 500 Hz，为了避免背景噪声对监测过程的干扰，声源信号的起始频率要与背景噪声的主要频段不同，即要大于3 500 Hz，使采集信号中的噪声频段比重最低。

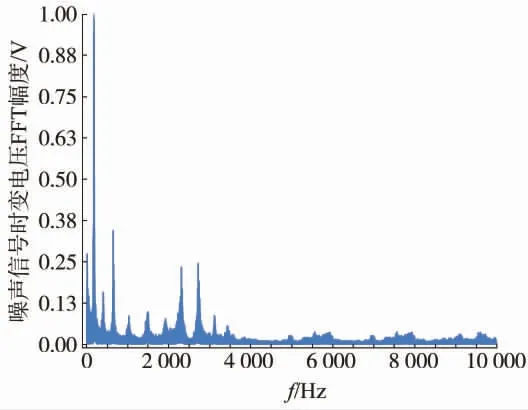
图2 风道背景噪声频谱分析

2.2 声波在风道中的吸收衰减

声波在理想介质中传播时，不存在任何能量的耗散，即传播介质对声波没有吸收作用。但是由于磨煤机入口风道中存在冷热混合风，声波的传递过程是非理想状态，随着传播距离的增大，部分声波能量转变成热能进行耗散，使声信号发生了衰减［14］。声波在传播过程中，混合空气介质存在粘滞性，对声波产生吸收作用，这是声波在风道中传播时衰减的主要原因。声波在经过气体介质时，气体产生压缩和膨胀的变化，压缩部分体积减小，导致温度升高，膨胀区域体积变大，导致温度降低。由于理想气体此过程为可逆过程，所以不考虑介质对声波的吸收作用，但是磨煤机入口风道中冷热混合风为非理想介质，相邻的压缩区域和膨胀区域的温度梯度会导致热量由高温区域流向低温区域，此热传导过程是不可逆过程，导致机械能转化为热能，从而引起声波吸收［15］。

由经典公式可得介质的热传导吸收系数为：

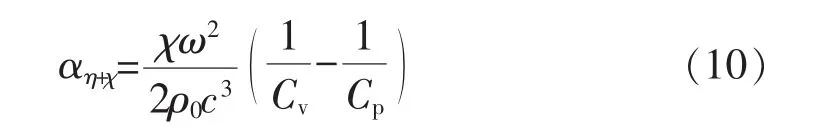
在考虑黏滞声吸收和热传导声吸收后，总的声吸收系数为

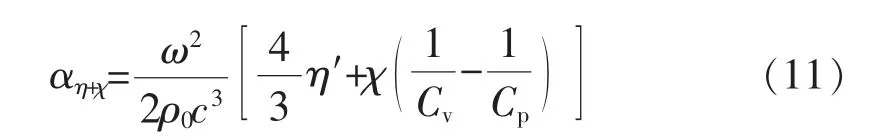
式中：χ 为热传导系数；Cv为定容比热容；Cp为 定压比热容；ω 为声波角频率；ρ0为介质密度；η′为切变黏滞系数。

由式（11）可知，声波黏滞吸收系数与热传导吸收系数均和角频率平方成正比，随着频率的增加，黏滞衰减系数平方增大，声波衰减越严重，根据文献［6-7］的研究及风道背景噪声的频率分布，确定仿真频率采用4～8 kHz。

2.3 低信噪比下相关性仿真分析

由于测量环境中存在大量加性噪声，且不同测量环境下其噪声能量不同。对于电厂磨煤机入口冷热混合风道环境中，噪声的主要成分为高斯白噪声［16］，通过对衰减、时延后的声源信号添加不同信噪比的高斯白噪声仿真分析声源抗噪能力。

仿真中，声源信号扫描频率范围为4～7 kHz，有效信号时长为0.2 s，占空比为0.2，设置接收信号时延为20 ms，对信噪比 （Signal-to-Noise Ratio，SNR）从-20～0 范围进行仿真，每个数据的计算次数200次。

图3 SNR 为-7 时的接收信号

图3 为SNR 为-7 时的接收信号，从图7 中可以看出，其信号波形在低信噪比下仍能够区分，但是时延估计情况并不能通过信号波形看出。

图4 为不同信噪比下信号的相关性，相关性越大则时延越准确。相关函数图像的横坐标为SNR，随着信噪比的降低，声源信号与时延信号间的相关性逐渐减小。

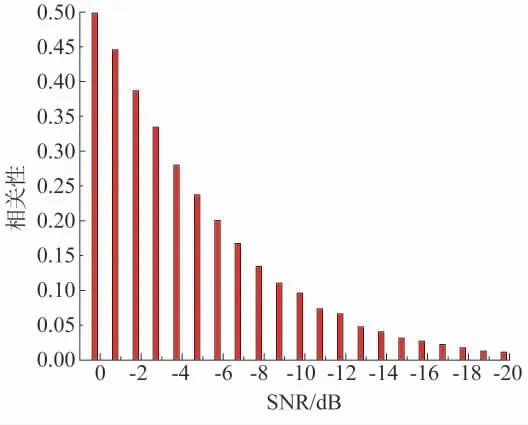
图4 不同信噪比下信号相关性

由图4 可知，随着信噪比的降低，声源信号与时延信号的相关性逐渐降低，在SNR 低于-15 dB 后，相关性降低幅度减小。根据对电厂环境的背景噪声进行分析可知，风道内部时延信号的SNR 约为-6.78 dB，由图4 可知，在测试环境中仍然能有较高的信号相关性，声学互相关算法可以在现场环境中进行应用。

3 现场实验

3.1 实验介绍

本项目以华能莱芜电厂1 000 MW 超超临界二次再热机组工程为依托。

声波测速设备安装于6 号炉E 磨煤机入口冷热风混合管道，风道截面直径为1.70 m 的圆形管道，通过气动隔绝门的阀门控制及调节进风量及混合风量，在磨煤机入口位置安装皮托管进行监测，并与声波测速结果进行对比。扬声器及传声器均布置在流道两侧。其安装结构如图5、图6 所示。

3.2 传感器距离标定

扬声器及传声器安装完成后，由于其均与流道成一定角度，传感器间的准确距离很难通过常规测量手段得到。通过声波飞渡时间标定出传感器间的准确距离，在安装完成后，风道内无气体流动，此时，扬声器所发射的声波信号不受流速干扰，且温度几乎不变，其声速c 为定值。经过静止状态下的声音传播速度的多次测量求得平均值，可得静止时声速c为338.640 m／s，顺、逆流的扬声器与传声器距离分别是2.344 9 m 和2.418 1 m，顺、逆流声线与管道的安装角分别为45.93°和46.77°。

图6 传声器端安装结构

3.3 实验结果与分析

实验过程中，环境温度会有轻微波动，平均在260 ℃左右，声速在495.64 m／s 左右波动。设置采样频率为500 kHz，声波测速的系统响应时间约为1.5 s。图7 为磨煤机冷热风混合后的测速结果，测试周期约为20 天。从图7 中可以看出，声学法与皮托管测速结果基本吻合测试曲线基本吻合，声学法测速结果相较于皮托管略大。由于皮托管为压差式测量，其速度结果的响应能力较差，对速度波动不灵敏。由于距离送风机较近，流场波动较大，从声波测速结果中可以明显看出速度的波动及变化情况。

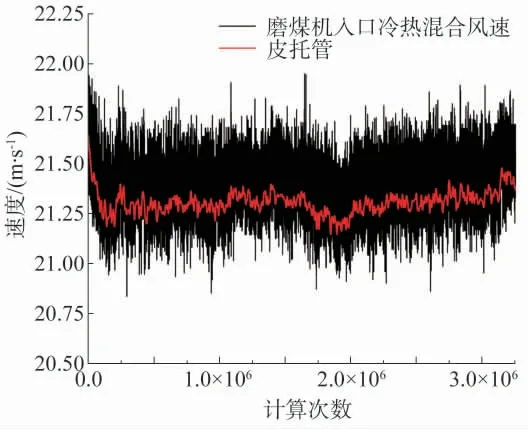
图7 声学测速及皮托管测速结果

4 结语

不同温度下的声波在风道中的传播情况进行仿真，得到流场中各影响因素与冷热混合风流速的关系。磨煤机入口冷热混合风对声波的衰减影响较小，并不影响声波互相关算法计算气体流速。

根据风道内部背景噪声及仿真分析，确定声学测速中的声源信号频段为4～7 kHz，能够与噪声频段隔离。

声学磨煤机冷热风混合风量测量能够在不影响管道流场的情况下准确测量混合风流速，而且能够方便安装及更换传感器，传感器本身不会受到冷热混合风的磨损，能够做到长期稳定监测。