结构性软土地层中后掘进隧道引起地表沉降计算模型分析

高坤，柯宅邦，童智能，陈小川

（1.安徽省建筑科学研究设计院绿色建筑与装配式建造安徽省重点实验室，安徽 合肥 230031；2.安徽省建筑工程质量第二监督检测站，安徽 合肥 2300031；3.江西科技师范大学建筑工程学院，江西 南昌 330013）

1 引言

盾构法隧道是目前较为先进的地铁隧道施工方法，广泛应用于城市地铁隧道修建。尽管盾构施工对环境影响较小，但仍不可避免扰动邻近土体，从而影响到邻近构筑物的安全使用。评价隧道施工对邻近构筑物的影响是城市隧道施工的一个重要课题，而合理预测邻近结构物安全性的基础在于准确预估隧道施工引起的位移。

目前国内外众多专家学者提出预测隧道施工引起的地层位移方法[1-6]。其中，应用最为广泛的为Peck高斯公式[1]及Loganathan and Poulos[6]法。伊利诺伊州大学Peck教授在收集大量的隧道位移数据后指出，隧道施工引起的地表位移可以通过高斯分布曲线拟合[1]。西悉尼大学教授Loganathan and Poulos[6]在Verruijt and Booker[5]基本解基础上，重新定义土体损失率，考虑隧道不均匀收敛的情况，提出预测隧道横向及深层位移的解析解。该解法被广泛应用于求解隧道施工对邻近桩基影响的“两阶段解法”中[7,8]。

上述研究成果基本集中于单线隧道施工地表沉降位移分析，对于双线隧道施工引起地表沉降的研究较少。而在结构性地层中，先掘隧道对后掘隧道地表沉降的影响不可忽视。结构性软黏土层中盾构施工扰动邻近土体，特别已破坏土体遭受后掘隧道施工的再次扰动，土体强度急剧下降[9]，地表沉降规律与单隧道沉降明显不同。图1给出在宁波地铁一号线区间结构性地层中，先、后掘隧道掘进引起地表沉降的典型位移图。

图1 宁波地铁一号典型隧道施工引起的地表沉降曲线

由图1可见，在结构性地层中，先掘进隧道引起的地表位移符合正态分布，可通过文献[1,2]提出的方法拟合。而后掘进隧道引起地表沉降曲线与先掘隧道相比明显不一致，位移曲线呈现“双沉降槽”形态，两沉降峰值点分别位于两隧道轴线处，并且先掘隧道处最大沉降大于后掘隧道。究其原因，宁波地铁一号线所在地层为灵敏度高的结构地层。在此类地层中先行盾构掘进引起地层扰动，破坏土体的结构性，而后续平行隧道在已遭受结构性破坏的地层中施工，再次引起地层沉降，特别是靠近先行隧道一侧的沉降更为明显，导致地表沉降不均匀对称分布，甚至出现先行隧道一侧沉降大于后掘隧道的现象。而目前的地表预测方法基本不考虑先掘隧道的扰动影响，难以准确反映现场工程实测。因此，提出一种考虑结构性扰动的地表沉降预测公式十分必要。

本文提出一种考虑先掘进隧道扰动效应的后掘进隧道地表沉降预测方法。该方法认为后掘进隧道引起的地表沉降S可分为两部分：①正常掘进引起地表沉降Sn；②由于扰动引起的额外地表沉降Sa。该方法假定，后掘进引起的额外沉降Sa亦可用Peck高斯公式预测。叠加正常地层中盾构施工引起的地表沉降值Sn，即可得到后掘进隧道在已扰动地层中施工引起的地表沉降位移S。本文计算方法简单，参数意义明确，便于工程实际应用。

2 双线盾构隧道掘进相互作用机理

在稳定状态的地层中，盾构掘进将引起地层周围初始应力状态发生改变，邻近土体发生加载、卸载、剪切或挤压等复杂的力学行为，原始稳定平衡状态被打破，土体遭受扰动，从而引起地层变形。不同位置处土体经历的扰动程度与应力历史不尽相同。易宏伟等[10]、房营光等[11]和魏纲等[12]根据盾构（顶管）施工土体受力特性，分别提出定性邻近土体扰动分区模型。综合前人的研究，不同相对位置的土体扰动具有如下规律：位于盾构前方土体受到刀盘切削和千斤顶挤推作用，土体经历压缩、挤压及剪切等一系列复杂力学作用，扰动程度激烈；在盾构体周围邻近土体，遭受盾构侧摩阻力剪切作用，于盾体周围形成剪切扰动区；在盾尾部土体，由于盾尾间隙的存在及土体超挖的作用，引起盾尾土体松动，应力释放，土体向管片位移。与此同时，同步注浆压力又对松动土体产生挤压，导致盾尾土体经历先释放再挤压的复杂应力变化。盾构通过后，受扰动土体的变形模量降低、孔隙水增加、密实度变差、承载力下降以及渗透性受影响。而对于灵敏度较高的土体，盾构推挤效应造成的不利影响将更加明显。

上述定性分析盾构掘进扰动分区，在实际工程中，定量考察邻近土体扰动程度尤为重要。徐永福等[13]指出盾构掘进引起附近超土体孔隙水压力，导致土体的有效应力下降，并提出扰动比R表征盾构掘进前后土体受扰动的程度：

式中σ'd是受盾构掘进影响后的土体的有效应力，σ'0是土体的原位有效应力。

张庆贺等[14,15]对上海地铁二号线某区间盾构掘进前后邻近土体进行静力触探试验，试验结果表明，在盾构掘进过后，邻近土体受扰动，锥尖阻力明显下降。王斌等[16]对穿越路堤的顶管施工进行扰动试验研究，实验结果表明，顶管穿越前后土体锥尖阻力降低，压缩系数增大，孔隙比增加，塑性指数增大，液性指数减小。白云等[17]对上海7号线实测发现，当后掘进隧道超越先掘隧道后，地表沉降呈现不对称形态，靠近超越隧道一侧的沉降略大。

综上所述，在盾构（顶管）掘进过程中，盾构刀盘挤压、剪切前方土体，土体经历加载、卸载等复杂的应力行为，邻近土体受不同程度的扰动。特别是在天然结构性软黏土地层中，经两次扰动后土体原始结构被破坏，土体承载能力、强度明显下降，导致后掘进隧道地表沉降特性有别于传统单隧道沉降。在现场通常采用静力触探等原位试验手段，进行定量测试土体强度变化，分析盾构通过前后邻近土体扰动程度。

3 双线盾构掘进后掘进隧道地表沉降计算模型

为反映结构性地层中，后掘进隧道的地表沉降特征，本文提出考虑先掘进施工扰动影响的后掘进隧道地表沉降预测计算模型。

双线隧道在结构性软土地层中施工，后掘进隧道引起的地表沉降规律与单隧道施工不一致，地表沉降往往呈现“双沉降槽”不对称分布。为反映这一规律，本文假定：后掘进隧道施工引起的地表沉降可由如下两部分叠加：①原始地层中盾构引起的地表位移Sn（可用高斯分布拟合），叠加②受扰动结构性地层中额外的地表沉降Sa。后掘进隧道地表沉降模型如图2所示。

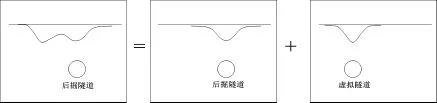
图2 后掘进隧道引起地表沉降预测模型示意图

原始地层隧道掘进引起的地表位移，可通过高斯分布曲线拟合[1,2]：

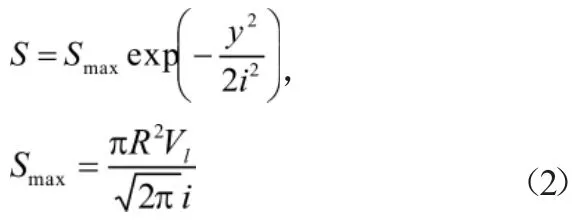
式（2）可转化为：

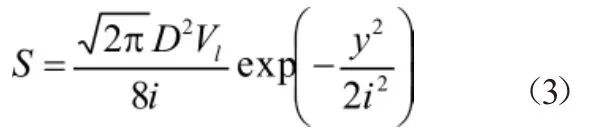
式中：i=k0z[40]，S 为地表位移（mm）；Smax是地表轴线处最大位移（mm）；y为到轴线的距离（m）；i为隧道轴线到反弯点的距离（m）；z为隧道埋深（m）；Vl为土体损失率（无量纲）；D为隧道直径（m）；k0为沉降槽宽度系数；对于粘性土取 0.4～0.7，砂性土取值为 0.2～0.3[40]。

额外的地表沉降Sa计算如下。假定位于先掘隧道位置处有一相同直径的虚拟隧道掘进，引起的地表沉降为受扰动结构性地层中额外的地表沉降Sa，Sa亦可用高斯分布曲线描述。则后掘进隧道引起的地表沉降计算公式如下：

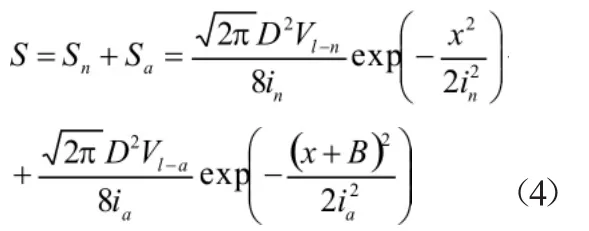
式中，V1-n与Vl-n分别为正常掘进与虚拟隧道掘进引起的土体损失率；in与ia分别为正常掘进与虚拟掘进隧道地表沉降槽宽度；B为两隧道的间距，当B≤H+R，先掘隧道对后掘隧道地表沉降影响较大；当B＞H+R，先掘隧道对后掘隧道地表沉降影响较小，可按正常隧道地表沉降计算[18]。

因而，在扰动地层中，后掘隧道引起的额外沉降效应通过虚拟隧道施工实现。值得注意的是，虚拟隧道掘进引起Vl-a，ia的取值不同于正常隧道施工引起的土体损失率及沉降槽宽度，其取值与扰动程度及土体灵敏度有直接关系。

4 结论

本文提出了一种可以考虑先掘隧道影响的结构性地层后掘进隧道沉降预测方法。该方法通过引进虚拟隧道施工来考虑结构性地层中先掘隧道的扰动影响，并认为虚拟隧道施工与正常后掘进隧道施工均可通过常用的高斯分布公式计算，两者叠加便得到在结构性地层中后掘进隧道施工引起的地表沉降曲线，为城市轨道交通建设提供了理论支撑。