基于区域插值的视差图平滑算法及三维重建

田婷婷,高瑞贞,张京军

河北工程大学机械与装备工程学院,河北 邯郸 056038

三维重建在移动机器人自主导航系统、航空及遥感测量、工业自动化系统、虚拟现实以及医疗诊断等各个领域有着广阔的应用前景[1]。目前，三维重建方法主要有三种。(1)利用建模软件进行手工重建。通过三维CAD、3DMax 等软件进行三维重建，需要预先确定建模对象在重建场景中的位置姿态、尺寸大小和纹理特征等信息[2]。(2)利用深度扫描仪、激光器、雷达等设备来进行三维重建。这种方法自动获取对象建模信息，数据比较精确，但相关设备昂贵，不易携带。(3)利用图像进行三维重建。通过对单张图像(单目立体视觉)或多张图像(双目立体视觉或者多目立体视觉)进行特征检测与匹配，获得深度信息进行三维重建。单目立体视觉需要提取特征数据，因而过程繁琐。双目立体视觉通过立体匹配获得视差图，根据视差图计算出物体的三维坐标，进而实现三维重建[3,4]。

立体匹配是双目立体视觉的关键步骤，易受遮挡、视差间断等因素影响，导致在视差图中存在较多的误匹配区域[5]。改善视差图的方法主要有两种：一种是优化立体匹配算法，能获得较好的视差图[6]。Hoc DK,et al.[7]通过修改SAD(Sum of Absolute Differences)算法，利用感兴趣像素的边缘像素估计视差值的差异，计算深度图信息，具有减少像素的搜索数量、节省匹配时间和提高匹配效率等优点。Hamzah RA,et al.[8]提出了高精度三维表面重建立体匹配算法，获得了较高的匹配效率，同时有效抵抗了辐射度差异和边缘失真。另一种方法是对视差图进行后处理，直观反映立体匹配效果。Chao Z,et al.[9]利用灰度直方图对左右视图处理，使左右视图灰度值近似，提高立体匹配的准确性，获得比较连续的视差图。Nieradka G,et al.[10]首先对视差图进行边缘检测获得边缘图像，其次进行均匀性计算确定均匀性图像，再次根据边缘图像和均匀性图像采用形态学操作确定误匹配区域，然后使用模糊中值算法去除误匹配区域，最后利用拉普拉斯插值算法对视差图增强。为了有效地进行误匹配区域的判别和消除，李从利等[11]结合序列图像拼接的匹配算法，给出了基于同名区域面积差、区域重心同位、区域重心距离比及配准参数复用四种误匹配区域的消除方法。赵春晖等[12]利用基于特征点主方向的尺度信息的统计优化方法来消除误匹配，该算法对图像的旋转和缩放变换具有良好的鲁棒性，对于具有重复结构的图像匹配效果也较好。

综上所述，视差图中的误匹配区域直接影响三维重建效果，本文提出一种视差图后处理优化算法，用于消除误匹配区域获得平滑的视差图，进而实现良好的三维重建。文中首先采用标准数据集中的图像对进行立体匹配得到视差图；其次采用基于区域的插值算法去除误匹配；然后采用三角网格线性插值算法对视差图进行填补；最后根据三角测量原理进行三维重建，实验结果表明本文所提算法能够较好地实现三维重建。

1 立体匹配

根据视差图中匹配点对的数量划分，主要分为稠密匹配和稀疏匹配[13]。稀疏匹配是特征匹配的自然延伸，针对一些特征点恢复其三维空间坐标，获得的视差图比较稀疏，有效信息较少，不利于重建三维结构。而稠密匹配则恢复图像中每一个像素点的空间坐标，与稀疏匹配方法相比可获得较好的视差图[14]。

立体匹配过程如图1 所示。在左侧图像中，(Lu，Lv)处的像素对应于右侧图像中(Lu-d，Lv)处的像素，其中d∈[dmin,dmax]表示匹配像素的搜索范围，为了可靠获得左侧图像中选定像素在右侧图像中的对应点，需要创建一个关于选定像素的模板匹配区域T，其大小设置为W×W。水平移动模板匹配区域T穿过右侧图像。与模板匹配区域T最为相似的那个位置就是对应点，从而计算出视差值。由于图像对之间的尺度和姿态固定不变，采用此方法可以减小搜索范围，提高匹配效率。

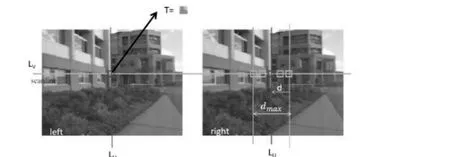
图1 立体匹配Fig.1 Stereo matching

在模板匹配过程中，常用零均值归一化互相关算法(Zero-mean normalized cross-correlation,ZNCC)，进行相似性判断。ZNCC 计算式如下：

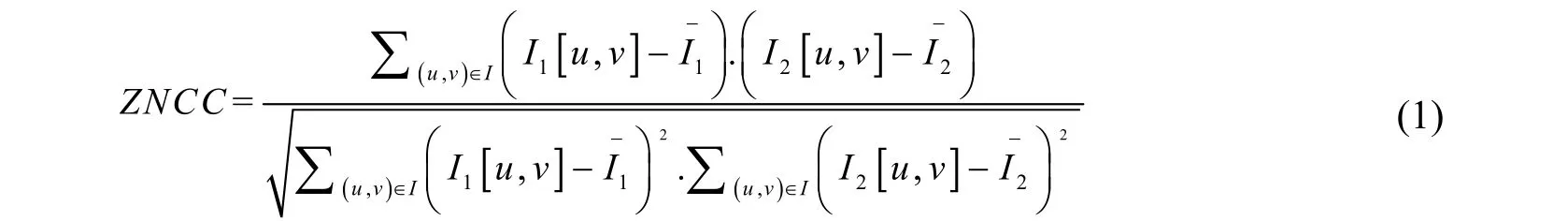
其中，I1[u,v]和I2[u,v]分别为左右图像对应匹配区域的中心点像素，I-1和I-2分别是左右图像对应匹配区域的像素平均值。

ZNCC 取值在[-1,1]之间，1 表示左右图像匹配区域完全相同，-1 表示左右图像匹配区域完全不同，通常认为，ZNCC 值大于0.8 的区域匹配是良好匹配[15]。以标准数据集Middlebury[16]中的Bowling1图像对和Rocks1 图像对如图2 所示为例，进行立体匹配，剔除ZNCC 值小于0.8 的不良匹配区域，获得视差图如图3 所示。

图3 视差图显示，物体的连接处有明显的不连续现象，并且伴有较多明亮点。这些亮点一般是误匹配区域，导致三维重建效果较差。

图2 标准图像对Fig.2 Standard image pair

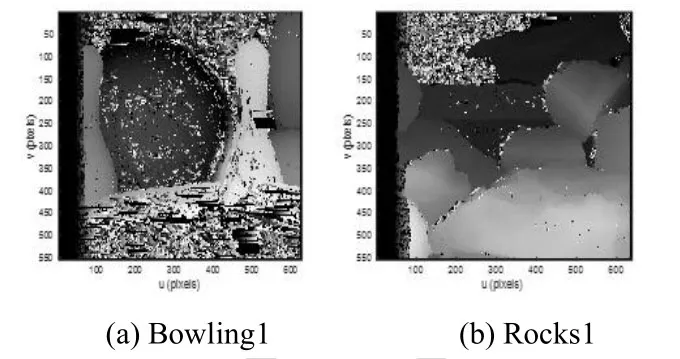
图3 视差图Fig.3 Disparity map

2 视差图后处理

插值方法能够对视差图像素值进行插补[17]，预估视差图特定区域的像素值，平滑视差图，消除误匹配区域。本节采用基于区域的插值算法和三角网格线性插值算法对视差图进行后处理。

2.1 基于区域的插值算法

在图像处理中，插值算法主要有双线性插值和双三次插值[18]。双线性插值对待插值点周围相邻的4 个像素点进行插值计算，得出待插值点的像素值，插值公式如下：

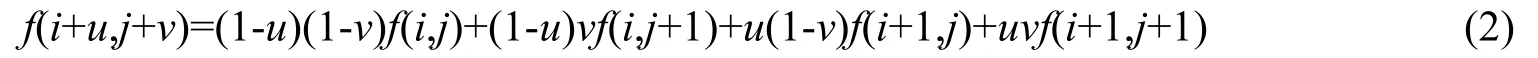
其中，i、j均为非负整数；f(i+u,j+v)表示待插值点像素；f(i,j)表示在原图像中(i,j)位置像素点的像素值；u、v均为[0,1)区间的浮点数，分别表示待插值点与最邻近像素点在水平和竖直方向的距离。双三次插值又称立方卷积插值，插值函数计算公式为：

其中，I(X,Y)表示待插值点像素；aij(i,j=0,1,2,3)表示距离I 最近的16 个像素位置；W(i)，W(j)分别表示横纵坐标的权重。

与双线性插值相比，双三次插值利用采样点周围16 个点的灰度值做三次插值，不仅考虑到4 个直接相邻点的灰度影响，而且还考虑到各个邻点间的灰度值变化率的影响。

由于双三次插值要对周围16 个相邻的插值点做插值，如果要对整幅图像的像素均采用同样的算法，计算量会很大。为了减少计算量，考虑到图像在比较平坦的区域像素值变化较小，在这部分区域可以采用双线性插值算法，在像素变化明显的区域采用双三次插值算法，这样可以在减小计算量的同时得到较好的视差图。鉴于此，本节采用基于区域的插值算法，即定义一个阈值T，利用阈值T对图像进行区域划分。首先计算待插值点周围4 个领域点的方差D，方差D的计算公式为：

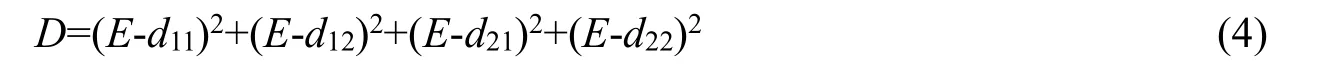
其中，d11、d12、d21、d22分别为待插值点在原图像中对应点的领域4 点的视差值；E表示该4 个点视差值的均值。

如果计算所得方差D小于设定的阈值T(本文选取T=20)，则采用双线性插值算法，反之则用双三次插值计算。

2.2 三角网格线性插值算法

经过ZNCC 算法和基于区域的插值算法处理后，视差图中产生空值(NaN)区域，即视差图中的黑色区域。三角网格线性插值算法能够根据空值区域周围的视差值估计空值区域的视差值。三角网格线性插值算法主要根据数据点来产生三角网格，然后再使用“Linear”、“Cubic”、“Nearst”等方法来进行插值，只要NaN 点附近有数据，那么就可以利用附近的数据插值计算得到NaN 点的值。

3 双目立体视觉三维重建

双目立体视觉[19]是由摄像机从不同角度同时获得被测物体的两幅图像，采用视差原理和三角测量原理，根据相机的内外参数以及图像各个特征点的对应关系恢复其三维空间坐标值（图4）。

图4 双目立体视觉成像原理Fig.4 Binocular stereo vision imaging principle

在该成像原理中，X,Y,Z为相机坐标系，通常将左相机坐标系当作世界坐标系，x-y为图像坐标系，u-v为像素坐标系。设空间点P=(X,Y,Z)在左右两个成像平面上形成的投影点分别为P´和Pʺ，其在像素坐标系下的坐标分别为P´=(u1,v1)，Pʺ=(u2,v2)；在图像坐标系下的坐标分别为P´=(x1,y1)，Pʺ=(x2,y2)；两点在平面X-Z的投影点分别为P´1和Pʺ1。左、右相机中心OL和OR之间的距离为基线B，在图像平面的投影点分别为O1和O2。图像平面与相机中心的距离为f，因此OLO1=ORO2=f。经过立体校正后，P´与Pʺ的纵坐标相同，即v1=v2，y1=y2。

根据相机投影成像模型[20]有

图中P1为空间点P 在OLXZ平面的投影，因为三角形P1P´1Pʺ1与三角形P1OLOR相似，根据相似三角形原理[21]，可得：

上式u1-u2=d，为对应点的视差值，其值即为上部分所求的视差图上每点的像素值。

点O1的像素坐标为O1=(u0,v0)，可得x1=u1-u0，y1=v1-v0。根据式(5)(6)可得空间点P的三维坐标：

根据双目立体视觉的成像原理，再结合摄像机的内外参数[22]以及视差图可以得到物体的三维坐标，恢复物体的三维结构。

4 结果与分析

分别用双线性插值和双三次插值以及基于区域的插值算法对原视差图进行处理，处理后的视差图如表1 所示，算法的运行时间如表2 所示。

表1 各种算法处理后的视差图Table 1 Disparity diagram after processing by various algorithms

表2 各个算法运行时间对比Table 2 Comparison of running time of each algorithm

对比表1 中的椭圆区域发现，双三次插值算法处理后的视差图明亮区域明显减少。根据表2，对比基于区域的插值算法与双三次插值处理后的视差图发现，基于区域的插值算法在不影响视差图质量的情况下，运算时间还少于双三次插值运行时间，这样降低了对这个视差图插值处理的计算量。

对基于区域的插值算法处理后的视差图施加三角网格线性插值算法获得视差图如图5 所示。图5 中视差图的黑色区域明显比基于区域的插值算法处理后的视差图中黑色区域减少，得到的视差图比较稠密并且比原来平滑。

表3 为视差图中NaN 值像素点所占比例，由表中数据可以得出经过本文算法处理后的NaN 值数量减少，因此得到的视差图比原来稠密且平滑。

图5 三角网格线性插值算法处理后的视差图Fig.5 Parallax diagram after processing by triangular mesh linear interpolation algorithm

表3 NaN 值所占比例Table 3 Proportion of NaN values

重建效果如图6 所示，对比图6 中的重建效果发现，经过视差图平滑处理后，三维重建模型片状点云现象减少，点云之间不再孤立，重建模型整体拼接更加自然，从而验证了本文算法的有效性。

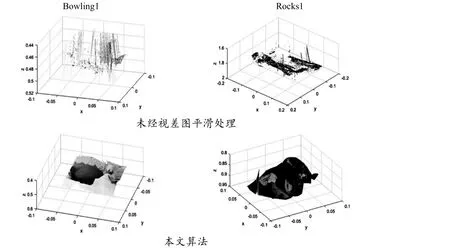
图6 三维重建效果Fig.6 3D reconstruction effect

5 结论

利用双目立体视觉进行三维重建具有广阔的应用前景。立体匹配是双目立体视觉的关键步骤，易受遮挡、视差间断等因素影响，导致在视差图中存在较多的误匹配区域，直接影响三维重建效果。为了消除误匹配区域、获得平滑的视差图，进而实现良好的三维重建，本文主要从四个方面展开了研究：(1)分析立体匹配原理和过程，以标准数据集中的Bowling1 和Rocks1 图像对为示例，立体匹配获得视差图，并指出误匹配区域；(2)为了保证视差图质量，同时提高算法的处理效率，采用基于区域的插值算法，引入阈值：在像素变化较小的平坦区域，采用双线性插值算法；在像素变化明显的区域，采用双三次插值算法；(3)经过ZNCC 匹配算法和基于区域的插值算法处理后，视差图中产生空值（NaN）区域，采用三角网格线性插值算法由空值区域周围的视差值估计空值区域，实现视差图填补；(4)利用视差图和三角测量原理进行三维重建。通过实验验证本文算法，实验结果表明本文所提算法能够很好的实现三维重建。

本文所提方法能够较好地恢复物体的三维结构，同时减少了计算量、提高了处理效率。