基于KNN 和BP 神经网络的物联网预测模型

于浩

国网安徽省电力有限公司信息通信分公司,安徽 合肥 230041

从第一台联网的ATM（自动取款机），到第一台联网的笔记本电脑，再到第一个联网的移动电话、第一台联网的汽车、第一只联网的电表……，越来越多的设备通过蜂窝网、NFC、RF-ID、蓝牙、ZigBee 和Wifi 等连接方式连到网络上。根据华为公司的预测，到2025 年将有超过1000 亿个物体（不包括个人宽带用户）被连接起来。任何物体，在任何时间和任何地点都能连接到网络上，物联网（Internet of Things,IoT）正在深刻地影响着人们的生产和生活。在物联网中，各种无线传感器将从物理世界获取到的信息（信息获取功能），通过泛在的连接和网络管道传送给各种智能的应用进行信息加工和决策（信息处理功能），智能应用将决策的结果施效到物理世界里，将关注的对象控制在预期的运动状态（信息的施效功能）。在这个过程中，泛在的连接充当了非常重要的角色，尤其是处于网络边缘的无线传感器网络，它们需要支持多样性的连接方式。但是，有源标签使用的射频技术是多种多样的，比如标签使用的射频技术可以是RFID、BLE 或Zig Bee 的。接入设备如何快速融合IoT 领域多样化的无线接入方式，是需要解决的问题，为了解决无线传感器网络数据丢失异常问题，本文利用KNN 结合BP 神经网络提出网络预测模型，增强无线传感器网络的可靠性。

1 物联网传统预测方法

1.1 指数平滑模型

指数平滑预测模型是由罗伯特.布朗首次提出的，该模型的遵循时间序列特征，事物的预测应该满足规则性和稳定性，在时间刻度上，相邻更近的结果越可能在未来预测模型的权重更大，结合模型中的每个时间序列的指数平滑数值与之前的一小段时间的指数平滑值参考加权法平均，可以采用一次指数的加权平均，也可以使用二次指数的加权平均，利用指数平滑值进行预测，其数学一次和二次指数平滑的数学模型如式子（1）和式子（2）所示。

其中st代表一次指数平滑数值，α代表权重，每个时间段的数据为yt，下一时间段要预测的数据则是yt+1，而二次指数的模型的系数权重值要根据式子（3）计算出，通过测定这些系数，计算出二次指数平滑的预测值。

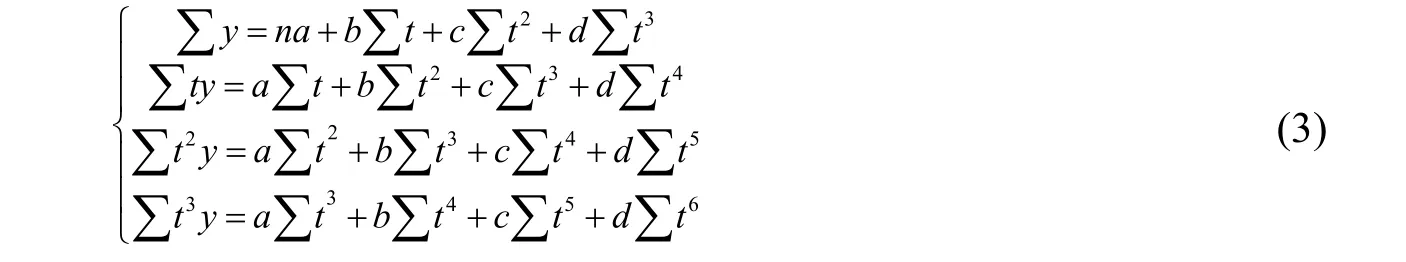
1.2 简单移动平均模型

目前该模型预测方法实现较为简单，主要是利用一段时间序列内的数值受到周期性影响后，来预算未来时间内时间发生的可能性，其数学模型的表达如式子（4）所示，通过移动平均的方法减少不明确波动的作用，其中预测值为wt+1，N代表样本的总数。

1.3 灰色预测模型

灰色预测模型是介于白盒预测与黑盒预测之间的预测方法，相比于白盒中要素全部明显和黑盒预测中的要素未知状态，灰色预测方法主要针对部分要素未知和已知的状态。在时间尺度上，事件序列有n个要素，其表示为式子（5）所示，随着时间推移，事件状态进行积累，新的序列值为式子（6）所示，该序列的微分方程如式子（7）所示。

其中的参数μ指明内生的控制灰值，α为发展灰数。利用最小二乘法求解得到预测模型的数学表达为式子（8）所示，其中X1(k+1)为预测值。

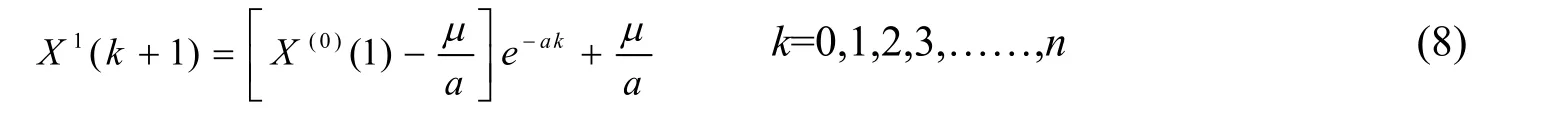
2 神经网络预测模型

2.1 BP 神经网络

BP 神经网络的模型由输出节点输出模型和隐含层节点输出模型组成，该神经网络模型具有反向误差反馈的特征，是一种具有多层传递函数的学习型网络，其网络架构如图1 所示，它具有三个层次，这三层分别是输入层、中间层以及输出层，输入层获取外界的信息，将信息传递给中间层，经过中间层的各个神经元的计算，传递给输出层，在中间层的过程中，可以由单隐藏层或多隐藏层来处理。

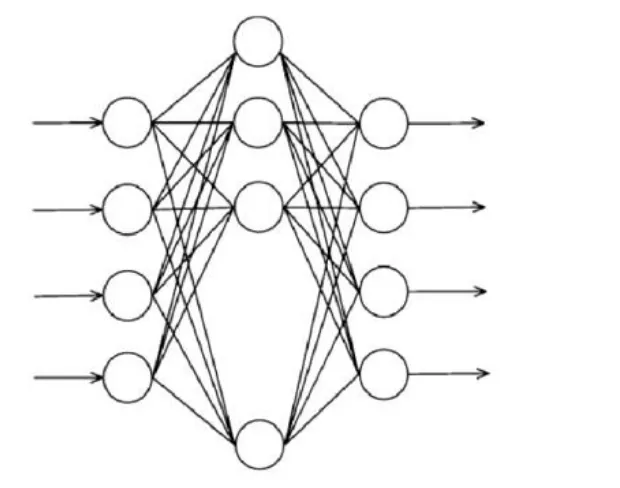
图1 BP 神经网路结构Fig.1 BP neural network structure

隐藏层节点到输出层节点的权重不同，连接权重系数分成两部分，由输入层节点Df连接到中间层节点Dm的权重系数设为wfm，而中间层节点Dm到输出层节点Dj设为wmj，指明当输出层将信息输出给外界时，会将输出值与实际值进行对比，当误差达到无法满足系统要求时，通过反向传播的方式，调整修正各层节点的权重值。在这个权重值不断修改的过程也是神经网络进行训练学习的过程，在这个学习的过程中采用最速下降法，直至达到训练模型的目的，后者满足预定设置的神经网络训练次数。实现该神经网络的算法流程如图2 所示，隐藏层的误差计算和自学习的数学模型表达式分别如式子（9）和（10）所示，在自学习的过程中网络中顺序传播方向与反向传播的过程是反复交替出现的，而在物联网的预测模型中需要将网络中的变量进行归一化的处理。

其中，tpi代表节点i的期望输出值，而Opi则是指对于节点i来说的实际输出值。式子（10）中的m作为学习因子，α代表动量因子，φ和O都代表是计算误差值。

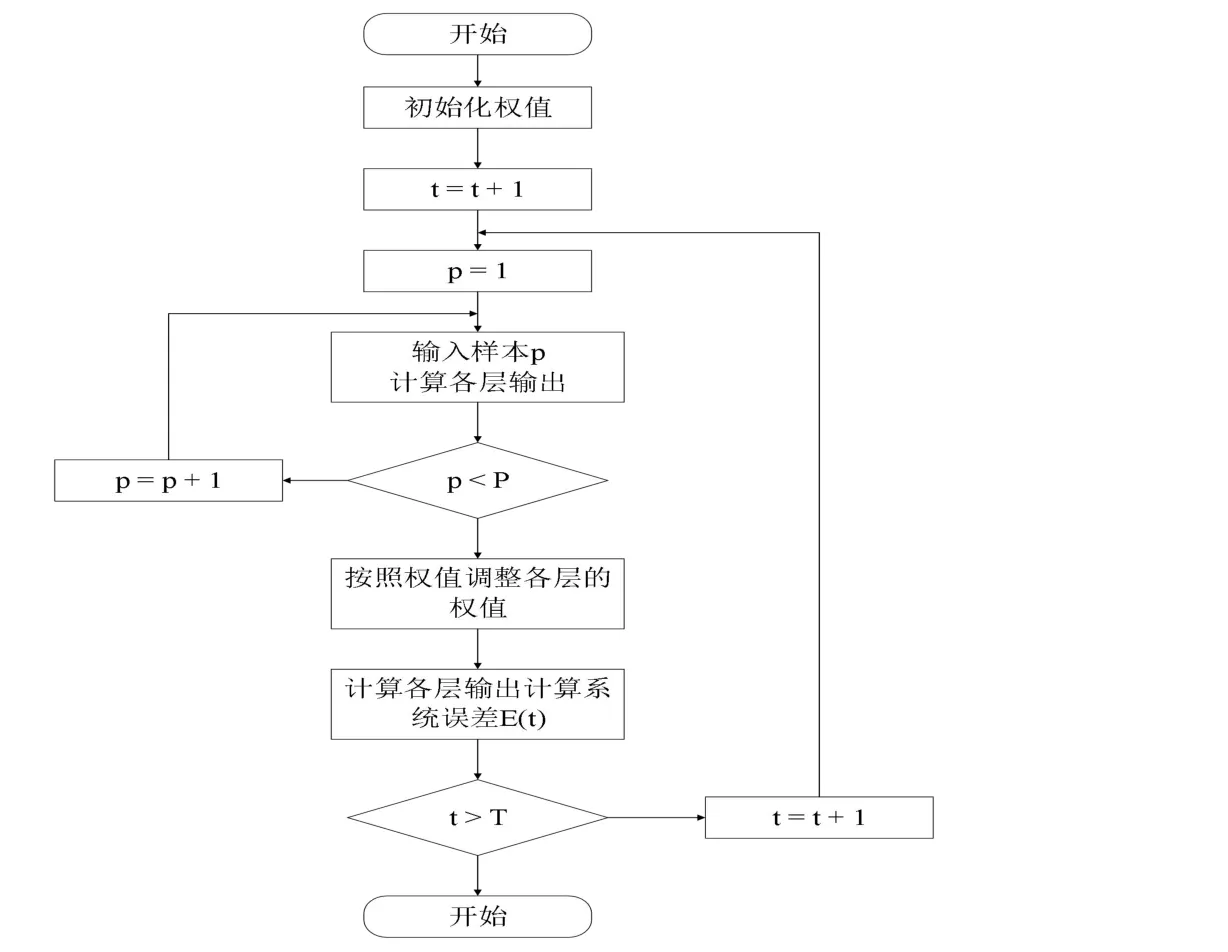
图2 BP 神经网络算法流程Fig.2 BP neural network algorithm process

2.2 KNN 算法理论

K近邻算法主要是用来计算待测样本数据与总体样本数据的距离，然后将最相邻的样本数据作为决策对象来使用该算法。KNN 算法中最为重要的部分就是三要素，分别是k值的选取、分类决策的方式以及如何度量距离。其基本思想可以理解为对于某个未知样本数据与从样本集合中k个样本是最近邻的关系，当这k个样本符合一个具体的类别时，也就确定了未知样本是也属于该类别。其中的相似度表示形式是通过欧拉距离来进行度量，其表达式如式子（11）所示。

其中，Vi=(vi1,vi2,…,vin)作为一个样本，表达式的值越小，说明欧拉距离越小，越是满足最近邻的条件，两个样本的相似度越大，当使用KNN 算法时，应进行适当地修正，改为式子（12），表明只有正常的数据值参与运算，用于预测。

对于k值的选取分析，k值对预测结果具有很大的影响，较小的k值造成分类的不准确，无法体现样本的实际意义，而较大的k值则会引入无关的样本数据，造成样本分类精度的下降。对于KNN算法的衡量可采用均方差来表示，用来描述样本的分布程度，如式子（13）所示，其中，为期望值，xi代表每个样本数据，n代表数据样本总数。

3 预测模型的分析

3.1 基于KNN 和BP 神经网络的模型流程

KNN 算法结合BP 神经网络的预测模型如图3 所示，该预测模型的预测流程是首先将输入数据输入到判断窗口，当存在异常值时，会经过KNN 算法的校正，将丢失的数据或者是异常的数据值由KNN 算法估计值来代替，然后将修正的值传递到BP 神经网络中进行学习训练，建立起基于正确输入数据的模型，BP 神经网络则是依赖于知识库中的数据不断进行训练，最后给出预测值。

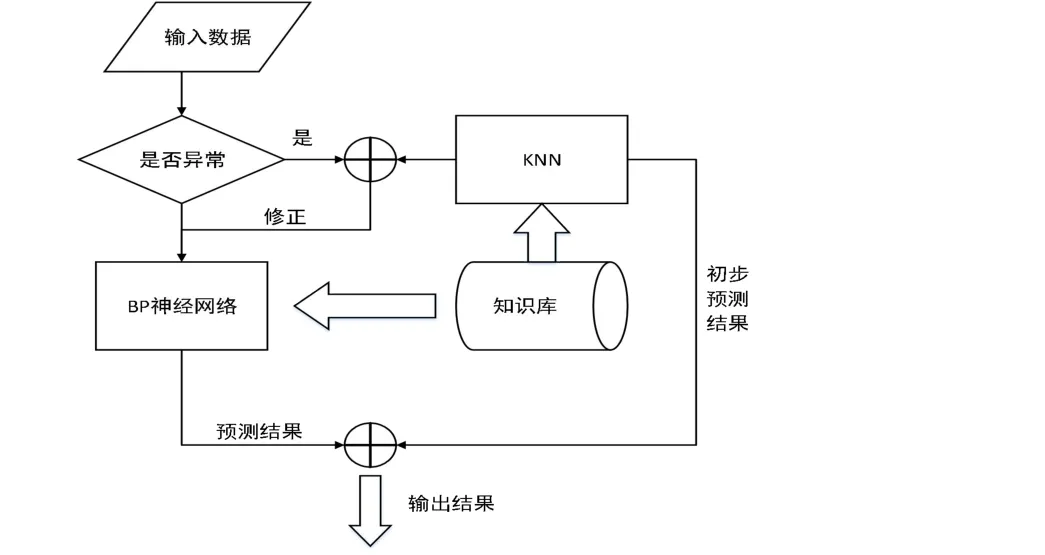
图3 结合KNN 的BP 神经网络预测流程图Fig.3 BP neural network prediction flow chart combined with KNN

对训练样本数据流程进行算法描述，首先假设输入的数据的原始样本为W，数量为n个，最后得到训练后的样本为WKNN，在数学上的处理，可以将初始样本W分成两个结合W1和W2，对于变量i满足i∈(0,N]的自然数，针对每一个Wi，考查数据是否正常，不正常将其剔除，置于W2异常数据集合，如果正常，则置于W1正常数据集合。而对于异常数据集合W1，利用KNN 的方法，在正常数据集合W1中选取k个最近邻样本数据，然后通过计算出k个最近邻的权重系数，从而得到W2KNN，处理完成后对集合合并成WA，训练结束后预测新样本，利用新的集合输入到BP 神经网络中，进行模型预测。此时对输入的新样本Y，预测结果。假设μ1为KNN 方法初步的预测概率，当样本Y满足矫正条件，从WA中选取k个最近邻，计算取代异常值权重后，组成新的集合YA，找到样本YA属于某类别的概率为P1，再利用BP 神经网络对YA预测，得到P2中概率值最大的类别。α、β分别表示KNN 与BP 神经网络进行预测的置信度权重系数，应满足α+β=1。

3.2 预测模型的实验结果

为了对模型的预测误差进行分析，选取安放在不同大楼外的位置的无线传感器，设置对比实验组，在相同的时间段内采取诸如光照、湿度、温度和气压等参数来对比，依照这些气候参数来预测未来几天无线传感器所在位置的天气状况，分析哪种模型预测得更加精准。为了简单起见，主要将预测环境的天气结果分为下雨、阴天和晴天。选取200 条数据样本作为输入，同时设定k值为5，预测算法的置信度权重设置为α=0.3、β=0.7，异常数据个数大于3 时，判断为无效样本，所以针对异常个数分别为0、1、2、3 时分析预测结果。实验的对比结果如表1 所示。

表1 训练数据集的模型预测结果Table 1 Model prediction results of training data

由上表，可以分析出当异常数目增加后，普通的BP 神经网络的预测能力开始下降，准确性有所降低，并不能适应无线传感器易于数据异常的场景，而结合KNN 的BP 神经网络的预测能力基本一致，适应能力很强，当异常数目保持在一定数值范围内，预测准确几乎不受影响，更适用于无线传感器摆放较为分散的特点，保证输入的数据样本的完整性。

4 结论与展望

本文针对于物联网场景中无线传感器数据容易出现异常的特点，首先分析BP 传统的预测模型，然后提出利用BP 神经网络结合KNN 算法来解决的方法，K近邻算法对于调整补充异常值具有良好的数据稳定性，增强了预测模型的准确性，该方法相比于传统的BP 神经网络算法具有更高效的算法实现，均方差更小，对于确保在样本数据值没有丢失和突变的情况下，保证预测数据模型具有最好的预测意义。对于没有属性经验的样本数据，计算出经验预测值往往是困难的，而采用文中的预测模型具有更明显的算法优势，使用该种方法并在实际的案例中应用该方法，具有一定的参考价值。在后续的研究中，还会继续展开优化该预测模型，例如可以引入深度学习的方式来训练模型，利用信息融合技术，进一步地提高在物联网环境中无线传感器网络的预测精度与效率。