适用复杂劣化趋势的轨道不平顺鲁棒建模方法

杨雅琴，徐 鹏*，李 晔，孙全欣

(1.北京交通大学交通运输学院，北京100044；2.中国铁路南昌局集团有限公司，南昌330002)

0 引 言

各国铁路均利用运营线路上钢轨在三维空间中的投影与其理想位置的偏差量化轨道不平顺状态，包括轨距、水平、多种弦长的高低和轨向等参数，通过峰值和轨道质量指数(Track Quality Index，TQI)评价轨道局部和整体不平顺状态[1].为保证行车安全、平稳和舒适，铁路工务部门开展轨道维修作业，将轨道状态控制在允许范围内.掌握轨道不平顺劣化规律，预测其未来发展状态，是合理安排维修作业计划，实现铁路线路预测性维修的基础，对铁路智能化运营管理具有重要意义.国内外学者围绕预测轨道不平顺劣化开展了大量研究.Andrade 等[2]通过条件自回归(CAR)建立了维修作业后高低值和劣化速率函数，据此建立了轨道高低不平顺分层贝叶斯劣化模型；曲建军等[3]将灰色GM(1,1)与基于残差修正的改进马尔可夫链相结合，建立改进灰色—马尔可夫链组合预测模型描述两次维修作业之间的轨道不平顺劣化过程.

因维修作业明显改变轨道不平顺状态，学者以单一函数或者组合函数(线性、指数等)建立两次维修作业间的轨道不平顺劣化模型.通过假设维修作业前轨道不平顺的初始状态和劣化率服从特定函数，将轨道不平顺劣化模型的时间域拓展到多次维修之间.上述假设在路基支撑刚度一致和自然气候条件变化不大的区段是成立的.但我国地域广阔，南北温差和降雨差异较大，南方和西南地区土壤中含有膨胀土，轨道劣化复杂多变；另外，维修作业(如大机捣固、换轨等)会改变轨道刚度.所以，上述假设在实际运营线路的大部分区段是很难满足的.因此，根据维修作业在时间维度上对轨道不平顺劣化过程进行分段是深入研究轨道劣化规律的前提.中国国家铁路集团公司(简称国铁集团)从2016年在全国各铁路局集团公司推广应用《铁路工务安全生产管理信息系统》，积累了近3～4年的维修作业地点和日期信息.我国铁路上，检测列车运行条件下轨道不平顺设备包括高速铁路上的综合检测列车和综合巡检车，以及普速铁路上的轨道检测车(以下统称为动轨检车)，将其检测数据统称为动态检测数据.动态检测数据是计算TQI 的数据基础，也是铁路部门感知轨道状态的重要依据.动轨检车在检测过程中，不可避免地受到环境或检测系统故障影响，产生异常检测数据，使计算得出的TQI异常，这将对轨道不平顺劣化过程中维修作业的判别造成干扰.

综上，本文基于最小描述长度准则探索建立一套动态检测数据驱动的轨道不平顺劣化自适应分段建模方法(Minimum-Description-Length-Based Rail Track Deterioration Adaptive Segmentation Framework，MDL-RTDAS). MDLRTDAS 能够克服检测数据异常影响，灵敏感知劣化趋势的变化，自动识别轨道不平顺劣化过程中维修作业发生的日期.本文将为正在开展的“通过挖掘高铁历史检测数据，掌握高铁开通十年来劣化规律，指导高铁预测性维修”奠定可靠的数据挖掘基础.

1 轨道不平顺劣化自适应分段建模方法

1.1 最小描述长度准则

将轨道劣化过程中维修作业发生的日期称为维修作业点.轨道不平顺劣化趋势会在维修作业点处发生突变.因此，维修作业点的识别问题类似于应用统计学中时间序列突变点的识别.基于最小描述长度(Minimum Description Length，MDL)准则的突变点识别方法是一种不需要突变点个数和位置等先验知识，依据时间序列特征进行识别的方法.Davis[4]基于MDL准则和AR模型，建立了一套自动识别非平稳时间序列突变点的模型.LU Q.Q.等[5]利用MDL准则估计具有自相关性和周期性的天气时间序列中的突变点.MDL 准则是Jorma Rissanen 提出的最优编码理论[6]，基本原理是采用某种模型对数据进行编码，用编码后的数据和模型表示原始数据，编码后占用存储空间(称为总描述长度)最小的编码模型，即为最优编码模型.基于MDL准则识别时间序列突变点的核心思想是将识别问题转化为模型选择问题，即通过搜索能够最完整保留原始数据包含信息同时最大程度将其压缩的最优拟合模型，估计突变点的个数和位置.

依据MDL 准则，总描述长度分为两部分：模型的编码长度和对应残差的编码长度.对于长度为l的时间序列y={y1,y2,…,yl} ，其中，y1,…,yl为时间序列y中的元素；选择模型拟合y，令表示y的拟合值，则对应残差为以Ly表示y的编码长度，则Ly可分解为

1.2 MDL-RTDAS

MDL-RTDAS 通过识别轨道劣化过程中维修作业导致的劣化状态突变，自动将劣化过程分段，使用线性回归模型拟合每一段劣化过程，据此，建立轨道不平顺劣化自适应分段模型.这种方法不依赖维修作业记录，不假设检测数据有效性，完全由动态检测数据驱动，能够适应各种自然条件下的轨道劣化建模.

根据式(1)推导线性回归模型的编码长度和残差编码长度的具体过程如下.

(1)模型编码长度.

轨道高低不平顺VTQI-L是安排维修作业的主要状态指标，故本文主要围绕轨道高低劣化进行研究.采用一元线性回归模型拟合每一段子变化过程，设某一时间段内进行了n次动态检测，每次检测日期为t1,t2,…,tn，记其集合为t={t1,t2,…,tn} ，某200 m 线路单元在各次检测的VTQI-L值为q1,q2,…,qn，记其集合为q={q1,q2,…,qn} ，期间进行过m次维修作业(0＜m ＜n)，第j个和第j+1个子过程之间的维修作业日期为τj，令τ0=t1，τm+1=tn，则第j个子过程的拟合模型表示为

式中：βj={βj0,βj1} 为第j个子过程拟合模型的参数集合，其中，βj0为截距，βj1为斜率；ε为随机项，令μe为ε的均值，为ε的方差，则可见，的待估计参数包括τj和βj.令表示所有子过程拟合模型的集合，则表示为

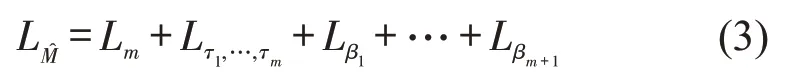
令nj=τj-τj-1代表第j个子过程包含的数据点数，则(τ1,…,τm)与(n1,…,nm+1)蕴含的信息是等价的，式(3)可转换为

依据MDL准则：对于有限整数I，若I的上限未知，则LI=lbI；若I的上限已知，设为IU，则LI≈lbIU.通过极大似然估计拟合N个观测值，得到的一元线性回归模型参数的编码长度为由此，可得

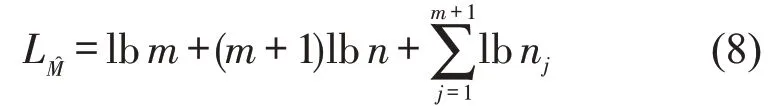
(2)模型残差编码长度.

对于Le，MDL 准则中给出定义：拟合模型的残差e的编码长度Le为的负对数似然估计(以2为底)[6].令表示q的估计值，则中各子过程拟合模型相互独立，可得

将式(8)和式(9)相加，得到轨道不平顺劣化分段拟合模型的编码长度，记为Lq.为简化运算，将对数底由2换为e，得到

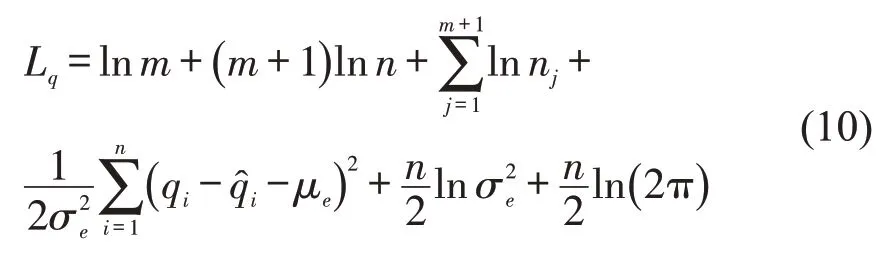
式(10)为本文解决轨道不平顺劣化过程中维修作业点识别问题的目标方程式，使式(10)取得最小值的一组模型，即为轨道不平顺劣化的最优分段拟合模型，其对应的分段点则为要识别的维修作业点.

2 模型求解

在突变点个数未知的情况下，求解式(10)最小值的计算量很大.本文数据VTQI-L具有以下两个特征：①样本量小，根据《普速铁路线路修理规则》对动态检测周期的规定及现场调研，主要繁忙干线1个月有2次检测[1]，故研究对象的样本量较小；②检测异常值干扰较大，异常检测数据的存在对识别维修作业点造成干扰，如何克服检测数据异常的干扰是本文设计模型求解算法要考虑的关键问题之一.结合研究数据特征，克服异常检测值的干扰，同时减小计算复杂度，模型求解算法具体步骤如下：

Step 1确定疑似维修作业点.

轨道高低不平顺劣化过程中异常点和维修作业点的特征明显：异常点明显偏离当前的劣化趋势，进行一次维修作业后，高低不平顺值会降低到规定范围内，进入下一个劣化过程.如图1所示.

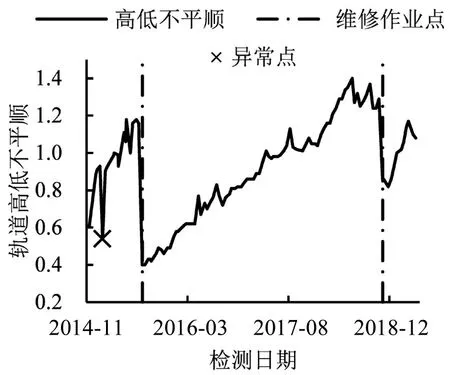
图1 轨道高低不平顺劣化过程中的异常检测数据及维修作业Fig.1 Maintenance operations and anomalous measurements in track longitudinal level irregularity deterioration

将异常点和维修作业点统称为疑似维修作业点，令di=qi-qi-1表示VTQI-L的一阶差分，记其集合为d，则疑似维修作业点的一阶差分会明显偏高/偏低.设ωi为衡量某点一阶差分值与相邻点的差异程度，则有

设一阶差分d的上四分位数为W0，当ωi ＞W0时，认为该点对应的检测日期ti为疑似维修作业点.

Step 2计算不同分段方式的MDL值.

确定疑似维修作业点后，设其个数为.假设从个疑似维修作业点中选取r个，利用动态规划方法求得令MDL值最小的r个疑似维修作业点的组合方式，记其最小值为Mr|min.考虑到1 个月内同一个线路单元不会安排两次维修作业[1]，故在组合疑似维修作业点时，若存在相邻两点的时间差小于1个月，则认为该种组合方式无效.

Step 3选择最优分段方式.

根据MDL 准则，令MDL 最小的为最优拟合模型.但实际分析时发现，对于本文研究对象，当MDL 值最小时，往往将轨道不平顺劣化过程过度分段，不利于劣化过程分析.分析Mr|min随被选疑似维修作业点的个数r增加的变化过程，认为当|Mr+1|min-Mr|min|小于阈值δ时，Mr|min对应的疑似维修作业点组合方式为最优.最优分段拟合模型的分段点，即为本文要识别的维修作业点，未被选中的疑似维修作业点认为是异常点.在本文中，δ=10.

3 计算验证

数据来源于2014—2019年昌福高速铁路下行K21+184～K220+308的原始动态检测数据.原始动态检测数据的里程偏差修正和波形对齐，各项TQI计算等一系列数据预处理过程依托团队研发的《基于动态检测数据的轨道变形分析系统》完成[7].MDL-RTDAS 的关键是劣化过程中维修作业点的识别，选取多个200 m 线路单元区段，针对这些区段劣化过程中的维修作业点，对比分析MDLRTDAS 的识别结果和人工分析确认的结果，同时展示Davis等的Auto-PARM[4]在这些区段上的识别结果，据此来验证MDL-RTDAS的有效性.

3.1 案例分析

选取3 个区段，直观对比MDL-RTDAS 与Auto-PARM 的识别结果及分段拟合模型，分别计算两个模型拟合残差的均值(EMR)、标准差(ER-SD)和平均绝对值(EMAR)，对比分析拟合效果.图2(a)、图3(a)和图4(a)为本文MDL-RTDAS 的识别结果及分段拟合模型，图2(b)、图3(b)和图4(b)为Auto-PARM 的结果.图中，实线代表该区段的实际高低不平顺值，虚线代表模型计算出的拟合值，垂直线代表模型识别出的维修作业点.

(1)区段1(K84+601～K84+801).

该区段位于曲线上，根据其轨道高低不平顺劣化过程分析出该区段于2015-07-24、2017-12-26进行了维修作业.MDL-RTDAS识别出的维修作业点为2015-07-24、2017-12-26，如图2(a)所示；Auto-PARM 识别出的维修作业点为2015-07-24、2016-01-12、2016-08-12、2017-01-11、2017-12-26、2019-03-21，如图2(b)所示.通过两个模型拟合的残差计算得到的EMR、ER-SD、EMAR如表1 所示，可得MDL-RTDAS拟合残差的均值更接近于0，离散程度更小，平均绝对值更低.

图2 K84+601～K84+801 (位于曲线上)Fig.2 K84+601～K84+801(on a curved track)

表1 两个模型的残差对比分析(区段1)Table 1 Residual comparison analysis of section one

(2)区段2(K103+334～K103+534).

该区段位于直线上，根据其轨道高低不平顺劣化过程分析出该区段于2016-06-26、2016-11-26、2018-09-11 进行了维修作业.MDL-RTDAS 和Auto-PARM 识别出的维修作业点均为2016-06-26、2016-11-26、2018-09-11，如图3(a)、(b)所示.通过残差计算得到的EMR、ER-SD、EMAR如表2 所示，可得MDL-RTDAS拟合残差的均值更接近于0，离散程度更小，平均绝对值更低.

图3 K103+334～K103+534 (位于直线上)Fig.3 K103+334～K103+534(on a tangent track)

表2 两个模型的残差对比分析(区段2)Table 2 Residual comparison analysis of section two

(3)区段3(K106+551～K106+751).

该区段位于直线上，根据其轨道高低不平顺劣化过程分析出该区段于2016-07-14、2017-09-12、2018-01-26 进行了维修作业.MDL-RTDAS 识别出的维修作业点为2016-07-14、2017-09-12、2018-01-26，如图4(a)所示；Auto-PARM 识别出的维修作业点为2015-04-13、2016-07-14、2018-01-26，如图4(b)所示.通过残差计算得到的EMR、ER-SD、EMAR如表3所示，可得MDL-RTDAS拟合残差的均值更接近于0，离散程度更小，平均绝对值更低.

图4 K106+551～K106+751 (位于直线上)Fig.4 K106+551～K106+751(on a tangent track)

表3 两个模型的残差对比分析(区段3)Table 3 Residual comparison analysis of section three

3.2 综合对比

为进一步对比分析，另选若干区段统计分析每个区段劣化过程中异常检测的个数MF,两个模型拟合的残差，以及识别结果的准确率(PARC)、精确率(PPRC)，结果如表4所示.

式中：NT为模型正确识别出的维修作业点个数；NF为模型中错误识别的维修作业点个数；Mmanual为人工分析出的维修作业点个数.

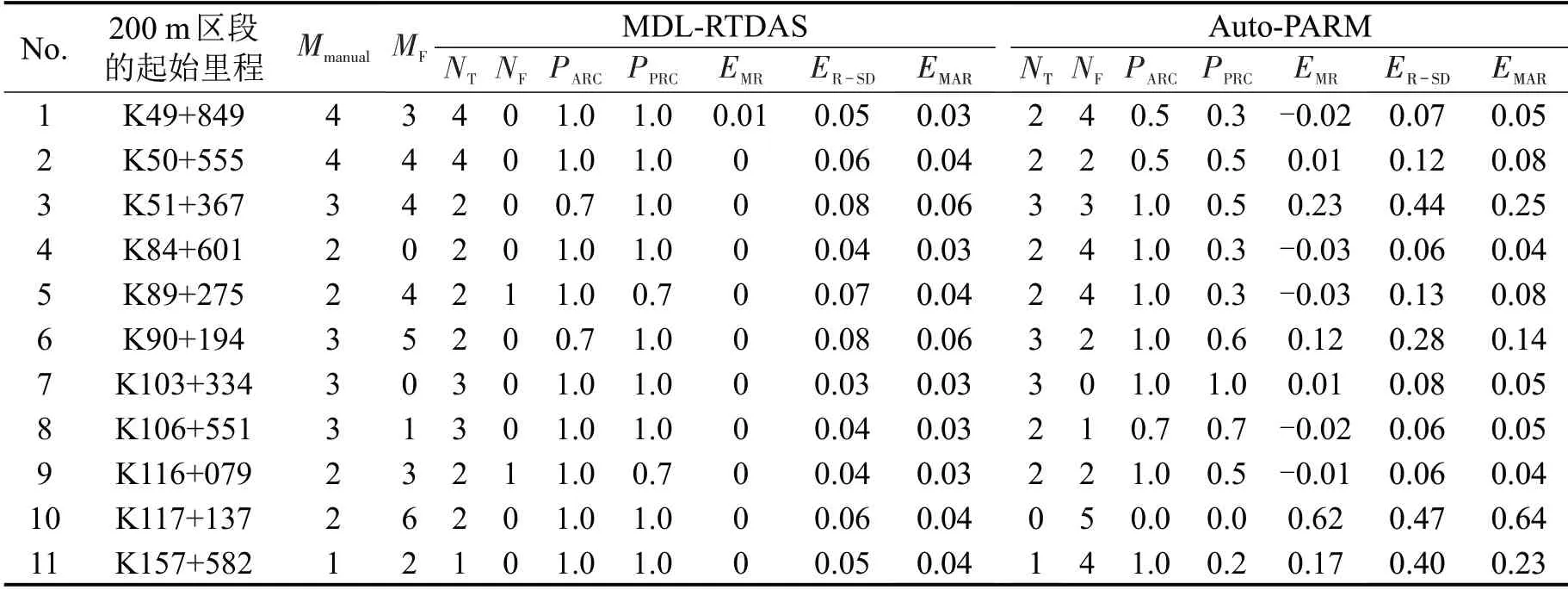
表4 两个模型的识别准确度及拟合效果Table 4 Accuracy,precision and fitness of two algorithms

基于两个模型识别的准确率和精确率，令Fscore表示衡量模型的识别准确度，则Fscore=0.5×PARC+0.5×PPRC.根据表4计算得到：两个模型在各区段的Fscore，对比结果如图5(a)所示；两个模型拟合残差计算的EMAR，对比结果如图5(b)所示；MF对PARC的影响，如图6所示.

从表4 中EMR和ER-SD可得，MDL-RTDAS 建立的分段拟合模型残差的均值更接近于0 且离散程度更小；从图5(a)可得，MDL-RTDAS 的识别准确度高于Auto-PARM；从图5(b)可得，MDLRTDAS 拟合残差的平均绝对值低于Auto-PARM；从图6 可得，随着区段中异常检测数据的增加，MDL-RTDAS 的识别准确率没有随之变大/变小，说明MDL-RTDAS 可克服检测数据异常的影响.综上，MDL-RTDAS更适用于轨道高低不平顺劣化自适应分段建模，且具有一定的鲁棒性.

图5 两个模型识别准确度及平均绝对拟合误差对比情况Fig.5 Comparison between two algorithms'performances

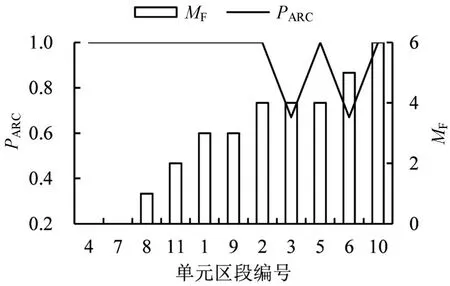
图6 异常检测数据对MDL-RTDAS 识别准确率的影响Fig.6 Effect of contaminated measurements on PARC

4 结 论

本文提出将维修作业导致轨道不平顺劣化过程突变的识别问题转化为模型选择问题，并基于最小描述长度提出动态检测数据驱动的轨道不平顺劣化自适应分段建模方法MDL-RTDAS.在难以确保维修作业记录完整，检测数据全都有效的情况下，MDL-RTDAS 能够克服检测数据异常的影响，灵敏感知到轨道劣化过程中劣化趋势的变化和自动识别轨道不平顺复杂劣化过程中的维修作业，实现轨道不平顺劣化自适应分段建模.将MDL-RTDAS应用到2014—2019年昌福高速铁路下行K21+184～K220+308的轨道劣化分析中，对其有效性进行验证.与同类算法对比，MDL-RTDAS更加有效.为进一步提高MDL-RTDAS 的有效性和精度，需要优化求解算法.考虑应用MDLRTDAS建立的轨道不平顺劣化分段拟合模型来探索轨道劣化规律，辅助工务部门制定养护维修计划是下一步的研究重点.