磁电弹结构多场耦合分析的稳定Node-based 光滑径向基点插值法

任书慧，孟广伟，王吉贤，周立明

（吉林大学机械与航空航天工程学院，吉林长春 130025）

磁电弹材料是一种由压电相（BaTiO3）与压磁相（CoFe2O4）复合而成的智能材料，能够将机械能、电能与磁能相互转化[1-2].磁电弹材料因其具有力电、力磁、磁电效应而被广泛应用于智能结构中，引起了国内外学者的广泛关注[3-4].Jiang 等[5]推导了在均布载荷作用下磁电弹悬臂梁响应的解析解，为未来磁电弹结构的设计与分析奠定了基础.Wang 等[6]求解了三维磁电弹圆柱板的自由振动问题，得出了频率方程.Ebrahimi 等[7-8]利用Hamilton 原理推导了磁电弹纳米板的非局部控制方程，研究了纳米板的屈曲行为.

由于传统有限元法（FEM）在求解中存在“过刚”、体积自锁等问题，导致结果不准确.近年来，Liu等[9]提出了广义梯度光滑技术，并基于该方法构造出了一系列光滑有限元法（S-FEM）[10]和光滑径向基点插值法（S-RPIM）[11].何智成等[12-13]和陈泽聪等[14]将光滑有限元应用到声学模拟中.周立明等[15-16]将光滑有限元扩展到了求解裂纹问题和多场耦合问题中，验证了光滑方法的准确性.在S-RPIM 中，Node-based光滑径向基点插值法（NS-RPIM）能够消除FEM 中“过刚”的问题，为所求解问题提供能量范数的上界解[9].该方法使用径向基函数对场函数进行近似，其形函数具有Kronecker Delta 函数属性，边界条件可以如FEM 一样直接施加.基于伽辽金弱形式与节点积分技术，推导出系统方程.基于这些优点，NS-RPIM在求解静力学以及多场耦合问题中得到了广泛的应用.Li 等[17]采用NS-RPIM 分析了二维、三维固体力学问题，验证了此算法的准确性与优越性.Zhou 等[18]将NS-RPIM 引入多场耦合问题的研究中，结果表明，NS-RPIM 对于求解磁电弹结构的响应问题是有效且可靠的.

尽管NS-RPIM 在求解许多问题时表现良好，但研究表明[11，19]，由于NS-RPIM 的模型过于柔软，会令其在求解动态问题时产生伪非零能量模式，导致算法存在时间不稳定性.为增强系统刚度，解决时间不稳定性，Wang 等[20]提出了一种稳定算法，解决了Node-based 光滑有限元方法中的缺陷并且减少了求解声学问题中的色散误差.Feng 等[21]提出了一种稳定的节点积分方法，分析了电磁问题.Yang 等[22]解决了Node-based 光滑有限元方法中的时间不稳定性，更准确的求解了金属成型问题.

本文提出了稳定NS-RPIM（SNS-RPIM），基于传统NS-RPIM 方法，引入与场变量梯度方差相关的稳定项，消除了不确定参数，推导了求解多场耦合问题的SNS-RPIM 方程，分析了磁电弹结构在静力作用下的响应，并将所得结果与有限元法计算结果进行了对比.

1 基本方程

磁电弹材料平衡方程如下：

式中：σij、Dl、Bl分别为应力分量、电位移分量、磁感应强度分量.

磁电弹材料的几何方程如下：

式中：Sij为应变分量；Ek为电场强度分量；Hk为磁场强度分量；Φ 与Ψ 为电势与磁势.

磁电弹材料的本构方程如下：

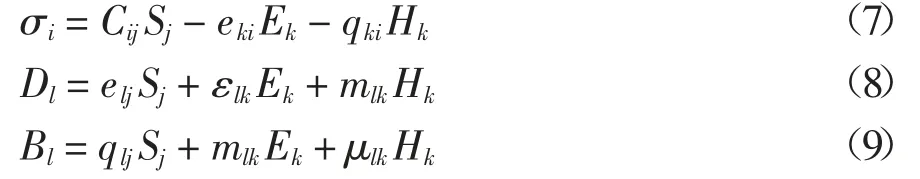
式中：Cij、eki、qki分别为弹性常数、压电系数与压磁系数；εlk、mlk、μlk分别为介电常数、磁电耦合系数与磁导率.i，j=1，2，…，6；l=1，2，3；k=1，2，3.

边界条件为：

式中：Γd与Γs分别为位移边界与力边界；Γe与Γt分别为电势边界与电位移边界；Γm与Γi分别为磁势边界与磁通量边界为Γd上给定的位移为Γe上给定的面力为Γe上给定的电势为Γt上给定的电位移；为Γm上给定的磁势为Γi上给定的磁通量.

2 稳定Node-based 光滑径向基点插值法

2.1 Cell-based T2L 方案

Cell-based T2L 方案[9]为计算xQ的形函数值选择合适的局部支持节点.该方案选择xQ周围的两层节点作为局部支持节点.第一层节点为xQ所在三角形单元的顶点；第二层节点为与第一层节点直接连接的那些节点，如图1 所示.

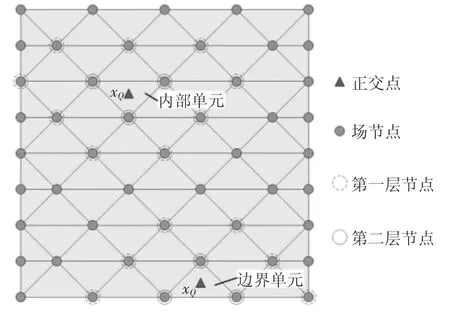
图1 Cell-based T2L 方案Fig.1 Cell-based T2L scheme

2.2 Node-based 光滑径向基点插值法

二维问题域Ω 被离散为ne个三角形单元，包含nn个节点.通过将节点xi=[xi，zi]T周围三角形的边中点与质心依次相连，构造以xi为中心的光滑域Ωi，如图2 所示.

问题域内任一点xi处的近似位移、近似电势与近似磁势可表示为：

式中：Nu（xi）、NΦ（xi）与NΨ（xi）分别为NS-RPIM 的位移形函数、电势形函数与磁势形函数；ns为局部支持节点的数量；u、Φ 和Ψ 分别表示位移向量、电势向量和磁势向量.

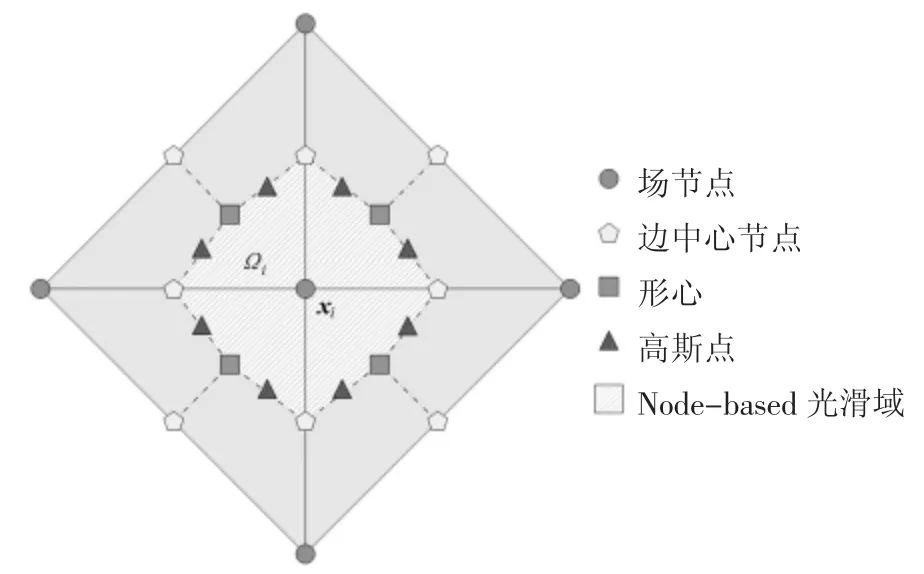
图2 基于节点xi 的光滑域Fig.2 Smoothing domain of node xi

通过引入梯度光滑技术，根据式（16）～（18），节点xi处的光滑应变、光滑电场强度与光滑磁场强度分别为：

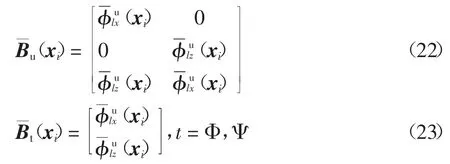
通过引入标准高斯积分，式（22）（23）中的各项可表示为：

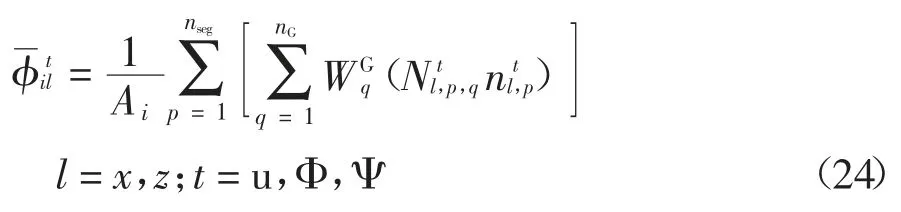
式中：nG为高斯点的数量；nseg为光滑域边界的数量；为光滑域第p 段边界中单位法向量矩阵的分量；为第p 段边界上第q 个高斯点处的形函数值；为第q 个高斯点处的权值；Ai为光滑域的面积.

二维磁电弹的NS-RPIM 静力学方程可表示为：

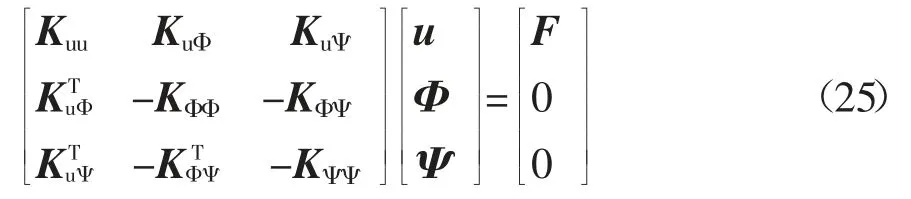
式中：F 为外力.各刚度矩阵为：

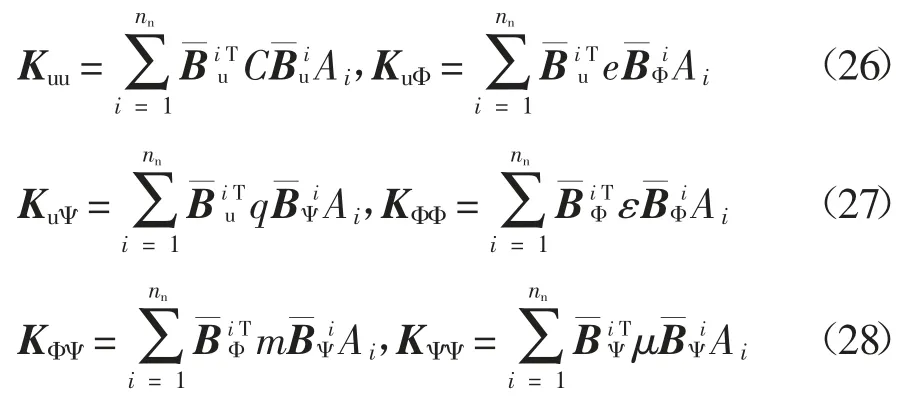
采用自由度凝聚技术[18]，式（25）可表示为：

式中：等效力向量Feq、等效刚度矩阵Keq以及电势Φ和磁势Ψ 的求解公式见参考文献[18].

2.3 稳定Node-based 光滑径向基点插值法

为了在提高NS-RPIM 计算精度的同时消除时间不稳定性，在该算法中引入与场变量梯度方差相关的稳定项来提高模型的刚度，令其更接近真实情况.

以二维问题为例，如图3 所示，光滑域Ωi被近似为具有相同面积的圆，将近似域进一步划分为4个子光滑域.局部坐标系与光滑域的交点1，2，3，4；i=1，2，3，…，nn）作为补充积分点，nn为结构包含节点数.积分点与节点xi之间的距离lc相等，大小为近似域的半径.lc的计算公式为：

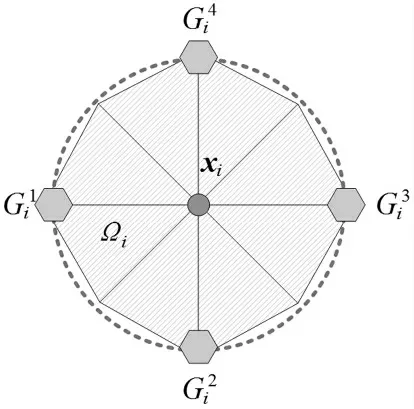
图3 SNS-RPIM 积分区域Fig.3 Integral domain of SNS-RPIM

假设场变量的梯度在光滑域Ωi中连续且一阶可导，其在4 个积分点处的泰勒展开式分别为：

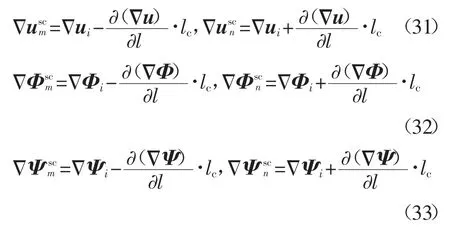
式中：m=1，2；n=3，4；l=x，z；上标sc 表示在近似域中的4 个补充积分点处进行计算.将式（31）～式（33）代入光滑伽辽金弱形式，式（25）中各刚度矩阵可以改写为：

3 数值算例

3.1 算例1

磁电弹材料（BaTiO3-CoFe2O4）板在边AD 受100 N/m2的均布载荷作用，为平面应变问题，如图4 所示，边长a=2.0 m.表1 给出了磁电弹板的材料参数，质量密度为5 730 kg/m3，边界条件为：ux=0（边CD），uz=Ф=Ψ=0（边BC），每个边界的表面电荷与表面磁感应强度均为零.

采用不同节点数量（121、441 和1 681 个）求解磁电弹板的广义位移（位移ux、uz，电势Φ，磁势Ψ），验证SNS-RPIM 的正确性以及收敛性.表2 给出了文献[23]中A 点处位移、电势与磁势的解析解，以及SNS-RPIM 在不同节点数量下的计算结果.可见，SNS-RPIM 的结果与解析解误差很小，随着节点数量的增加，误差减小，验证了SNS-RPIM 求解磁电弹结构多场耦合问题的正确性、有效性.

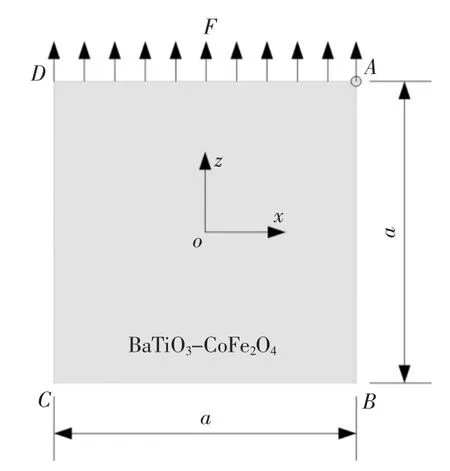
图4 磁电弹板Fig.4 Magneto-electro-elastic plate

3.2 算例2

磁电弹材料悬臂梁如图5 所示，长度L=0.030 m，宽度h=0.002 m，在B 点承受200 N 的静力，为平面应力问题.悬臂梁在固定端处满足ux=uz=Φ=Ψ=0.悬臂梁材料属性见表1，质量密度为5 730 kg/m3.

图5 磁电弹悬臂梁Fig.5 Magneto-electro-elastic cantilever beam

在证明了SNS-RPIM 正确性的基础上，对磁电弹悬臂梁在静力作用下的响应进行研究.图6 给出了边AB 处的广义位移，SNS-RPIM 与FEM 采用三角形单元，节点数量为305 个.其中，参考解为FEM采用180×12 个四边形单元的结果.图7 给出了静力作用下悬臂梁的云图.由结果可知，在所用节点数量相同的情况下，SNS-RPIM 的计算结果比FEM 的结果更加接近参考解.算例结果验证了SNS-RPIM 的高精度、正确性和有效性.

在节点数为305、637 和1 089 个时，对比了SNS-RPIM 与FEM 的能量误差[24]，如图8 所示.可知在节点数相同的情况下，SNS-RPIM 的能量误差远远低于FEM，并且随着所用节点数的增加，能量误差逐渐降低.从而进一步验证了SNS-RPIM 的精确性，高收敛性与有效性.

图6 悬臂梁AB 边界处ux、uz，Φ 和Ψ 变化趋势Fig.6 Variation of ux、uz，Φ and Ψ at edge AB of cantilever beam

图7 悬臂梁μx、μz、Φ 和Ψ 云图Fig.7 Contour of μx、μz、Φ and Ψ of cantilever beam

图8 稳定Node-based 光滑径向基点插值法与有限元法在不同节点数下的能量误差Fig.8 Energy error of SNS-RPIM and FEM with different number of nodes

3.3 算例3

磁电弹材料传感器为对称结构，在A 点受100 N 的静力F，传感器几何形状及尺寸如图9 所示，为平面应力问题.传感器边界条件为：ux=uz=0 （左右固定端处），Ф=Ψ=0（下边界处）.结构所用材料见表1，质量密度为5 730 kg/m3.

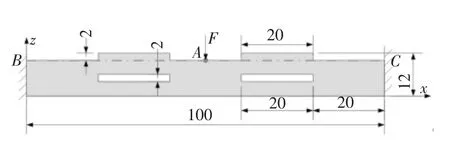
图9 磁电弹传感器（单位：mm）Fig.9 Magneto-electro-elastic sensor（unit：mm）

图10 给出了边BC 处的广义位移，SNS-RPIM与FEM 采用三角形单元，节点数量为1 157 个.其中，参考解为FEM 采用4 000 个四边形单元的结果.图11 所示为磁电弹传感器位移、电势和磁势的云图.由图可得：在同样节点条件下，SNS-RPIM 的计算结果比FEM 的计算结果更加接近参考解，从而验证了SNS-RPIM 可解决有限元系统刚度过硬的问题，提高结果的精度，能够有效求解复杂磁电弹结构在静力作用下的响应.

图10 传感器BC 边界处ux、uz、Φ 和Ψ 变化趋势Fig.10 Variation of ux、uz、Φ and Ψ at edge BC of magneto-electro-elastic sensor

图11 传感器μx、μz、Φ 和Ψ 云图Fig.11 Contour of μx、μz、Φ and Ψ of magneto-electro-elastic sensor

4 结论

本文基于场变量梯度方差构造了稳定项，并将其引入了传统Node-based 光滑径向基点插值法，提出了稳定Node-based 光滑径向基点插值法.随后求解了磁电弹结构在静力作用下的响应，得出以下结论：

1）将SNS-RPIM 的结果与解析解进行对比，二者吻合良好，说明了本方法的正确性及有效性.

2）计算了SNS-RPIM 与FEM 在不同节点数量下的能量误差，结果显示SNS-RPIM 具有良好的收敛性与准确性.

3）SNS-RPIM 利用较少的节点能够达到更高的精度，消除了FEM 模型刚度过硬的问题.

4）通过考虑SNS-RPIM 与FEM 对不同模型的求解结果，表明SNS-RPIM 在求解磁电弹结构多场耦合问题时的可靠性和适用性.