新型三瓣式径向气体箔片动压轴承热特性分析
2020-10-31冯凯李映宏张凯刘永红郭志阳
冯凯,李映宏,张凯†,刘永红,郭志阳
(1.湖南大学汽车车身先进设计制造国家重点实验室,湖南长沙 410082;2.湖南大学艺术设计学院,湖南长沙 410082;3.长江大学石油工程学院,湖北武汉 430100)
与传统油轴承和滚子轴承相比,气体轴承具有高速、高温、高功率密度、无油、免维护等诸多优点[1-2].自1969 年首个气体轴承被设计并成功应用到高速旋转设备以来,国内外学者设计开发了形式多样的气体轴承,其中气体箔片动压轴承由于其出色的承载能力和较高的稳定性能受到了学术界与工业界的极大关注.目前,气体箔片动压轴承已被成功应用于空气循环机、微型燃气轮机、涡轮增压器等超高速涡轮机械中[3-4].然而,气体箔片动压轴承作为一种滑动轴承在高速情况下容易出现转子次同步振动现象并引发设备故障.
为有效抑制气体箔片动压轴承在超高转速下的次同步振动,提高气体箔片动压轴承转子系统的稳定性,国内外学者对气体箔片动压轴承的结构进行了多种形式的改进.主要的改进形式有三种:第一种是通过在气体箔片轴承的支撑结构中增加阻尼层,如金属丝网等[5-6],利用支撑结构中阻尼材料存在的丰富摩擦学行为有效地耗散振动能量,进而提高轴承系统稳定性.但该种改进结构通常面临严重的轴承散热问题;第二种改进形式是通过引入主动控制单元[7-8],对轴承在运行过程的气膜形状进行改变,提高轴承-转子系统稳定性.该改进形式前景广阔,但存在成本高、控制系统复杂等不足;第三种改进形式是通过优化气体箔片动压轴承的截面线形[9-10],使得气体箔片动压轴承能够更加有效地形成气膜并优化气膜形状,抑制轴承-转子系统的高速次同步振动.新型三瓣式径向气体箔片动压轴承作为第三类改进形式中的典型代表,展现了优异的性能.Heshmat 等人[9]成功实现将三瓣式气体箔片动压轴承应用于120 kr/mim 超高速条件下,且实验过程中未出现任何失稳现象.针对三瓣式气体箔片动压轴承,张涛[11]搭建实验台用于测量该类轴承的动力学特性.实验结果表明,三瓣式气体箔片轴承能够对转子的振荡失稳表现出良好的抑制效果;Kim[10]研究对比了整周与三瓣形式气体箔片动压轴承的静动态特性.计算结果表明,与整周式气体箔片轴承相比,三瓣式气体箔片轴承的承载力较低,但具有更高的失稳转速.
然而,在高速及超高速情况下,气体黏性剪切会产生大量热量,同时周边的高温应用环境也会向轴承传递热量.轴承温度的升高带来了材料退化、转子膨胀干摩擦和密封泄漏等问题,这增加了新型三瓣式径向气体箔片动压轴承在高速、高温涡轮机械中的应用难度,有必要对新型三瓣式径向气体箔片动压轴承的热特性进行详细系统的分析.
对于气体箔片轴承的热特性研究起步较早,成果丰富.最初,Salehi 等人[12-13]忽略压力梯度对轴承温度的影响,对能量方程进行近似求解,虽然耦合了非等温Reynolds 方程和能量方程,但该模型仅获得沿圆周方向的一维温度分布;Peng 和Khonsari[14]建立了传统的热特性分析模型来预测气体箔片轴承的稳态性能.通过同时求解非等温Reynolds 方程和能量方程,以预测气膜压力场和温度场,但在该模型中忽略了气膜到转子与轴承套的热量传递,导致气膜温度偏高.预测结果显示,气体黏度随气膜温度的升高而发生变化,轴承的负载能力增加;Feng 和Kaneko[15-16]利用自己提出的箔片刚度模型,对箔片轴承的热特性进行了深入的研究,但建立的传热模型较为简单,只考虑到由冷却气流和泄露气体带走的热量,使得预测结果在高转速条件下与实验结果存在一定的差异;Sim 和Kim[17]提出了一种三维热特性模型,用于计算气膜、转子以及箔片的温度分布,并考虑到轴向方向上转子和壳体的热量传递,计算结果表明轴承的径向间隙对轴承的热特性影响显著.此外,Lee和Kim[18]拓展了Sim 和Kim[17]提出的模型,特别是箔片结构和冷却气流中的传热路径,并沿轴向方向通过仪器测出顶箔与轴承套之间的有效热阻;Zhang等人[19]对波箔和金属丝网混合型气体箔片轴承进行了详细的热特性分析,并考虑热量传递、热膨胀和离心增长等因素,研究转速、载荷和冷却气流对轴承热特性的影响,且实验结果与预测结果具有很好的一致性.
本文针对新型三瓣式径向气体箔片动压轴承,考虑轴承-转子系统的流体动压润滑和热效应的影响,建立非等温Reynolds 方程、粘温方程、能量方程和轴承传热模型,利用有限元方法对轴承的热特性进行研究与分析.以箔片轴承气膜区域的入口温度、转子外表面温度和顶箔内表面温度作为边界条件,对轴承气膜温度进行迭代计算.此外,本文考虑到润滑气体的可压缩性和粘温特性,也分析了转子的离心增长和热膨胀对气膜间隙的影响.
1 润滑气膜热特性理论模型
新型三瓣式径向气体箔片动压轴承,由轴承套、三瓣波箔和三瓣顶箔组成,如图1 所示.顶箔表面较为光滑,作为轴承的支撑表面,顶箔由波箔支撑为轴承提供适当的刚度与阻尼,且波箔在圆周方向和轴向采用变刚度设计,使得轴承刚度分布更加合理,有利于楔形气膜的形成,能够在一定程度上起到提高轴承稳定性和降低轴承起飞转速的作用.轴承套内侧等间隔地开有3 个燕尾槽,用以安装波箔和顶箔.
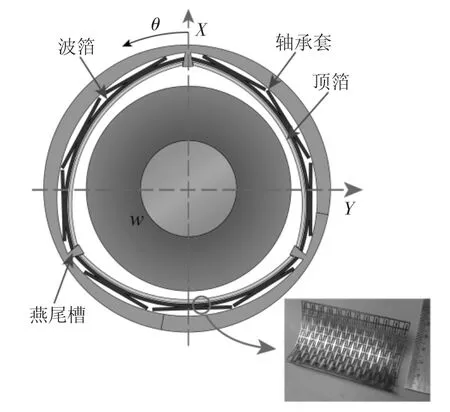
图1 轴承结构示意图Fig.1 Drawing of gas foil radial bearing
在高速旋转机械中,通常采用空心轴设计来减轻转子系统重量.但在高速旋转条件下,随着空心轴壁厚的减小,转子的径向离心伸长量会快速增大,因此在对箔片轴承进行热特性分析时必须考虑转子的离心效应[20];同时,转子的热膨胀量对轴承气膜厚度的影响也不可忽视.在任意圆周方向上,无量纲气膜厚度的表达形式为[21]:
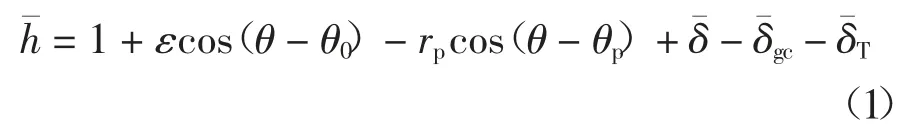
式中:ε 为偏心率;θ0为偏位角(rad);θp为每瓣中心位置对应的角度(rad;δ 为顶箔变形量(m);δgc为空心轴径向离心伸长量(m);δT为空心轴热膨胀量(m);rp为轴承预载;C 为轴承名义间隙(m).
空心轴的径向离心伸长量可通过式(2)进行估算,该方程与有限元分析结果吻合良好[22].
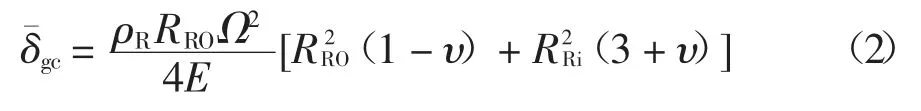
式中:ρR、υ 和E 分别表示转子材料的密度(kg/m3)、泊松比和弹性模量(GPa);RRO和RRi分别表示空心轴的外圆半径(m)和内圆半径(m);Ω 为转子旋转角速度(rad/s).空心轴的热膨胀量可由式(3)进行估算:

式中:αR为转子的热膨胀系数(K-1);Tave为转子的平均温度(K);T0为周围环境气体温度(K).
1.1 考虑热特性的气体润滑模型
1.1.1 非等温Reynolds 方程和能量方程
在对气体箔片轴承进行静动态特性研究时,往往忽略了温度对轴承性能的影响,但转子的高速旋转导致气体在轴承中受到气膜剪切力的作用而使得气膜温度上升,从而造成气体粘度与密度等参数的改变,因此需要求解以下非等温气体Reynolds 方程[23].

在图1 所示坐标系下,适用于气体箔片径向轴承润滑气膜的简化能量方程可表示为[12,24-25]:

式中:x 为气膜圆周方向(m);y 为气膜轴向方向(m);z 为气膜径向方向(m);u 为气体周向流速(m/s);v 为气体轴向流速(m/s);ω 为气体径向流速(m/s);μ 为气体粘度(Pa s);ρ 为气体密度(kg/m3);cp为气体比热容(J/(kg·K));T 为气膜温度场(K);p 为气膜压力(Pa);ka为气体导热系数(W/(m·K)).
在式(5)中,润滑气膜粘度与温度的关系可由Salehi[12]提出的粘温方程表示:

式中:λ=4×10-8;当润滑气膜温度T 的单位为℃时,Tref=-458.75.

要求解上述能量方程(7),需要得到轴承中气膜x、y、z 3 个方向的速度分量.x、y 方向上的速度表达式为:
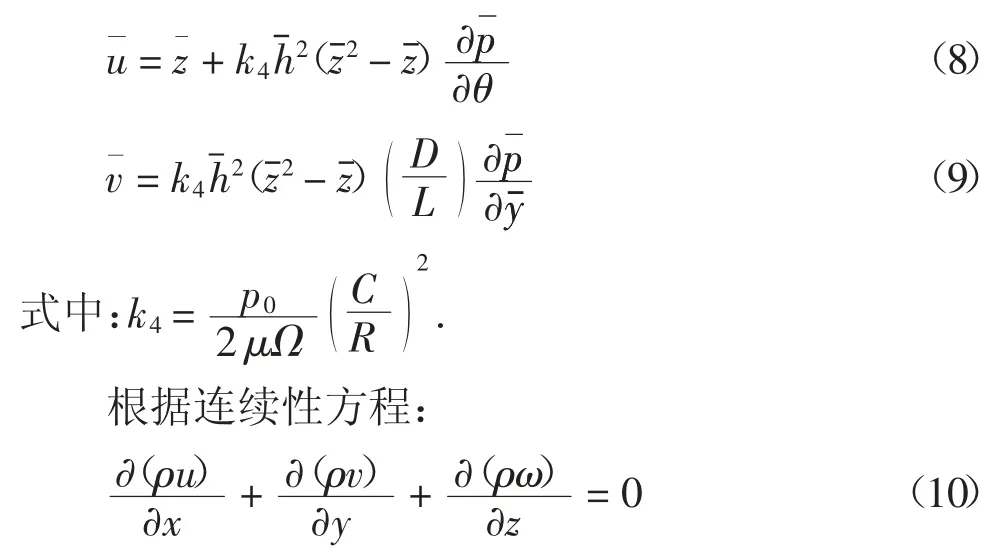
将式(8)(9)代入式(10)可以得到气膜在z 方向上的速度分量:

1.1.2 边界条件
本文通过对轴承的每瓣箔片单独求解、最后整合分析的方式来预测轴承的温度特性.轴承内的气膜分别与转子外表面和顶箔内表面接触,且气膜温度在入口处与进气温度相等,因此能量方程的边界条件可表示为[19]:

式中:θs为每瓣箔片起始的角度位置(rad),等于0、2π/3 或4π/3;Tin为进气口温度(K);TR为转子外表面温度(K);TF为顶箔内表面温度(K).
在式(12)中,气膜在顶箔固定点前缘入口处的温度可由轴承吸入的冷却气流和轴承中循环气流的气体混合能量平衡关系式得到.假设在所属温度范围内气体比热容变化不大,则气膜入口处温度可表示为[24]:
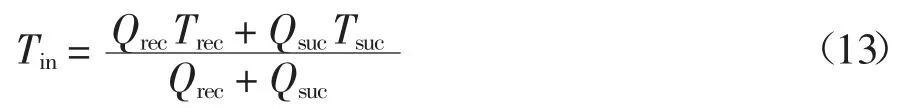
式中:Qrec、Trec分别为循环气体的流量(m3/min)和温度(K);Qsuc、Tsuc分别为吸入气体的流量(m3/min)和温度(K).
随着社会的不断进步,新技术使人类进入了信息传播全球化的时代;它消除了距离的障碍,正十分有效地参与塑造明日的社会[2]。网络课程使学习变得便捷,人们不再需要专门抽空跑到一个固定的地点进行学习,而只需要一台电脑一根网线就可以学到想学习的内容。另一方面来说,由于网络课程的受众广泛,使得学习的成本变低。尤其是当今移动端的兴起,就让这些学习变得更为便利了,只要有时间,拿出Pad或者手机,点开App,就可以进行学习了。
1.2 传热模型
由于转子高速转动,带动气膜粘性剪切耗能产生热量,其中一部分热量会使气膜和各轴承元件升温,另一部分通过顶箔、波箔和热对流的形式传入轴承套并最终扩散到周围环境气体中,以及直接通过转子将热量传递到周围环境中.与轴承的径向和轴向尺寸相比,气膜厚度非常小,因此可以忽略直接通过气膜传递到周围环境中的热量.
1.2.1 箔片传热模型
转子外表面和顶箔内表面温度是气膜温度计算中的重要边界条件,假设转子外表面温度在圆周方向上相等,但由于转子存在偏心,使得每一瓣箔片以及同一瓣箔片不同圆周方向上的温度不尽相同.新型三瓣式径向气体箔片动压轴承箔片结构中的传热路径如图2 所示,其传热可分为箔片内无冷却气流和有冷却气流2 种情况.由于箔片厚度相较于其它方向尺寸很小,可以忽略其在横向上的传热.
当箔片结构中无冷却气流时,一部分热量通过顶箔传导到顶箔与波箔平面平行接触部分,称此接触平面为“第二顶箔”,进而热量传导到第二顶箔与轴承套之间的空气间隙,最终通过轴承套扩散到周围环境中;另一部分热量直接通过顶箔传导到顶箔与轴承套之间的空气间隙中,然后同样通过轴承套将热量传递出去;剩余的热量将通过顶箔与波箔弧形部分的接触区域传导至波箔,通过波箔将热量传导至轴承套并扩散到周围环境中.

图2 传热路径Fig.2 Heat transfer path
当箔片结构中有冷却气流时,一部分热量通过顶箔传导至第二顶箔,最终通过冷却气流传递到环境气体中.由于顶箔部分区域与冷却气流直接接触,这将带走顶箔的一部分热量.其余部分的热量将通过顶箔与波箔弧形部分的接触区域传导至波箔,由于波箔与冷却气流直接接触,波箔结构中的热量一部分通过冷却气流直接传递到环境气体中,另一部分传导至轴承套,并通过冷却气流和环境气体的对流将热量传递出去.
根据图2 所示的传热路径,建立的热阻模型如图3 所示.图3 中TF为靠近顶箔侧气膜温度值,T0为环境温度,各热阻的计算公式如表1 所示.
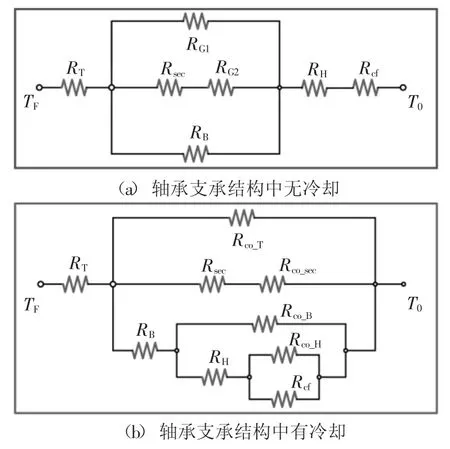
图3 传热模型Fig.3 Thermal transfer model
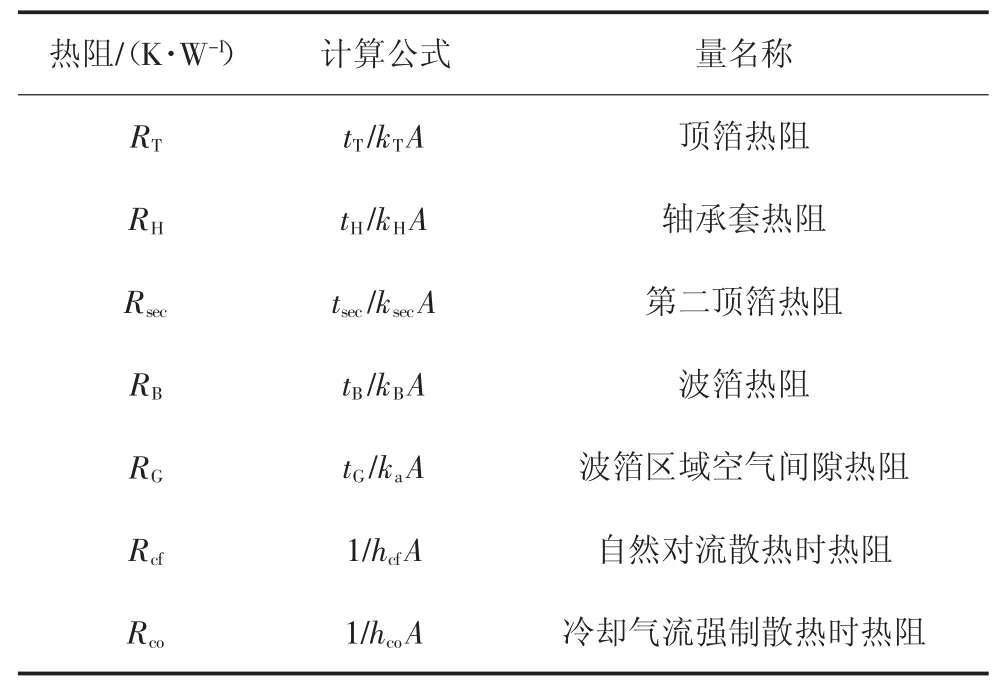
表1 各热阻参数计算Tab.1 Calculation of each thermal resistance parameter
当箔片结构中无冷却气流时,总热阻为:

当箔片结构中有冷却气流时,总热阻为:
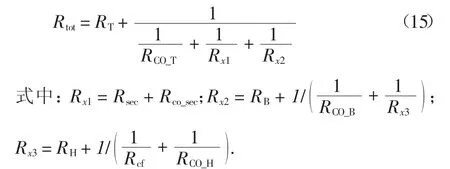
当轴承温度达到稳定状态时,从气膜传递到顶箔中的热量和从顶箔传递出去的热量将处于动态平衡.根据此动态平衡关系,可以建立热平衡方程:

将式(16)无量纲后可得到:

1.2.2 转子传热模型
本文中使用的是空心转子传热模型,部分热量从气膜传导至转子,然后从转子内外表面扩散到周围环境气体中.在任意轴向位置,由于转子的热传导率较高以及转子壁厚较小,可假设转子温度在径向方向上恒定.由于转子高速旋转,可进一步假设转子温度在圆周方向上相等,因此可将转子内的温度情况简化为沿轴向分布的一维温度模型[17-18].各节点的热平衡方程为:

式中:kR为转子导热系数(W/(m·K));Ac为转子的横截面积(m2);TR为转子温度(K);Rin为转子轴厚方向上的热阻(K/W).
空心轴伸出轴承端扩散到周围环境中的热量可表示为[17]:
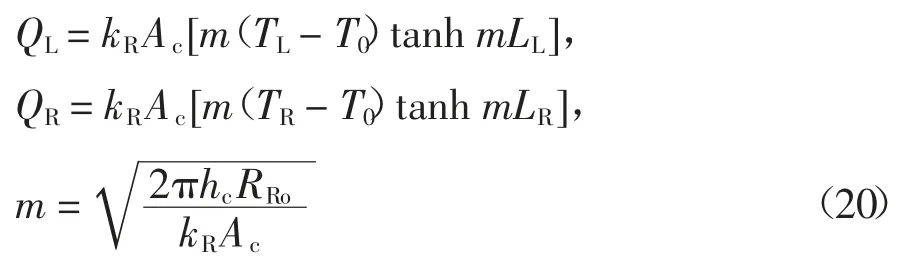
式中:QL为空心轴左侧伸出端流出的热量(W);QR为空心轴右侧伸出端流出的热量(W);TL为轴承左端面温度(K);TR为轴承右端面温度(K);LL为空心轴左侧伸出轴承端长度(m);LR为空心轴右侧伸出轴承端长度(m);hc为空心轴伸出轴承端外表面散热系数(W/(m2·K)).
1.3 计算流程
根据气体箔片径向轴承的非等温Reynolds 方程和能量方程,结合式(12)中的温度边界条件,可得到轴承的气膜温度分布,其计算流程如图4 所示.在给定的转速和外部载荷条件下,通过求解稳态Reynolds 方程,得到转子的初始平衡位置和气膜压力分布.根据初始状态下的压力分布和膜厚分布求解能量方程,得到气膜以及转子的温度分布.在初步温度计算过程中,转子温度视为定值且与环境温度相同,随后在每次的迭代过程中逐步增加转子温度,直到转子热量达到动态平衡状态为止.轴承温度上升会对气膜厚度和气体粘度等参数产生影响,通过求解膜厚方程与粘温方程,并代入Reynolds 方程中重新计算气膜压力与气膜厚度分布.通过将稳态Reynolds 方程和能量方程不断循坏迭代,使前后两次迭代之间的温度和气压差异满足收敛条件,最终得到轴承气膜压力与温度分布.

图4 温度计算流程图Fig.4 Temperature calculation flow chart
2 热特性分析
2.1 轴承气膜压力与温度分布
根据表2 所示的新型三瓣式径向气体箔片轴承参数,可预测出特定工况下轴承温度分布情况,其计算流程见图4.
图5 和图6 分别表示在转速为25 kr/min、载荷为20 N 时轴承的气膜压力与气膜厚度分布.轴承中两瓣箔片之间的间隙较大,可假设箔片在此交界处的气膜压力与大气压力相等,因而在图5 中可以看到气膜压力存在3 个明显的波峰,由于轴承载荷施加于第二瓣箔片所在位置,故压力峰值出现在此瓣箔片上.从图6 中可以看出,由于每瓣箔片气膜压力峰值出现在轴向中间位置处(y=L/2),箔片变形较大,导致最小气膜厚度出现在轴向两侧位置,此外,图中还出现较多尖角毛刺,这是由于箔片局部变形所致.气膜厚度方向中间层的气膜温度分布如图7所示,气膜温度在进气口处快速上升,并在所施加的轴承负载位置(即气膜压力峰值处)的下游达到最大值.从第三瓣箔片的气膜温度分布中可以看出,由于气压下降导致气体发生膨胀,气膜温度也会有所降低.但在前两瓣箔片中,气膜压力峰值距入口处较远且接近出口处,因而没有出现气膜温度下降的情况.
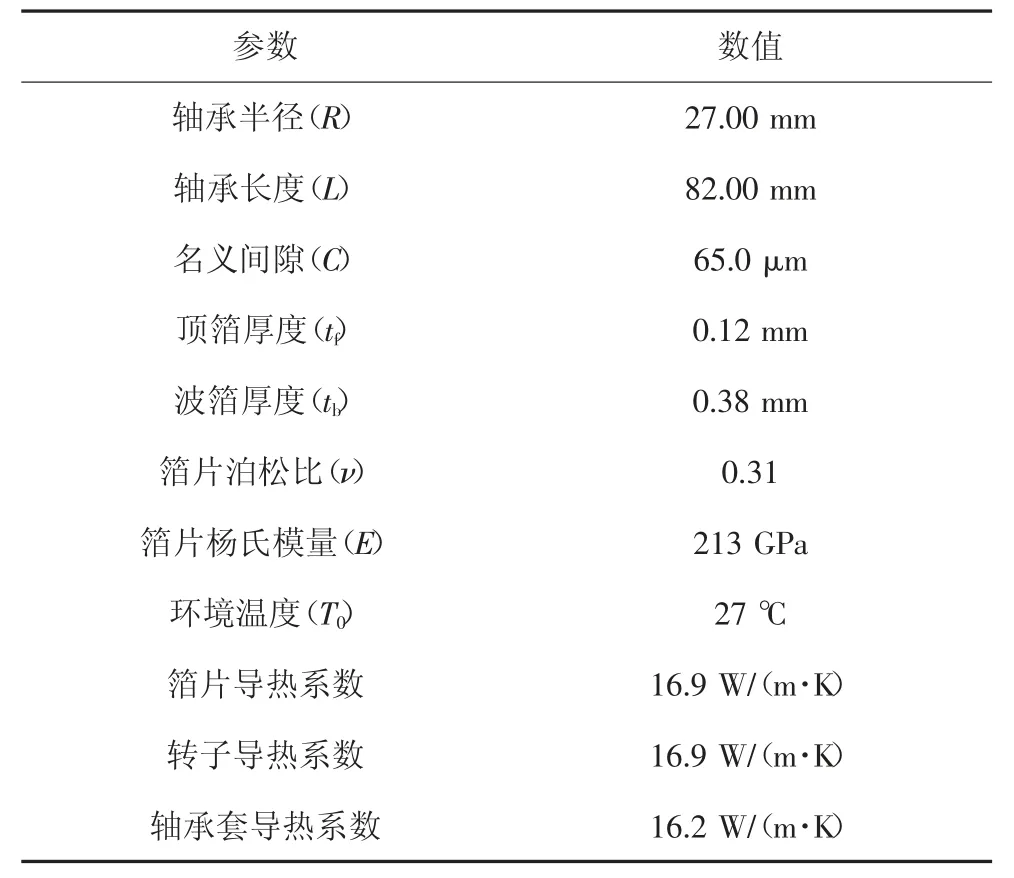
表2 轴承主要参数Tab.2 Gas foil radial bearing main parameters
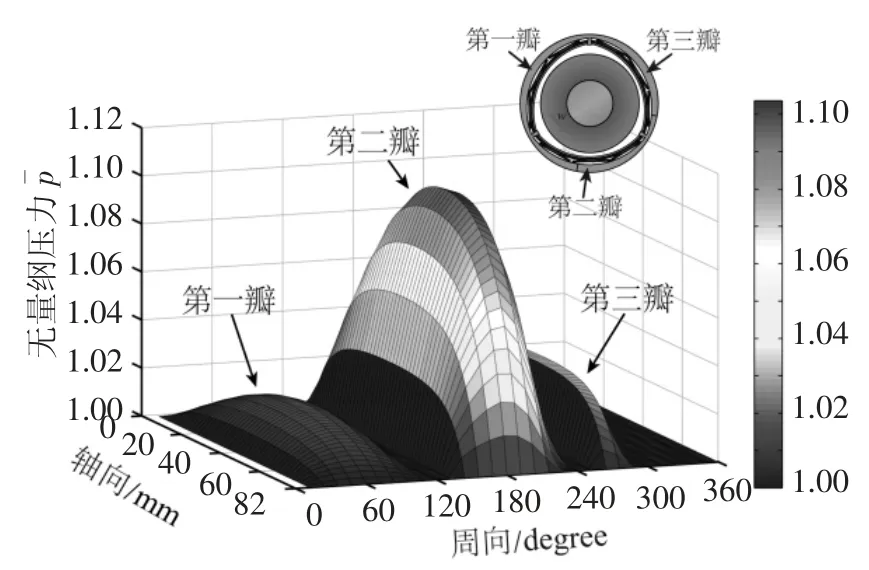
图5 无量纲气膜压力分布Fig.5 Gas film pressure distribution
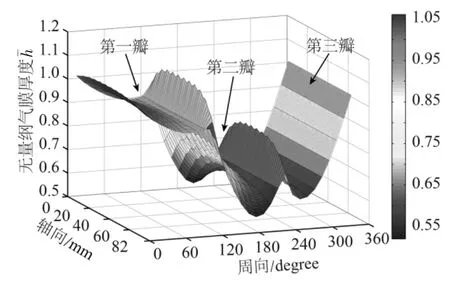
图6 无量纲气膜厚度分布Fig.6 Gas film thickness distribution
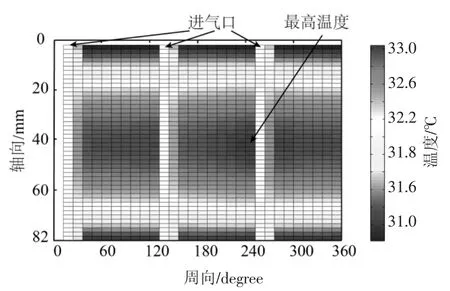
图7 气膜中间层温度分布(Z=h/2)Fig.7 Gas film temperature distribution in(Z=h/2)
图8 表示在上述工况下,轴承轴向中间平面(y=L/2)处气膜温度分布情况,图片上侧表示顶箔内表面,图片下侧表示转子外表面,气膜温度沿转子表面往顶箔侧逐渐上升,在顶箔侧所施加轴承负载位置的下游处达到峰值.
如1.2.2 节中所述,假设转子温度在圆周方向上相等,并将转子内的温度情况简化为沿轴向分布的一维温度模型.在转速为25 kr/min、载荷为20 N 时转子的轴向温度分布如图9 所示,转子温度沿轴向呈抛物线分布.

图8 气膜轴向中间截面温度分布(y=L/2)Fig.8 Gas film temperature distribution in y=L/2
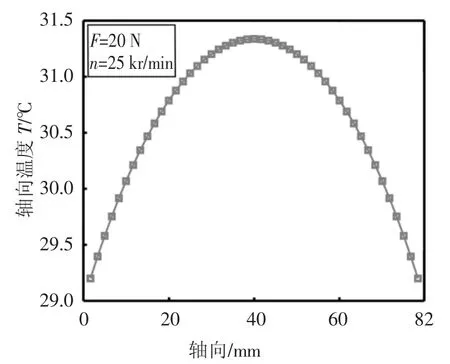
图9 转子轴向温度分布Fig.9 Rotor temperature distribution in axial
2.2 转速与载荷对轴承温度的影响
图10 表示轴承最高温度与转子转速之间的关系,所施加的载荷为20 N.从图中可以看出,当转速从15 kr/min 增加到40 kr/min 时,气膜的粘性剪切耗能不断增加,气膜与转子最高温度随转速的上升几乎呈线性递增,且随着转速的不断增大,气膜与转子之间的温度差值也在不断增加.为研究转速对不同箔片气膜温度的影响,在载荷为20 N 的情况下,分别取转速为20 kr/min、30 kr/min 和40 kr/min,取各箔片中的气膜最高温度作为分析参数,如图11 所示.由图11 可知,各箔片的最高温度随转速的上升而递增.由于第二瓣箔片作为主要承载面,产生的气膜压力相对较高,因此在同一转速条件下,第二瓣箔片中的气膜温度会高于其他两瓣箔片.
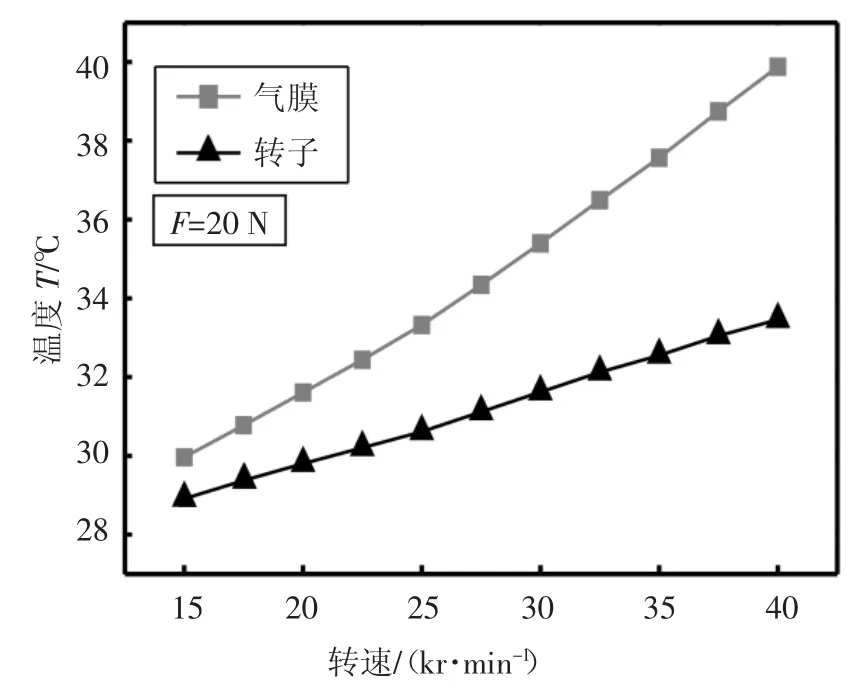
图10 转速对轴承最高温度的影响Fig.10 Effect of speed on the maximum temperature of the bearing

图11 转速对各箔片最高温度的影响Fig.11 Effect of the speed on the maximum temperature of each foil
图12 表示轴承最高温度与轴承载荷之间的关系,转速为25 kr/min.从图12 中可知,气膜和转子最高温度几乎不随载荷发生变化,当载荷从10 N 升至40 N,温度变化在1 ℃以内.对比图10 和图12 可发现,相较于转速对气膜温度的影响,轴承载荷的影响并不明显.载荷对各箔片的温度影响如图13 所示,转速为25 kr/min,分别取载荷为20 N、30 N 和40 N.与转速的影响相似,各箔片最高温度随载荷的增加而略微上升,且第二瓣箔片的温度上升最大,可见载荷对主要承载箔片的温度影响最为显著.
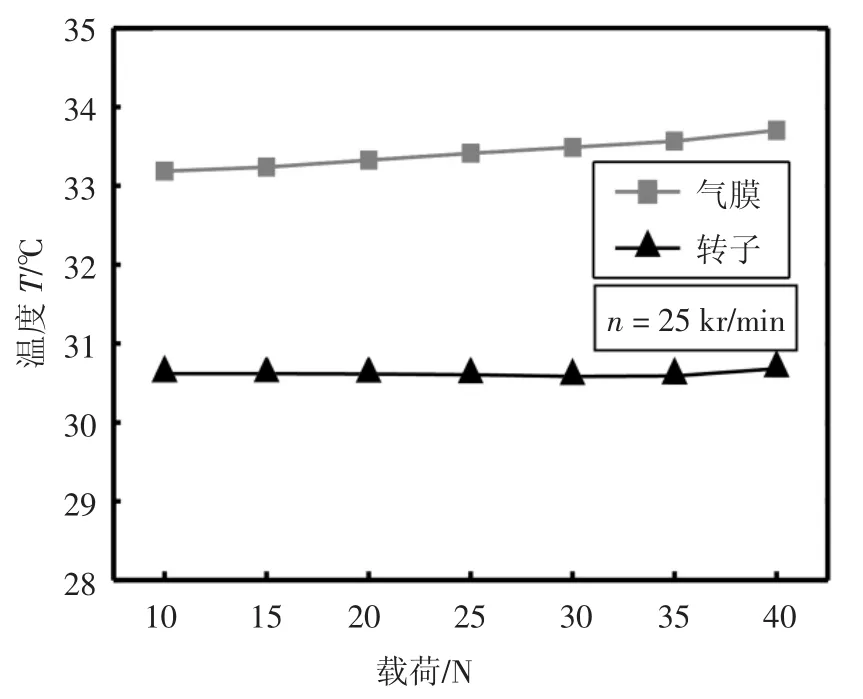
图12 载荷对轴承最高温度的影响Fig.12 Effect of load on the maximum temperature of the bearing
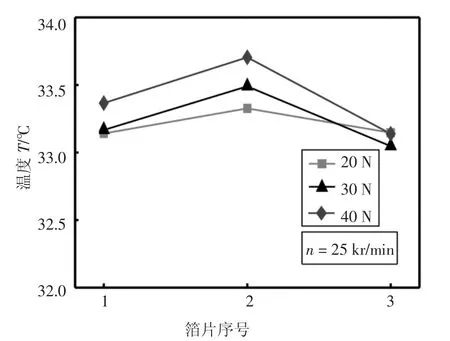
图13 载荷对各箔片最高温度的影响Fig.13 Effect of load on the maximum temperature of each foil
2.3 冷却气流对轴承温度的影响
图14 表示的是在箔片内不通冷却气流和通入1 m3/min 的冷却气流时轴承温度随转速的变化,冷却气流温度与环境温度相同,载荷为20 N.从图14 中可以看出,当在箔片结构中通入冷却气流时,气膜和转子温度都将显著下降,且随着转速的上升,冷却气流对轴承的降温作用越来越显著.在工程实际应用中,建议采用通入冷却气流的方法对箔片轴承进行温度控制.
为分析不同冷却流量大小对轴承热特性的影响,计算参数设为轴承载荷20 N、转速25 kr/min,如图15 所示,且冷却气流温度与环境温度相同.从图15 中可以看出,随着冷却流量的增加,气膜和转子最高温度先快速下降,然后趋于稳定,即当冷却流量增加到一定大小时,再增大流量不会对轴承温度有显著影响,气流对轴承的冷却已达到饱和状态.

图14 不同冷却条件下轴承最高温度与转速的关系Fig.14 Relationship between maximum bearing temperature and speed under different cooling conditions

图15 冷却气流量对轴承最高温度的影响Fig.15 Effect of cooling gas flow on the maximum temperature of the bearing
2.4 轴承温度对承载力的影响
轴承温度的变化会改变轴承中的气体粘度和密度等参数,而这些参数的改变又会对轴承静态性能造成影响.为研究温度变化对轴承静态性能的影响,取载荷为20 N,分析在非等温情况下偏心率随转速的变化情况;取转速为25 kr/min,分析在非等温情况下偏心率随载荷的变化情况,结果分别如图16 和图17 所示.由图可知,等温模型假设气膜温度不发生变化,且与周围环境温度一直保持相同,转子偏心率随转速的上升而下降.在相同的工作条件下,即轴承载荷与转子转速相同时,由于气体粘度随轴承气膜温度的上升而增加,与恒温条件下相比考虑轴承温度效应时的偏心率会更低,可见,忽略轴承温度变化将低估轴承承载能力.当考虑温度对气体粘度和密度的影响时,轴承运行环境将更加符合实际情况,从而更加精确地预测轴承静态性能.
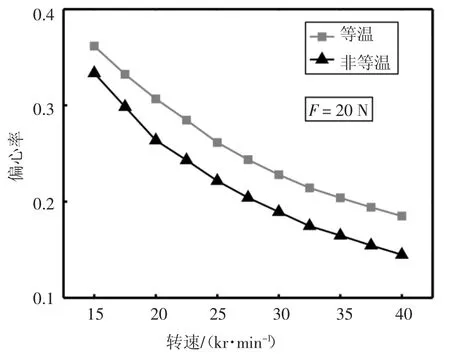
图16 非等温和恒温条件下偏心率与转速的关系Fig.16 Relationship between eccentricity and rotational speed under non-isothermal and isothermal conditions

图17 非等温和恒温条件下偏心率与载荷的关系Fig.17 Relationship between eccentricity and load under non-isothermal and isothermal conditions
3 结论
针对新型三瓣式径向气体箔片动压轴承,提出了相应的整套热特性润滑理论模型.通过耦合求解非等温Reynolds 方程和气膜能量方程,并考虑转子的离心效应和热膨胀量对轴承温度的影响,运用数值模拟的方法求解出气膜温度分布.通过详细分析气膜温度分布特征和主要参数对轴承温度的影响,得出以下结论:
1)气膜温度在进气口处快速上升,并在所施加的轴承负载位置的下游达到最大值,且沿转子表面往顶箔侧气膜温度逐渐上升,高温区域分布在接近顶箔侧的位置,因此在箔片结构中通入冷却气流可以起到更好的降温效果.
2)转子温度沿轴向呈抛物线分布.
3)各轴承元件温度随转速线性递增,且随着转速的上升,气膜与转子的温度差值不断扩大.相较于转速对气膜温度的影响,轴承载荷的影响并不明显.
4)往轴承箔片结构中通入冷却气流可以起到明显的降温效果,且随着转速的上升,冷却气流对轴承的降温作用越来越显著.
5)等温模型将低估轴承承载能力,与等温模型相比,非等温模型可更加切合实际的预测轴承静态性能.
