双曲率蜂窝夹层壳单模态动力响应数值仿真

李 洁

(宿迁学院 建筑工程学院,江苏 宿迁 223800)

0 前 言

蜂窝夹层结构质量轻，用料省，强度大，刚度强，还具有较好的隔热性和隔振性，是一种特殊的复合材料，广泛应用于航空航天、建筑行业、海洋结构等领域。比如：长征三号甲火箭的卫星整流罩，大厦的帷幕墙、屋顶，飞机的机翼、雷达罩、进气道等都应用了蜂窝夹层结构，可见，对蜂窝夹层结构的静、动力学分析具有很大的实用价值。但是从查阅的文献表明，很少有人对蜂窝夹层壳体进行动力学分析，几乎都是集中在蜂窝夹层板的研究。本文建立了四边简支双曲率蜂窝夹层薄壳单模态运动微分方程，利用R-K法给出了不同激振力频率及不同激振力幅值下强迫振动的动力响应曲线。

1 模型简介

双曲率薄壳模型由上下蒙皮以及中间形如蜂窝的六边形胞元层芯组成，层芯等效为一正交异性层，四边受到简支约束，x1和x2两个方向的弧长分别用a1和a2表示，曲率半径分别用R1和R2表示，蜂窝夹层厚度为tc，整个壳体的厚度为t，受横向激振力S=Fcosωt，考虑蜂窝夹层壳体的几何非线性以及小变形理论，应变与位移的关系应该为：

(1)

不考虑夹层壳体中面各点的位移，Reddy三阶剪切变形理论给出了壳上任意一点(x1,x2,z)在壳体变形后的位移函数[2]。应用能量守恒和Hamiton变分原理可以得到：

(2)

式中，激振力的作用位置为x01，x02；dA为壳体的微元面积；R为面积积分区域。将式(1)及每一层的应力应变关系[3]代入式(2)，分别提取δw0、δθ1、δθ2的系数即可得到双曲率蜂窝夹层壳强迫振动的运动微分方程。

2 蜂窝壳体单模态的动力学方程

单模态下四边简支的位移函数表示为：

(3)

如若只考虑横向的弯曲振动，将式(3)代入强迫振动的运动微分方程，分别积分后，得到单模态下夹层壳体的动力学方程：

(4)

式中，F′=4a1a2F/π2；M′、K′分别为考虑非线性之后系统的质量矩阵和刚度矩阵。M、K为线性情况下的质量矩阵以及刚度矩阵[4]，两者之间的关系为：

M′11=M33、M′12=M34，M′13=M35，M′21=M43，M′22=M44，M′23=M45，M′31=M53

M′32=M54，M′33=M55

由于只考查横向振动，在略去小项，考虑进阻尼的情况后，单模态下夹层壳体的动力学方程可简化为一单自由度的微分方程：

(5)

3 数值仿真

利用R-K法对双曲率皆为0.01，弧长皆为1 m的蜂窝夹层壳体进行了单模态下的动力学分析。其中tc/t=0.87，t/a=0.01，芯层胞元的长度4×10-3m，角度300，厚度2.54×10-5m，阻尼比为0.01，铝制蜂窝夹层壳的弹性模量为68.9 GPa，泊松比为0.03，密度2 768 kg/m3。对动力学方程进行数值计算，给出了激振力幅值在100 N时，激振力频率分别为20、400 Hz下的动力响应以及激振频率在50 Hz时，激振力幅值分别取1、4 kN时的动力响应。图1为ρ=100 N时，系统在不同的激振力频率下的动力响应曲线，图2为w=50 Hz时，不同激振力幅值下系统的动力响应曲线。

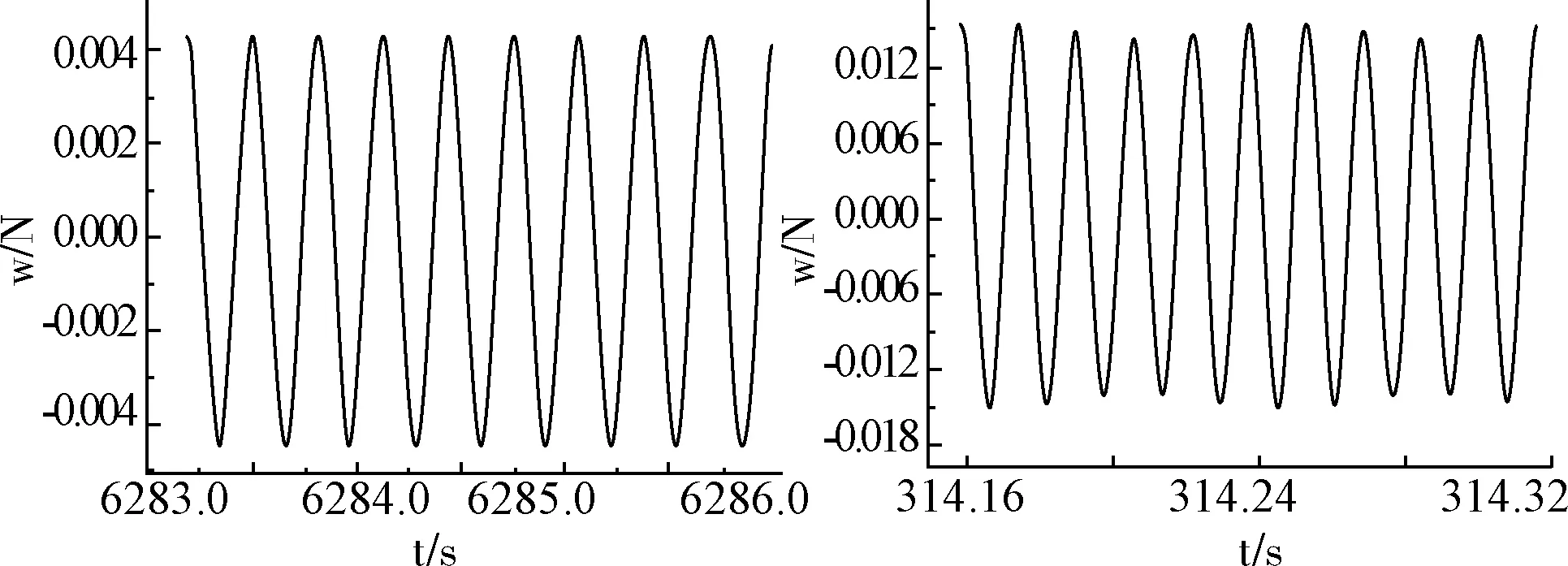
图1 p=100 N时，系统在不同激振力频率下的动力响应曲线

图2 ω=50 Hz时，不同激振力幅值下系统的动力响应曲线

4 结 论

图1表明激振力幅值在100 N时，激振力频率在20 Hz时，蜂窝夹层壳体呈单倍周期运动，当激振力频率增大到400 Hz时，呈现的是5倍周期运动，并且随着频率的不断增大，系统的振幅也在不断增大。图2表明，激振力频率在50 Hz(远离固有频率)[3]时，随着激振力的幅值增加，系统动力响应从单倍周期运动变换到三倍周期运动，振幅也在变大。

[ID:010357]