基于MIDAS GEN的单层球面网壳稳定性分析

2020-10-31董自勇

四川建材 2020年10期

董自勇

(四川省建筑科学研究院有限公司，四川成都 610081)

0 前言

现阶段，大跨度空间结构较为流行，广泛运用于建筑项目中。其中，单层网壳结构是主要类型，其具有刚度高、重量轻等优势，再加上三维受力及空间性状等显著特征，能够跨越更广阔的空间，可对各种建筑功能及造型需求予以有效满足，备受关注。大跨度单层网壳因折算厚度较低，当结构需承受较大力量时极易出现位移情况，二阶效应则无法采取传统计算法，如此失稳模态整体性较差，越跃屈曲产生风险较大，这样以来，以构建稳定计算长度法则难以满足《钢结构设计标准》(GB50017—2017)[1]各项标准。对于这一情况，笔者建议采用二阶P-Δ和P-δ效应，并同时采取初始缺陷的直接分析法，对不同负荷影响下所出现的位移及内力数据进行如实测量，无需采取长度法来验算构建受压稳定性。现阶段频繁使用有限元分析软件，其主要包括了ABAQUS、SAP2000、MIDAS GEN等。本研究以某图书馆单层球面网壳屋盖为研究对象，采取MIDAS GEN 2018全面分析了其稳定性，并通过屈曲模态分析、非线性分析其网壳。通过研究证实，这一种网壳符合稳定性承载力有关规定，为类似结构的分析和设计提供有益参考。

1 工程概况

本工程项目为某图书馆单层球面网壳屋盖(见图1)，球面跨度为42.5m，矢跨比为1/5。径向肋梁主要采用250 mm×150 mm×10 mm的矩形钢管，环向肋梁150 mm×150 mm×5×8 mm、100 mm×100 mm×5 mm的矩形钢管，斜杆支撑主要采用76 mm×4 mm的圆钢管，材质均采用Q235B钢材。

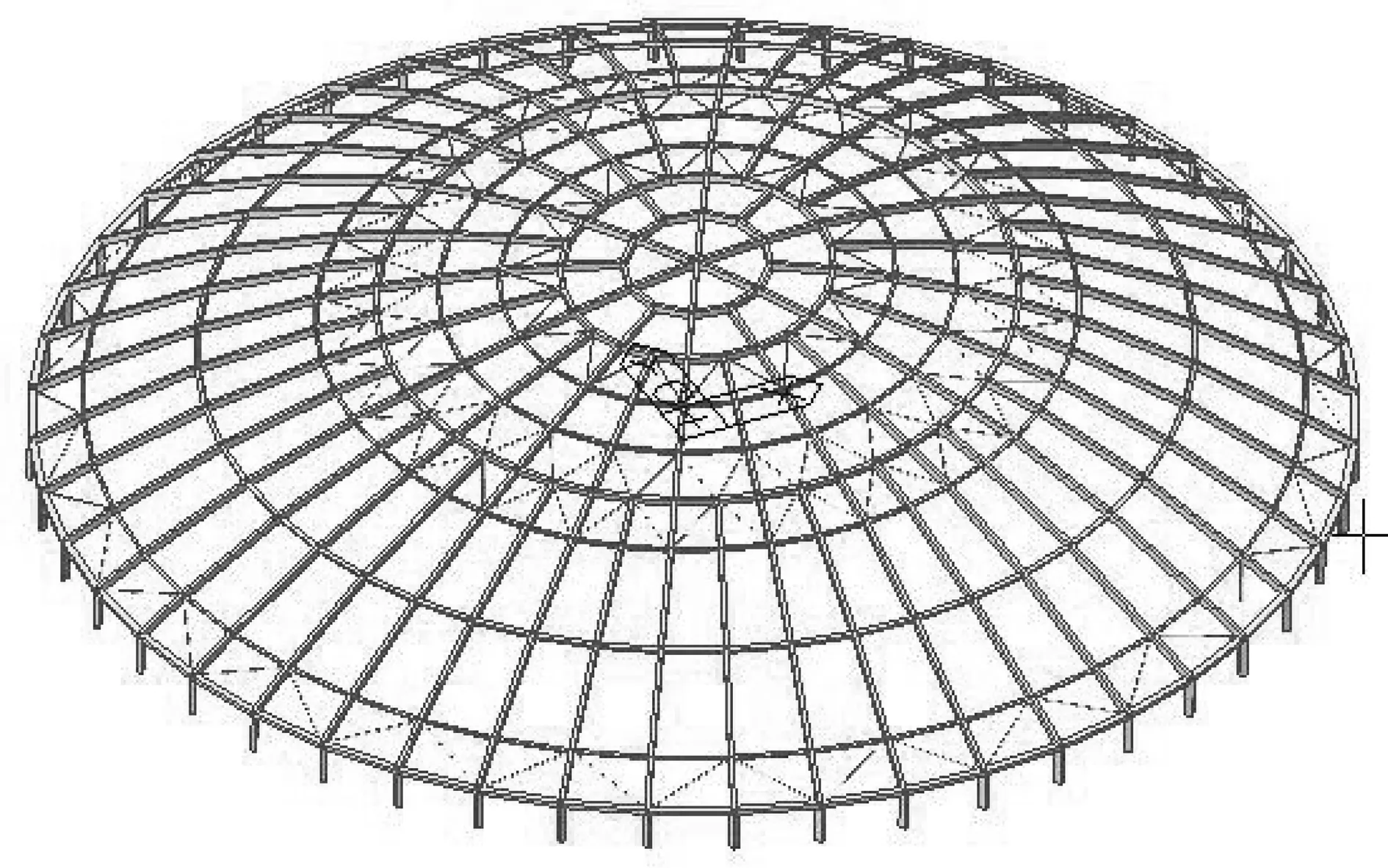
图1 计算模型三维图

2 稳定性分析理论

2.1 屈曲模态分析

研究稳定性前，对于单层网壳应接受屈曲模态分析(重点分析其弹性稳定性)[2]。对此，本研究采取有限元法，方程式如下：

(K-λK0)Δ=0

(1)

式中，K为结构刚度矩阵；K0为结构几何刚度矩阵或结构初始应力矩阵；λ为一种特征值，表示荷载模式的比例因子；Δ为一种特征向量，即屈曲模态中各节点的模态向量。

根据以上公式计算出临界荷载系数、特征向量，其中临界荷载计算方式为：荷载初始值×临界荷载系数；特征向量则是临界荷载的屈曲模态，如果荷载已经要抵达临界荷载时，结构便会出现同模态相类似的屈曲。

2.2 非线性稳定分析

总所周知，对于结构而言，无论是几何原因，还是材料原因，均会产生非线性性质，为了能够符合同实际设计规定相一致的网壳结构承载力，参照《空间网格结构技术规程》(JGJ 7—2010)[3]，单层网壳结构需接受整个过程的非线性屈曲分析，则是将一定量的外部荷载作用于网壳，且不断增加荷载，对网壳变形情况进行重点观察。因随着荷载不断增加，网壳变化越来越严重。对于此情况，可重点考虑结构具有几何非线性特征。同时，网壳主要采取钢材，屈服是其典型特征，当需承受塑性变形荷载时，则出现了非线性变化，其实质则是材料非线性。以非线性有限元分析为切入点的结构荷载-位移全过程，能够清楚地呈现出结构刚性、稳定、强度等特征变化的全过程。

2.3 初始几何缺陷

单层网壳类同承受面外荷载薄壁结构较为相似，针对初始缺陷感到特别敏锐，一点点的节点偏差则会严重影响结构的稳定性。在项目实践活动中，往往因施工精度、生产技术等因素造成网壳出现偏差情况(例如杆件初始应力、杆件初始弯曲、节点坐标偏差等)[4]。因此，采取结构的最低阶屈曲模态来细致分析初始几何缺陷分布情况，基于网壳跨度的1/300计算出缺陷最大值。

3 整体稳定性分析

针对网壳稳定性而言，可从恒荷载DL、活荷载LL、两种风荷载W等方面的荷载情况进行分析。分析结构稳定性时，一般不得将地震、温度荷载等因素纳入考虑范围中。

3.1 屈曲模态分析

分析该项目模态时使用MIDAS GEN 2018有限元分析软件，可迅速查找到失稳最明显的荷载组合，如图2～3所示。

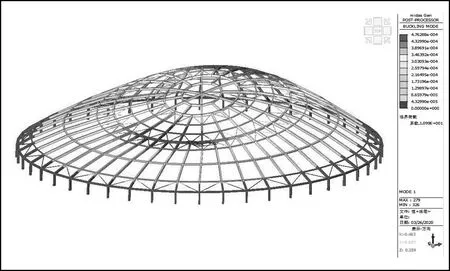
图2 荷载组合1(1.0DL+1.0LL)的第一阶屈曲模态图

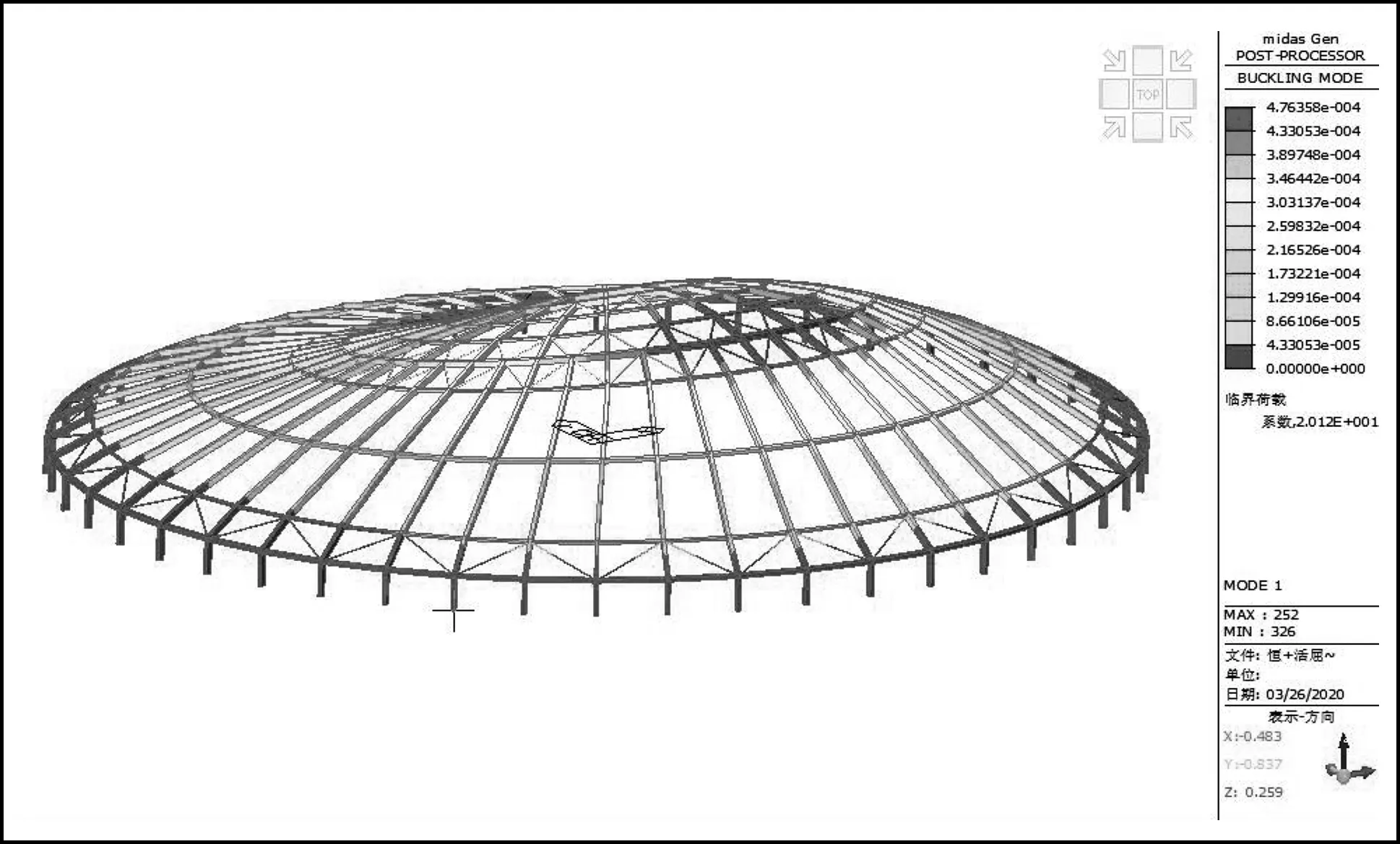
图3 荷载组合1(1.0DL+1.0W)的第一阶屈曲模态图

模态分析的临界荷载系数，其实质是网壳稳定极限承载力同网壳稳定容许承载力的比例值，需满足《空间网格结构技术规程》(JGJ 7—2010)中各项指标。以上荷载组合1(1.0 DL+1.0 LL)最小临界荷载系数为10.99，这充分反映了该项目结构在这一荷载组合影响来失稳风险最大。对于这一荷载组合，最好还需分析其初始几何缺陷情况，并构建相对应的模态，这便是弹性稳定分析[3]。

3.2 考虑初始几何缺陷的模态分析

针对这一项目实际情况，最大跨度42.5 m，1/300则是142 mm，因此,该项目初始几何缺陷最大计算值则是142 mm。针对失稳风险最大的荷载组合1，通过分心屈曲模态后，准确计算出屈曲向量最大点的屈曲向量值，并将初始缺陷最大值与屈曲向量最大值比例找出，全部屈曲向量×比例值，找到每一个节点的初始缺陷，并把这些缺陷同原先对应的节点坐标进行重叠，对这些节点坐标进行相对于的改变，这便是初始缺陷的网壳模型。

对于初始几何缺陷分析后，荷载组合1第一阶屈曲模态如图4所示。这一临界荷载系数10.82，相比于初始缺陷10.99偏小，可不予考虑。但是这一数值依然符合JGJ7—2010相关条款“在分析弹性全过程、单层球面网壳、柱面网壳和椭圆抛物面网壳时，安全系数K应确定为4.2”。

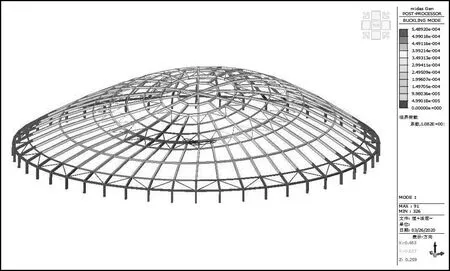
图4 考虑初始缺陷后荷载组合1的第一阶屈曲模态图

3.3 非线性稳定分析

因荷载组合量较大，对其进行全部分析完全没有必要。实际上，选取屈曲模态临界荷载系数最低的荷载组合1予以重点分析即可。把荷载组合1确定为一个单独的非线性荷载工况(FXX)，开展弹性分析，确定竖向变形最大的节点(节点号为306)，非线性分析其位移控制点，如图5所示。

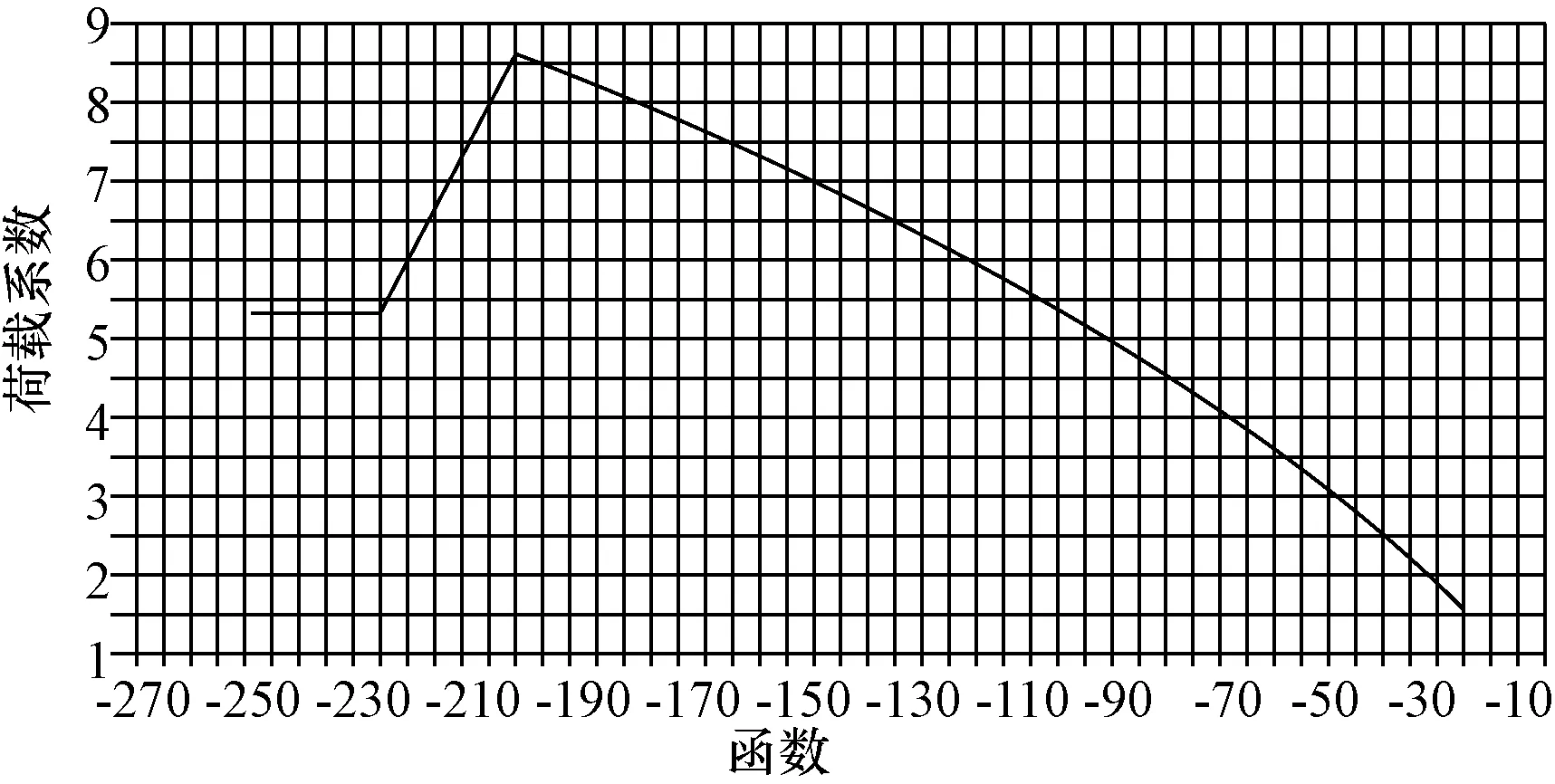
图5 几何非线性分析结果曲线

图5中，荷载系数最大值为8.59，出现在-200位置；荷载系数最小值为1.55，出现在-25位置。结果显示：①当荷载增加到荷载标准值的七倍后，刚度退化情况十分明显；②结构极限荷载到达荷载标准值8.59倍时，便符合《空间风格结构技术规程》(JGJ7—2010)中“在分析弹塑性全过程分析、且为单层球面网壳、柱面网壳和椭圆抛物面网壳时，安全系数K为2.0”的规定条款[5]。