微重力条件下上面级贮箱液体推进剂自由界面变形数值模拟研究

肖立明，李 欣，胡声超，刘 畅，周炳红

（1. 北京宇航系统工程研究所，北京 100076； 2. 中国科学院 国家空间科学中心，北京 100190）

0 引言

液体火箭上面级在飞行过程中，经常关闭主发动机进行空间惯性飞行（微重力滑行）。为保证滑行一段时间之后主发动机顺利再启动，一般在微重力滑行期间采取姿控发动机沉底或者推进剂管理装置等来解决推进剂管理问题[1-2]。上面级贮箱内同时存在液体推进剂和增压气体，研究微重力条件下气液自由界面在不同加速度条件下的变形过程以分析贮箱内气液两相的运动状态，是推进剂管理涉及的关键内容之一。

微重力流体管理不仅应用在火箭上面级，也应用在卫星的变轨和调姿过程。落塔微重力试验是微重力流体管理研究的重要验证方法，可通过试验获取重定位过程中的推进剂沉底时间，进而确认推进剂管理方案是否可行[3-5]，但其存在周期长、成本高的不足[6]。数值模拟研究可以自主加载边界条件，对比落塔试验更长的时间范围进行分析，因此日益得到重视。赵志建等[7]和王毅等[8]采用最小能量法对自由界面的平衡形态进行数值模拟，但未考虑自由界面变形的动力学过程，只计算了最终的自由界面平衡形态。刘春辉[9]利用VOF-3D 软件计算微重力条件下40%充液旋转贮箱中的液体再定位过程，再现了推进剂沉底过程中的喷泉现象，得到的流型与实验结果一致，显示了数值模拟方法的准确、有效。

上面级贮箱在尺寸、形式、材料、推进剂以及微重力条件等方面均与传统的卫星贮箱存在一定差异，导致其推进剂管理方案明显不同于卫星贮箱的。国内目前在微重力流体管理方面的研究主要集中在卫星贮箱应用上，对上面级贮箱的相关研究较少。陈健等[10]近年来开展了关于火箭液氧贮箱缩比模型的实验研究和相应的数值模拟研究，但数值模拟采用的是二维有限元方法，未考虑表面张力效应的影响。

本文采用数值模拟方法，研究某上面级液氧贮箱在微重力滑行段自由界面的变形过程，预示液氧贮箱内的典型流体运动形式，并与理论值进行对比分析。

1 研究对象及数学模型

本文所研究的上面级液氧贮箱如图1 所示，贮箱关于z 轴呈旋转对称形状，中间柱段高0.8 m，半径r 为1.5 m；上、下底为椭球形，长轴长1.5 m。贮箱中上半部分增压气体为氦气，下半部分液体推进剂为液氧。液氧与贮箱壁面的接触角为θc，液氧表面张力系数为σ，受到的加速度为a。

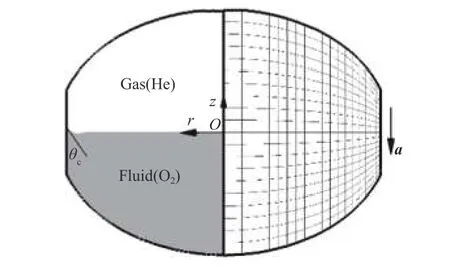
图1 液氧贮箱结构示意Fig.1 Schematic diagram of liquid oxygen tank

本文采用流体体积法（VOF 方法）[11-13]求解液氧贮箱内推进剂的运动及自由界面的变形。VOF方法由Hirt 和Nichols 于20 世纪80 年代提出，目前已成为研究自由界面问题最主要的方法，被引入到商业软件Fluent 中，可以很好地解决自由界面的变形问题。李章国等[14]已将该方法成功用于气液自由界面的数值模拟。

假设流动为不可压缩黏性层流流动（气体流速很低，可以考虑为不可压缩流体），则流体连续性方程、动量方程和流体体积函数的控制方程可以表示如下：

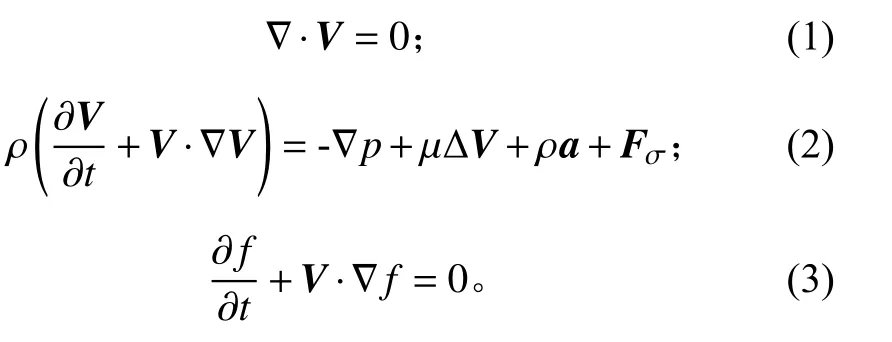
式(1)～式(3)中： V为流体运动速度；ρ 为流体密度；p 为流体压力；μ 为流体运动学黏性系数； Fσ为流体表面张力的等效体积力形式；f 为流体体积函数，定义为每个空间单元内流体所占体积与该单元可容纳流体体积之比。

本研究中，流体运动速度在贮箱壁面上满足无滑移条件，即

其中 Vw为贮箱壁面的运动速度。

流体体积函数在壁面上满足接触角条件

本文需求解的问题是非定常问题，初始条件为流体静止，流体界面保持为平面。

2 理论分析

液体爬升和表面张力波是经典流体力学的重要内容，具体推导过程可参考流体力学教材[15]。

1）液体爬升高度

对于初始水平的液面，液体在表面张力作用下将沿容器壁面爬升一定高度，达到静力学平衡。在一个大的容器中，液体界面爬升高度h 和特征毛细长度d 之间的关系可表示为

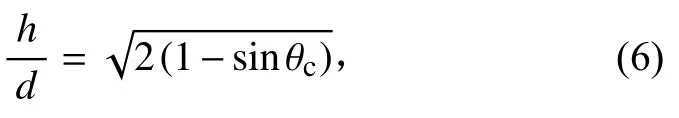
2）表面张力波的色散关系

考虑表面张力作用的线性浅水波色散关系可表示为

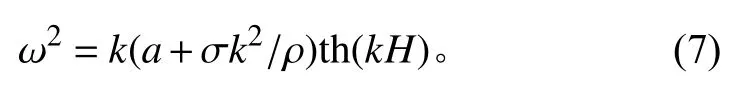
式中：ω 为圆频率，ω=2π/T，T 为波动周期；k 为波数，k=2π/λ，λ 为波长；H 为水深。

由该色散关系可以求出波包传播的群速度U=dω/dk。

3 数值模拟

采用流体体积法对控制方程进行离散处理，利用物理量守恒构建差分方程。鉴于研究对象本身的对称性，选用二维轴对称模型进行计算。采用适体坐标系网格，网格数为160×160。非定常项采用全隐式格式，对流项采用QUICK 格式，扩散项采用中心差分格式。这样就保证了整个离散方法的二阶精度。

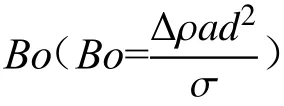
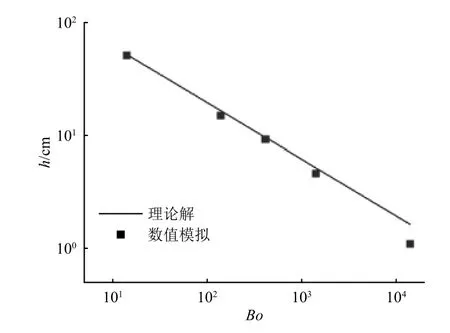
图2 液体爬升高度h 随邦德数Bo 的变化Fig.2 The liquid climbing height h against the Bond number

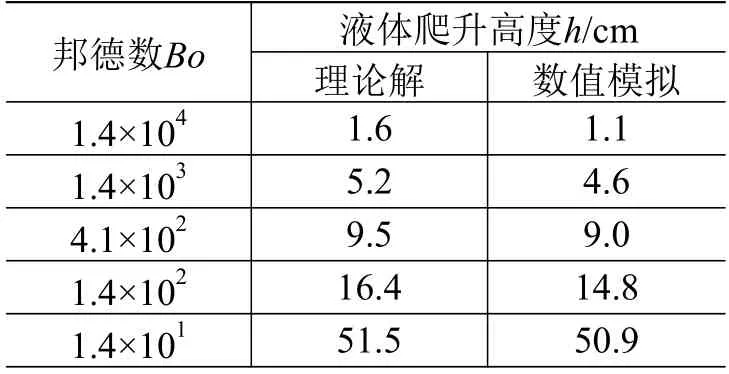
表1 液体爬升高度理论解与数值模拟对比Table 1 Theoretical and numerical simulation results of liquid climbing height

4 数值模拟结果分析

数值模拟得到的Bo 为140、14 和0 时的自由界面变形过程分别对应表面张力波、沃辛顿喷射和气泡形成3 种不同的典型流体运动形式。

1）Bo=140（表面张力波）

当邦德数较大时，自由界面的变形过程表现为表面张力波形式。图3 显示了邦德数为140 时自由界面变形过程的主要特征。初始时刻（t=0 s）液氧界面为平面，体积为容器容积的一半。之后，在表面张力作用下，液氧沿壁面往上爬升，形成对平整液面的扰动。该扰动包含有各种波长（波数）的模态，t=40 s 时，之前的1 个大波包发展成2 个明显的波包。然后各波包由壁面向容器中心传播，波数较大（波长较小）的波包传播速度较快，这与式(7)和流体力学波动理论的结论相一致。小波长波包先到达中心位置，接着大波长波包于t=120 s 时到达中心；先形成一个小气泡，之后气泡消失，液体向上喷涌，但幅度不大，没有发生破碎现象；最后液面逐渐恢复平静。

图3 邦德数为140 时的自由界面变形过程Fig.3 Free surface deformation process for a Bond number of 140

最终液面爬升高度稳定在0.148 m 处，图3 中大波包的波数为12.27/m，群速度为0.012 5 m/s。由流体力学理论可以算出液面爬升高度为0.164 m，群速度为0.012 2 m/s。可见数值模拟结果和理论解比较接近，说明本文的数值模拟结果正确。

2）Bo=14（沃辛顿喷射）

当邦德数减小时，液面爬升高度增加，表面波的振幅加大。图4 显示了邦德数为14 时自由界面的变形过程。表面波传播规律与邦德数为140 时基本相同，大波包在大约t=180 s 时传到中心位置，比邦德数为140 时要晚。这是由于邦德数较小时，液面爬升高，扰动强，波数小，所以波包群速度也更小，传播时间就更长。与邦德数为140 时情况不同的是，在t=300 s 时波包在反弹之后发生了破碎，形成了流体力学中的沃辛顿喷射现象。

3）Bo=0（气泡形成）

当邦德数为0（此时加速度也为0），即上面级作自由滑行时，自由界面变形进一步加大（见图5）。t=360 s 时开始，液面在贮箱内形成一个完整的气泡。这是由于表面张力作用下，液面不断收缩，表面能不断减小，最终达到一个表面能最低的平衡状态。

图4 邦德数为14 时的自由界面变形过程Fig.4 Free surface deformation process for a Bond number of 14

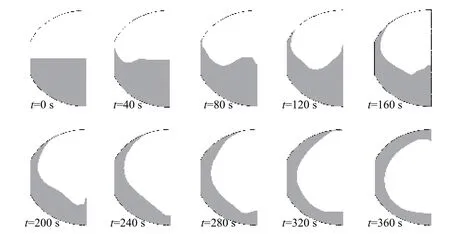
图5 邦德数为0 时的自由界面变形过程Fig.5 Free surface deformation process for a Bond number of 0

贮箱内的液氧液面形成完整的气泡将直接威胁到主发动机二次点火的成功。不过，由于完整气泡的形成需要长达360 s 的时间，故可以考虑在100～200 s 时施加沉底推力，使液面重新恢复平整，然后再撤除沉底推力，即采用脉冲式流体管理。

从以上计算结果来看，脉冲式流体管理技术具备可行性，但是，具体参数还需相应的数值模拟和试验来确定。

5 结束语

本文采用流体体积法对微重力条件下上面级贮箱内液氧推进剂自由界面变形过程建立了完整的数学模型，针对不同邦德数条件进行了数值模拟，得到的液体爬升高度和表面张力波传播速度与流体力学理论符合较好，证明该数值模拟方法可行。并通过数值模拟再现了上面级液氧贮箱内自由界面变形的3 种典型形式，对后续上面级的推进剂管理技术方案制定及试验验证工作具有参考价值。