列车运行能耗与乘客换乘时间协同优化研究
2020-10-30赵凯丽范贤徐小明朱冬冬
赵凯丽,范贤,徐小明,朱冬冬
(1.合肥工业大学 汽车与交通工程学院,安徽 合肥 230009;2.合肥市轨道交通集团有限公司运营分公司,安徽 合肥 230001)
近年来,城市轨道交通以其准时高效、绿色环保等优点受到居民青睐,逐渐成为城市公共交通的重要组成部分。相比于其他公共交通系统,轨道交通系统的单位运量所需能耗低,但是整个轨道交通系统的运营能耗绝对值高。轨道交通的运营能耗主要分为列车运行能耗和车站运营能耗。车站运营能耗主要是车站设备的能耗,通常为既定的能耗。而列车运行能耗的影响因素较多,据测算,占据城市轨道交通系统总能耗的一半左右[1],降低列车运行能耗对减少轨道交通系统运营能耗具有重要意义。
如何有效降低列车运行能耗是一个较为复杂的优化问题,相关研究大体上可划分为时刻表优化和列车速度曲线优化。时刻表优化主要是通过调整列车发车间隔、停留时间、运行时间等参数降低列车运行能耗。Chen等[2]通过调整列车的停留时间,降低牵引高峰功率值,避免多列车同时牵引的情况,使牵引负荷曲线更平滑。Xu等[3]、Gao等[4]提出一种双目标时刻表优化模型,降低单条线路上的列车运行能耗并减少乘客出行时间。速度曲线优化是通过优化列车的行驶策略,得出列车运行的最优速度曲线。Ichikawa[5]最早利用庞特里亚金原理对列车在区间运行时的节能速度曲线进行了研究。Asnis等[6]通过极大值原理证明了列车在区间运行时的最优速度曲线,包括最大加速、巡航、惰行和最大制动4个阶段。Howlett[7]从不同角度对列车节能运行进行了大量研究,提出求解各阶段转换点的非线性优化方法,为后续的列车速度曲线优化奠定了基础。马超云等[8]通过在给定运行时间的前提下,选择合适的惰行点,实现列车的节能运行。Lu等[9]考虑在满足牵引速度特性、限速等约束下,找出速度转换点,得出节能速度曲线。
部分研究人员考虑再生制动,这是一种能量回收机制,将列车制动时的动能转化为电能,并加以回收利用。基于再生制动,Yang等[10]通过决策列车的停留时间,提高同一供电区间内再生能量的利用率,降低列车牵引能耗。Zhao等[11]以列车的停留时间和车头时距为决策变量,协同相邻列车的牵引、制动时间,最大化再生能量的利用。
在换乘的过程中,乘客需消耗额外的出行时间即换乘时间,换乘时间的长短是衡量轨道交通服务水平的一个重要指标。钱堃等[12]提出城市轨道交通换乘是指在不离开车站付费区及不另行购票的情况下,乘客在不同线路间改变乘坐列车车次的行为。Wong等[13]通过调整列车的到站时间、离站时间、运行时间以及停留时间优化列车时刻表,最小化乘客的换乘等待时间。Wu等[14]基于均衡性的考虑,调整列车在首站的发车时间、运行时间、停留时间以及车头时距,最小化线网中最大的换乘等待时间。Guo等[15]考虑高峰时段和非高峰时段的过渡期内乘客的换乘效率,通过调整列车的到站时间、离站时间、区间运行时间、停留时间和车头时距,协同列车在换乘站的到、发时间,减少乘客的换乘时间。
以上研究通过不同角度和方法对列车运行能耗和乘客换乘时间进行了优化,但忽略了二者的相互影响。考虑到列车时刻表可以直接影响列车运行能耗与乘客换乘时间,本文提出列车运行能耗和乘客换乘时间协同优化模型,通过决策列车的在站停留时间,协调同一供电区间内所有列车之间再生能量的匹配,提高再生能量的利用率,降低轨道交通系统总能耗。同时,通过对停留时间的调整,改变列车在换乘站的到、发时刻,提高换乘线路之间的衔接效率,从而减少乘客的换乘时间。如何平衡城市轨道交通系统运营成本与服务水平,是轨道交通运营公司面临的重要课题。本文通过对列车时刻的优化达到节能高效地运营列车的目的,可为轨道交通运营公司列车时刻表的编制提供参考。
1 问题描述
地铁的制动系统包括电制动和机械制动,电制动是列车通常采取的一种制动方式,分为电阻制动和再生制动。电阻制动是指列车的牵引电机处在发电工况时,将列车制动时的动能转化为电能,再通过电阻将其以热能的形式消耗。该制动方式会导致隧道温度上升,增加空调及通风系统的用电量,造成资源浪费。不同于电阻制动,再生制动是将列车制动时转化的电能反馈到接触网中回收再利用,可有效节约电能。城市轨道交通一般站间距短,列车加速、制动操作频繁,故再生制动是比较理想的制动方式。本文基于再生制动增加同一供电区间加速、制动列车的重叠时间,使再生能量能够及时被同一供电区间内的正在加速的列车使用,从而减少牵引列车从变电所消耗电能。
随着城市轨道交通的大规模建设和人们的出行需求不断增加,网络化运营成为城市轨道交通发展的必然趋势。人们为了完成一次出行,通常需要综合使用多条线路,形成了轨道交通换乘。换乘时间主要包括乘客通过换乘通道的走行时间和换乘等待时间,而走行时间往往取决于乘客自身和换乘站的布局形式,在优化上具有一定的局限性,故换乘时间的优化主要是减少换乘等待时间。本文通过优化列车时刻表协调列车在换乘站的到、发时刻,提高各线路在换乘站的衔接效率,实现乘客换乘时间最小化。
由于轨道交通线路通常被分为多个供电区间,在本研究中,所有单向列车均由该区间所在的变电站供电,在同一方向上,线路上所有列车在每一个供电区间的运行模式相同。
2 优化模型
为建模和求解方便,本文做出如下假设:
(1)乘客在每个车站的到达率和换乘到其他线路的换乘率是已知的;
(2)列车的容量足够大,当列车到达换乘站时,可以容纳站台上所有需要换乘的乘客,不存在乘客等待下一趟列车的情况;
(3)同一列车在不同循环中的停站时间和区间行驶策略相同,为了计算方便,我们假设同一列车在不同循环中的同一车站和同一区间的停站时间和驾驶策略相同且固定;
(4)反馈到电网中的再生能量能够立即被同一供电区的加速列车所使用,若反馈的再生能量没能被及时吸收,则被接触网中的电阻所消耗。
线路r示意图见图1。
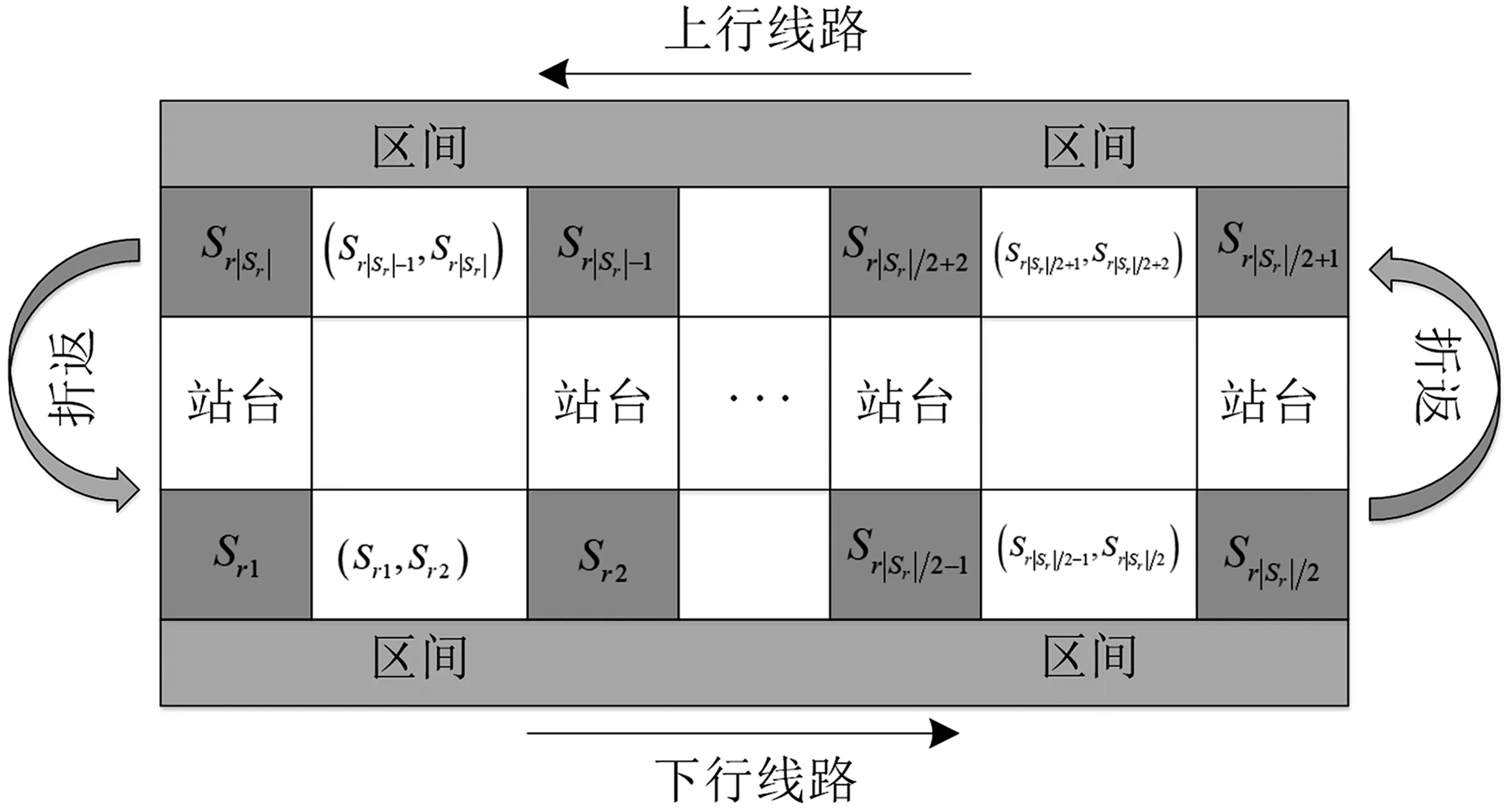
图1 线路r示意图Fig.1 Schematic of line r
2.1 参数
表1列出了本文所用的输入参数。

表1 输入参数Table 1 Input parameters

续表1
2.2 变量
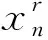
(1)
(2)
(3)
2.3 目标函数
2.3.1 列车运行能耗
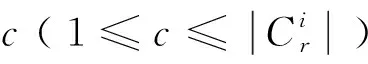
(4)
式中,(c-1)·Tr为列车i执行c循环之前的(c-1)个循环所需的运行时间,(i-1)·hr为列车i与第一列列车之间的车头时距。
记N=|Sr|/2,则第i列车离开r下行线路车站n(n∈{sr2,sr3,…,sr(N-1)})的时刻为:
(5)
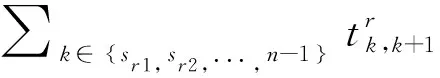
同理,第i列车在其第c个循环中离开r上行线路首站n(n=sr(N+1))的时刻为:
(6)
第i列车在其第c个循环中离开r上行线路车站n(n∈{sr(N+2),sr(N+3),...,sr2(N-1)})的时刻为:
(7)
根据(n,n+1)区间的实际速度曲线,第i列车在其第c个循环中,列车在该区间内t时刻的速度为:
(8)
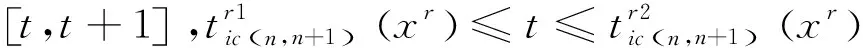
(9)
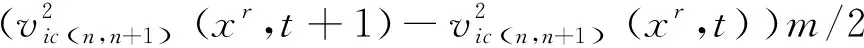
若列车在区间运行时行驶策略不变,则区间运行能耗是一个常数。第i列车在其第c个循环的区间(n,n+1)运行时所需能耗为:
(10)
整个系统所需电能总量为:
(11)
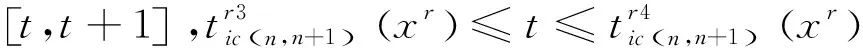
(12)
如前所述,供电区间内制动列车产生的再生能量可被同一供电区间的牵引列车使用。因此,任意[t,t+1]时间段内供电区间u∈U内再生能量利用量为:
(13)
记解为x时,整个系统运营期间内的再生能量总利用量为:
E′(x)=∑u∈U∑1≤t≤TE′(u,x,t) ,
(14)
则系统所需的总运行能耗为E(x)=E-E′(x)。
2.3.2 换乘等待时间
本文基于先到先服务(first in first out,FIFO)规则[16],分析乘客换乘情况。由假设(1)得,当列车到达换乘车站时,车上需要下车换乘至其他线路的乘客数量是已知的。由假设(2)得,不存在乘客需要等待下一趟列车的情况。
由于一条线路包括下行和上行方向,故2条可换乘线路之间存在8种换乘场景。当乘客从线路r换乘到r′时,将会有4种场景,分别是乘客从r下行线路上的列车换乘到r′下行线路上的列车和r′上行线路上的列车,以及从r上行线路上的列车换乘到r′下行线路上的列车和r′上行线路上的列车。
(15)
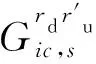
(16)
当乘客从r下行线路上列车i的第c个循环换乘到r′下行线路上列车i′的第c′个循环时,换乘时间为图2中A1,A2,A3的总面积,记乘客从r下行线路上列车i的第c个循环换乘到r′下行线路上列车i′的第c′个循环的换乘时间为S1:
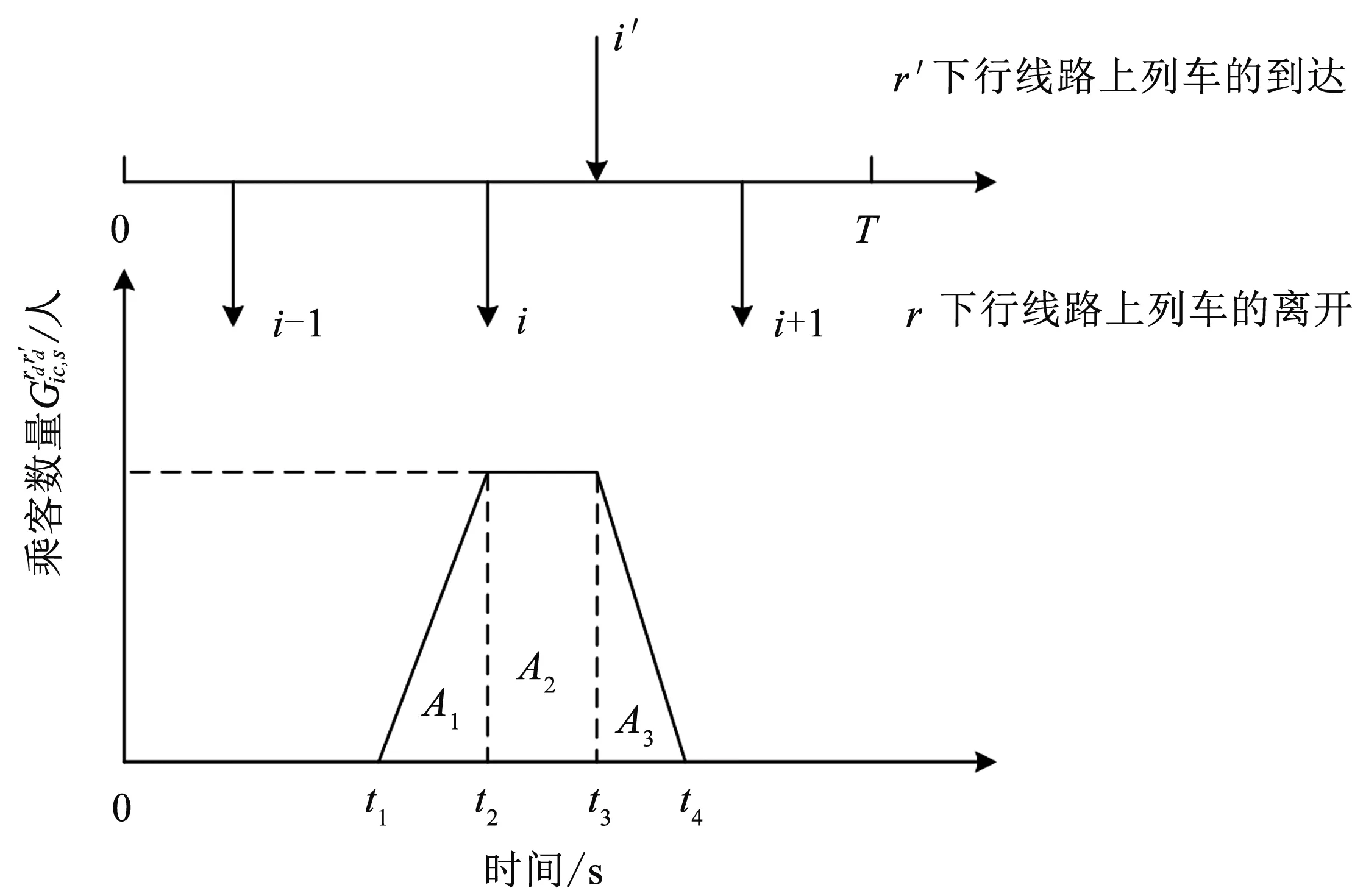
图2 换乘站内换乘乘客随时间变化的示意图Fig.2 Change in transfer of passengers over time at the transfer station
(17)
式中,t1和t2分别为r下行线路上列车i在其第c个循环到达和离开换乘站的时刻,t3和t4分别为r′下行线路上列车i′在其第c′个循环到达和离开换乘站的时刻。
类似地,可计算出乘客从r下行线路列车i的第c个循环换乘到r′上行线路列车i′的第c′个循环的换乘时间S2,以及从r上行线路列车i的第c个循环换乘到r′下行线路列车i′的第c′个循环的换乘时间S3和换乘到r′上行线路列车i′的第c′个循环的换乘时间S4。
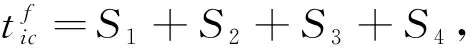
(18)
则系统总换乘时间为:
W(x)=∑r∈R∑r′∈R,r≠r′Wrr′(x) 。
(19)
2.4 优化模型
由于运行能耗和换乘时间的单位和量纲具有差异性,此处对每一个目标函数进行归一化处理如下:
(20)

本文采用线性加权和法将双目标优化模型转化为单目标优化模型,模型如下:
(21)
(22)
(23)
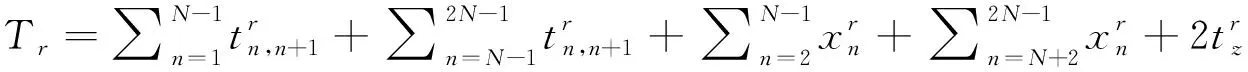
(24)
(25)
(26)
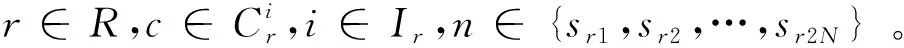
3 求解算法
遗传算法是基于自然界进化规律演化而来的随机搜索方法,可有效地解决最优化问题,广泛应用于交通运输领域[3,10]。本文采用遗传算法,对上述列车运行能耗和乘客换乘时间协同优化模型进行求解。
3.1 初始化种群
为了提高算法的执行效率,本文在算法设计上采用实数编码方式,染色体上的基因由各条线路及线路上各站的停留时间组成,如图3所示,l为线路集合R中的线路数量。在当前时刻表的在站停留时间基础上调整变化范围,生成初始解。为保证总停留时间不变,在生成初始解时,一条染色体上的其他基因在其范围内随机产生,最后一个基因大小为总基因之和与其他站点的基因和之差。这种初始解的生成方式,可能导致列车在最后一个车站的停留时间超出允许的范围,此时的解是不可行解。我们在生成初始种群时直接将不可行的解舍弃,保证初始种群中的染色体都是可行解。
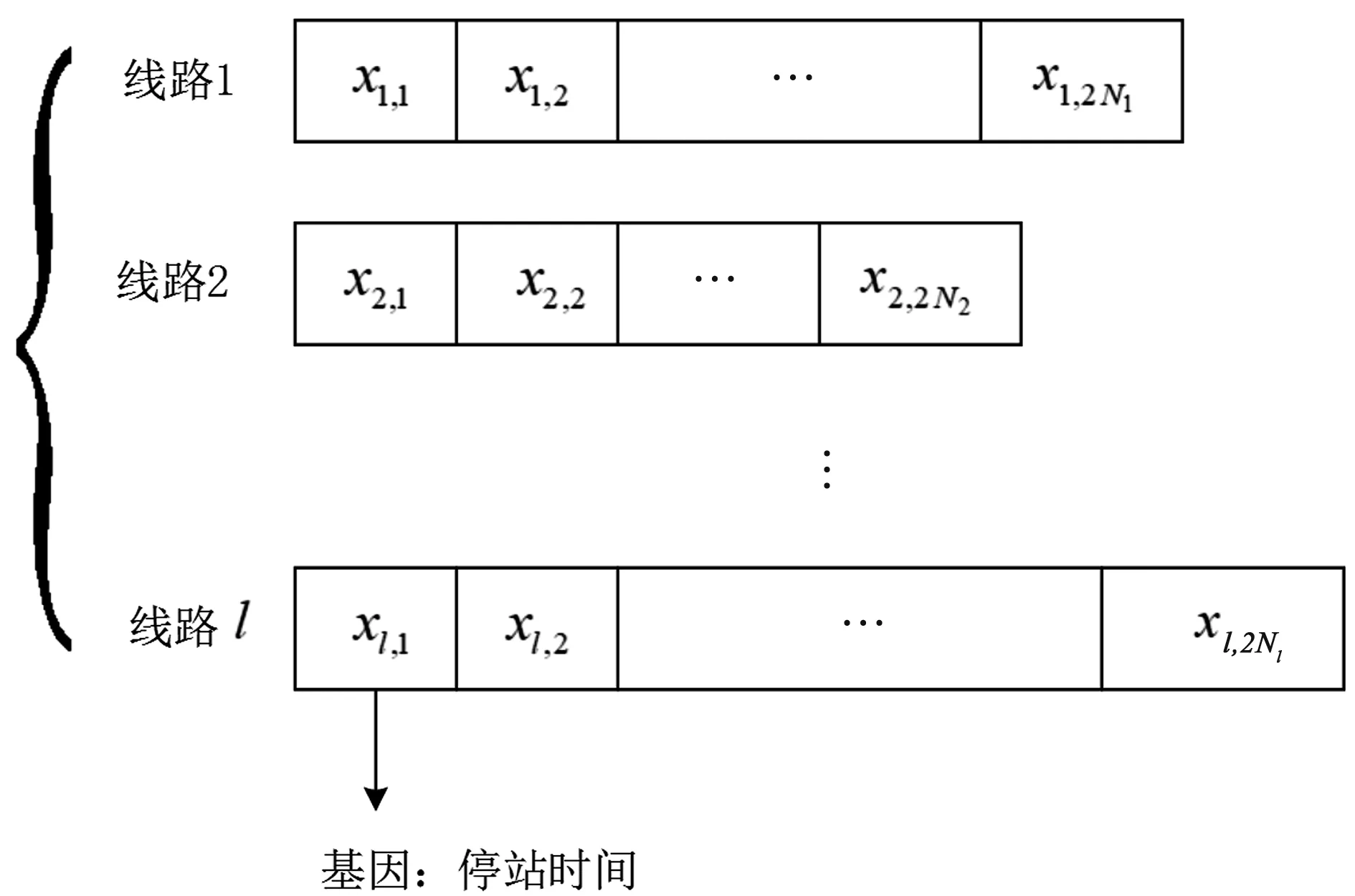
图3 染色体示意图Fig.3 Diagram of the chromosome
3.2 选择
选择操作是一种优胜劣汰的过程。应用评估函数(21)计算上一代种群中每个染色体的适应度,并采用轮盘赌方法选择适应度高的染色体。
3.3 交叉
交叉操作是进行染色体之间的信息交换、更新解的过程。由于采用的是实数编码,对于上一步选出的新种群,采用顺序交叉法,将相邻染色体进行两两交叉。产生随机数r,交叉概率为Pc,当r≤Pc时,将相邻染色体之间进行线性组合交叉操作,交换信息,得到新的子代染色体。值得注意的是,如果父代的染色体是可行解,那么采用这种交叉方式得到的新的染色体必定是可行的解。
3.4 变异
对于交叉后产生的新种群,通过变异操作进一步更新解。产生随机数r,变异概率为Pm,当r≤Pm时,该条染色体进行变异操作,为了保证列车在车站的总的停留时间不变,随机选取3组,每组2个,共6个变异基因点进行变异操作。每一组基因中的一个基因在其停留时间上下限范围内进行变异,而另一个基因用于调整,以保证总停留时间不变,由此产生新的个体。但这种变异方式可能造成用于调整的基因超出停留时间允许的范围,此时,我们重新选择变异的基因点进行变异操作,直到变异后的染色体对应于一个可行解。
4 算例
本节以北京地铁亦庄线和5号线为例展开算例研究。亦庄线有14个车站,6个变电站,如图4所示;5号线有23个车站,12个变电站,如图5所示。宋家庄站为两条线路之间唯一的换乘站。
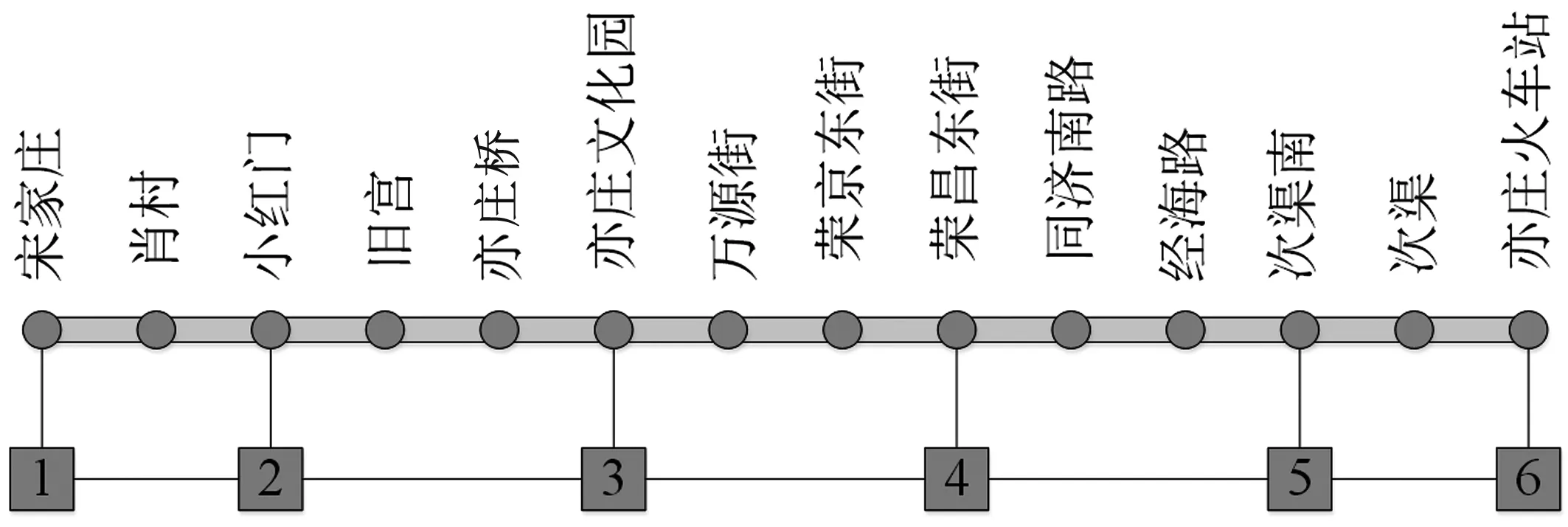
图4 北京地铁亦庄线示意图Fig.4 Map of the Yizhuang Line of Beijing metro
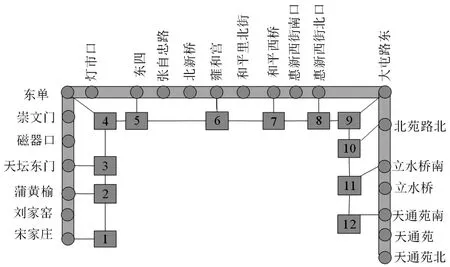
图5 北京地铁5号线示意图Fig.5 Map of Beijing metro Line 5
给定列车时刻表规划时间段长度T=3c,c=4572,种群大小为200,最大迭代次数为100代,列车的在站停留时间变化区间为[-10,10],其他参数见表2。

表2 参数设置Table 2 Parameters used in case studies
当前亦庄线运营数据见表3,且基于本文模型计算得出系统总能耗为28 682.46 kW·h,总乘客换乘时间为9 083.37 h。在算例中,当权重设置为σ1=0.5,σ2=0.5时,得出优化后的时刻表,如表4所示。为了更直观地反映模型的有效性,本文分别列出了3组不同权重组合的优化结果,并与当前时刻表对应的结果相比较,如表5所示。当σ1=0.5,σ2=0.5时优化后的系统总能耗为27 204.10 kW·h,总换乘时间为7 479.45 h,较优化前,系统总能耗降低了5.15%,总换乘时间降低了17.66%。当σ1=1,σ2=0时,优化的系统总能耗为26 901.19 kW·h,总乘客换乘时间为9 169.73 h,较优化前,总能耗降低了6.21%,而此时总换乘时间较优化前增加了0.95%。当σ1=0,σ2=1时,优化后的地铁系统总能耗为27 854.68 kW·h,总乘客换乘时间为7 339.48 h,较优化前,总能耗降低了2.89%,总换乘时间降低了19.20%。
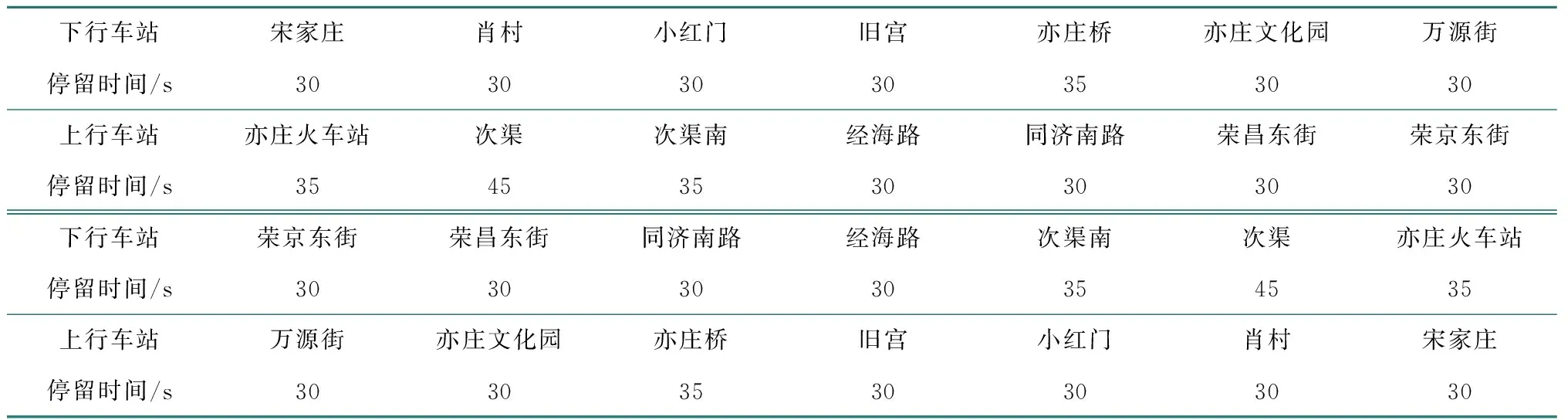
表3 亦庄线当前时刻表的在站停留时间Table 3 The dwell time on the current timetable of Yizhuang Line
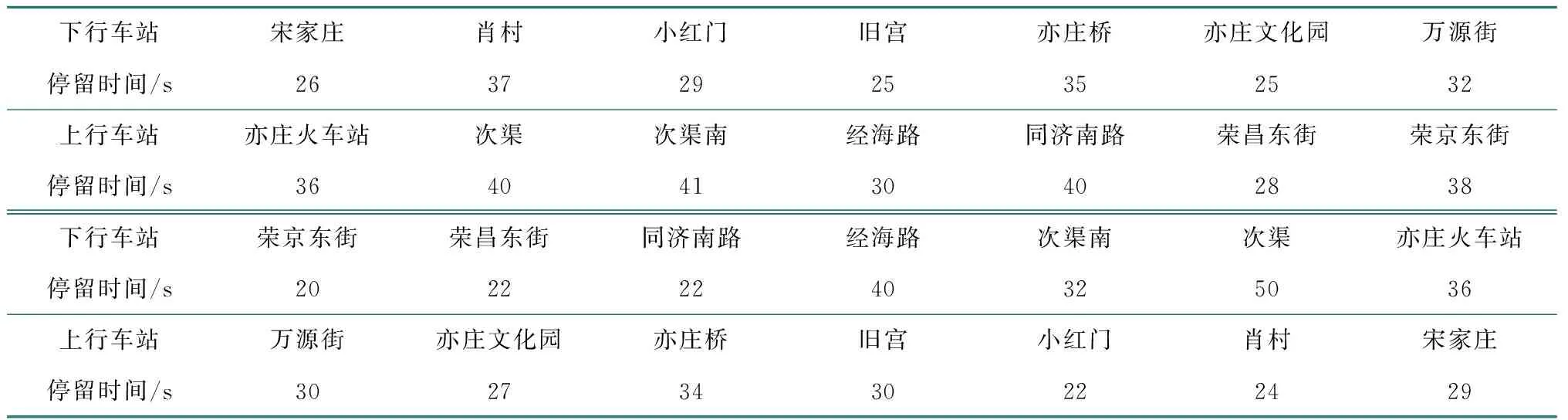
表4 优化后的列车在站停留时间Table 4 Optimized train dwell time at stations

表5 不同时刻表的列车运行能耗和乘客换乘时间的值Table 5 The values of train energy consumption and passenger transfer time in different timetables
表6列出了4组不同权重组合下得到的目标函数值。可以看出,系统总能耗的归一化目标值随着其权重的增加而减小,即再生能源的利用量随着其权重的增加而提高,从而系统能耗逐渐减少。乘客换乘时间的归一化目标值随着其权重的减小而增大,即乘客换乘时间逐渐增大。实际应用中,可依据具体需要,调整两个目标的权重大小得到理想的优化结果。
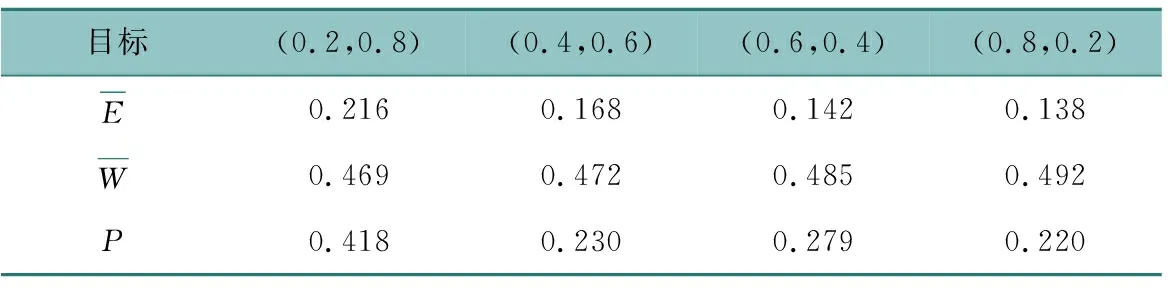
表6 不同的权重组合下的目标函数值Table 6 Objective function values with different weight combinations
5 结论
本文首先提出了列车运行能耗和乘客换乘时间协同优化模型,旨在降低轨道交通系统总能耗及减少乘客的换乘时间,然后采用遗传算法对模型进行求解,最后结合北京亦庄线和5号线运营数据开展了算例研究。实验结果显示,当设置权重为σ1=0.5,σ2=0.5时,得出优化后的时刻表,与当前时刻表相比,轨道交通系统总能耗减少5.15%,乘客换乘时间降低17.66%,验证了模型和算法的有效性。需要说明的是,本文将乘客的到达率和换乘率等参数均假设为给定常数,而实际中这些参数是随机的,这也是下一步工作中将考虑改进的问题。
