基于中央空调的几种负荷预测方法对比分析
2020-10-30郭虹李壮举
郭虹 李壮举
北京建筑大学电气与信息工程学院
中央空调作为公共建筑中重要的基础设施和主要耗能设备,必须要采用合理的运行调节方法来提高能源利用效率。而空调负荷预测作为优化空调运行的基础,也是蓄冷空调系统高效经济运行的关键所在。随着负荷预测方法不断的进步与发展,现如今已经存在众多不同种类的空调负荷预测方法。而在实际应用中,各个预测方法通常会因为自身的局限性和适用条件而无法满足当前工程。因此,为了满足空调负荷预测的工程实用性,本文拟对几类典型的空调负荷预测方法进行基于实际工程下的分析对比[1-3]。由于预测方法门类较多,拟从不同类别的预测方法中选取具有典型性的线性回归(Line Regression)、非线性回归(Non-linear Regression)、指数平滑(Exponential Weighted Moving Average)、灰色预测(Grey Prediction)和人工神经网络(Artificial Neural Network)这五种方法进行中央空调冷负荷预测的研究[4-5],并选取预测精度、响应速度此类负荷预测中常用的对比指标[6],及建模的复杂程度,对输入数据的要求以及模型的适用性等三个新的切入点,通过建模仿真,多角度全面的分析比较以上五种典型预测方法各自的特点与实用性,以期得到在实际工程应用中有指导意义的空调系统负荷预测方法。
1 负荷预测的基本问题
1.1 影响负荷的主要因素
中央空调系统的冷负荷是一个典型的具有慢时变性、多干扰性、不确定性等随机特性的非线性模型。用预测模型进行空调冷负荷的预测,主要是依靠影响空调冷负荷的各种干扰因素,对未来某一时刻或某段时间内的空调冷负荷做出预测[7-8]。
研究表明,室外气象因素对空调冷负荷的干扰程度从大到小的顺序依次为:室外干球温度、室外太阳辐射、室外相对湿度、室外风速、天气状况、星期几。因此在本次实验中,选取室外干球温度、湿度、总辐射三个室外干扰因素作为干扰输入[9-10],并结合数睿思竞赛平台提供的某建筑物6 月1 日-9 月30 日的逐时空调日负荷及气象数据,共计2928 组实验数据作为研究对象,用内存为4.00 GB、64 位操作系统的Win10 系统作为实验用的计算机,以MATLAB2016 作为实验平台进行数据处理,建模以及预测。将前2905 组数据作为学习对象进行建模,并输出最后一天即9 月30 日的预测负荷与实际负荷的对比数据进行预测方法的特性分析。
1.2 预测精度评价指标
不同的考核指标可以反映负荷预测的不同侧重点。本文预测的是建筑物的短期冷负荷,因而采用概率统计分析的方法,考察具体的日负荷预测准确率及日合格点百分数。其中,日负荷准确率侧重于对负荷预测误差整体性的刻画。日合格点百分数侧重于对单点负荷预测误差的考察[11-12]。
日负荷预测准确率的计算方法如下:

式中:Ak为日负荷预测准确率;LFi,LRi分别为负荷的预测值和实际值;n 为日负荷预测总点数(24 点);Ei为单点负荷的相对预测误差;i=1,2,…,24。
对于单点负荷来说,相对预测误差Ei≤3%时,该点为合格点。
日合格点百分数的计算方法如式(3)所示:

式中:N1为日24 点预测负荷中合格点的个数;Ri≥97%的预测日为合格日。
2 数理统计预测法
负荷预测准确度与建筑负荷的数学模型有着直接的联系。随着建模和仿真技术的不断发展,负荷预测的方法取得了巨大进步。随着理论研究的逐步深入,负荷预测的方法也在不断地改进,本文首先介绍四种典型的基于数理统计的预测方法,分析在研究对象不变的情况下,不同的预测方法各自的特性。
2.1 多元线性回归
线性回归法通过回归分析来确定输入变量和输出变量间的关系,是一种基于数理统计分析的方法[13],而线性就是指输入变量和输出变量之间的关系是由直线构成[14-15]。其表达形式为y=βixi+e。
本次实验中,选取了三个对空调冷负荷有影响的主要因素,即回归模型中存在三个输入量,分别是干球温度,辐射强度和湿度[16-17]。依次用x1,x2,x3表示输入变量,β1,β2,β3,β3表示输入的参数,y 为输出变量即空调负荷。得到如式(4)所示的线性数学关系,并用于MATLAB 仿真得到图1 所示的曲线图。
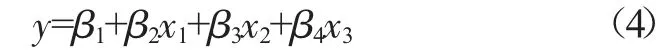

图1 被测建筑9 月30 日冷负荷线性回归预测值-实际值对比图
经仿真得到多元线性回归的参数值,β1=-7941.88,β2=316.20,β3=25.42,β4=3.17。将预测值与实际值在Excel 中进行对比,计算相对误差Ei,并代入式(1),(3)中,计算得到日负荷预测准确率A1=-1274.9%,日合格点百分数R1=0.0%。
2.2 多元非线性回归
如果回归模型的输出变量是输入变量的一次及以上的函数形式,则回归模型在图形上表现为曲线形式,这类模型称为非线性回归型[18-19]。与线性回归模型类似,非线性回归模型由于输入变量的个数,也分为一元和多元两种类型[20-21]。
本次实验中采用如式(5)所示的多元非线性的三次项函数进行建模,代入输入、输出量,在MATLAB中进行仿真,得到如图2 所示的比较曲线。


图2 被测建筑9 月30 日冷负荷非线性回归预测值-实际值对比图
经仿真得到了多元非线性线性回归的参数值,β1=0.14,β2=-0.05,β3=1.99。将预测值与实际值在Excel中进行对比,计算相对误差Ei,并代入式(1),(3)中,计算得到日负荷预测准确率A2=-164.9%,日合格点百分数R2=0.0%。
2.3 指数平滑
指数平滑预测是通过利用原始的负荷数据,无需额外的影响因素作为输入。在原始数据中引入一个加权因子(即平滑系数),以求得预测数据的一种方法,属于时间序列预测范畴[22-23]。指数平滑预测法的基本思想是,预测值是历史数据的加权和,且对不同的历史数据给予不同的权数,新数据给予较大的权数,旧数据给予较小的权数[24]。
在本次实验中,为了使预测的结果更为准确,选用三次指数平滑法进行预测,它的原理式如下:
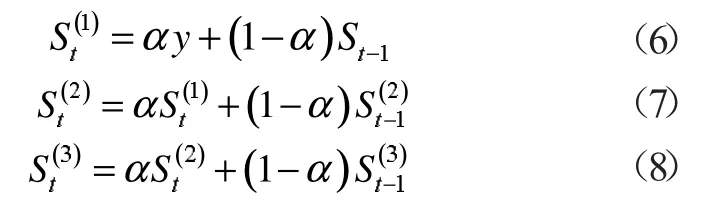
依据经验,当原始数据为平稳序列时,参数α 的取值范围为0.1~0.3,而数据波动较大时,参数α 的取值范围为0.6-0.9。因此实验中,选取参数α 的值为0.9,得到如图3 所示的比较曲线。通过计算得到日负荷预测准确率A3=50.7%,日合格点百分数R3=12.5%。
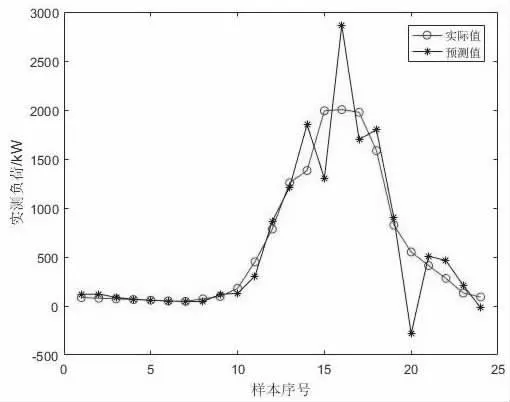
图3 被测建筑9 月30 日冷负荷指数平滑预测值-实际值对比图
2.4 灰色预测
灰色预测是通过把分散在时间轴上的离散数据看成一组连续变化的序列,通过对这组数据的累加和累减,将灰色系统中的未知信息弱化,把已知因素的影响程度强化,构建一个以时间为变量的连续微分方程,通过数学方法确定灰色预测的参数,从而实现预测目的。它具有所需数据样本少、短期预测效果好、运算过程简单等优势[25-26]。
对灰色系统进行预测的模型称为灰色模型(Grey Model,简称GM 模型),一般的表达方式为GM(n,x)模型,其具体含义是:用n 阶微分方程对x 个变量建立模型[27-28]。
本次实验中采用的是GM(1,4)模型,即用1 阶微分方程对4 个变量建立模型。并得到对比数据(图4),计算得到日负荷预测准确率A4=1.6%,日合格点百分数R4=0.0%。

图4 被测建筑9 月30 日冷负荷灰色预测值-实际值对比图
3 BP 神经网络
BP(Back Propagation)神经网络是1986 年由Rumelhart 和McClelland 为首的科学家提出的概念,是一种按照误差逆向传播算法训练的多层前馈神经网络,适用于语言、模式识别、自适应控制、负荷预测等,是目前应用最广泛的神经网络[29]。因此,本文选用BP 神经网络对空调冷负荷进行预测。
本次实验中,选取实验数据的前2905 组数据作为训练集进行训练,用最后24 组数据作为测试样本进行预测,实验选用三层前馈网络,确定输入层变量分别为:实际负荷值,干球温度,辐射强度和湿度四种,即输入层神经元个数为n=4;输出层神经元个数m=1;取a=10,则得到隐含层神经元个数。
在输入实验数据前,首先应对数据进行归一化处理,以实现数据指标之间的可比性。神经网络的归一化处理,一般变量的取值在[-1,0]、[-1,1]或[0,1]之间,这样做是为了弱化某些变量的值较大而对模型产生影响。在本次实验中,将变量的取值收敛于[0,1]之间,以便于剔除误差较大的数据,得到更准确的实验结果。在对数据进行归一化处理后,开始构建神经网络,创建一个输入层节点为4,隐含层节点为12,输出节点为1 的BP 神经网络。设置最大迭代步数为1000,设置学习速率为0.05,%设置学习目标为0.000000001,如图5 所示。然后输入数据开始学习。

图5 神经网络结构图
根据计算(图6)得到日负荷预测准确率A5=99.96%,日合格点百分数R5=100%。

图6 被测建筑9 月30 日冷负荷神经网络预测值-实际值对比图
4 结语
本次实验是根据某建筑6 月30 日-9 月29 日的历史气象数据与空调冷负荷数据进行建模和学习,并预测输出9 月30 日全天的空调冷负荷数据,属于短期负荷预测。在MATLAB 中进行仿真之后,得到了不同的预测方法输出的预测结果,在表6 中进行统一比较,并分析说明每种方法的特点。
1)线性回归预测法的精度很低,这是因为空调的负荷模型不是线性模型导致,由于线性回归模型是以线性关系去连接相邻两个预测点,因此在建模过程中容易出现误差较大的点,且响应速度较慢,所以对于呈非线性关系的负荷预测模型和中长期负荷预测,线性回归预测的响应速度会越来越长,且单点的误差越来越大。
2)非线性回归预测法的精度也较低,虽然非线性模型是以曲线连接负荷预测的相邻点,然而非线性回归模型的学习能力较差,因为天气因素影响的空调负荷变化较前一天差异较大时,容易出现模型不适用的情况。所以对于负荷变化波动较大的负荷模型,非线性回归预测也存在较大的误差,但是相较于线性回归预测,非线性预测的响应速度和精度都有所提高。
3)对比前两种预测方法,指数平滑法显然拥有更高的精度及响应速度很快,指数平滑考虑了预测日附近的负荷的权重,考虑了近期的负荷趋势,因此这种预测方法可以更加合理的反应负荷的变化趋势。且每进行一次平滑,它的预测结果准确率就会更高,综合考虑它的预测精度和响应速度,这种方法适用于精度较低中长期负荷预测。对于灰色预测来说,它的建模十分容易,且仅需要历史负荷数据就可以进行建模,所以运算迅速,响应很快,但与线性回归预测类似,灰色预测也适用于线性短期负荷预测。
4)BP 神经网络是预测精度最高的预测方法,但同时,由于它的建模过程复杂也延长了它的响应速度,因此对于短期和中期负荷预测来说,它的预测精度很高,且响应速度也在一般工程应用的承受范围内。由此可见,神经网络在实际应用中的占比也很大。

表6 预测方法对比表
选择合适的预测方法进行负荷预测在实际工程中有很重要的意义,在实际应用中,要综合考虑实际空调负荷的时间长短,精度要求,响应速度,数据需求和建模难易程度去选择适合实际工程的负荷预测方法,以达到最佳的预测效果。本文根据实验结果及分析得出结论:神经网络方法的响应速度较慢但具有较高预测精度,适用于精度要求较高的短期负荷预测。而季节性指数平滑法的响应速度较快且精度较高,也具有较好的工程应用价值。
