基于时差处理的自适应多层次软测量建模方法*

邱禹 马兴灶 吴菁

学术研究

基于时差处理的自适应多层次软测量建模方法*

邱禹1马兴灶1吴菁2

（1.岭南师范学院机电工程学院，广东 湛江 524048 2.华南理工大学自动化科学与工程学院，广东 广州 510640）

在污水处理过程控制中，软测量是针对难以测量变量进行有效测量的一种手段。然而，建模输入的使用限制，使一些与预测目标相关但不易获取的变量不宜作为输入信息，阻碍了建模。对此，提出一种多层次软测量建模方法。首先，利用支持向量回归建立多个软测量子模型，输出与最终目标变量相关但不易获取的子目标；然后，利用预测的子目标与原始辅助变量构造主模型的输入变量集，增加预测所需的输入信息，从而提高预测效果；同时，在建模中引入一种时差处理方法，增强模型的自适应能力，应对因外部干扰而导致的性能退化问题；最后，通过仿真案例对本文所提方法的有效性进行验证。结果表明：本文所提方法相对于单模型SVR（缺少CODe信息）和单模型SVR（具有完整CODe信息），有更好的预测表现，为0.0398，为0.9987。

污水处理；软测量；建模；多层次；自适应

0 引言

在污水处理过程中，为确保过程控制系统的有效运行和出水水质的稳定，需监测诸多过程变量。然而，一些变量，如生化需氧量（biochemical oxygen demand, BOD）等，因内在属性及经济成本的原因存在实时测量困难的问题。对此，软测量技术提供一种可行的解决方案[1-4]。

数据驱动软测量技术基于系统的过程历史数据，其核心在于建模。常用的建模方法有：线性的主元分析（principal component analysis, PCA）[5]、偏最小二乘（partial least square, PLS）[6-8]等；非线性的神经网络[9-10]、支持向量机[11]等。建模方法的考虑在于建立合理的软测量系统以满足需求。其中，一个常被忽略的问题是建模出发点的偏离。软测量要根据对象的实际情况，基于可测或易测变量的历史数据建模。然而，输入信息的使用局限，增加了建模难度。

输入信息对数据模型非常重要。一些关键信息的缺失会导致模型预测精度下降或模型结构复杂化[12]。因此，部分研究在某些场景下不考虑实际应用的限制，而采用与目标相关但不易测的变量作为输入。如文献[13]在预测SVI时，采用混合液挥发性悬浮固体浓度（mixed liquid volatile suspended solids, MLVSS）作为输入，并在实验室550℃工况下每周测定，而不是在线实时获取该变量；文献[14]在预测BOD浓度时，虽然引入了一种基于互信息的特征选取方法，从22个候选变量中选取10个作为模型输入，但仍包含同为难测变量的进水BOD浓度。以上例子都将同属于不易测范畴的变量纳为输入信息来建立模型，这与软测量技术的初衷相违背。因此，如何在满足精度需求的同时，合理解决输入端缺失的重要输入信息，是软测量技术应用容易忽略且有待研究的问题。多模型策略提供了一种可行的解决思路。

传统多模型软测量建模方法主要有加权组合和模型切换。加权组合方法是针对非线性系统的每个子系统设计相应的局部模型，再通过一种线性或非线性的关系构成对应母系统的全局模型[15-16]。模型切换方法通过一个基于某种性能指标的切换函数，在每次预测前，选择使性能指标最小的元素模型进行输出[17-18]，保证了预测精度。

加权组合和模型切换建模方法主要针对多工况复杂非线性系统的建模或控制问题，利用多模型更好地逼近系统的动态性能，但无法解决建模输入限制问题，即如何处理重要但不易获取的输入变量用于建模。针对该问题，本文提出一种多层次建模方法——自适应多层次软测量建模。模型框架主要由主模型（primary model）和二次模型（secondary model，也称辅助模型）2部分构成。辅助模型基于并联形式串联到主模型，输出主模型输入中缺少的重要信息，构成一种系统软测量模型。支持向量机回归（support vector regression, SVR）是一种非线性建模方法，已被证实在软测量应用中是有效的[19-21]。本文采用SVR建模方法建立主次模型。同时，在系统建模中引入一种时差（time difference, TD）处理方法，用于应对外部干扰，如传感器漂移、外界环境变化（天气、季节）等导致的性能退化问题[22-23]，增强模型自适应能力。

1 时差建模方法

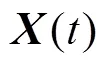
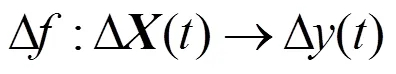
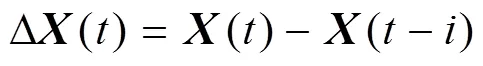
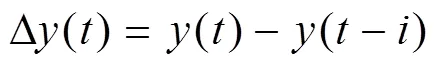
时差处理能够消除外部干扰的影响，使变量内在分布规律平稳，从而提升建模效果[12]，其流程如图1所示。时差建模方法有助于维持稳定的预测精度[24-25]，避免了相关问题[26]。

图1 时差建模流程

2 支持向量回归

支持向量回归是基于支持向量机（support vector machine, SVM）的一种回归方法，通过应用核技巧（kernel trick）将SVM用于处理非线性回归问题。本质上，SVR是一种优化问题，其主要形式为

通过求解式(5)，可构建一种具有平衡泛化能力和过拟合的回归模型：

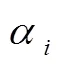
通过式(6)可以看出：SVR的核心在于核函数，不同的核函数将形成不同算法。实质上，通过核函数的非线性映射可将输入空间映射到一个高维特征空间，然后在这个空间中进行线性回归，从而取得原空间非线性回归的效果。其中研究和应用最多的核函数是高斯核函数：

3 自适应多层次软测量建模的实现

本文提出一种自适应多层次软测量建模方法，其框架如图2所示。

图2 自适应多层次软测量建模方法框架

多层次建模方法主要是为了解决输入信息贫乏问题。影响模型预测能力的主要因素有模型解析能力和输入信息，其中输入信息更为重要。当输入与输出之间的相关性较弱时，建模难度增大。因为仅靠输入信息已不足以对输出变量进行准确预测，因此需要模型能够对预测误差进行补偿。误差越大，模型需要补偿的信息就越多，模型也越复杂。而多层次建模方法能够丰富预测目标变量时缺失的重要输入信息，对模型解析能力无过高要求，无需构造复杂的模型结构或训练算法，从而降低了建模难度。

自适应多层次软测量建模流程如图3所示。图3(a)为系统模型的离线建模部分：首先，与预测目标相关的可测变量集的历史过程数据经过时差处理使数据序列平稳化，目的在于将变量的变化趋势包含其中，以便随时间衰减的影响能得到解释；然后，根据与预测目标的相关性程度，选择二次模型和主模型的输入，进行建模。图3(b)为系统模型的在线实施部分。离线部分构建的系统软测量模型作为核心部分用于预测，模型输出需要进行反时差处理以恢复为原数据格式，才能作为最终预测结果。

图3 自适应多层次软测量建模流程

4 案例研究

通过案例验证基于时差处理的自适应多层次软测量建模的有效性。首先，本文所提建模方法虽然可以建立多个辅助模型，但前提是存在多个与最终预测目标相关性高但不易获取的变量；再者，案例研究的主要目的是验证方法的有效性，模型规模不是主要考虑方面。因此，为使验证过程清晰易懂，在本案例中只用到1个辅助模型进行说明。

验证过程从2方面考虑：

1）应用性能，多层次建模考虑了不易测输入变量的信息，为验证本文所提方法比单模型建模具有优势，本文所提方法与单模型SVR（缺少相关输入信息）就单目标预测性能进行对比研究；

2）理论性能，多层次建模方法需建立多个层次模型来构造缺失的输入信息，从而增强预测性能；在不考虑实际应用性，具有完整输入信息的前提下，为验证本文所提方法的性能，本文所提方法与单模型SVR（具有完整输入信息）进行对比研究。

评价指标选用均方根误差（root mean square error, RMSE）和相关性系数。值越小，模型的预测性能越好，其定义为

4.1 基准仿真模型

4.1.1 背景简介

基准仿真模型1（benchmark simulation model 1, BSM1）是由国际水协会（international water association, IWA）提出的一种基准仿真环境，其提供一种无偏差的基准系统，以便比较不同的控制策略而无需参照具体设施，如图4所示。

图4 BSM1定义下的污水处理过程

在BSM1定义的仿真环境中，污水处理过程由5个活性污泥反应池（6000 m3）和1个二沉池（深4 m，10层，6000 m3）构成。其中，活性污泥反应池由2个缺氧池和3个好氧池组成；日平均处理污水量为20000 m3，可生物降解的化学需氧量为300 mg/L；同时涵盖了硝化和前置反硝化过程以实现生物脱氮。1号活性污泥模型（activated sludge model no.1, ASM1）用于描述生化反应池内发生的生化反应。

4.1.2 场景定义

本案例中，选择出水BOD5作为目标变量来验证模型的有效性。BOD是反映水体被有机物污染程度的一种重要综合指标。对于大多数的中小型污水处理厂而言，BOD大多通过人工化验方式确定，即5天培养法测定BOD值，因此称为BOD5。这种测量方式实时性较差，化验结果大大滞后于污水的排放过程，容易造成二次污染。BOD5的实时检测一直是污水处理软测量研究的主要内容。本案例根据工艺机理分析，初步选取与BOD5相关的初始辅助变量，最终通过实地考察选取可（易）测量且经济性高的初始辅助变量作为辅助变量，如表1所示。其中，CODe是出水总化学需氧量，反映水体受还原性物质污染程度的一种综合指标，同时也是一种不易测量变量。基于现实可行性操作，不建议其作为输入用于模型预测。因此，本案例中CODe作为二次模型的预测目标，用于补充主模型的输入信息，而其余变量则同时作为主、次模型的输入。

表1 辅助变量

在雨天场景下，闭环运行BSM1仿真模型2周。设定15 min采样率，共采集1344个样本数据。选择雨天场景是因为恶劣天气条件具有外部干扰等因素，能进一步考验本文所提方法的有效性（泛化性能）。

4.2 测试结果

在测试前，对软测量模型的一些重要参数进行预定义：

1）时差间隔，时差处理需明确时差间隔，本案例将时差间隔设定为变量的采样间隔，即15 min，时差间隔较小时，时差变量虽然可以反映更多的短期变化，但也因此包含更多噪声；反之，时差间隔较大时，无法准确反映过程状态的短期变动信息，因此，通常将采样间隔设为最小可行的时差处理间隔；

2）核函数，选用高斯函数作为SVR模型的核函数，具体参照式(7)；

3）模型参数，正则化参数、准确度阈值和核参数采用遗传算法来确定，即选取代表模型性能指标的均方误差（mean square error, MSE）作为适应度（fitness value）来迭代。

雨天场景下的进水流量图如图5所示。整个运行周期可分为2个阶段：前5日为第一阶段（晴天），此阶段的进水量在10000 m3~33000 m3区间平稳波动；从第6日开始为第二阶段（雨天），进水量有较大波动，可分为雨天早期、峰期和雨天后期。雨天早期因为滞后性雨量未反映到进水量，反而相对于晴天有所回落。随着雨天的推进，雨量开始反映到进水量，在第9日左右进入峰期，进水量爆发性地增加到50000 m3以上，并在30000 m3~ 50000 m3区间剧烈波动数日，这意味着反映水体质量的参数变量也将剧烈变化，这对模型是一个挑战，因为这需要模型在持续几天的新状态下给出目标变量的精准预测。随着雨天的消除（雨天后期），进水量逐步回落，并趋于平稳。考虑现实情况，污水处理在大多处于晴天场景下连续运行，数据也在晴天场景采集的较多。基于上述分析，用第一阶段采集的数据训练模型，第二阶段的数据测试模型，目的在于验证模型的泛化性能，以更好地反映实际运行场景。训练数据和测试输入数据在进入模型前（时差处理后）统一进行归一化处理。所有与输入变量相关的传感器在仿真运行过程中都是可靠的，以上处理方式着重于模型预测性能的变化，无需考虑其他影响因素。

图5 雨天场景下的进水流量图

图6(a)为本文所提方法的二次模型基于遗传算法技巧的参数搜寻结果。可以看出：当适应度值趋于稳定时，计算出的最佳参数= 0.7905，= 2.0180，= 0.0168。同理，图6(b)为主模型的参数搜寻结果，计算出的最佳参数= 23.8675，= 0.1545，= 0.0101。

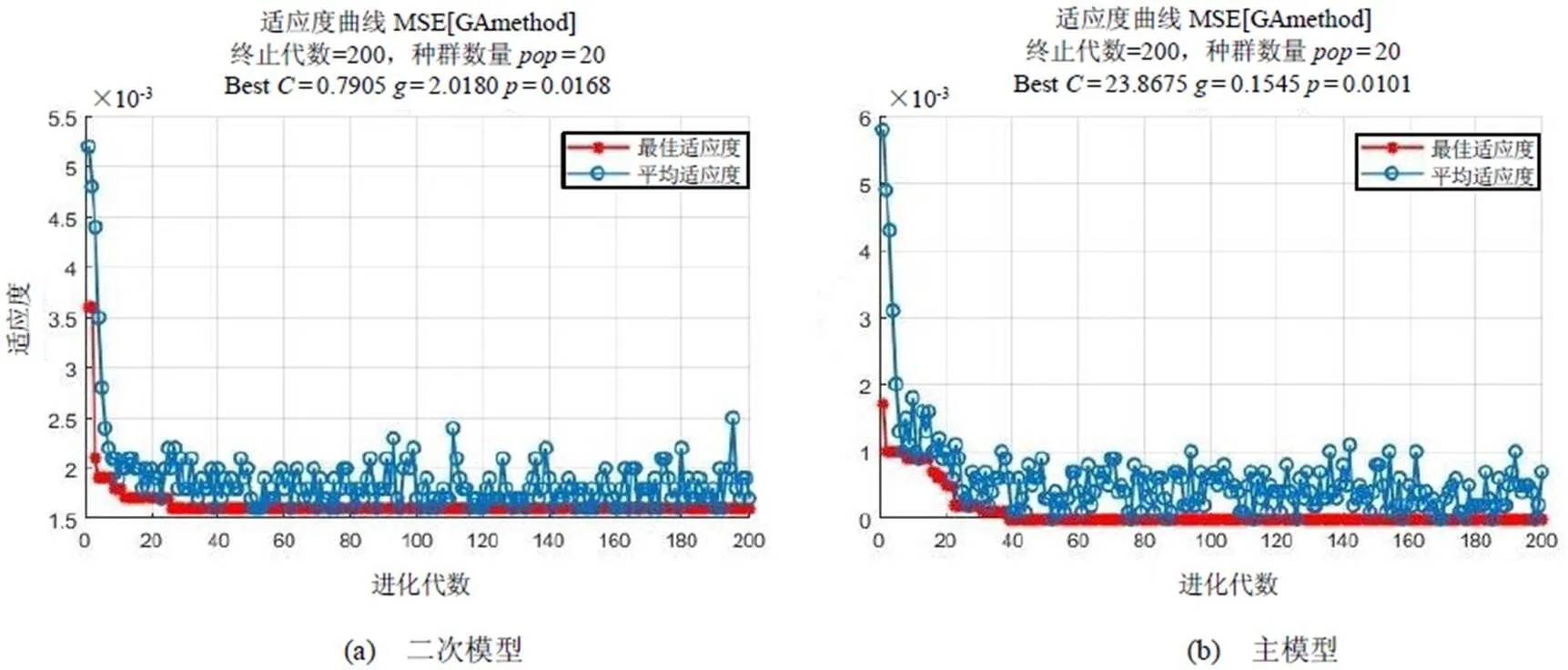
图6 适应度曲线

图7和图8为本文所提方法的预测结果。由图7可以看出：降雨期间目标变量CODe的预测值曲线紧密贴合实际值曲线，说明在剧烈干扰下本文所提方法能够很好地跟踪目标的变化趋势，评价指标和分别为0.7709和0.9953。由图8可以看出：基于二次模型提供的CODe信息，主模型对于BODe的预测总体上符合预期，预测值曲线不仅能够很好地跟踪实际值曲线的走势，且没有出现明显偏差；虽然在降雨峰期有些许波动，但考虑到剧烈外部干扰等因素的影响，其结果可以接受，评价指标和分别为0.0398和0.9987。

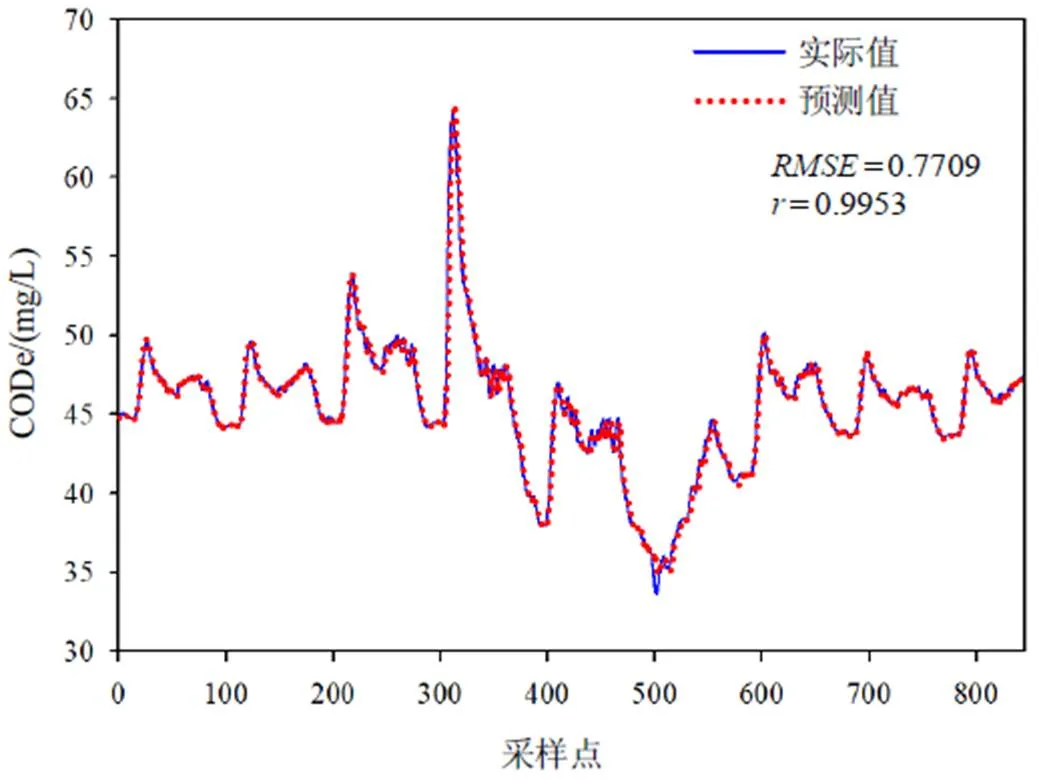
图7 二次模型预测结果

图8 主模型预测结果

在缺少CODe输入信息下的单模型SVR预测结果如图9所示。可以看出：CODe信息的缺失对模型性能产生了负面影响，主要表现在峰期结束后的一段时间无法跟踪到目标变化，且偏差较大；在其他时刻（峰期），预测结果也不太稳定，同样存在波动，无法很好地贴合实际值曲线，评价指标和分别为0.0566和0.9973。

图9 单模型SVR预测结果（缺少CODe信息）

具有实际CODe输入信息的单模型SVR预测结果如图10所示。可以看出：当具有确定、充足的输入信息时，模型对目标的预测结果令人满意，在降雨峰期以及峰期结束后的反复波动期间，都比前述2种模型表现优秀，评价指标和分别为0.0215和0.9966。

图10 单模型SVR预测结果（具有完整CODe信息）

3种测试模型目标变量的评价指标和结果如表2所示。

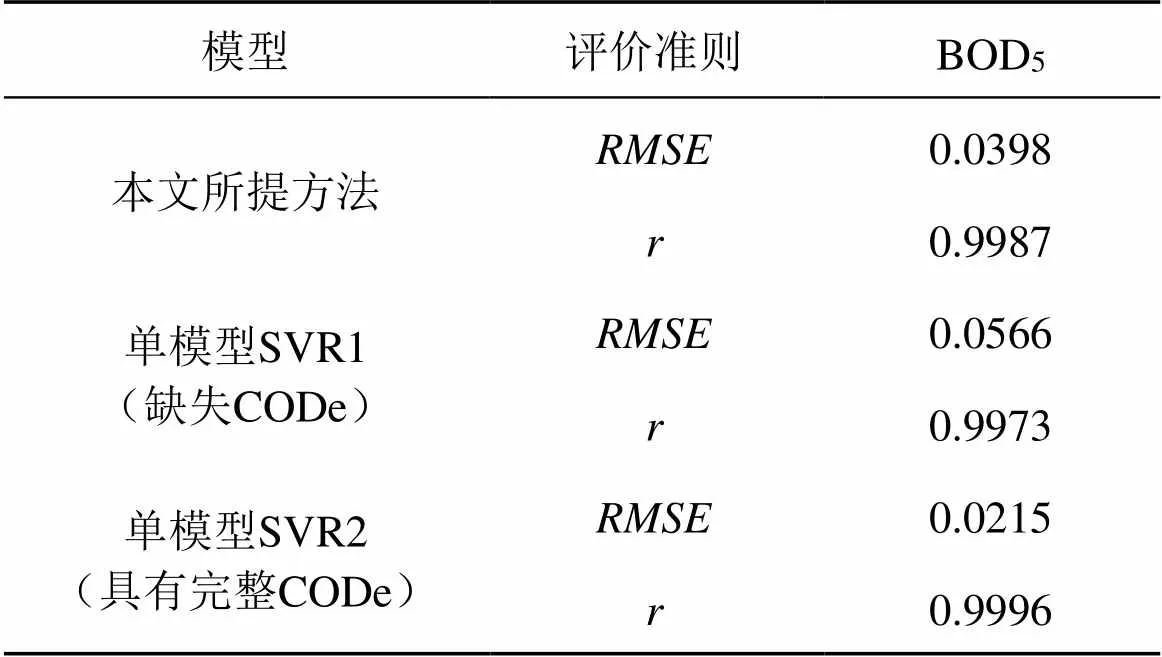
表2 3种测试模型目标变量的评价指标RMSE和r结果

4.3 讨论

本文通过案例验证了基于时差处理的自适应多层次软测量建模的有效性。基于BSM1仿真环境，对比模型在雨天场景下进行测试。结果表明：本文所提方法考虑了不易测的输入信息，对比缺失相关信息的单模型而言具有更好的预测表现；而对比具有完整输入信息的单模型，性能表现差距不大。综合结果分析有如下结论：

1）输入信息对于模型预测性能至关重要，多层次软测量建模方法考虑了与目标相关但不易测的重要输入信息，提高了预测表现力，从而在实际应用中更具优势；

2）与具有完整输入信息的单模型相比，多层次建模方法虽然在预测结果上略有不及，且存在计算负荷稍重等问题，但该方法易实现，且经济性高。对于大多数经费有限的中小型污水处理厂而言，在误差允许的范围内，以高经济性方式获得重要的水质参数是可行且可接受的。而完整的输入信息在实际操作中是不可行的，一些不易测量的变量无法作为正常获取的输入信息用于构造模型和预测，即使可获取也存在实现成本高昂等代价，难以在实际应用中推广。

5 结论

在污水处理过程控制中，多个难以获取的变量阻碍软测量建模，降低模型的预测能力。为此，本文提出基于时差处理的自适应多层次软测量建模方法。通过建立多个辅助模型以并联方式预测主模型建模所缺少的关键信息，从而有效提高主模型的预测能力。同时，采用时差建模方法，提高系统模型的自适应能力，解决模型性能退化问题。最后，通过一个仿真案例验证了本文所提方法的有效性。多层次建模方法可以进一步拓展到多个层次，其需求在于模型输入变量的不可获取性。

[1] 黄道平,刘乙奇,李艳.软测量在污水处理过程中的研究与应用[J].化工学报,2011,62(1):1-9.

[2] 曹鹏飞,罗雄麟.化工过程软测量建模方法研究进展[J].化工学报,2013,64(3):788-800.

[3] HAIMI H, MULAS M, CORONA F, et al. Data-derived soft-sensors for biological wastewater treatment plants: an overview[J]. Environmental Modelling & Software, 2013, 47: 88-107.

[4] KADLEC P, GABRYS B, STRANDT S. Data-driven soft sensors in the process industry[J]. Computers & Chemical Engineering (S0098-1354), 2009, 33(4), 795-814.

[5] 朱群雄,张晓晗,顾祥柏,等.基于特征提取的函数连接神经网络研究及其化工过程建模应用[J].化工学报,2018,69(3):907-912,883

[6] QIN S J. Recursive PLS algorithms for adaptive data modelling[J]. Computers & Chemical Engineering, 1998, 22(4-5): 503-514.

[7] 刘乙奇,黄道平,李艳.基于改进JIT算法的软测量建模及其在污水处理中的应用[J].华南理工大学学报(自然科学版),2011, 39(5): 55-60,67.

[8] 王功明,李文静,乔俊飞.基于PLSR自适应深度信念网络的出水总磷预测[J].化工学报,2017,68(5):1987-1997.

[9] QIU Y, LIU Y, HUANG D. Date-driven soft-sensor design for biological wastewater treatment using deep neural networks and genetic algorithms[J]. Journal of Chemical Engineering of Japan, 2016, 49(10): 925-936.

[10] 韩红桂,陈治远,乔俊飞,等.基于区间二型模糊神经网络的出水氨氮软测量[J].化工学报,2017,68(3):1032-1040.

[11] VAPNIK V N, VAPNIK V. Statistical learning theory[M]. New York: Wiley, 1998.

[12] 邱禹.面向污水处理的软测量建模研究及其应用[D].广州:华南理工大学,2018.

[13] BAGHERI M, MIRBAGHERI S A, BAGHERI Z, et al. Modeling and optimization of activated sludge bulking for a real wastewater treatment plant using hybrid artificial neural networks-genetic algorithm approach[J]. Process Safety and Environmental Protection, 2015, 95: 12-25.

[14] 李文静,李萌,乔俊飞.基于互信息和自组织RBF神经网络的出水BOD软测量方法[J].化工学报, 2019, 70(2): 687-695.

[15] HUNT K J, JOHANSEN T A. Design and analysis of gain-scheduled control using local controller networks[J]. International Journal of Control, 1997, 66(5): 619-652.

[16] 梅从立,杨铭,刘国海.基于证据合成的高斯过程回归多模型软测量方法[J].化工学报,2015,66(11):4555-4564.

[17] NARENDRA K S, BALAKRISHNAN J. Improving transient response of adaptive control system multiple models and switching[J]. IEEE Transactions on Automatic Control, 1994, 39(9): 1861-1866.

[18] 庞强,邹涛,丛秋梅,等.基于高斯混合模型与主元分析的多模型切换方法[J].化工学报,2013,64(8):2938-2946.

[19] HIROMASA K, KIMITO F. Adaptive soft sensor model using online support vector regression with time variable and discussion of appropriate hyperparameter settings and window size[J]. Computers & Chemical Engineering, 2013, 58(11): 288-297.

[20] 马建,邓晓刚,王磊.基于深度集成支持向量机的工业过程软测量方法[J].化工学报,2018,69(3):1121-1128.

[21] 吴菁,刘乙奇,刘坚,等.基于动态多核相关向量机的软测量建模研究[J].化工学报,2019,70(4):1472-1484.

[22] SOUZA F, RUI A, MENDES J. Review of soft sensor methods for regression applications[J]. Chemometrics and Intelligent Laboratory Systems, 2016, 152: 69-79.

[23] KANEKO H, FUNATSU K. Classification of the degradation of soft sensor models and discussion on adaptive models[J]. AIChE Journal, 2013, 59(7): 2339-2347.

[24] KADLEC P, Grbić R, GABRYS B. Review of adaptation mechanisms for data-driven soft sensors[J]. Computers & Chemical Engineering, 2011, 35(1): 1-24.

[25] 邱禹,刘乙奇,吴菁,等.基于深层神经网络的多输出自适应软测量建模[J].化工学报,2018,69(7):3101-3113.

[26] KANEKO H, FUNATSU K. Maintenance-free soft sensor models with time difference of process variables[J]. Chemometrics and Intelligent Laboratory Systems, 2011, 107(2): 312-317.

Self-Adaptive Multilevel Soft Sensor Modeling Method Based on Time Difference Processing

Qiu Yu1Ma Xingzao1Wu Jing2

(1. College of Mechanical and Electrical Engineering, LingNan Normal University,Zhanjiang 524048, China 2. School of Automation Science and Engineering,South China University of Technology, Guangzhou 510640, China)

In the process control of wastewater treatment, soft sensing is an effective mean to measure the difficult variables. However, the limitation of modeling input makes some variables that are related to the target but not easy to obtain unsuitable as input information, hindering modeling. Therefore, a novel multiple-level of soft sensor modeling method is proposed. First, multiple soft sensor sub-models are built using support vector regression to output sub-objectives which are related to the final objective variable but are hard to acquire. Then, the sub-objectives and original secondary variables are constructed as the inputs of the primary model to increase the information needed for the prediction, thus improve the final prediction effect. Meanwhile, a time difference modeling method is introduced in the modeling to deal with the performance degradation caused by external interference. The proposed method is validated through a case study of simulation and real application. The results show that Compared with single model SVR (lack of coder information) and single model SVR (with complete coder information), the method proposed in this paper has better prediction performance.is 0.0398,is 0.9987.

wastewater treatment; soft sensor; modeling; multilevel; self-adaptive

国家自然科学基金项目（51705228）；广东省教育厅项目（2017KQNCX123）。

邱禹，男，1988年生，博士，主要研究方向：软测量，过程控制。E-mail: qy-zq1988@163.com

马兴灶（通信作者），男，1984年生，博士，讲师，主要研究方向：智能控制。E-mail: maxz@lingnan.edu.cn

吴菁，女，1988年生，博士，主要研究方向：软测量。

TP 277

A

1674-2605(2020)05-0003-08

10.3969/j.issn.1674-2605.2020.05.003