基于程函方程反演的跨孔地震岩溶探测数值模拟研究*

2020-10-29石振明卢崔灿

工程地质学报 2020年5期

石振明卢崔灿刘鎏王尧彭铭

(①同济大学地下建筑与工程系，上海 200092，中国)(②同济大学岩土及地下工程教育部重点实验室，上海 200092，中国)(③佛罗里达大学土木与海岸工程系，佛罗里达 32611，美国)

0 引言

岩溶是水对可溶性岩石(碳酸盐岩、石膏、岩盐等)进行以化学溶蚀作用为主，物理侵蚀为辅的地质作用现象(张咸恭等，2000)。全球岩溶塌陷广泛分布，而我国岩溶地质面积约占国土面积的1/3(陈学军等，2019)。复杂岩溶地质环境中存在无规则岩溶分布与填充情况、复杂的岩溶水赋存条件、起伏的土岩界面(姚邦杰等，2019)，给大型工程的选址、设计、施工和运营造成极大的风险，探明地下岩溶分布具有重要意义。

目前，应用于工程中的岩溶探测地球物理方法可分为地表物探方法和孔中物探方法，前者包括高密度视电阻率法(Ei-Qady et al.，2005; 底青云等，2018)、地震反射法(Li et al.，2017)和高频面波法(夏江海等，2015)；后者包括跨孔弹性波CT法(朱文仲等，2008)、钻孔雷达法(Tan et al.，2012)、管波测试法(李学文等，2005)和桩底溶洞声呐探测法(石振明等，2016)。跨孔弹性CT法由于结合钻孔，其探测深度和精度较符合岩土勘察的需求，是适合岩溶强发育区的勘察方法。

基于初至旅行时的层析成像方法，由于其高效性，是目前近地表建模应用最广泛的方法。经典的初至层析反演方法基于射线追踪方程，在反演中需要显式计算炮点到检波点的旅行时及射线路径(Stewart，1991)，反演通常采用最小奇异值分解(LSQR)(Zelt et al.，1998)，迭代重构(SIRT)(Yang et al.，2009)等方法。而基于程函方程的层析反演方法仅需要计算初至时间场而不需要计算射线路径，借助伴随状态方法求取模型更新量，在复杂区域理论上具有更好的反演效果，更适合岩溶强发育区的探测(Plessix，2006)。

本文针对跨孔地震波岩溶探测，展开了基于程函方程的层析反演的数值模拟研究。利用高阶时域有限差分解弹性波方程，考虑多种岩溶发育工况，模拟现场实测数据，并对模拟数据进行基于程函方程的层析反演，验证了该方法在跨孔岩溶探测中的有效性，并讨论了其局限性和未来研究方向。

1 数值研究方法

基于程函方程的初至层析反演是一种以程函方程作为反演中的正演方法的成像技术。本文的数值研究思路如图1，先设置真实模型，用时域有限差分计算得地震记录，模拟现场观测数据，从地震记录中提取初至旅行时；然后设置初始模型，基于程函方程计算时间场，计算旅行时残差，并更新模型，将更新模型作为新的初始模型代入，最后重复迭代算法直至满足迭代终止条件，得到最终的反演地层速度模型，用于岩溶地质的识别。

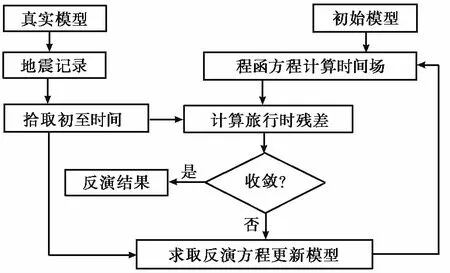
图1 基于程函方程的跨孔地震岩溶探测反演研究思路

1.1 正演方法

根据以下二维弹性介质中的弹性波方程模拟跨孔地震波探测过程：

(1)

式中：x，y为两个方向的直角坐标；t为时间(s)；ρ为密度(kg·m-3)；vx，vy分别为质点振动速度在x，y两个方向上的分量(m·s-1)；σxx，σyy，σxy为应力分量(N·m-2)；fx，fy为体力在x，y两个方向上的分量(N·m-3)；σxx0，σyy0，σxy0为表面力分量(N·m-2)；λ，μ为拉梅常数(N·m-2)(Landau et al.，1986)。

利用高阶交错网格的时域有限差分解弹性波方程，将应力分量和速度分量分别定义在两套网格上，并引入半网格点，在半网格点上进行空间导数的计算，即在网格上进行线性应力速度关系的离散化和动量方程的离散化。正演的初始时间所有网格点速度和应力均为0。为提高计算效率，必须引入完全匹配层(PML)作为吸收边界，在吸收层内部设置衰减因子对波场进行衰减。

1.2 基于程函方程的初至层析反演方法

旅行时层析反演方法是通过迭代计算寻找正演旅行时与观测旅行时之间差异最小的地层参数模型(郭振波等，2019)，其目标函数可定义为正演和观测旅行时之差的最小二乘如式(2)：

(2)

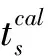
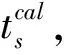
t(x)·t(x)=s2(x)

(3)

式中：t(x)为波场从源点到空间任意点x的旅行时；s(x)为x处的慢度。利用迎风有限差分对式(3)进行离散之后的形式如式(4)：

(Dxts)(Dxts)+(Dyts)(Dyts)=diag(m)m

(4)

生产力的发展是社会文明形式的最终决定力量。换句话说，每一种社会文明都不是凭空而来无缘而去，说到底还是有社会生产力的发展水平所决定的。生产力大发展过程实际上是生产力不断积累过程，他的发展是川流不息的，他不会因为某个阶段的消灭而消灭，也不会因为某种社会形态的消亡而消亡。当生产力发展到一个更高的阶段，原有的旧的社会文明形态已经不适应社会生产力的发展，于是就将逐渐被淘汰，社会就将诞生新的文明形式以适应生产力的发展，同时这种新的文明形式将随着生产力的继续发展而不断成长壮大。生态文明的诞生和发展，就是生产力发展到新的阶段的必然要求。

(5)

将式(5)带入目标函数式(2)后对介质参数m求一阶导数如式(6)：

(6)

若先对式(4)中m在等式两侧求导，可先得到：

(7)

将式(7)代入式(6)，可得基于程函方程的层析反演的目标函数的一阶导数为：

(8)

如想得到目标函数O(m)的最小值，其一阶导数应等于0，即需要找到适合的介质参数m使得g=0; 可以将式(2)在m0处进行二阶泰勒展开后对m求导，并令其等于0。可得到：

δm=-(H|m0)-1g|m0

(9)

式中：H为目标函数对介质参数的二阶导数，即Hessian矩阵。

式(8)结合式(9)经整理(Taillandier et al.，2009)可得其等价形式非线性迭代求解式(10)。

(10)

利用高斯-牛顿法求解式(10)，在求解过程中Hessian矩阵近似为单元矩阵(即最速梯度法)。从而得到介质参数m更新量，在反演迭代过程中，速度模型不断更新，程函正演的初至旅行时与从观测记录中提取的初至旅行时的残差逐渐减小，当残差小于设定值时即满足迭代终止条件时，停止迭代，此时的速度模型即最终反演结果。

2 数值试验

岩溶最基本的两种发育形态为溶洞和断层，因此数值试验设置了单一溶洞、单一断层、溶洞断层组合、多溶洞组合共4组工况。4种不同的地质体组合的工况以均质地层为背景，在地层中有两个深度为10im，其相邻水平间隔为10im的钻孔，地层的材料参数如表1。在模型的左侧钻孔中布置了一排竖向间距为0.5im的发射器，共20个，震源是中心频率为3ikHz的Spike波。模型的右侧钻孔中布置了一排竖向间距为0.2im的接收器，共50个。

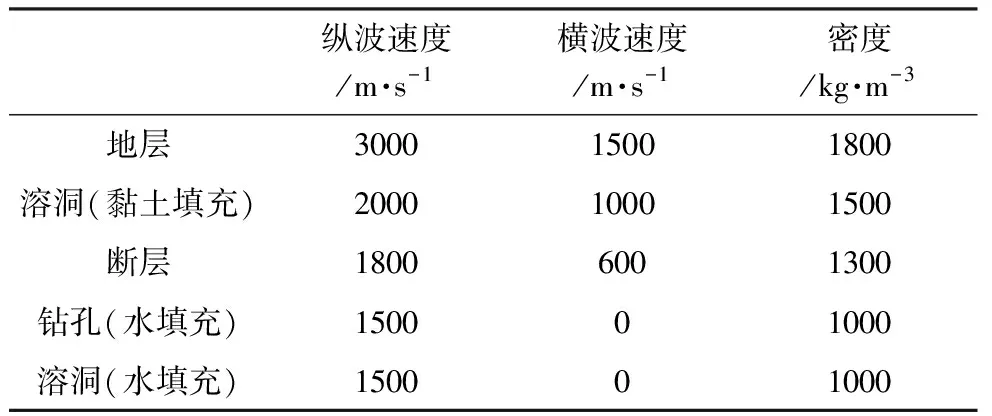
表1 地层参数设置

2.1 工况1：单一溶洞

图2为单一溶洞正反演结果。其中：图2a表示正演模拟的真实模型；由图2a用时域有限差分计算可得地震记录如图2c、图2d，分别代表从上到下第1炮(深度为0.5im)、第20炮(深度为10im)x分量的地震记录，以此模拟现场观测记录；从地震记录中提取初至旅行时，得到图2e中的观测旅行时；图2b表示反演的初始模型；将程函方程作为反演中的正演方法，由图2b可计算得到图2e中的正演旅行时，比较图2a 与图2b，发现在反演前图2e中的观测旅行时和正演旅行时差别较大；在反演过程中，通过多次迭代，更新速度模型，并更新正演旅行时，可以看到图2h中标准化残差随着迭代次数增加而不断减小，最终满足标准化残差小于0.005的迭代终止条件，得到图2f迭代结束后旅行时，图2g最终反演结果。

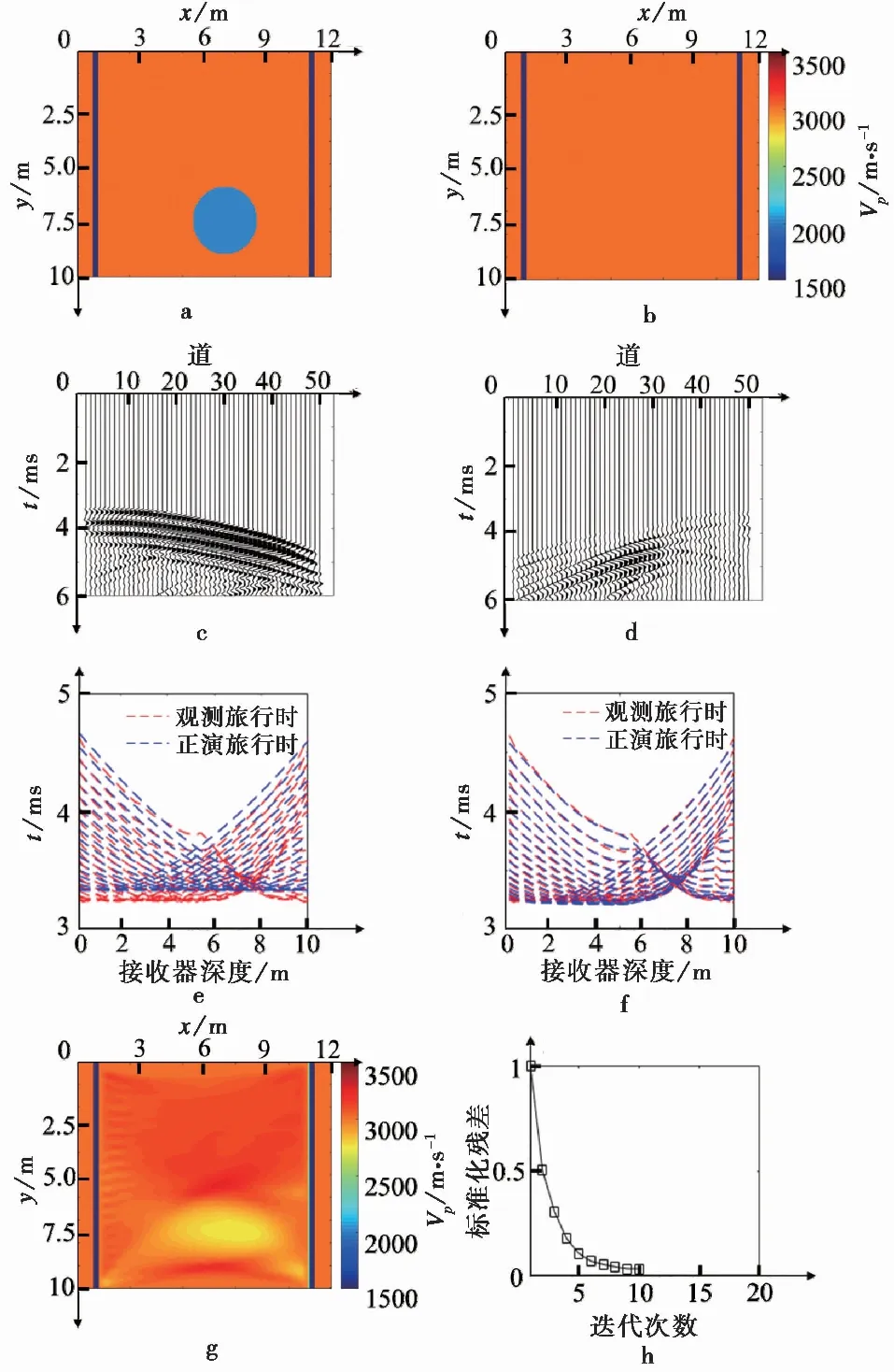
图2 工况1：单一溶洞试验结果图

对比图2a 和图2g可以看出，反演结果揭示了钻孔间深度6～9im处有一溶洞发育，其填充物速度明显低于背景地层。基于程函方程的反演基本揭示了溶洞的位置、大小和形状，反演迭代次数为10次，收敛迅速。就溶洞的形状而言，反演的纵向分辨率略高于横向分辨率。同时，洞中填充物的波速较真实模型偏高。

2.2 工况2：单一断层

单一断层的反演数值研究过程如图3a～图3h所示。在真实模型中设置一倾斜的线性断层，深度发育在1～4.5im，断层内填充含水的低速体。反演经过了15次迭代达到了收敛。对比图3a 和图3g可以看出，反演结果成功揭示了断层的方向和位置，反演结果中断层填充物的波速较真实模型偏高。与工况1的反演结果相比，图3g中有较多的伪像，相比溶洞，初至旅行时层析反演对断层较不敏感。

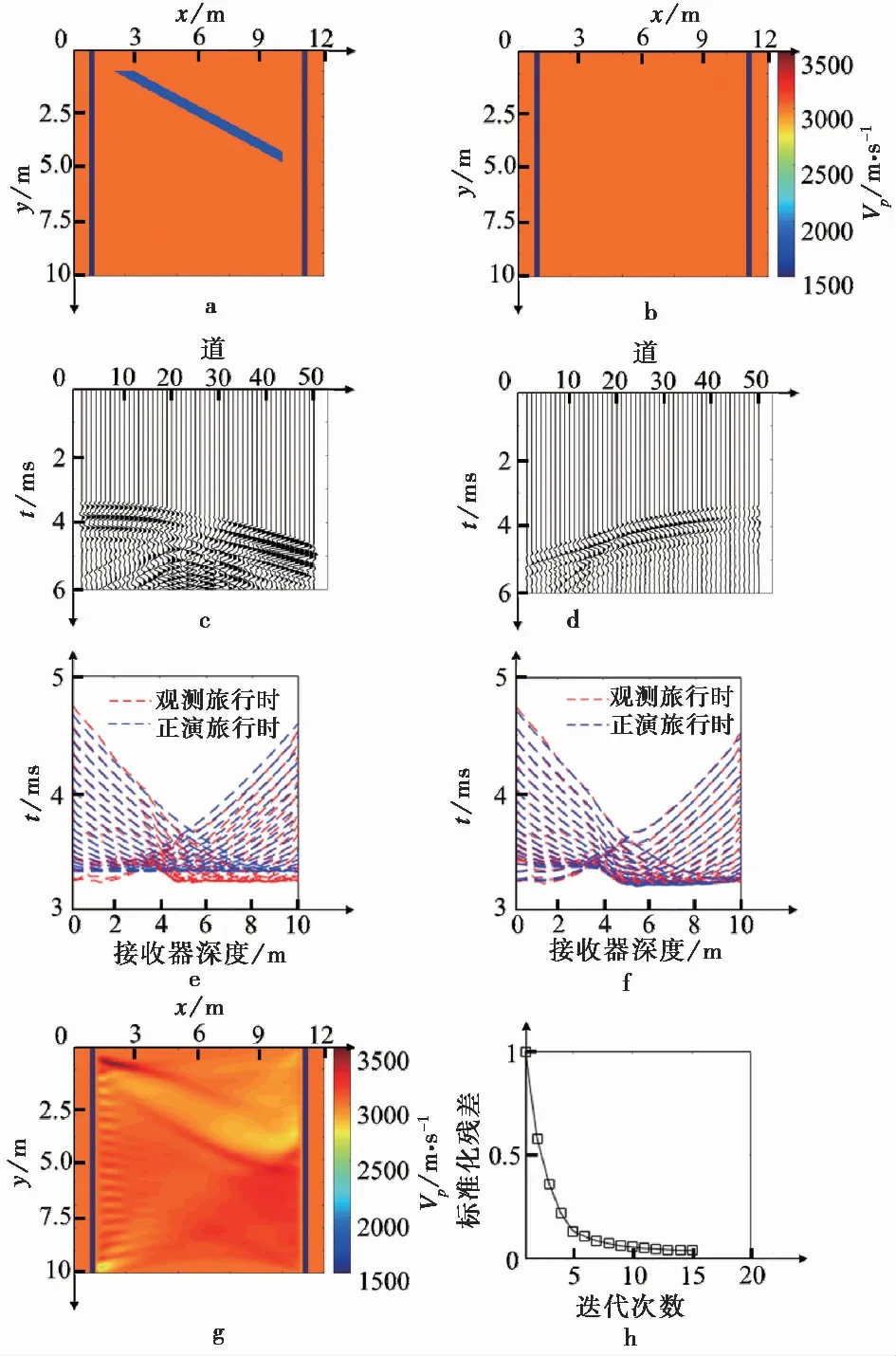
图3 工况2：单一断层试验结果图

从理论上解释，这是因为经过断层的最短射线路径相对溶洞较小，尽管断层的反射波对整个地震记录上产生了很大变化，但是由断层产生的初至旅行时变化较小，导致初至层析反演过程中容易陷入局部最优解的问题。

2.3 工况3：溶洞断层组合

为了研究基于程函方程的跨孔层析反演方法对多个异常体同时成像的效果，工况3组合了工况1和工况2的两种岩溶地质体，在工况3模型中设置了相同的溶洞和断层。通过对比图2、图3和图4可以看出工况3的地震记录、反演结果与工况1和工况2叠加的结果相似，溶洞与断层的存在对各自反演结果的相互干扰较小。同时工况3的迭代次数并没有随着模型变得复杂而明显增加，收敛速度与前两个较简单工况相当，表明基于程函方程的跨孔层析反演方法对于复杂地质条件的反演具有较好的稳定性。

图4 工况3：溶洞断层组合试验结果图

同时也注意到图4a 中，真实模型中断层中填充物的波速低于溶洞中填充物的波速，而在图4g中，反演的断层中填充物的波速却高于溶洞中填充物的波速，更接近地层背景波速，这也验证了该初至旅行时的反演对断层较不敏感，反演成像精度没有溶洞高。

2.4 工况4：多溶洞组合

串珠状溶洞是典型的复杂岩溶地质现象，往往在单一钻孔中会揭示多个溶洞的存在。工况4设置了多个溶洞，并考虑了不同填充物和形状，以讨论该方法对多个溶洞不同方面的成像效果。

其数值研究过程如图5所示，对比图5a与图5g发现，反演结果有效区分了两个不同溶洞的深度和水平位置、形状、大小和填充物速度的高低。反演的迭代次数有所增加(16次)，但依然可以在短时间内完成。同时对比图2g、图5g 可以看出两个溶洞的存在对反演结果的相互干扰较小。反演依然存在低速异常体反演速度比真实速度高的问题。且横向分辨率明显没有纵向分辨率高，这与射线密度有一定关系。

图5 工况4：多溶洞组合试验结果图

根据4个工况的数值试验结果，可知钻孔间的溶洞和断层等速度异常体对地震记录影响很大，其中溶洞对初至旅行时的影响更为明显。初至旅行时类的反演方法因为只提取初至信息，忽略了波形信息，反演速度较快，在不到20次迭代中均可以将标准化残差降低至0.005以下，得到孔间岩溶异常体的分布。但由于仅仅提取初至时间，没有充分利用反射波和透射波信息，对于突变型的地质异常体，往往反演为一个速度渐变的异常体，这也导致：反演速度比真实速度偏高，更接近背景波速；其异常体的实际横向尺寸偏大。但考虑到基于程函方程的跨孔层析反演方法在多个岩溶地质体共存的复杂地质条件下依然可以保持高效和稳定，该方法可以为实际工程提供重要勘察信息。