静力触探识别场地土层分布的贝叶斯学习方法研究*

胡 越 王 宇

(香港城市大学建筑学及土木工程学系，香港 999077，中国)

0 引 言

地层结构是复杂且漫长的地质作用的结果，在空间上呈现出变异性。在岩土工程勘察中，准确表征地层结构及其空间变化规律对岩土工程设计、分析和施工尤为关键。静力触探试验(CPT)是实际工程中常用的一种原位测试方法。CPT将带有传感器的触探杆匀速压入试验土层，通过连续测量锥尖阻力qc，侧摩阻力fs，孔隙水压力u等数据，来确定场地土体的物理力学特性随深度的变化。由于不同种类的土层物理力学性质有明现差异，在穿越不同种类的土层时CPT数据曲线会发生明显的变化。故利用CPT数据曲线可有效地识别相邻土层的边界。近年来，国内外众多学者对基于CPT的土体分层分类方法进行了大量研究。刘松玉等(2013)认为CPT在实际工程中能够准确地对土体进行分类并划分土层边界。蔡国军等(2009)应用聚类分析理论对若干典型场地的CPT数据进行了土体分层研究。Robertson(2009)根据大量CPT实测数据提出基于土的行为特性的土性分类标准。Hegazy et al.(1996)和Tumay et al.(2008)采用模糊理论对CPT数据曲线进行土层分界和土体分类。Wang et al.(2013)提出了一种贝叶斯方法对CPT数据曲线进行分层。

CPT通常是在一个设计勘探位置垂直于地表进行的。大部分对于CPT的研究都只针对于单一CPT探测点沿深度方向的数据。真实的地层结构往往在水平方向亦呈现出变异性。而实际工程中，由于时间和预算的限制，工程场地中的CPT探测点数量有限且分布稀疏。如何准确推测CPT探测点之间大部分未测区域的数据和分层情况是岩土工程勘察中棘手的难题。例如，在实际工程常用的二维地质剖面中，工程师通常直接线性连接有限勘测点的分层情况(图1)。这种简化处理忽视了实际土体情况的复杂空间变化。而且，这种简化的边界连接方法无法处理相邻勘探点层数不统一的情况。例如在图1中，CPT1中确定了黏土，粉质黏土，砂质粉土和砂土共4种类型的土。而CPT2中仅确定了黏土，砂质粉土和砂土而没有粉质黏土。此现象同样出现在CPT3和CPT4之间。如图1所示，对于这类情况，此二维地质剖面中存在两个非常不确定的三角形区域。传统的地统计方法也不足以解决此类问题。主要因为传统的地统计方法的实现需要假定数据的平稳特性，而对于多种类土而言，土体性质显然不具有平稳特性且有较大的差异。另一方面，由于测量数据过于稀疏，准确估计水平方向的地统计模型参数十分困难。以上可见，基于稀疏勘探点准确绘制二维地质剖面仍是工程勘察中的难题。

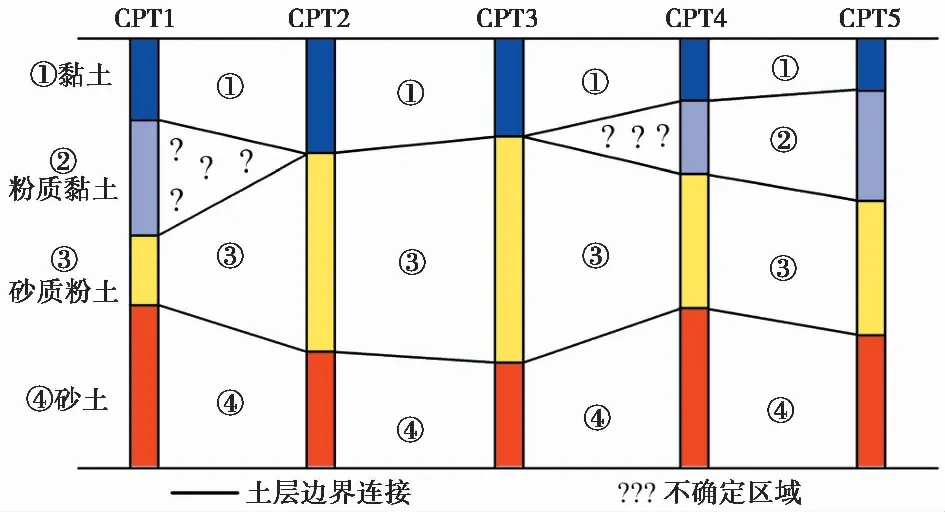
图1 二维地质剖面土层分布推测问题

针对上述问题，本文提出了一种数据驱动且非参数化的贝叶斯学习方法。它可利用有限且稀疏的CPT勘探点来推测二维地质剖面中的土层分布情况。此方法不需要假定传统地统计方法中的自相关函数模型，也不需要估计自相关函数的参数。本文阐述了此方法的具体流程并用模拟算例进行方法论证。

1 方法介绍

机器学习方法近年来随着计算机硬件性能的提升迅速发展。与传统基于物理机理的模型相比，机器学习方法跳过了探明物理机理的过程，而通过学习现有数据特征或经验直接给出优化的预测模型(许冲等，2019；鄢好等，2019)。在岩土和地质工程领域，基于已有勘探点的数据预测未勘探区域的数据可看作是一个机器学习问题。周翠英等(2019)利用机器学习方法进行了地层序列模拟。Wang et al.(2017)利用极限学习机与主成分析进行了地质储层厚度预测。通常情况下为保证预测模型的质量，机器学习算法需要训练相当的数据量。而在实际的岩土工程中，勘测数据数量有限且分布稀疏。本文提出了一种贝叶斯学习方法，可利用少量CPT勘探点自动识别二维剖面中的土层分布。贝叶斯学习方法是利用贝叶斯理论求解机器学习问题的方法。贝叶斯框架可利用先验概率信息来辅助推测。此方法包括3个主要部分：(1)基于贝叶斯学习的CPT数据二维插值；(2)利用Robertson土性分类图确定土性分类；(3)土层边界自动描绘。此方法不需要构建参数化的自相关函数来模拟CPT数据的空间变化特征。

1.1 基于贝叶斯学习的CPT数据二维插值

假设某个二维地质剖面内的真实CPT数据可用一个维度为Nx1×Nx2的矩阵F来表示。矩阵中每一个元素代表剖面中某个位置的CPT数据。在本文的贝叶斯学习方法框架下，F可表示为一系列与F同形的基函数矩阵的权重叠加，表达式为：

(1)

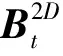
(2)

(3)

(4)

利用以上方法，可从少量CPT勘探点直接插值得到完整的CPT数据二维剖面。不同土层的CPT数据不需要做去趋势的预处理。本方法亦可考虑模糊的土层边界或过渡层的影响。

1.2 确定二维剖面的土性分类

基于CPT数据，可通过Robertson土性分类图来确定土体分类。本文中采用的是Robertson(2009)提出的基于归一化CPT数据的土性分类图(图2)。图中的归一化摩阻比FR和归一化锥尖阻力Qt的表达式为：

(5)

式中：σv0和σ′v0分别为土的竖向总应力和竖向有效应力；qt为修正后的锥尖阻力。图2中的土性分类图总共划分了9个区域。分别对应了从灵敏细粒土到细粒极硬砂的共9种土性类别(SBT)。通过查看任一(FR，Qt)数据对的位置，可确定其对应的SBT值。同理，利用以上插值方法分别得到的FR二维剖面和Qt的二维剖面，可导出SBT的二维剖面。本文暂未考虑Robertson土性分类图的模型不确定性。Hu et al.(2020)利用概率模型考虑了Robertson土性分类图的模型不确定性。

图2 土性分类图

1.3 土层边界自动描绘

以上得到的SBT二维剖面包含了完整的地层分布推测信息。此方法亦可自动地描绘SBT二维剖面中的土层边界位置，从而得到一个简洁的场地表征。SBT二维剖面中SBT数值发生突变的位置一般可认为是不同土层之间的分界面。例如在图3a的SBT二维剖面中，砂土层和粉质砂土层之间有一条用黑实线示意的分界面。在此分界面的位置，SBT值发生了突变。描绘SBT二维剖面中的土层边界即等同于标记所有SBT值发生突变的位置。在图像处理领域，边缘探测方法可用来直接标记SBT二维剖面中SBT值发生突变的位置(Canny 1986)。边缘探测方法的数学本质是在找寻图像亮度的梯度最大值位置。使用常见的边缘探测工具，例如Canny滤波器与SBT二维剖面卷积，可得到SBT二维剖面的梯度图。梯度最大的位置即为土层边界。例如在图3b中，梯度最大的位置标记为“Y”。利用此边界探测方法，可自动描绘出SBT二维剖面中的土层边界位置。

图3 土层边界自动划分示例

2 模拟算例

本节探讨一个模拟的二维地质剖面算例如图4所示。此二维剖面厚度为12.7im，宽度为25.5im。剖面中存在有黏土(第1层)，粉质黏土(第2层)，砂质粉土(第3层)和砂土(第4层)共4种类型的土。其中第1，3，4层在水平方向贯穿了整个剖面，而第2层只在剖面的左右两边局部区域出现。这种地质条件即可导致类似于图1中的相邻勘探点土层数量不一致的情况。

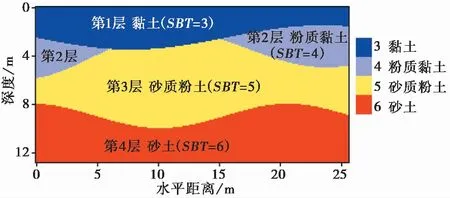
图4 模拟二维地质剖面

鉴于实际情况下，地质剖面通常是未知的，此二维地质剖面算例仅用作演示和验证目的。在每个土层中，FR和Qt的数据都由随机场生成器产生。两个方向的数据精度都为0.1im。表1汇总了所采用的随机场模型参数，包括平均值，标准方差，空间相关长度。所生成的一组二维FR和Qt地质剖面如图5所示。FR和Qt的二维剖面都是维度为128×256的矩阵。这组二维FR和Qt地质剖面可看作是某个特定场地的地质条件表征。假设在此剖面中，布置了M=5个CPT勘探点，如图5中虚线所示。这5个CPT勘探点的数据曲线如图6所示，无论是FR还是Qt数据曲线都表现出高度的变异性。多土层的数据表现出非平稳的特性。

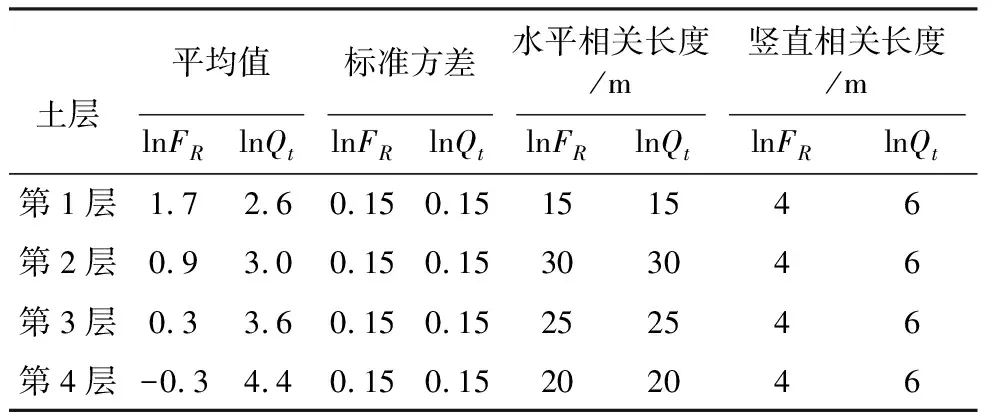
表1 模拟地质剖面随机场参数

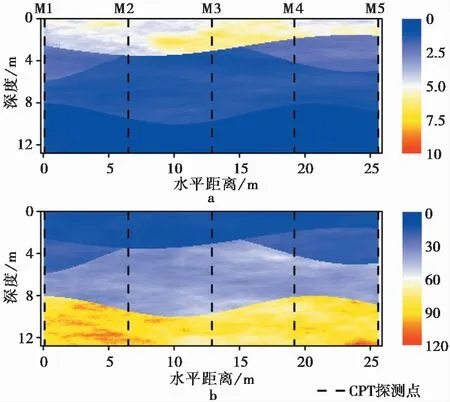
图5 模拟FR和Qt二维剖面

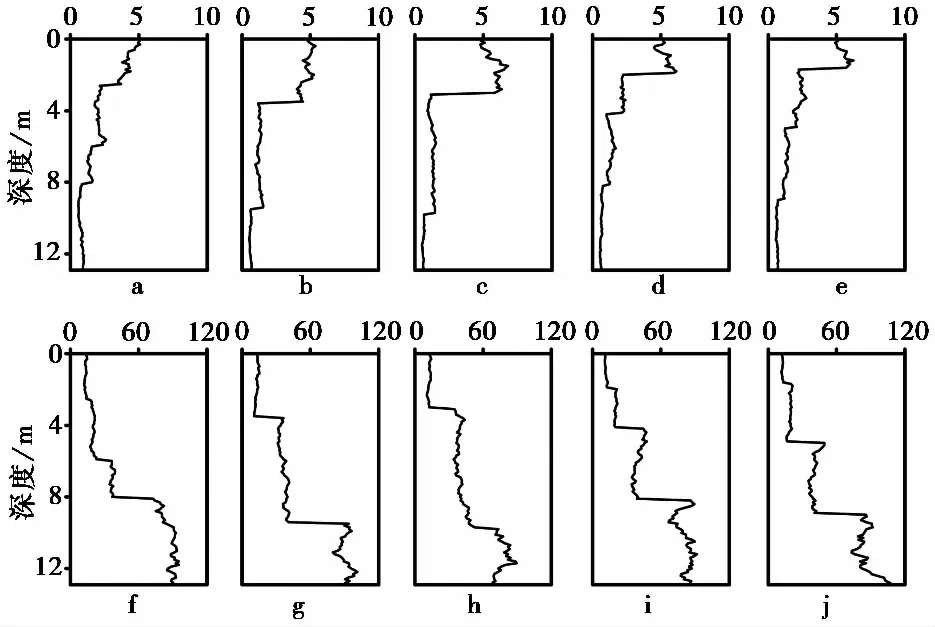
图6 M1～M5的数据曲线

分别对FR和Qt构建Y矩阵后，即可用贝叶斯学习方法直接对FR和Qt数据进行二维插值。插值结果如图7所示。FR和Qt的插值结果都是维度为128×256的矩阵。通过比较图7和图5可以看出，贝叶斯学习方法得出的插值结果和原数据相似。其中的数据非平稳特性和各向异性都合理体现。为了更清楚展现插值结果，4个检测位置(U1～U4)的插值数据曲线如图8所示。这4个检测位置如图7中的点线所示。可以看出，这4个检测位置在相邻CPT探测点位置的中间，即是对插值效果最不利的位置。而从图8中可以看出，插值结果的总体变化趋势和对应的原始数据非常一致。贝叶斯学习方法可给出合理的插值结果。

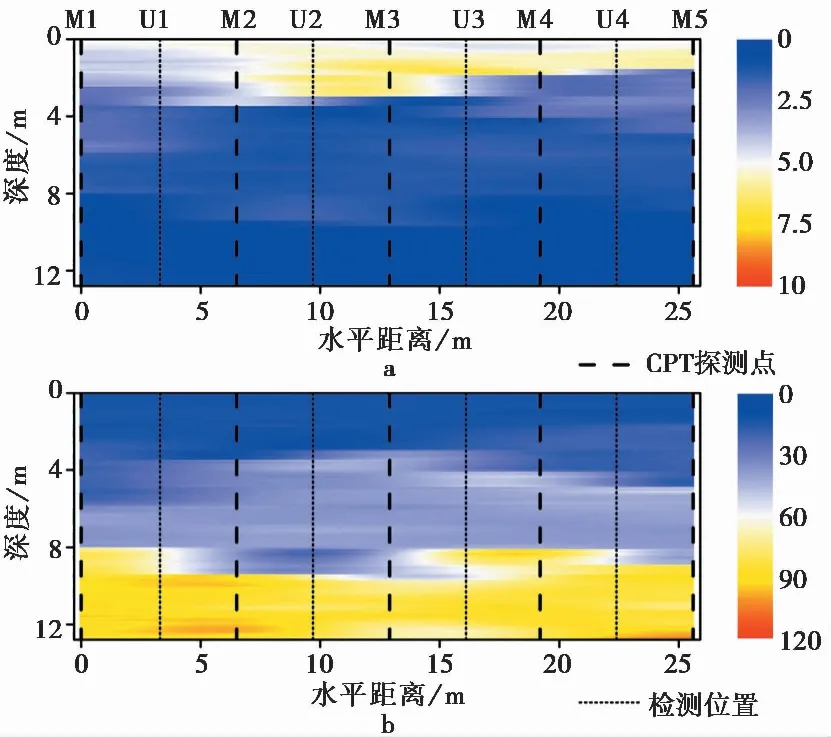
图7 基于5个CPT探测点的插值结果

图8 检测位置的插值效果对比

利用插值后的FR和Qt二维剖面和Robertson土性分类图(Robertson, 2009)，可确定二维剖面内每一点的土性分类。基于图7中插值结果的SBT的二维剖面如图9a所示。在图9a中，黑实线表示此模拟算例的原始边界。从图9a中可以看出，本方法推测的SBT二维剖面的土层分布基本符合原始的土层分布。为了更清楚展现土层分布估计结果，4个检测位置(U1～U4)的土层分布情况如图10a所示。在图10中，原始的SBT值表示为黑色十字符号，对应的推测结果表示为红色方块。从图10a中可以看出大部分的红色方框都与对应的黑色十字重合，即说明本方法的土层推测效果较好。此外，本研究还量化地分析了土层推测的准确性。准确度量化指标定义为某一土层内正确估计的点数与该层内总点数的百分比。如表2中的第3列所示，当只有5个CPT探测点时，二维剖面的总体的估计准确度为92.9%。结果表明，本方法的估计准确度高。第2层土(粉质黏土)的估计准确度相对其他土层偏低。这是由于第2层土只局部存在于剖面两侧，相对其他土层来说面积最小，对插值结果也最为敏感。而且在5个探测点中只有3个探测点有探测到第2层土的信息，其准确度也受到统计不确定性的影响。

图9 二维剖面土层划分结果

图10 检测位置的土体分类结果

表2 CPT 探测点数量对估计结果准确度的影响

利用边界探测方法，可自动描绘SBT二维剖面中的土层边界位置。在此算例中使用Canny滤波器与SBT二维剖面卷积，可得到SBT二维剖面的梯度图，如图9b所示。红色点标记了其中梯度最大的位置。从图9b可看出，描绘的边界和原始边界基本相符。本方法给出了合理的土层分布推测和土层边界划分。图1中的土层分布推测问题可得到有效解决。

3 勘探点数量的敏感性分析

勘探点数量对岩土工程勘察有显著的影响。本节探讨了勘探点数量对本方法效果的影响。假设在以上模拟算例的二维剖面中，布置了M=15个CPT勘探点(如图11中虚线所示)，并用这15个勘探点的数据重复以上的流程。本方法推测出的SBT二维剖面如图11所示。从图11可以看出，当CPT勘探点数量增加，本方法推测出的结果趋于准确。SBT二维剖面中的土层边界几乎与原始边界重合。在这种情况下，4个检测位置(U1～U4)的土层分布情况如图10b所示。从图10b中可以看出几乎所有的红色方框都与对应的黑色十字重合。表2中第四列亦表明二维剖面的估计准确度显著提高。本方法的效果是数据驱动的，当可用勘探点数据增多，推测的土层分布结果可收敛至真实情况。

图11 基于15个CPT探测点得出的SBT二维剖面

4 结 论

(1)基于贝叶斯学习算法，提出了一种新的基于静力触探的场地分层方法。相比传统的地统计方法，此方法是非参数化的。此方法不需要假定自相关函数模型，也不需要估计自相关函数的参数，可利用少量的CPT探测点直接给出二维地质剖面中的土层分布。不同土层的CPT数据不需要做去趋势的预处理。模拟算例的结果表明，此方法可给出准确合理的结果。

(2)通过勘探点数量的敏感性分析，发现此方法具有数据驱动特性。当勘探点数据增多，推测的土层分布结果可收敛至真实情况。