平面交叉裂隙非线性渗流模型参数人工神经网络预测*
2020-10-29毋振华王者超郭玟志
毋振华 王者超 郭玟志 杨 斌 刘 杰
(东北大学资源与土木工程学院,沈阳 110819,中国)
0 引 言
岩体内部发育的裂隙对于岩体的物理性质有着较大影响(董艳辉等,2019;赵建军等,2019)。同时,岩体内部发育的裂隙网络是水和其他流体流动的主要通道(刘日成等,2016)。裂隙网络渗流对工程活动的影响是一项十分重要的基础研究,其在地下水封油库(李玉涛等,2019)、二氧化碳封存、水利水电工程、计算地下流场分布、判断工程稳定性等方面有重要作用。
岩体裂隙网络主要由单裂隙和交叉裂隙组成(速宝玉等,1997),单裂隙和交叉裂隙的渗流规律已经有许多学者进行过相关研究。在单裂隙渗流方面,Berkwoitz(2002)通过测量数据分析、流体数值模型等方法对单裂隙渗流规律进行了研究。Zimmerman et al.(1996)研究了岩石粗糙单裂隙的渗流现象,讨论了用润滑方程或Hele-Shaw方程代替Navier-Stokes方程时需要满足的几何条件和运动学条件等。在交叉裂隙渗流方面:朱红光等(2015)通过COMSOL数值模拟,探究了交叉裂隙渗流的过量压力降及其产生原因。刘日成等(2016)运用染色流体在光滑模型的流动研究了交叉裂隙的渗流规律。Johnson et al.(2006)运用染色流体在粗糙裂隙模型中的流动,得出交叉裂隙能促进流体在交叉位置的混合。李博等(2019)通过随机方程模拟裂隙粗糙程度,运用数值模拟等方法确定了交叉裂隙溶质混溶方式。詹美礼等(1997)运用有限元方法从N-S方程出发研究交叉裂隙水流的基本特征。刘杰(2019)利用数值模拟和实验的方法得到了交叉裂隙几何条件与交叉裂隙非线性渗流模型非线性参数的数值表达式。
上述研究成果大多从定性角度研究交叉裂隙的渗流规律,没有定量分析交叉裂隙几何条件和非线性渗流模型参数之间的关系。本文借鉴刘杰(2019)的交叉裂隙渗流模型,利用人工神经网络具有处理不确定数值关系和逼近复杂非线性系统的能力,采用人工神经网络方法建立交叉裂隙几何条件与非线性系数之间的定量关系。将人工神经网络引入交叉裂隙渗流规律的研究,为交叉裂隙渗流规律的研究提供了新方法。
1 交叉裂隙渗流规律
Forchheimer方程已被验证适用于描述孔隙和裂隙介质的非线性渗流特征(Forchheimer,1901)。
P=AQ+BQ2
(1)
式中:A和B分别为线性项和非线性项系数。线性项表示流体中黏滞力造成的能量损耗,非线性项表示流体中惯性力造成的能量损耗,系数A、B和交叉裂隙的开度、长度、粗糙度等几何条件相关。
Forchheimer方程需要确定线性系数A和非线性系数B。因此,Chen et al.(2015)建立了Forchheimer方程的参数表达式。
(2)
式中:μ为黏滞系数;ρ为流体密度;g为重力加速度;w为模型宽度,本研究中取1im。
裂隙网络中存在单裂隙和交叉裂隙。单裂隙的非线性渗流规律可用Forchheimer方程进行表达,而交叉裂隙的渗流规律也有线性项和非线性项,针对交叉裂隙分支数较多的情况,根据Forchheimer方程进行推导,得到了交叉裂隙的渗流规律。交叉裂隙的渗流规律应用矩阵形式表达(刘杰,2019)。
(3)
根据数值模拟结果分析了低流速区间的数据(图1),发现低流速区间符合立方定律,因此[A|B]ij中的线性系数可用式(2)求得。而非线性系数由于交叉裂隙几何条件的不同而不同。因此,非线性系数采用数值模拟和回归拟合获得。本文的研究内容是分析交叉裂隙几何条件与非线性系数之间的规律。

图1 压差与入口流量线性区域对比图
2 非线性参数人工神经网络预测方法
2.1 人工神经网络预测原理
人工神经网络能够处理复杂的非线性和不确定关系,是一种强大的数据处理方法。交叉裂隙渗流模型非线性系数与交叉裂隙几何条件的关系是不确定的、非线性的,与人工神经网络处理数据的特点相适应,故采用人工神经网络方法来进行数据处理。
人工神经网络包含输入层、隐含层及输出层(图2)。输入层用于输入数据的自变量(交叉裂隙开度、不同裂隙分支角度)。层与层之间的连接上存在权值,前一层的输出信号经过处理后作为下一层的输入信号。当信号到输出层时,所输出的信号与预期输出值(非线性系数)做比较,当误差较大时,将此误差作为依据重新调整不同神经元之间的连接权值,直至输出结果达到预期精度。隐含层数目与数据之间关系的复杂程度相关,关系越复杂,隐含层数目越多。隐含层之间的交叉影响在本次实验中表示同一模型的不同出入口组合的非线性系数之间是相互影响的,并不是孤立的。
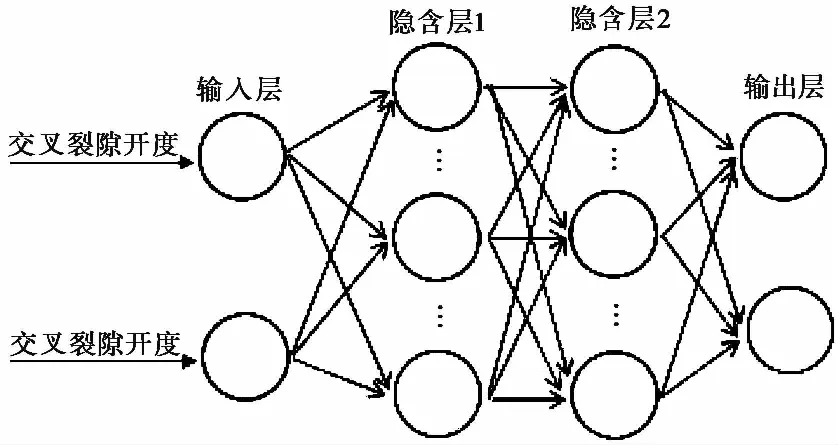
图2 人工神经网络结构示意图
2.2 训练样本获取
同一方向延伸的裂隙系统称为一个方向裂隙组。不同方向的裂隙组会彼此切割,在岩层中形成裂隙网络(田开铭,1986)。由于裂隙网络是相互切割形成的,所以岩体裂隙网络内的交叉裂隙主要是三分支与四分支交叉裂隙。本文以三分支和四分支交叉裂隙作为研究工况。同时,为了便于研究,将空间裂隙交叉点简化为二维平面交叉裂隙。在二维平面中,描述交叉裂隙的几何参数主要为裂隙分支的开度与裂隙各分支之间的角度。裂隙组交叉时,由于裂隙组方向的不确定,所以交叉裂隙之间的夹角也不确定。本文为了研究裂隙交叉角度的影响,将角度变量设置为30°、60°、90°、120°、150°、180°。李博等(2019)利用高精度三维轮廓仪对天然花岗岩裂隙表面进行扫描,采用的裂隙开度在0.5~0.75imm之间;Zhou et al.(2016)和Qian et al.(2018)在实验中开度采用0~2.0imm。相关文献中,裂隙开度大多在0.2~0.6imm之间,因此本次模型裂隙开度选用0.2imm,0.4imm,0.6imm。交叉裂隙开度非均匀性体现在两个方面:不同分支开度的非均匀性;同一分支开度的非均匀性。在本文中,对裂隙各分支设置不同的开度值,考虑了不同分支开度的非均匀性,模拟现实中的裂隙交叉点情况。由于将模型简化为二维平面,所以未考虑同一分支开度的非均匀性。
数值模拟采用有限体积法(FVM),软件选用FLUENT 6.3.26,流场计算模型选用Realizablek-ε。数值模拟工况利用典型粗糙度曲线建立。模型设置不同出入口形式(三分支为一进两出;四分支为一进三出和两进两出)、不同交叉裂隙开度和不同裂隙分支之间的角度,并进行不同组合。如,三分支工况命名为3T1E0.20.40.6A30-180(一进两出、e0=0.2imm、e1=0.4imm、e3=0.6imm、θ1=30°,θ2=180°),四分支工况的命名为4T1E0.20.4A30(一进三出、e0=e2=0.2imm、e1=e3=0.4imm、θ1=30°)。模型示意如图3所示。

图3 工况组合示意图
平面模型默认宽度为1im,边界条件设置为速度进口和压力出口。根据数值模拟的流量矢量图观察,交叉裂隙影响范围取Rr=10emax,emax为各分支的最大开度,在此范围边界取点,获得压力和流速等参数。设置数值计算残差精度为10-5。为了使出口流量不同,设置不同的出口压力。入口为流速设置,若入口分支为1个,则入口流量全从流入分支进入裂隙交叉点;若入口分支为2个,为了使工况结果具有代表性,在有限的工况数下包含尽可能多的流量组合值,将入口流速按照比值1︰4~1︰1设置。例如,在4T2E0.6A60工况中,入口流速采用0.004与0.006、0.02与0.08等组合。设置不同入口速度,计算出口流量和压差,并根据式(3)将不同流速下的出入口流量与压差值进行拟合,获得交叉裂隙非线性渗流模型中的非线性系数。数值模拟模型的网格按照最大开度的0.05倍进行设置,使网格数在100i000~250i000之间,这样划分使网格剖分能够满足计算精度,又具有较高的数值计算效率(图4)。

图4 模型网格划分图
2.3 训练样本处理
获得不同工况下的非线性系数后进行人工神经网络训练,为了提高人工神经网络预测模型的准确性,需要对输入数据进行相关处理,获得输入文本。
本文是研究开度、角度与非线性系数的关系,因此,输入文本中需要包括不同分支开度和不同裂隙出入口之间的角度。因变量的数量级较高,因此对所有的B系数降低数量级。将所有的非线性系数缩小109,将获得的数据作为输出变量。
3 研究成果
通过数值模拟获得各工况中表征交叉裂隙渗流规律的非线性系数;运用人工神经网络,获得交叉裂隙几何条件与非线性系数之间的关系。
3.1 平面交叉裂隙渗流特征
进行数值模拟及非线性参数拟合后,可以得到训练样本。为了确定所获得非线性系数的准确性,任意选取3个工况进行分析。所选取3个工况为3T1E0.2A120120、4T1E0.2A90、4T2E0.60.2A90。
将拟合得到的非线性系数带到式(3)中,得到拟合压差值,并与数值模拟结果进行对比。对比结果如图5~图7所示。可见,根据式(3)得到的非线性渗流拟合结果与模拟结果非常相近,证明了拟合得到的非线性系数的准确性,交叉裂隙渗流具有非常明显的非线性特征。

图5 3T1E0.2A120120压差与入口流量对比图像

图6 4T2E0.60.2A90压差与入口流量对比图像

图7 4T1E0.2A90压差与入口流量对比图像
观察流速矢量图发现,在低流速时,在交叉裂隙的交叉位置没有出现涡流现象(图8a),即惯性力造成的影响小,压力损失主要是黏滞力造成的,压力与流量之间具有明显的线性关系如图1所示;当流速增大时,在交叉裂隙的交叉位置出现涡流(图8b),这说明高流速下因惯性力造成的压力损失增大。这与低流速下压力损失符合立方定律,高流速下偏离立方定律的非线性特征是一致的。
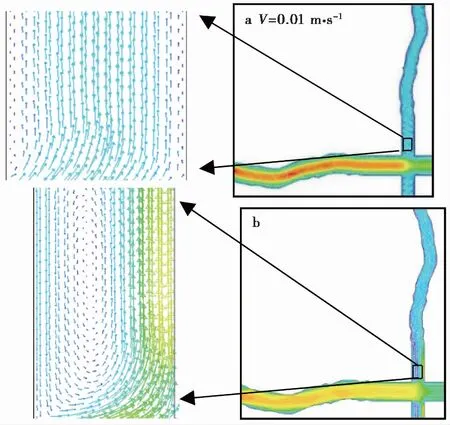
图8 e0=e2=0.6imm,e1=e3=0.4imm,θ1=90°流量矢量图
3.2 非线性参数人工神经网络预测及分析
将数值模拟获得的数据作为样本,每种情况训练出3个模型。以最佳适应值作为指标,将3个模型进行对比,获得最优模型。获得最优模型后,选定验证工况,利用最优模型对验证工况进行预测。
将预测工况几何条件输入训练的最优人工神经网络模型内,即可得到非线性系数预测值。将人工神经网络预测值与拟合非线性系数进行对比,对比结果如表1所示。

表1 非线性系数预测结果
对预测数据进行分析,三分支工况的预测值共有8个,相对误差在10%以内的7个,占87%,平均误差为5.35%。四分支一入口工况的预测值共有9个,误差在10%以内的有8个,占88.9%,平均误差为12.7%。此平均误差较大是因为其中一个预测值的偏差较大,除去此误差的平均误差为4.5%。四分支二入口共有预测值12个,其中相对误差小于10%的有10个,占83.3%,平均误差为6.8%。
综合上述分析可以得到结论:交叉裂隙几何条件与交叉裂隙渗流方程中的非线性系数存在规律,可以通过人工神经网络分析得到此规律,用于预测交叉裂隙渗流方程的非线性系数。同时,在人工神经网络模拟中,预测结果的准确性对于角度变化较为敏感,即在预测样本中开度相同,角度不同的工况预测结果较为准确。分析原因,笔者认为是由于在训练模型的输入样本中,针对同一工况的角度输入值较为完整(边界值均有且中间值较多),角度的规律较为明显、全面。开度变量由于组合较复杂,输入样本数有限,导致人工神经网络关于开度的规律不明显。
预测结果有相对误差较大的预测值出现,可能是多方面因素造成的。第一,由于人工神经网络模拟时需要训练样本数量较多,目前样本数不能对预测模型进行较为全面的训练,因此出现当预测工况自变量超出训练样本自变量范围时误差较大,可能是产生误差的主要原因。第二,数值模拟软件中的模型是基于理论建立的,模型计算与现实状态不一定完全相符。第三,模拟结果中裂隙压力等数据的提取与处理过程中存在偶然误差,很难完全避免。
4 讨 论
刘杰(2019)利用数值模拟和实验的方法对岩体裂隙网络渗流规律进行了定量探究,并得出了非线性系数计算的数值表达式。下面将从预测误差方面进行两种规律探究方法的比较。
对刘杰(2019)的误差表与本文预测误差表(表1)分析发现:利用数值表达式可以得到直观的交叉裂隙几何因素和交叉裂隙渗流模型非线性系数的关系,人工神经网络模拟的方法得到的规律不够直观。从相对误差上来说,两种方法所得到的精度差别不大,但是数值方法得到的相对误差中小于5%的比例为66.7%,而人工神经网络模拟中相对误差小于5%的比例为48.3%。因此,利用数值表达式方法得到的交叉裂隙渗流规律准确性较高。但是,数值表达式方法也有其不便之处。在大规模计算中,数值表达式应用较为困难,需要的计算量大。
同时,根据训练样本数量的不同,人工神经网络所获得的精度也不相同。训练样本数量越多,所包括的自变量范围越广,能够反映更广范围自变量范围内的裂隙交叉点渗流规律,所获得的精度也就越高。
因此,可以根据工程实践的要求来选用不同的方法:当工程处理数据量较小,且自变量范围接近时,应用数值表达式的方法,或采用较大的样本数据训练人工神经网络模型后进行预测;当工程处理数据量较大,且需要获得的数据量较大时,宜采用人工神经网络模拟的方法。
5 结 论
本文运用数值模拟及人工神经网络方法对平面交叉裂隙渗流模型非线性参数进行了研究。通过数值模拟获得交叉裂隙渗流模型非线性参数,利用人工神经网络探究交叉裂隙几何条件与交叉裂隙渗流模型非线性参数的规律,获得了以下结论:
(1)介绍了平面交叉裂隙非线性渗流模型。总结了平面交叉裂隙渗流模型非线性参数的表达方法,发现常规方法表示平面交叉裂隙渗流模型非线性参数存在适用范围小、表达式复杂等缺点,不适于工程实践的应用。
(2)提出人工神经网络预测平面交叉裂隙渗流模型非线性参数的方法。人工神经网络预测方法具有实用性强、表达方式简单、适用范围广等优点,为探究平面交叉裂隙渗流规律提供了新方法。
(3)通过预测工况验证了人工神经网络方法探究平面交叉裂隙渗流模型非线性参数的可行性,获得了较为准确的预测结果,方便进行大量数据的分析处理。
