乌梁素海湖冰晴天反照率日变化特征的统计模型比较和分析*

汤明光，李志军，卢 鹏**，曹晓卫，李国玉，Leppäranta Matti，Arvola Lauri，石利娟

(1:大连理工大学海岸和近海工程国家重点实验室，大连 116024) (2:中国科学院西北生态环境资源研究院冻土工程国家重点实验室,兰州 730000) (3:赫尔辛基大学大气与地球科学研究所，赫尔辛基 00014) (4:赫尔辛基大学拉米生物实验站,拉米 16900) (5:中国科学院遥感与数字地球研究所数字地球重点实验室，北京 100094)

反照率是物质表面的固有光学特性. 地表由多种物质组成，而物质表面反照率随其成分及结构、光线入射角和周边环境变化存在时空差异，所以地表反照率实际上是随经纬度、儒历日和云量变化的动态参数. 反照率的细微变化会影响到地气系统的能量收支平衡. 在全球气候变化日益突出的背景下，反照率成为地球科学研究领域的热点问题. 其中，冰面反照率不仅应用到各种光学遥感遥测技术、航空拍摄和高光谱成像监测、以及气候变化中的大气-陆面能量平衡研究，而且对于海冰、湖冰、河冰而言，它还能够成为冰下水生化环境和生态响应的驱动因子. 一般而言，冻结的冰面能够引起反照率增大、蒸发降低和进入水体的太阳辐射降低. 这些过程会造成大气和湖泊之间动量和能量交换减弱，湖泊水体内部的湍流混合过程减弱，进一步引发冰下水体温度、溶解氧、叶绿素等生化环境条件的变化[1-2].

中国冰下水环境研究相对集中在内蒙古乌梁素海，开展的系列工作包括水质现场调查[3-4]、实验室测试[5]、冰-水-泥物质交换[6]. 这些成果尚未明确解释冬季湖泊结冰后水生化环境要素变化的驱动力. 而国际研究成果则表明太阳辐射是冰下水生化环境要素变化的关键因子. 首先太阳辐射能量驱动冰下水体对流[1]，使其具有显著的日变化[7]和季节变化[8]. 之后水动力同生化过程联合作用引起溶解氧[2]、浮游生物[9-10]的规律性交换运动. 但已有成果只是具体到某一冰下水物理和生化因素变化之间的关系，缺乏同太阳辐射、气象要素(云量、气温、风)和冰物理要素(冰厚、晶体结构、冰内气泡)之间的联系. 其必要性是因为：首先冰的生消是气象要素控制的能量和质量平衡的结果；其次冰晶体和冰内气泡等物理要素决定着冰的消光系数. 而消光系数一定时，传递到冰下的辐射能量又随着冰厚的增加而减少. 因此，理解冰下水生化环境变化的太阳辐射驱动力，需要将冰面气象要素、冰光学参数和冰物理参数联合起来形成一个耦合体系.

冰面反照率是气-冰-水-生态耦合系统的关键输入变量之一. 但计算冰面反照率日变化没有统一的表达式，也没有规定的观测数据拟合方法. 不同学者根据自己的研究目标决定数据处理方式，具体到湖冰反照率日变化的参数化更是罕见. 光学卫星遥感则需要能够反映过境时刻的下垫面反照率. 在陆面能量平衡和植物生长计算中，太阳高度角小于15°时的辐射通量约为每日太阳辐射总量的10%，而太阳高度角小于5°时的辐射通量则仅为日总量的1%. 因此当太阳高度角小于一定值时，其辐射能量就可以忽略. 在选择反照率日变化观测数据分析的始终点时，有以太阳高度角做判据的，选择的起始太阳高度角为5°[11]、15°[12]、30°[13]，甚至40°[14]；有以辐射通量做判据的，分别是5 W/m2[15]、30 W/m2 [16]、50 W/m2 [17]、100 W/m2 [14]；或者规定冬季和春季分别采用8:00-18:00[17]或者6:00-19:00[14]时间段的辐射观测数据.

利用Trios高光谱辐射传感器能获得太阳高度角从黄昏到晚霞时段的每分钟可靠辐射记录数据，计算出稳定的湖冰反照率[15]. 从物理角度看，太阳高度角从日出的0°到日落的0°之间的反照率曲线具有双峰特征. 以往反照率观测技术灵敏度低[16,18]、记录频次少，观测数据难以获得这种曲线. 即使考虑早晚地面太阳总辐射较小，并存在散射[16-17]等影响，当反照率日变化的时间范围覆盖太阳高度角大于5°的时段，曲线仍然呈双峰. 但如果覆盖的时间范围是太阳高度角大于15°对应的时段，则曲线处于两个峰值之间，呈U型[16]. 对于U型变化，文献认为反照率和太阳高度角之间呈指数函数关系[12,14]，但只能将U型分为前后2段，分别计算. 由于指数函数不存在峰值，如果统计式不指明适用范围，当计算到接近日出和日落时刻，计算值就高于实际值. 为了体现峰值，有学者采用3次幂函数拟合，而其后半段在计算中排除[19]. 事实上，有不少密度分布函数在形式上保持指数函数形式，并且具有两侧对称或不对称的峰值，只是计算相对指数函数繁琐. 如果利用这些密度分布函数，既保留反照率随太阳高度角呈指数函数形式变化的普遍作法，又能描述出峰值，建立普适性表达式. 因此本文首先利用在乌梁素海观测数据给出湖冰反照率日变化特征，其次对比与前人观测结果的差异和原因，最后寻找采用概率密度分布函数建立湖冰反照率日变化的普适性数学表达式，实现利用一个表达式既能计算太阳高度角大于5°时间范围的双峰反照率日变化曲线，也能计算太阳高度角大于15°时间范围的双峰之间U型反照率日变化曲线.

1 观测地点和方法

1.1 观测地点

依托内蒙古乌梁素海湿地生态系统国家定位观测研究站，开展了4个冬季的气-冰-水-泥物理与水生态综合调查研究. 乌梁素海属于中国西北半干旱地区的多功能型湖泊，是中国八大淡水湖泊之一，面积约300 km2，地处北纬41°N、东经108°E，海拔高度1020 m. 湖泊周边为农田、沙漠和盐碱地，岸边生长着茂密的芦苇. 该湖泊每年冬季都会结冰，冰厚60～70 cm. 冰面基本平整，只存在个别隆起冰脊. 有些冬季冰面存在积雪，在大风天气会将周边农田沙尘带到冰面或雪面. 该湖冬季晴天日数多于阴天和多云天气总数，每日有8小时以上的日照，但最大太阳高度角仅接近35°. 本文基于2019年1月16日至2月11日在湖的中东部开展的湖冰反照率调查研究，观测点为离岸边芦苇约1 km的开阔冰面，其表面只有5 mm厚度的零星积雪斑块，冰内存在明显的气泡，测试期间没有降雪. 乌梁素海的详细自然环境条件参考文献[3-4].

图1 乌梁素海冰面辐射观测的照片Fig.1 Photos of radiation observation over the Lake Ulansuhai ice surface

表1 Trios光谱传感器技术参数

1.2 观测方法

观测时将两个Trios高光谱辐射传感器固定在距冰面1 m高度，分别竖直朝上和朝下(图1)，其中朝下的传感器在冰面投影点20 m半径范围内为裸冰，其他部位的积雪斑块对反射光谱无影响. 每分钟记录1次入射和反射光谱. 此外，有4个辐射传感器安装在冰下不同深度. 现场观测工作持续25天.

该辐射传感器的有效测量波长范围为320～950 nm，分为190个波段，对应的采样间隔约为3.3 nm(±0.3 nm)[15]. 具体传感器技术参数汇总见表1. 该传感器的精度能够满足包含散射辐射通量时的反照率计算精度要求.

2 湖冰反照率的日变化特征

将辐射传感器测量的入射辐射和反射辐射进行积分，得到光谱的积分通量. 之后利用反射辐射通量与入射辐射通量之比获得冰面反照率. 观测期间晴天有15天，少云、多云和阴天共计10天. 分析每天反照率的日变化曲线，发现湖冰反照率从日出到日落的变化同云量有很大关系. 图2绘制了5种不同天气的反照率日变化典型曲线. 其中，2019年1月22日为晴天的变化曲线. 该日各时刻太阳的入射和反射强度、反照率不属于最强，曲线上噪音信号较小，上午和下午各有一个峰值. 第一峰值出现时刻大约为日出后1.5 h，对应太阳高度角为13.12°～14.39°；第二峰值大约出现在日落之前0.8 h，对应太阳高度角为4.81°～8.87°. 两个峰值的反照率不等，表现出明显的不对称[20]. 晴天反照率谷值出现时刻约为日长的一半，对应太阳高度角范围在28.69°～32.48°之间. 但是因北京与地方午时的差异，反照率谷值出现在一个时间区域，也导致双峰左右两侧的时间范围不对称. 为了同反照率日变化的U型曲线对比，这种双峰曲线本文简称为偏M型.

2019年1月18日为多云天气，该日的反照率对比晴天有一定的减弱，反照率曲线仍然呈偏M型，但是噪音增强，表现出云量和位置变化带来的影响. 另外，第一峰值相对晴天延迟出现0.5 h，而第二峰值提早出现2.0 h(见图2中的红线). 如果上午为阴天时，第一峰值不明显(图2中2019年1月28日)；而下午为多云时，第二峰值偏低(图2中2019年1月17日). 阴天的冰面反照率日变化曲线仍然保持双峰特征，两个峰值基本对称. 第一峰值出现比晴天约晚0.5 h，第二峰值比晴天提前1.5 h. 但反照率峰值明显小于晴天. 全天接近常数(图2中2019年1月30日)，但比黄昏时的稍高，属于相同量级.

5种不同天气的反照率日变化主要来自云量的影响，而云量对太阳辐射的影响可见图3[21]. 当太阳高度角相同时，云量越高，到达冰面的太阳辐射强度越低，两者具有明显的非线性关系. 当云量占比大于80%时，它对到达冰面的太阳辐射通量影响最显著. 可见，一般用于天气描述的“晴天、少云、多云、阴天”等概念显然不适用于开展图2所示的反照率定量分析. 因此，目前的研究只能对云量为0的晴天和云量100%的阴天开展定量分析. 而阴天对应的反照率基本为一常数. 另外，前人采用总辐射量30 W/m2[16]、50 W/m2 [17]和100 W/m2[14]作为分析反照率日变化的阈值，也只能针对晴天，对阴天并不合适.

图2 不同天气情况的冰面反照率日变化Fig.2 Diurnal variation of ice albedo under different sky conditions

图3 日平均总云量与太阳总辐射相关性[20]Fig.3 Correlation between diurnal averaged total cloud fraction and total solar radiation[20]

2019年1月22日的晴天观测数据可以同文献资料进行对比. 由于文献中一般只给出地方中午前后的测量结果，对该日从日出至日落和北京时11:00-14:00间的观测数据，分别计算反照率算术平均值和入射强度加权平均值. 采用日出至日落反照率计算的算数平均值和入射强度加权平均值，分别为0.3242和0.3197，采用11:00-14:00的2种均值，分别为0.2849和0.2847. 这说明峰值参与平均计算的结果偏大. 11:00-14:00之间Bolsenga[11]测试了300～3000 nm波段的反照率后指出纯净湖冰的反照率为0.10，含气泡湖冰的反照率为0.22. 章睿等[22]报道北极海冰中的反照率：白冰为0.54，蓝冰为0.31，灰冰为0.21. 乌梁素海湖冰内的气泡明显，反照率会偏高，但是目前没有关于气泡含量及尺寸对反照率效应的研究. 全天阴时的冰面反照率比晴天小，4种平均方法均接近0.25. 2种全天多云和下午多云的地方午时前后平均反照率与晴天接近. 下午多云地方午时前后的平均反照率与全天阴的接近. 5种典型天气的反照率平均值见表2.

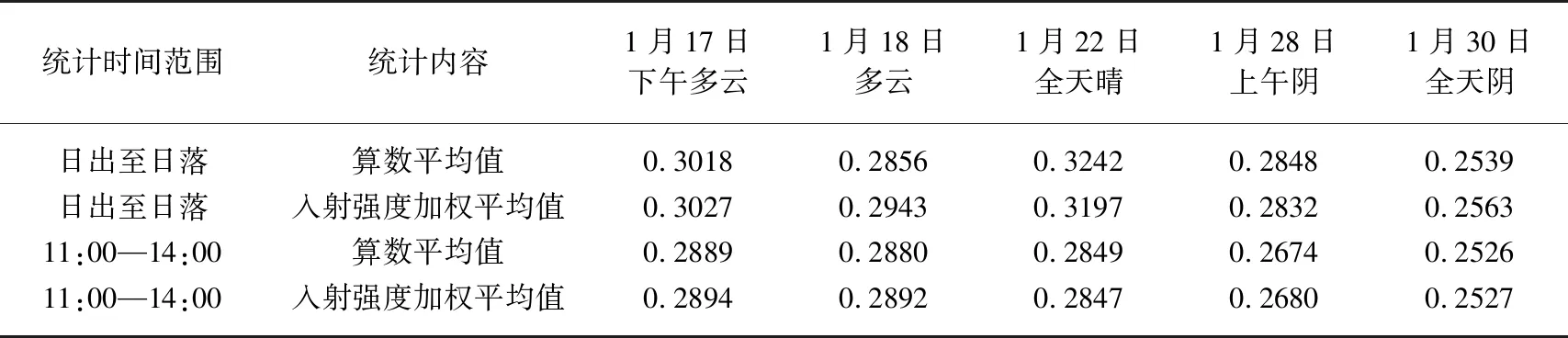
表2 不同天气不同时间范围的反照率算数平均值和入射强度加权平均值

3 数学统计模型的构建、拟合和选取

3.1 构建数学统计模型的思想

表面反照率参数化方案需要考虑太阳高度角和表面特征两个独立的影响因素，两者之间对反照率的贡献构成乘法或者加法关系[23]，但参数的基本形式应该符合反照率变化的基本特征. 这就表明仅用某一固定的算法并不适宜，可以根据现场研究成果的积累而逐渐完善. 乌梁素海晴天湖冰反照率的完整日变化曲线具有双峰特征，忽略夜间数据，将反照率日变化视作周期变化，统计模型时间单位采用日. 应用线性叠加原则，用2个密度分布函数错峰叠加，就可以形成具有双峰的函数形式，而且2个峰值独立存在，能表达出其不对称性[20]. 新统计模式为了兼顾不同研究目标所需的不同统计时间范围，要求模型表达式即能计算具有双峰特征呈偏M型的日变化曲线，也能计算太阳高度角大于一定阈值后，双峰之间呈U型的日变化曲线. 避免将U型曲线分为二段指数函数来表达，从而保持模型的简洁.

考虑早晚太阳入射辐射较小，并存在散射[16-17]影响，以太阳高度角5°为阈值[11]，将乌梁素海日出时(太阳高度角等于0°)设为C点，日落时(太阳高度角等于0°)设为D点，选取晴天观测数据中太阳高度角大于5°的数据进行统计. 每日D点和C点间的时段作为密度分布函数的基本尺度参数. 2个峰值的实际尺度参数设为尺度参数变形系数(g1和g2)与基本尺度参数之积, 即g1(D-C)和g2(D-C). 拟合峰值出现时刻作为密度分布函数的位置参数(μ1和μ2). 根据上述思想，选择常用的拉普拉斯、高斯、耿贝尔、柯西密度分布函数进行组合. 形成4种组合统计模型，分别简称拉普拉斯组合、高斯组合、耿贝尔组合和柯西组合，见公式(1)～(4). 之后拟合湖冰观测数据，对比拟合结果来确定最佳统计模型.

拉普拉斯密度分布函数组合：

(1)

高斯密度分布函数组合：

(2)

耿贝尔密度分布函数组合：

(3)

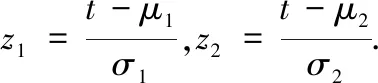
柯西密度分布函数组合：

(4)

式中，a为综合拟合系数，下角标1、2分别代表第一峰值和第二峰值；t为一日中的时刻，单位d；σ1、σ2分别为拟合第一峰值和第二峰值对应的实际尺度参数. 因此，引入尺度参数变形系数，这时：

σ1=g1(D-C)

(5)

g1=L1·C2+M1·C+N1

(6)

σ2=g2(D-C)

(7)

g2=L2·C2+M2·C+N2

(8)

式中,L、M、N分别为式(6)和式(8)的统计系数，下角标1、2分别代表第一峰值和第二峰值；g1为第一峰值尺度参数变形系数;g2为第二峰值尺度参数变形系数;C为日出太阳高度角0°对应时刻；D为日落太阳高度角0°对应时刻；D-C为基本尺度参数.C和D根据当地经纬度和儒历日，由理论计算. 理论公式的简便计算方法见文献[24]，此处不再累赘. 4种组合统计模型的尺度参数变形

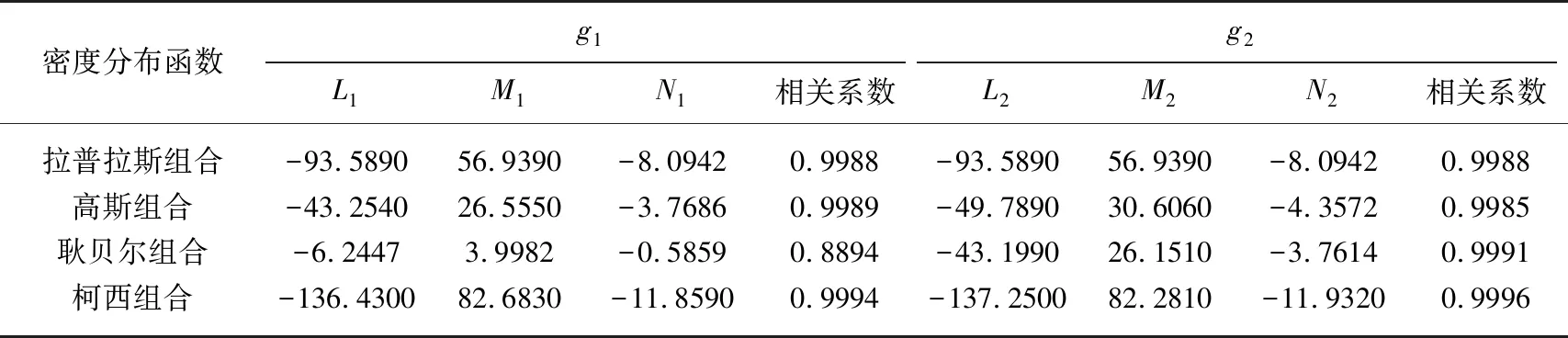
表3 尺度参数变形系数与日出时刻拟合关系系数

系数与日出时刻具有抛物线型关系，具体统计系数和相关系数汇总在表3. 表3中的相关系数量级相同，统计系数之间的比例基本相同. 耿贝尔组合的第一峰值和第二峰值的尺度参数差异较大，拉普拉斯组合的2个峰值的尺度参数相同，另外2种组合统计模型的尺度参数接近. 从发展参数化方案角度出发，尺度参数相同的拉普拉斯组合可以简化计算步骤.

利用乌梁素海观测点的经纬度计算每天日出和日落时刻，并提取观测期间每一天的反照率日变化曲线的峰值点时刻. 发现第一峰值和第二峰值的位置参数也与当地日出时刻有关，即与地理位置和儒历日有关. 乌梁素海的位置参数拟合为线性关系:

μ1=0.8973C+0.0955

(9)

μ2=-0.6237C+0.9073

(10)

式中，μ1、μ2分别为第一峰值和第二峰值的位置参数；C为日出时刻.

3.2 组合统计模型拟合方法和结果

组合统计模型需要确定6个统计参数，其中4个均与当地经纬度和儒历日有关. 因此，拟合需要首先由后向前逐步确定出这4个参数，之后再由组合模式计算日变化. 具体步骤是：1)利用每日的峰值出现时刻和日出时刻，拟合式(9)和式(10)，得到2个峰值的位置参数μ1和μ2. 2)将μ1和μ2作为已知参数赋入选定的组合统计模型，即式(1)～式(4)的某一个. 利用Origin软件进行多参数拟合，得到初选尺度参数σ′1和σ′2，综合系数a′1和a′2. 对于拉普拉斯分布函数组合，拟合中发现σ′1和σ′2接近但不相等，为方便计算且符合物理意义，因此取它们的平均值为初选尺度参数, 令σ′1=σ′2. 3)利用初选尺度参数σ′1和σ′2分别拟合尺度参数与日出时刻C和日长(D-C)的非线性关系，即使用式(6)、式(5)或式(8)、式(7)，得到尺度参数σ1和σ2. 4)将μ1、μ2、σ1、σ2

表4 2019年1月29日太阳高度角≥5°时间范围的 4种组合统计模型拟合相关分析

再次赋入组合统计模型，利用Origin软件进行多参数拟合，得到综合系数a1和a2.

采用4种组合统计模型分别拟合2019年1月29日日出至日落前太阳高度角≥5°的反照率观测值，得到该日的拟合曲线，结果见图4a. 图4b直观给出4种组合统计模型拟合反照率与现场观测反照率的统计关系，其对应的拟合相关系数、均方根误差和绝对平均误差见表4.

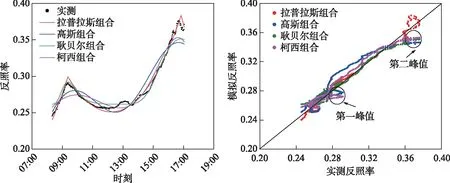
图4 2019年1月29日太阳高度角≥5°时间范围的4种组合统计模型拟合曲线和拟合效果对比： (a) 组合统计模型拟合的反照率日变化曲线，(b) 实测和组合统计模型拟合反照率对比Fig.4 Comparison of the fitted results for the measured albedo over 5° solar elevation angle on 29 January, 2019 by using the four combined statistical models

图4a反映出柯西组合对2个峰值的拟合偏低，而且在低太阳角时，拟合结果均偏低. 在正午前后太阳高度角较高时，拟合结果均偏大. 另外拟合曲线的峰值两侧比较缓，导致拟合的第一峰值比实际偏后出现，而拟合的第二峰值比实际提前出现. 高斯组合对于峰值部位的拟合比柯西组合稍高，但仍然低估很多. 对于早晚的反照率显得偏离大. 峰值的位置同样是相对第一峰值的位置偏晚，相对第二峰值位置偏早. 曲线的谷值也低估. 只是在双峰之间反照率曲线下降和上升阶段拟合的最佳. 因此该组合适合太阳高度角大于15°的U型反照率日变化曲线的拟合，不适合太阳高度角大于5°的偏M型反照率日变化曲线的拟合. 耿贝尔组合对第一个峰值在反照率和峰值位置方面拟合均好，但对第二个峰值拟合相对较差. 拟合的第二峰值在反照率上偏低，在峰值位置上偏早. 拟合的午时前后部分非常平坦，并且拟合的反照率偏高. 耿贝尔组合在计算上又比其他组合多1个计算步骤. 拉普拉斯组合拟合最好. 它的峰值比较尖，对第一峰值和第二峰值的反照率拟合的稍高，对2个峰值的位置拟合最佳. 午时前后光滑过度，只是比实测值拟合较低. 另外，根据其他3种组合在单峰及谷值的拟合曲线特点，也没有必要选择不同密度分布函数进行线性组合.

图4b给出2019年1月9日4种组合统计模型拟合结果与观测结果的关系. 图中的实测反照率数据518个，它们的变化范围在0.25～0.38之间. 其中2个圆圈的位置为第一峰值和第二峰值对应的高斯组合、耿贝尔组合和柯西组合的拟合结果，它们均小于观测结果. 唯有拉普拉斯组合在实测范围内表现良好. 表4的相关系数均大于0.9517，均方根误差小于0.0108，平均绝对误差小于0.0089. 这说明仅从表4数据量级上不能直接剔除哪种组合不可信，但相关系数和误差的微小差别仍然反映拉普拉斯组合效果最佳.

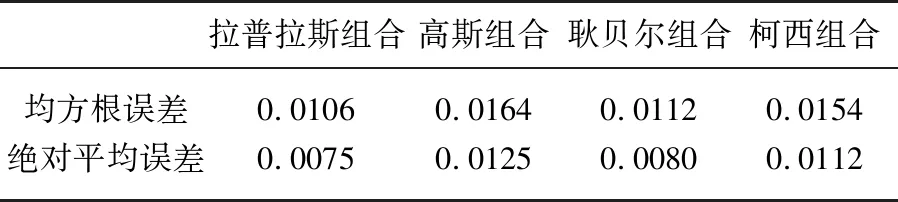
表5 2019年1月-2月12天太阳高度角≥5° 时间范围反照率的4种组合统计模型拟合误差分析

整个调查期间12个晴天的太阳高度角≥5°的反照率数据6231个，将它们做与图4b相同的分析，得到4种组合统计模型拟合结果与观测结果的关系(图5). 图5直观地表明拉普拉斯组合统计模型的数据散点分布均衡，而其他3种组合都明显存在拟合峰值偏小所带来的明显偏差. 表5的误差分析数据又进一步证实拉普拉斯组合的误差小于0.0108，是最佳组合统计模型. 在此基础上，图6给出2019年1月-2月12条晴天反照率日变化的拉普拉斯组合统计模型拟合曲线. 它更直观地表现拉普拉斯组合统计模型的效果. 表6所给的逐日拉普拉斯组合统计模型拟合相关系数、均方根误差和平均绝对误差显示了每一日结果的可靠性. 12天当中，最大误差为0.016. 此外，表6还给出了拟合的拉普拉斯组合统计模型综合系数a1和a2.

图5 2019年1-2月12个晴天太阳高度角≥5°时间范围反照率的4种组合统计模型拟合效果对比Fig.5 Comparison of the fitted results for the 12 days measured albedo over 5° solar elevation angle in January-February, 2019 by using the four combined statistical models

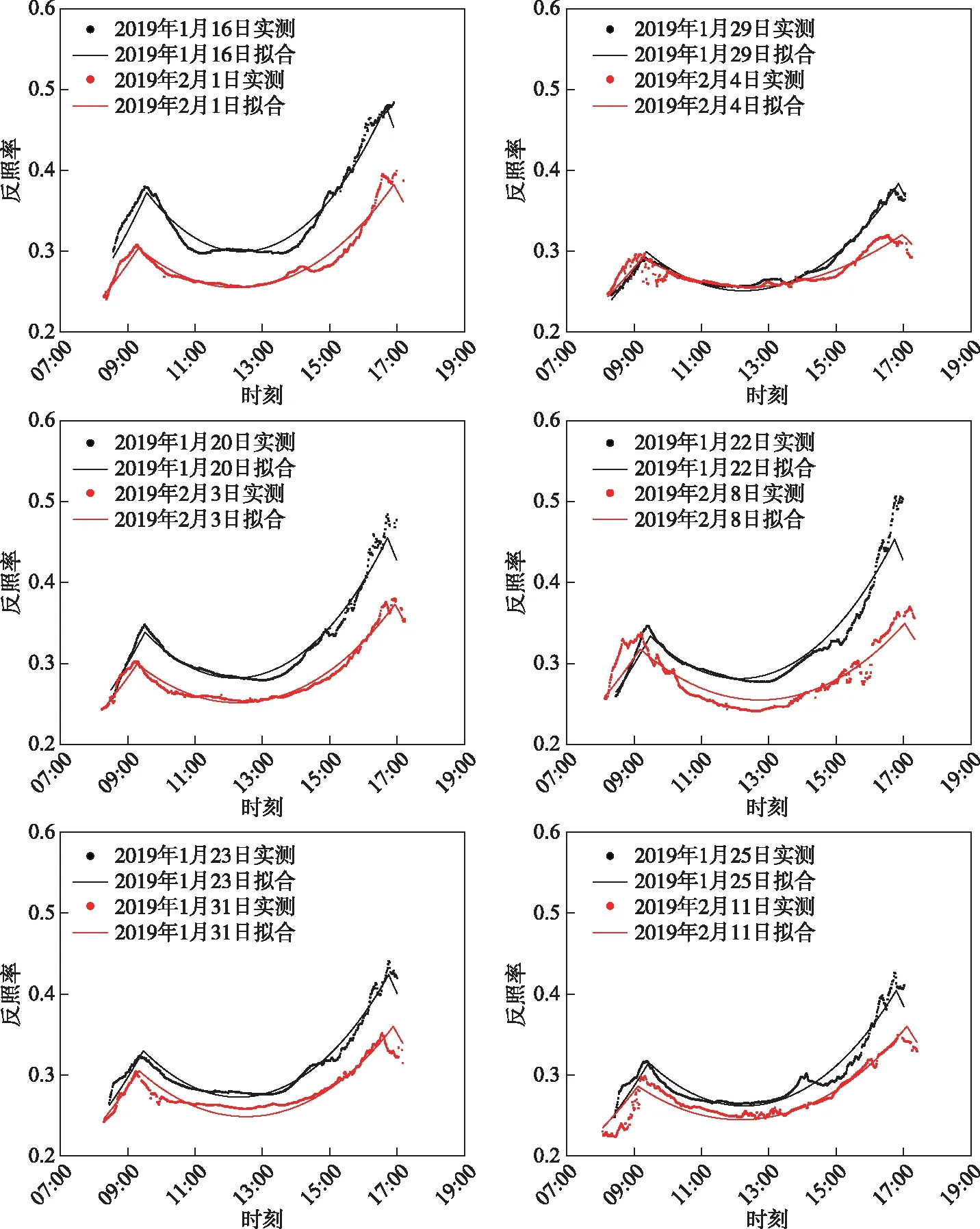
图6 2019年1-2月12个晴天太阳高度角>5°反照率的拉普拉斯组合拟合曲线Fig.6 Fitted curves for the 12 days measured albedo over 5° solar elevation angle in January-February, 2019 by using Laplace combined statistical model

从表6中的综合系数看，它们有一定的变化. 这2个系数决定反照率的整体高低，它们的差异说明湖冰表面反照率日变化除了太阳辐射角和云量影响外，还会有其他次要因素. 理论上，气象因素(云[19]和温度[25])以及冰物理因素(冰厚度、冰面粗糙度和沙尘等污物)均包含在拉普拉斯组合统计模式的综合系数a1和a2中. 表6中a1的最大值和最小值分别为0.0709和0.1088，均值为0.0944，均方差为0.0071.a2的最大值和最小值分别为0.1232和0.1816，均值为0.1397，均方差为0.0151. 如果a1和a2均值减或加3倍均方差，所得结果分别接近a1和a2的最小值和最大值. 将a1和a2的均值减3倍均方差、均值、均值加3倍均方差分别代入式(1)～(4)的12天拟合公式中来代替a1和a2进行计算. 发现12天均使用均值，一日内反照率的差异小于5%. 但采用减或加3倍均方差计算，可产生16%的差异. 因此，如果不考虑次要影响因素，采用拉普拉斯组合统计模型的平均综合系数直接建立冰面反照率日变化模型，会构成大约±0.01的绝对误差.

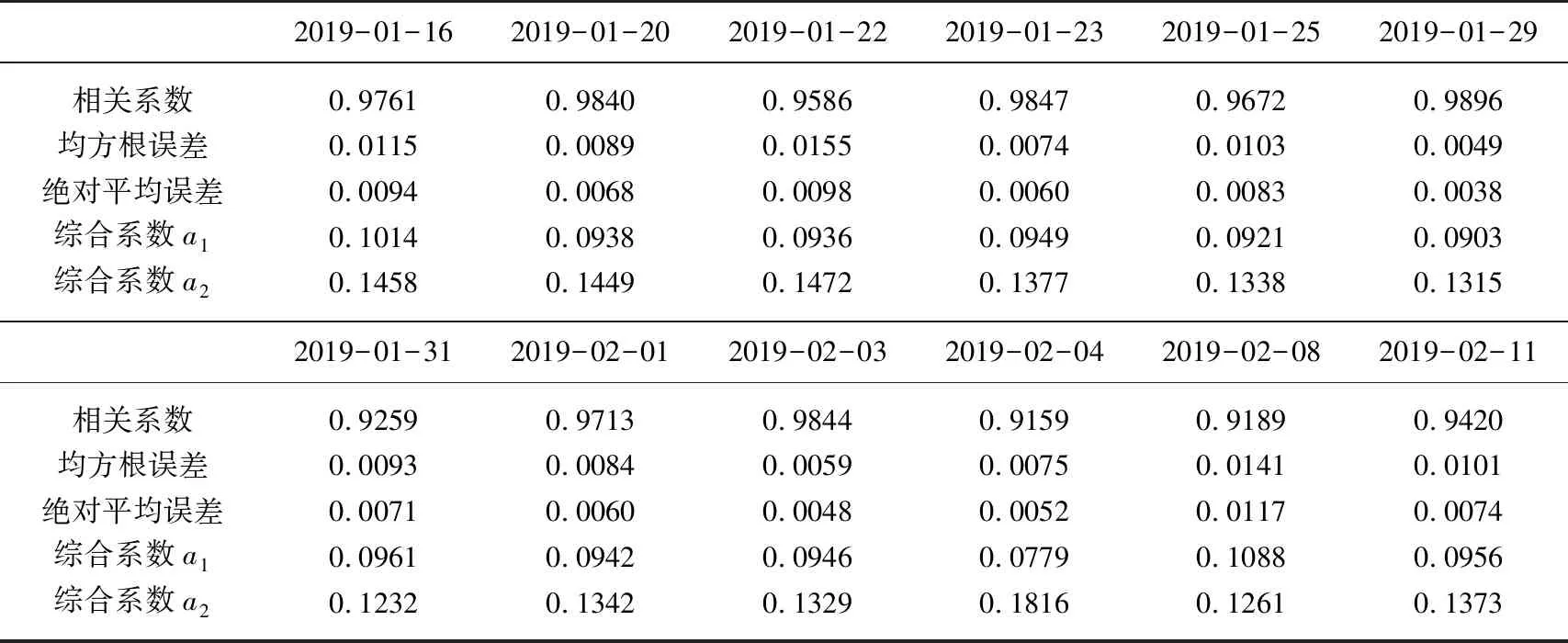
表6 拉普拉斯组合拟合2019年1-2月12个晴天太阳高度角>5°反照率日变化的相关系数、误差和综合拟合系数a1和a2

我国北方大部分地区属于干旱和半干旱，内陆湖泊、河流冰面会存在沙尘. 沙尘越多反照率越低[26]，冰川冰[12,25]和海冰[27]都有报道. 从理论研究出发，随着对湖冰反照率机理认识的提高，应该逐步从综合系数中定量分离出其他气象、冰物理、大气沉降物的贡献. 另外，乌梁素海冬季日内最大太阳高度角是35°，统计模式对于太阳高度角超出35°时，本文统计方式的适用性需要现场验证. 但是目前的数学模型，结合冰面总辐射，可以为驱动冰下水体辐射能量，进而驱动冰下水生态系统变化提供输入. 也能为内蒙古“一湖两海”、青藏高原黄河源的冰下水体水环境和生态研究及应用提供支持.

4 结论

1) 利用Trios高光谱辐射传感器实现每分钟1次辐射数据采集，能够获得从日出到日落的高精度辐射通量，计算得到表面反照率. 乌梁素海湖冰晴天反照率日变化表现出日出后和日落前各有一峰值，峰值出现时刻与日出时刻有关. 2个峰值不等，具有明显不对称性. 少云天的反照率日变化仍保留双峰特征，但曲线具有噪音信号，并且第一峰值出现时刻相对延迟，第二峰值出现时刻则提前. 多云到阴天情况下的反照率偏低，根据多云和阴出现时间，可以缺失第一峰值或者第二峰值. 全阴天的反照率基本保持稳定不变.

2)提出的4种概率密度分布函数组合统计模式，均能模拟具有双峰特征和双峰之间呈U型的反照率日变化曲线. 模型中的峰值位置、基本尺度和尺度参数变形系数与当地日出时刻关系密切，进而解决了北京时和地方时的差异问题. 利用太阳高度角≥5°反照率实测数据拟合，发现拉普拉斯组合统计模型在模型形式、统计参数、绝对误差均为最佳.

3)如果将拉普拉斯组合统计模型的综合系数取12个晴天的平均值，计算得到的反照率与观测值相比的误差不超过5%，因此可以作为湖冰反照率的参数化方案. 但从物理机制上讲，云、气温、冰面积雪、冰面沙尘量以及结冰初期和融冰后期冰面水分等次要影响因素均体现在组合统计模型的综合系数中，它们的定量化工作还需在未来调查研究成果中积累数据和继续深入.

致谢：感谢内蒙古乌梁素海湿地生态系统国家定位观测研究站提供的现场工作条件和参加野外工作的王庆凯、于淼、祖永恒、王绍宇等同学的辛勤劳动. 在论文写作过程中得到南京信息工程大学蒋熹、西北大学王宁练、中国科学院遥感与数字地球研究所邱玉宝、陈甫、浙江师范大学林兴辉、芬兰气象研究所程斌的有益建议和讨论，在此一并致谢.