火箭发动机涡轮典型结构形式对叶片低周疲劳寿命的影响研究
2020-10-29姜金朋刘志超
姜金朋, 刘志超,刘 筑, 巩 帆, 王 珏
(1. 中国运载火箭技术研究院空间物理重点实验室,北京 100076; 2. 中国运载火箭技术研究院,北京 100076)
0 引言
随着太空探索和开发利用的不断深入,火箭发动机性能不断提高,对于重复使用火箭发动机而言,高压涡轮泵是发动机中使用寿命最低的部件[1],而涡轮叶片是限制发动机寿命的瓶颈[2],因此,火箭发动机重复使用必然对涡轮寿命和可靠性提出更高的要求。
航空发动机涡轮叶片寿命研究较广泛[3-6],由于燃气温度高,工作时间长,通常需要考虑蠕变。液体火箭发动机涡轮叶片疲劳寿命的研究相对较少,航天飞机主发动机SSME研制过程中发现,引起涡轮叶片根部位置疲劳裂纹的主要因素是点火和关机过程的瞬态热应力[7]。火箭发动机涡轮工作时间短,特别是对于燃气温度不高的涡轮,可以不考虑蠕变损伤[8]。为提高SSME涡轮叶片热疲劳寿命,研究者从载荷、材料、几何方面进行了分析,并认为通过改变叶片设计提高低周疲劳寿命是最好的思路[9]。Porreca等[10]采用耦合传热方法与有限元法,研究叶冠结构对涡轮气动性能、热载和寿命的影响,结果表明,通过对部分叶冠进行较小改进,可以改善气动性能和叶片寿命。
带冠(围带)叶片可以减小涡轮中的二次损失,提高涡轮效率,但也增加了叶片的应力[11-12],叶片顶部尾缘和前缘应力集中,都可能成为失效发生的危险点。叶片空心结构可以降低叶片热应力,还能减轻涡轮质量,对于不带冠涡轮来说,可能是一种理想的结构方案。因此,本文通过热结构分析和低周疲劳损伤分析,研究带冠、不带冠、部分冠和空心对叶片寿命的影响。
1 模型及边界条件
1.1 计算方法
1.1.1 热分析方法
非稳态导热问题应满足如下形式的能量守恒方程
(1)
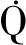

(2)
式中,λ为导热系数。结合以上两式,无内热源的涡轮非稳态导热问题的求解,最终归结为在一定的初始条件和边界条件下求解以下导热偏微分方程
(3)
假设涡轮初始温度均匀为T0,则给定如下初始条件
T(x,0)=T0
(4)
对于与燃气接触的各表面,给定对流换热边界条件如下
(5)
式中,n为换热表面的外法线,h为对流换热系数,Tw为未知待求解的结构表面温度,Tg为靠近壁面的燃气主流温度。
对于未与燃气接触的涡轮盘其他外表面,假设为绝热边界条件
q·n=0
(6)
1.1.2 结构分析方法
本文采用Chaboche随动硬化[13]与非线性等向硬化相结合的模型进行结构分析。Chaboche随动硬化模型基于Von Mises屈服准则,屈服函数如下
(7)
式中,σ为应力张量,α为背应力张量;s为偏应力张量,a为偏背应力张量;R代表屈服面尺寸,在随动硬化模型中(不考虑等向硬化时),R为常数。
流动准则描述塑性流动方向,塑性应变在屈服面梯度方向增加
(8)
式中,dεp为塑性应变增量,λ为塑性乘子。
Chaboche硬化模型是几个Armstrong硬化模型的叠加,表达式如下
(9)
式中,M为叠加的随动硬化模型数目,随动硬化分量(背应力分量的演化)定义如下
(10)
式中,Ci和γi为材料参数,dp为累积塑性应变,定义如下
(11)
等向硬化律通过以下方程描述
dR=b(Q-R)dp
(12)
式中,Q和b是等向硬化材料参数。
通过优化得到的GH4169材料参数如表1所示。

表1 GH4169材料参数
采用Manson-Coffin理论预测低周疲劳损伤,并考虑主应力的影响,进行SWT修正,得到应变-寿命公式如下[14]
(13)
式中,Δε为应变幅值,NL为低周疲劳寿命循环次数;E为材料的弹性模量,σ′f,ε′f,b,c是材料的疲劳性能参数,对于GH4169合金,其值分别取为1 546 MPa,0.412,-0.07,-0.73[15]。
注1 一、二阶异构多智能体系统一般包含多个一阶系统和多个二阶系统,而本文中系统式 (1) 与此略有差异,因此也可称系统式 (1) 为“伪异构系统”,即异构系统的特殊化处理.
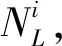
(14)
根据Palmgren-Miner线性累积损伤法则,当累积损失达到1时结构发生破坏,此时疲劳寿命为Nt,即
(15)
采用疲劳寿命分散系数评估结构的安全寿命,本文中取疲劳寿命分散系数为4[17]。
1.2 计算模型
以某液体火箭发动机涡轮(如图1(a)所示)叶片为研究对象,开展热结构和动力响应分析。涡轮将高温高压气体的能量转变为转轴的动能,因此涡轮叶片承受热载荷、气动载荷及离心载荷等,热载荷由高温燃气引起,特别是发动机启动关机瞬间,温度梯度和变化率高,热冲击影响大;离心载荷由涡轮高速转动引起。考虑到涡轮周向的循环对称性,取一个叶片进行仿真计算,计算模型如图1(a)所示。对轮毂中心线上的节点施加径向约束,约束中心线下游端面中心轴半径范围内节点的轴向位移;对叶冠和轮毂周向面上的节点施加耦合约束,得到循环对称边界,约束轮盘突台周向面上节点的周向位移;热载荷和气动载荷施加到所有与燃气接触的面,包括叶冠表面、叶片表面及轮毂上表面。热分析采用单元类型为Solid 90,结构分析单元类型为Solid 186。在带冠涡轮基础上,保持叶型不变,进行适当修改,得到不带冠涡轮(图1(b))、带部分冠涡轮(图1(c))和空心叶片模型(图1(d))。部分冠涡轮的叶冠前端面距叶片前缘和后端面距叶片尾缘的轴向距离为11 mm;空心叶片的孔形状与叶型相似,叶片近似为薄壁结构,叶片顶部壁厚约1.5 mm,根部壁厚约2.5 mm,不同结构约束及载荷施加与带冠涡轮叶片相近。

(a) 带冠涡轮模型

(b) 不带冠涡轮模型
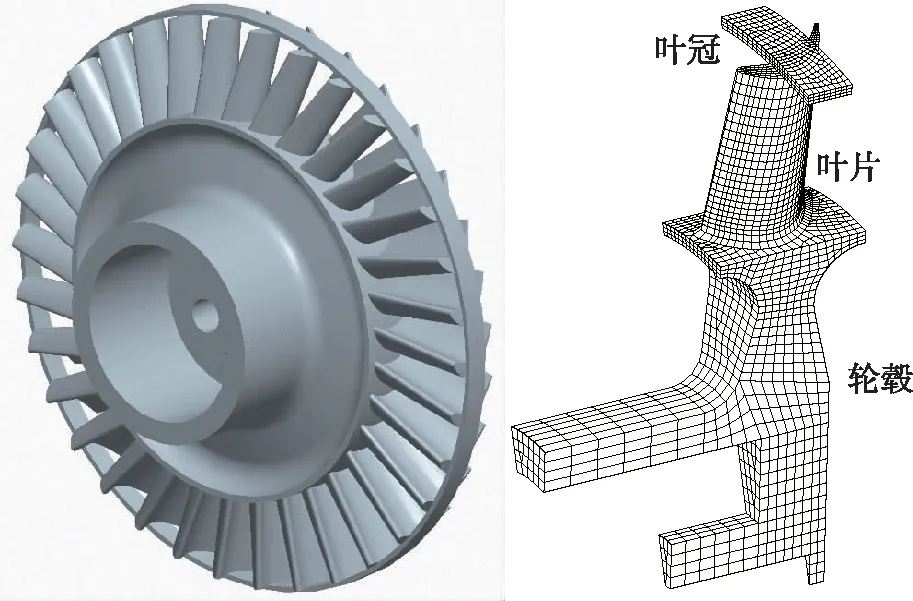
(c) 带部分冠涡轮模型

(d) 空心叶片模型图1 不同结构形式涡轮叶片模型Fig.1 Models of turbines with different structure
1.3 边界条件
考虑热载荷及离心载荷,进行热结构分析,加载分为4个阶段:启动阶段S1、稳定工作阶段S2、关机阶段S3和后冷阶段S4,各阶段时长如表2所示。一个周期内,涡轮进出口参数及转速变化如所示图2。稳定工作阶段,涡轮入口总压47.5 MPa,总温771 K,出口静压24.5 MPa,转速16 000 rpm,假定启动、关机阶段进出口参数及转速线性变化。通过建立表面效应单元,将流场仿真得到的叶片对流换热系数和主流温度插值到有限元模型上。

表2 载荷加载时间
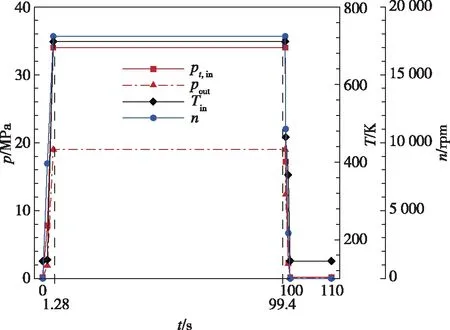
图2 涡轮进出口参数及转速变化Fig.2 Parameters at the inlet and outlet of turbine and speed
2 计算结果及分析
2.1 带冠涡轮叶片结果分析
图3给出了不同工作阶段结束时刻叶片上的温度分布,由于叶片较厚,而启动时间较短,启动阶段结束时叶片中心温度仍无变化,叶片上最大温差达到510 K;稳定工作阶段结束时,叶片温度分布稳定,基本上反映了流场温度,最高温度655 K,整个叶片上的最大温差不超过50 K,压力面侧温度高于吸力面侧,靠近叶顶和前缘的温度较高而根部靠近前缘位置温度较低;关机阶段结束时,叶片中心仍保持较高温度,而尾缘温度基本降至主流温度,叶片上最大温差480 K;经过冷却后,受叶冠对流换热的影响,叶顶中心温度接近叶片表面温度,而因轮毂的影响,叶根中心温度仍较高,最高温度307 K,叶片上温差有190 K。可以看出,叶片不同位置对叶片热载的响应速度差别大,在载荷变化过程中引起较大的温度梯度,加上结构约束使叶片变形受限,会导致叶片内产生大的应力。
各工作阶段结束时刻叶片上的等效应力分布如图4所示。启动阶段由于瞬时热冲击,导致整个工作过程最大应力的出现,最大应力为1 214 MPa。可以看出,大应力出现在叶片根部和顶部,特别是尾缘和前缘附近,以及吸力面侧叶根中部。分别取尾缘根部、尾缘顶部、叶根中部吸力面侧、前缘根部及前缘顶部区域最大应变幅点进行分析,分别记为A,B,C,D,E,如图4所示。
图5,6分别给出了叶片尾缘根部A点和顶部B点的径向应力-塑性应变滞回曲线。可以看出,根部节点A在第一次启动过程中产生最大塑性压应变,并在随后的循环中逐渐恢复;而顶部节点B在第一次启动过程中产生最大塑性拉应变,在之后的循环中,滞回环左移,残余塑性应变逐渐减小。对比两图可以看出,根部节点塑性应变远小于顶部节点,并且根部最大应力及应力幅值均低于顶部,说明该涡轮叶片中,低循环载荷对叶片顶部作用更大。
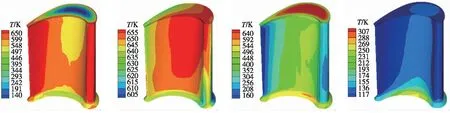
(a)压力面
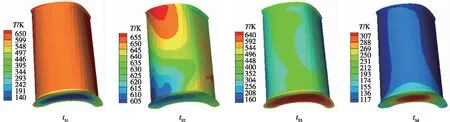
(b)吸力面图3 各阶段末叶片温度分布Fig.3 Temperature distribution at the end of each stage

(a)压力面
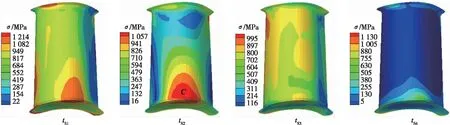
(b)吸力面图4 各阶段末叶片Von Mises等效应力分布Fig.4 Von Mises stress distribution at the end of each stage

图5 A点径向应力-塑性应变滞回曲线Fig.5 Radial stress-plastic strain hysteresis loops at node A
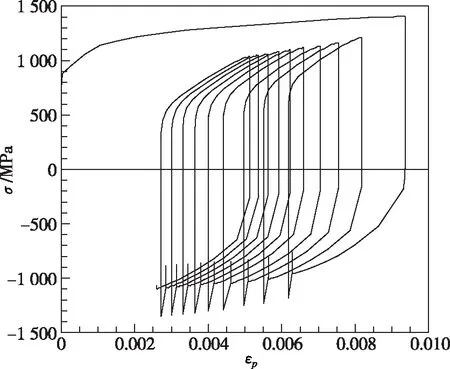
图6 B点径向应力-塑性应变滞回曲线Fig.6 Radial stress-plastic strain hysteresis loops at node B
表3给出了前10次工作循环中各个节点的应变幅值和低周疲劳损伤。可以看出,叶顶尾缘B点应变幅值最大,其次是顶部前缘E点,而根部各点应变幅值相对较小。

表3 不同位置节点应变幅值和低周疲劳损伤
2.2 不带冠涡轮叶片结果分析
各工作阶段结束时刻叶片上的等效应力分布如图7所示。可以看出,没有叶冠约束,叶片上整体的应力水平明显降低;叶片顶部成为自由端,应力很小,特别是尾缘,由于叶片尾缘薄,可以快速跟随环境温度变化,除了根部受约束以外可以自由膨胀,因此在开关机温度瞬态变化时,尾缘附近应力最小。另外,由于叶顶侧减少了约束可以自由膨胀,叶片尾缘根部的应力也得到释放,等效应力低于带冠涡轮相应位置的应力。取叶片根部尾缘、叶背和前缘区域的关键点A,C,D(见图4)进行分析。
图8给出了不带冠叶片和带冠涡轮叶片在一个工作循环中,根部不同位置节点的径向总应变和应力随时间的变化曲线。对于尾缘A点,由于不带冠叶片降低了对根部的约束,应变范围和最大应力略有降低。对于叶背C点,带冠叶片叶背根部产生塑性拉应变,因此总应变值高于不带冠叶片;而不带冠叶片中,尾部相对较大的变形导致叶背径向应力水平提高,因而径向应力最大值高于带冠涡轮,会对疲劳寿命产生不利影响。前缘D点的应变范围和最大应力增大。

(a)压力面
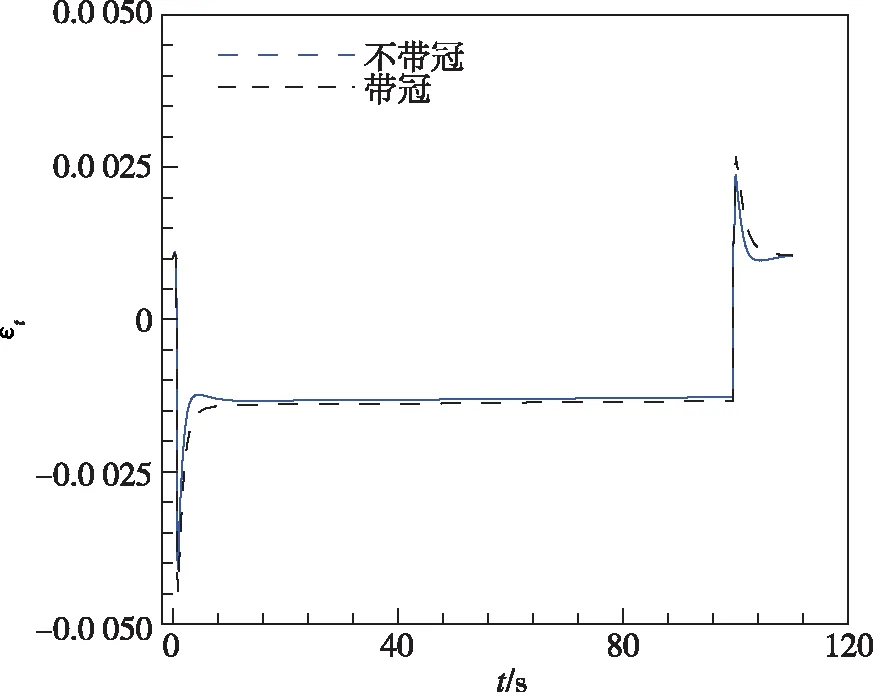
(a)尾缘A点应变
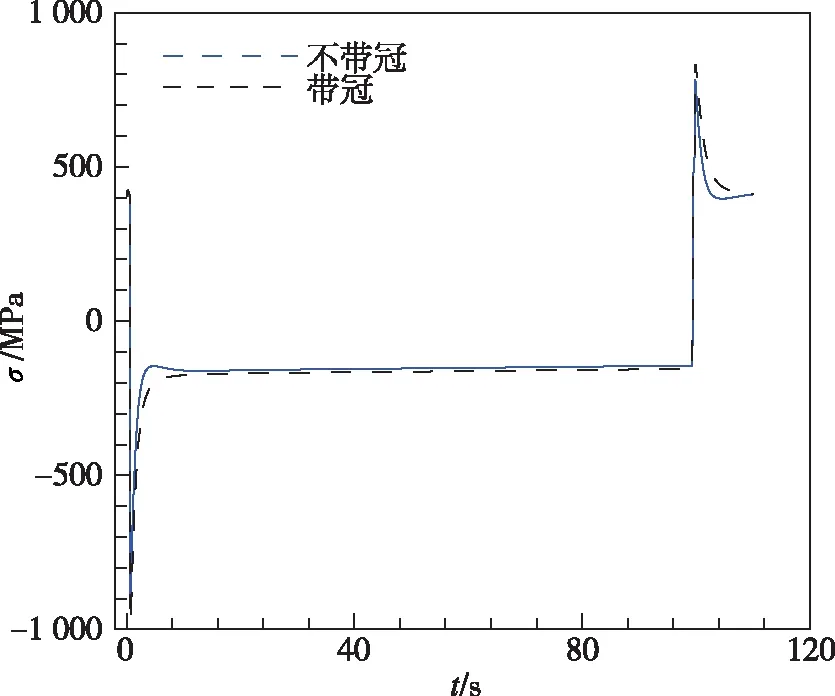
(b)尾缘A点应力

(c)叶背C点应变
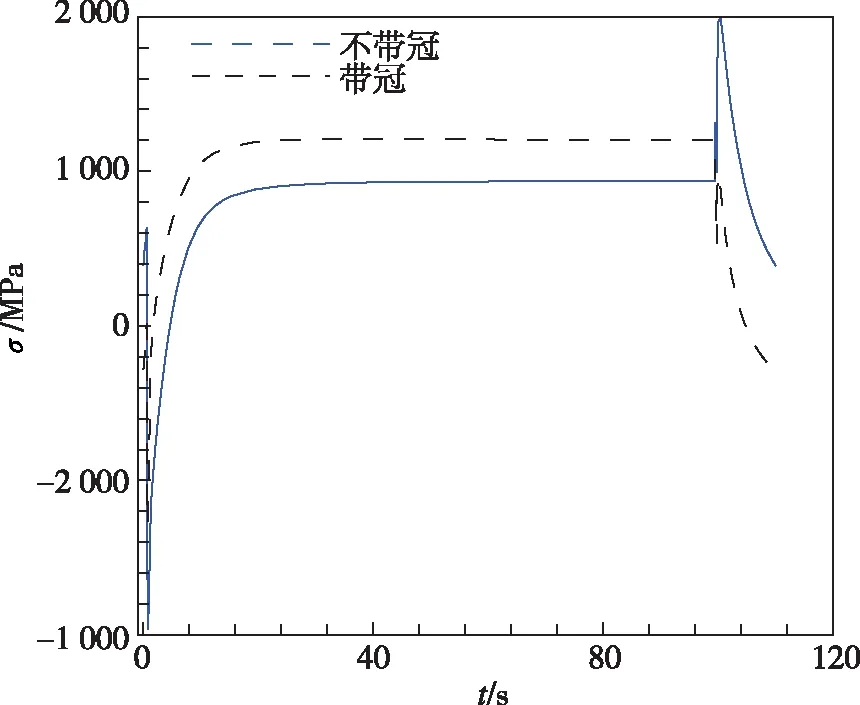
(d)叶背C点应力
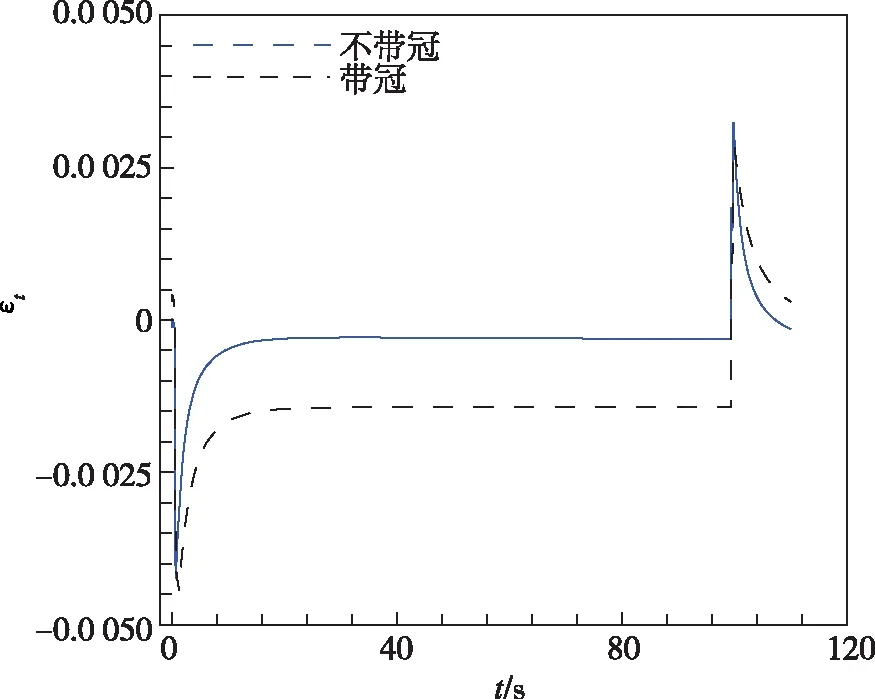
(e)前缘D点应变
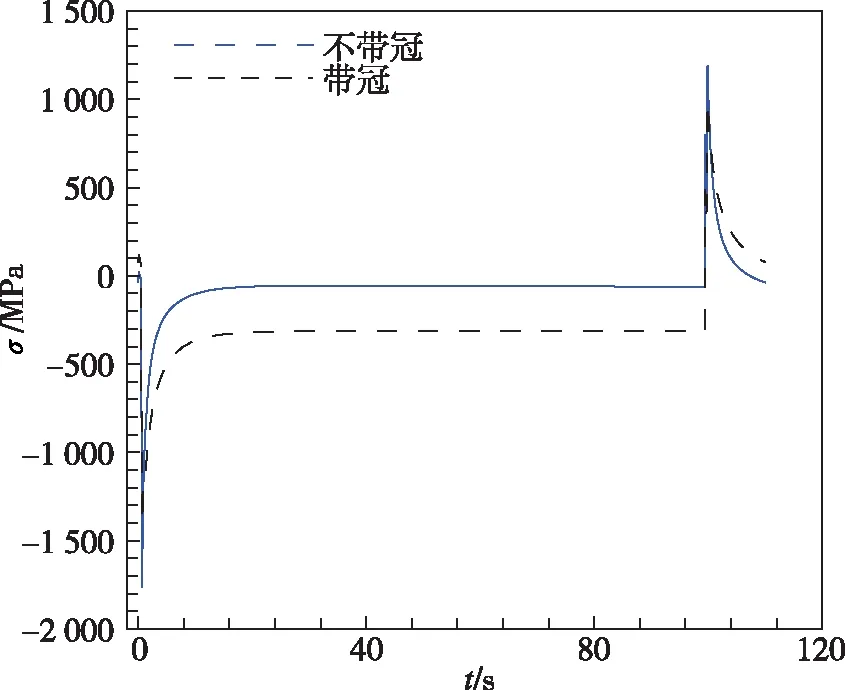
(f)前缘D点应力
表4中列出了前10次工作循环中,叶根不同位置节点的应变范围和低周疲劳损伤,叶背根部C点疲劳损伤最大,虽然其应变范围小,但是最大应力值高,导致疲劳损伤大;尾缘A点应力低,因此疲劳损伤较小。

表4 不同位置节点应变幅值和低周疲劳损伤
2.3 带部分冠涡轮叶片结果分析
各工作阶段结束时刻叶片上的等效应力分布如图9所示。可以看出,叶片根部尾缘、叶背和前缘区域依然是应力大的位置,因此仍然在这3个位置取关键点A,C,D进行分析。
图10给出了不带冠叶片和带部分冠涡轮叶片在一个工作循环中,叶背根部C点和前缘D点的径向总应变和应力随时间的变化曲线。对于叶背C点,带部分冠叶片的应变范围和最大应力均低于不带冠叶片,说明加上部分冠对叶背受力情况起到了改善作用。而对于前缘D点,带部分冠叶片的应变范围增大,应力也略有增加。
表5中列出了前5次工作循环中,叶根尾缘、叶背和前缘节点低周疲劳损伤,前缘D点损伤最大。
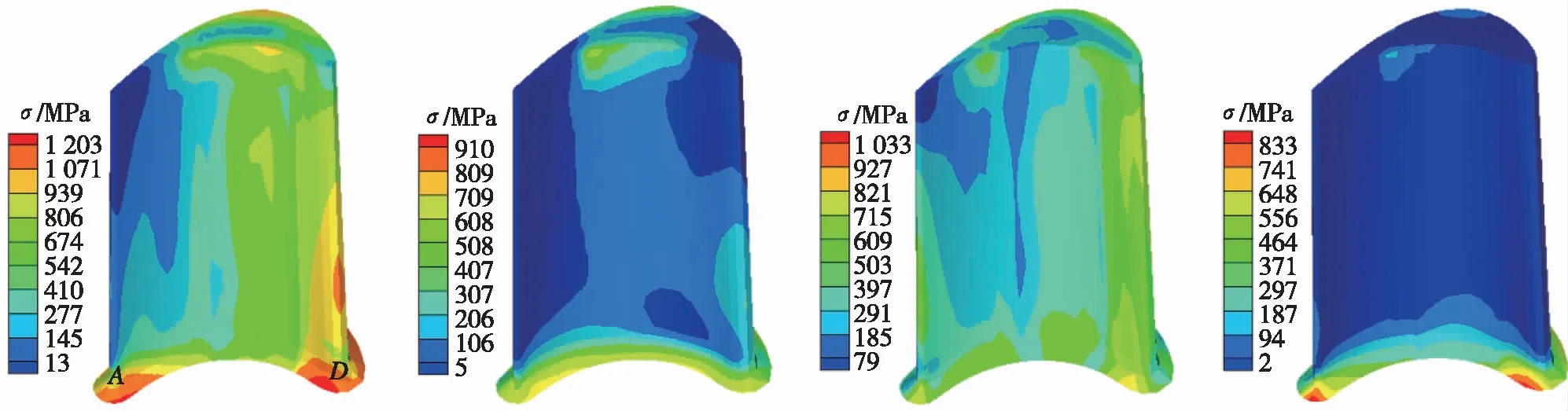
(a)压力面
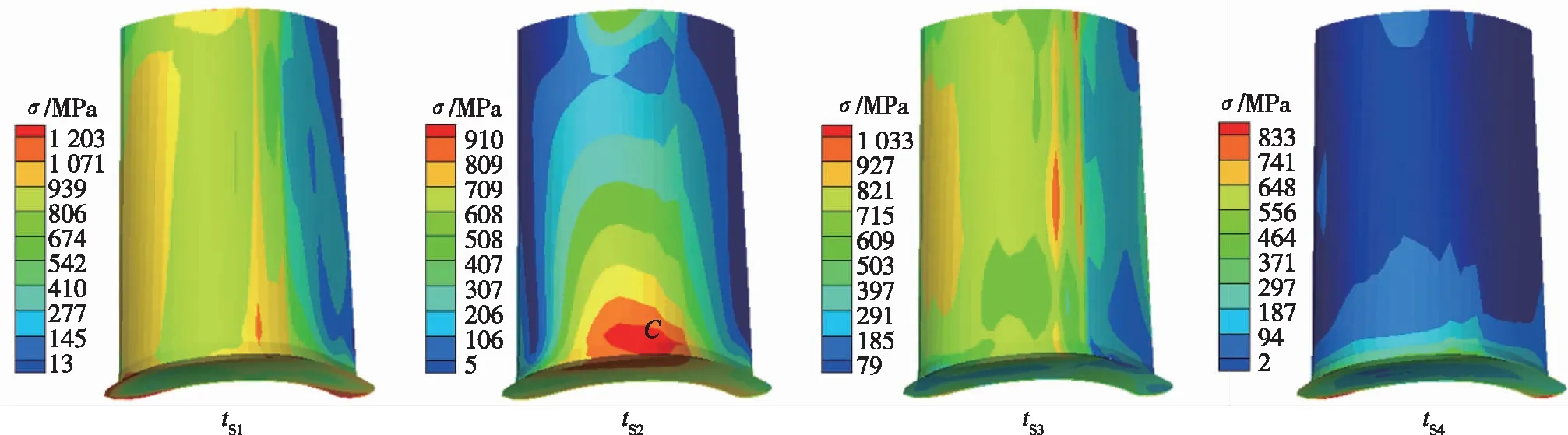
(b)吸力面图9 各阶段末叶片Von Mises等效应力分布Fig.9 Von Mises stress distribution at the end of each stage

(a) 叶背C点应变
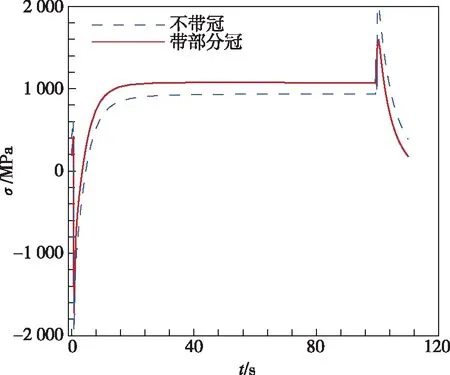
(b) 叶背C点应力

(c)前缘D点应变
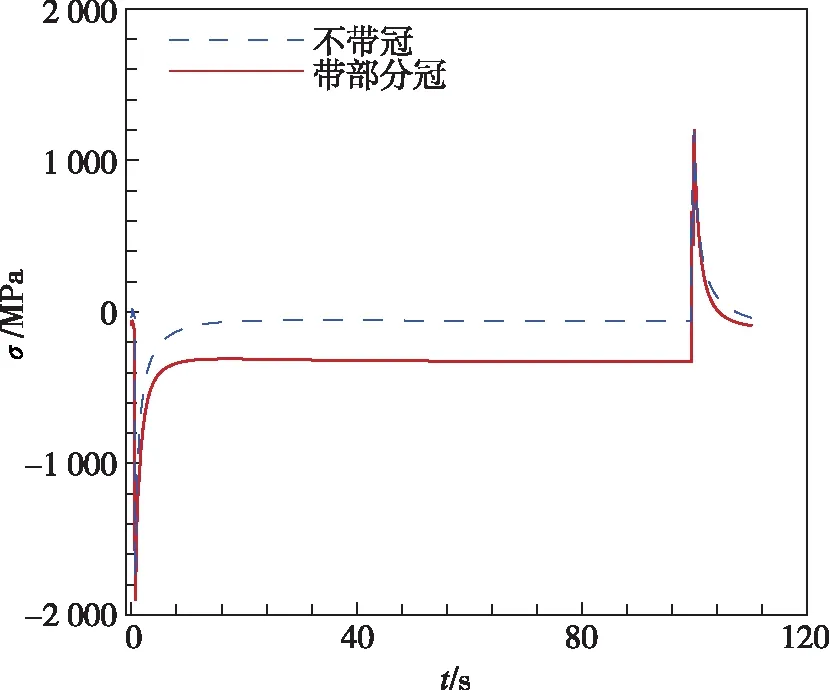
(d)前缘D点应力

表5 不同位置节点应变幅值和低周疲劳损伤
2.4 空心叶片结构结果分析
各工作阶段结束时刻叶片上的等效应力分布如图11所示。与图7不带冠叶片应力分布相比,除了后冷阶段最大应力略有增加,其他各阶段最大应力明显减小,且叶片上整体应力水平降低。取叶片根部尾缘、叶背和前缘区域的A,C,D点(见图11)进行分析。
图12给出了空心叶片和不带冠涡轮叶片在一个工作循环中,叶背根部C点和前缘D点的径向总应变和应力随时间的变化曲线。与不带冠叶片相比,空心叶片叶背根部的拉应变减小,压应变值增大,而应力明显减小;前缘应变范围减小,应力略有增大。
表6中列出了前10次工作循环中,叶根不同位置节点的应变范围和低周疲劳损伤。与表4不带冠叶片应变幅值相比,叶背应变幅变化不大,但最大应力明显减小;前缘应变幅降低,应力略有增大。
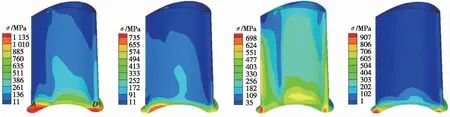
(a)压力面

(b)吸力面图11 各阶段末叶片Von Mises等效应力分布Fig.11 Von Mises stress distribution at the end of each stage

(a) 叶背C点应变
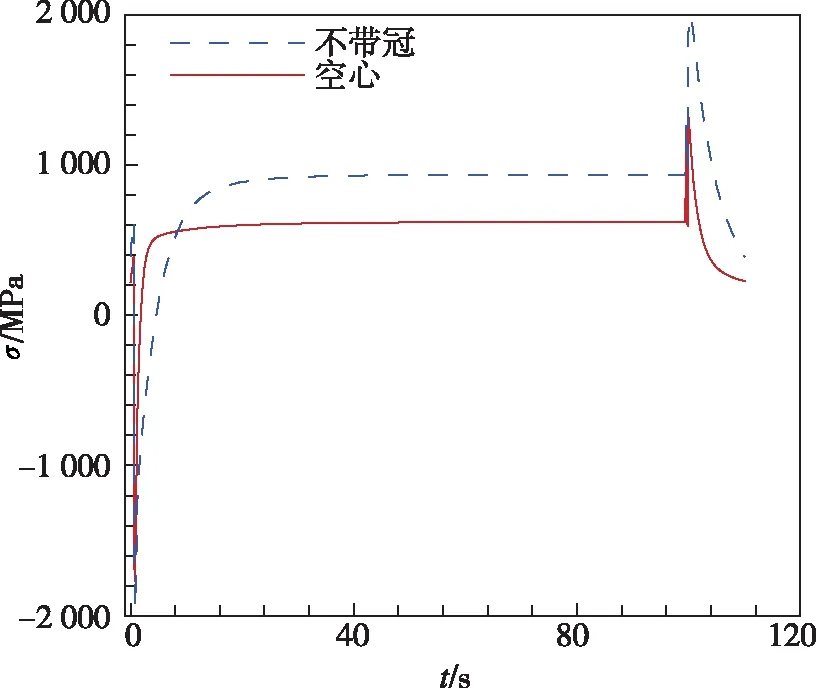
(b) 叶背C点应力

(c)前缘D点应变

(d)前缘D点应力
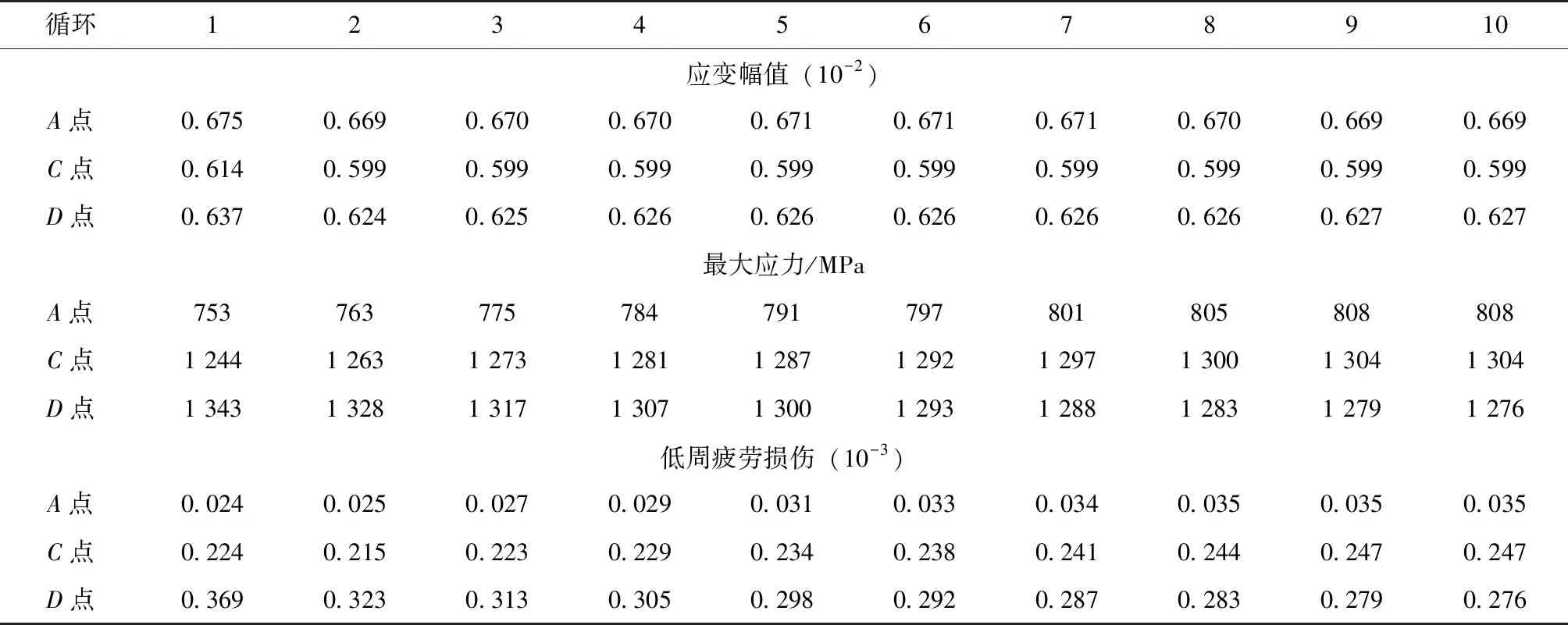
表6 不同位置节点应变幅值和最大应力
2.5 疲劳损伤及寿命对比分析
图13(a)给出了带冠涡轮叶片前10次工作循环中各个节点的损伤。可以看出,叶顶尾缘B点损伤最大,其次是顶部前缘E点,而根部各点损伤相对较小,根部尾缘A点低周疲劳损伤最小,每次循环损伤低于10-4。随着循环次数增加,损伤的变化量减小,10次循环后的损伤按照第10次循环的损伤值计算。
图13(b)给出了不带冠涡轮叶片前10次工作循环中,叶根不同位置节点的损伤,叶背根部C点疲劳损伤最大,虽然其应变范围小,但是最大应力值高,导致疲劳损伤大;尾缘A点应力低,因此疲劳损伤较小。与图13(a)带冠叶片损伤对比可以看出,尾缘根部A点损伤进一步减小,而叶背C点和前缘D点损伤比带冠涡轮相应位置的损伤都大,但低于带冠涡轮中顶部尾缘B点的损伤。总的来看,不带冠涡轮降低了损伤,但是由于热应力的存在,叶片厚度大的背部和前缘仍会产生较大的损伤。
图13(c)给出了前5次工作循环中,叶根尾缘、叶背和前缘节点的损伤,前缘D点损伤最大。与带冠叶片和不带冠叶片损伤对比可以看出,尾缘根部A点损伤进一步减小,叶背C点损伤低于不带冠和带冠叶片损伤,而前缘D点的损伤略有增加。
图13(d)给出了前10次工作循环中,叶根不同位置节点的损伤,与不带冠叶片的损伤相比,叶背和前缘的损伤均降低,说明叶片空心可以显著改善叶片疲劳情况。
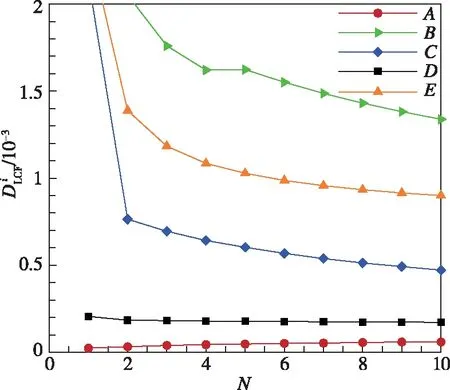
(a) 带冠叶片各点损伤
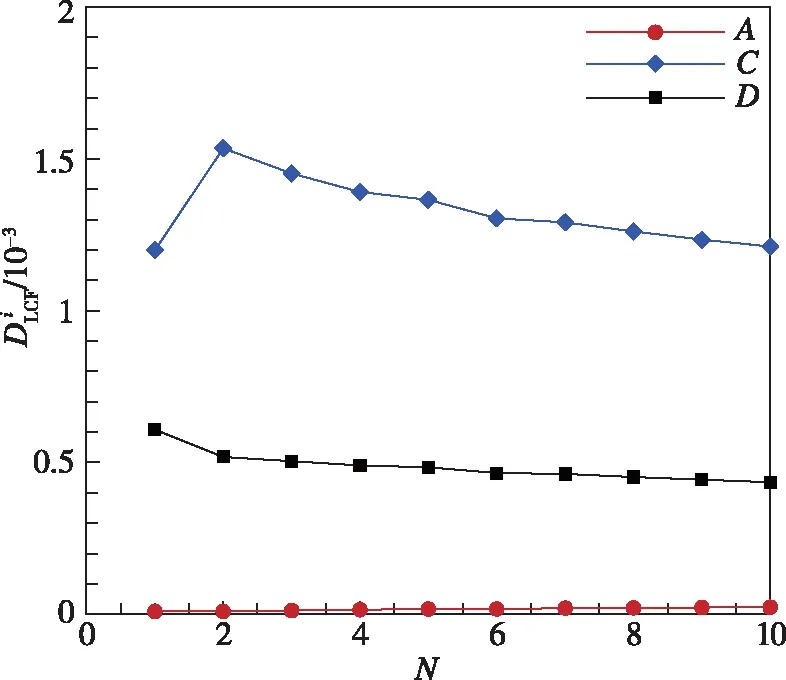
(b) 不带冠叶片各点损伤
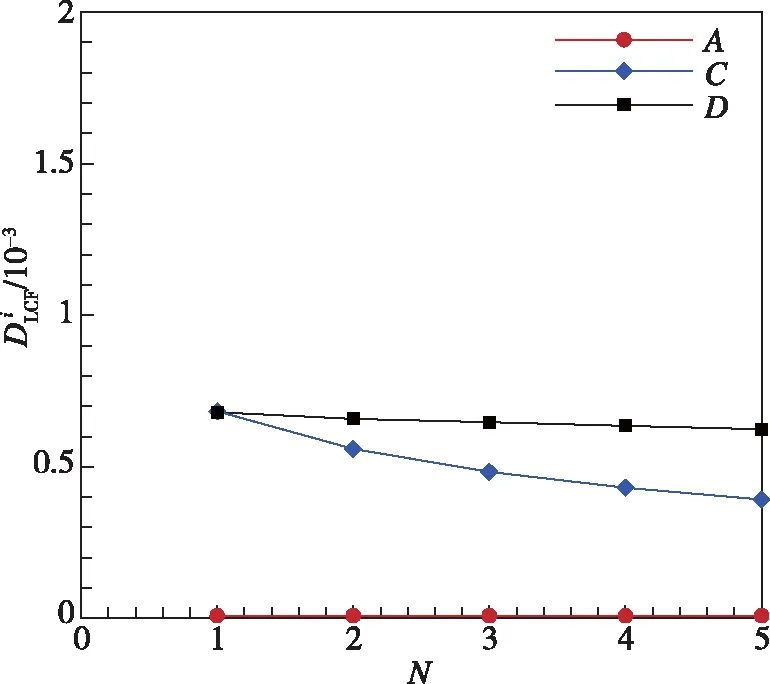
(c) 带部分冠叶片各点损伤
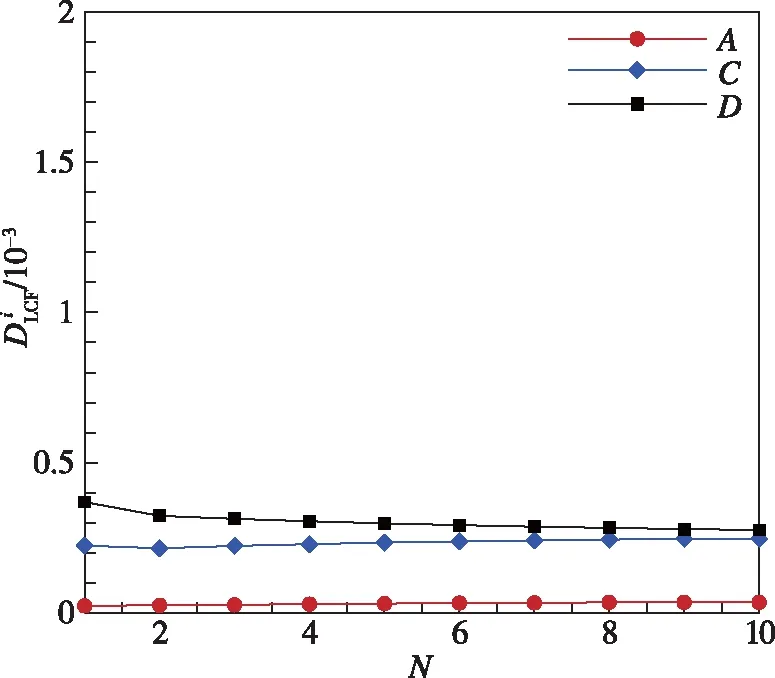
(d) 空心叶片各点损伤
表7列出了不同结构形式的叶片各关键节点及叶片疲劳寿命。与原带冠涡轮叶片相比,不带冠叶片危险点位于叶背根部,寿命提高11%;带部分冠叶片危险点位于前缘根部,寿命提高116%;空心叶片危险点位于前缘根部,寿命提高370%。显然,叶片空心结构减缓叶片疲劳的效果最好。

表7 不同结构形式涡轮叶片寿命
3 结论
以某火箭发动机涡轮为对象,研究了火箭发动机涡轮带冠、不带冠及带部分冠和空心叶片等典型结构形式对叶片疲劳寿命的影响,得到以下结论:
1)带冠叶片高应力出现在叶片根部和顶部,特别是尾缘和前缘附近,本文中,叶片危险点位于叶片尾缘顶部。
2)不带冠叶片可以消除叶片顶部的疲劳损伤,但使叶背根部损伤增大,本文中,叶片危险点位于叶背根部,比带冠叶片寿命高约11%。
3)带部分冠叶片在消除叶顶疲劳损伤的同时,还可以减缓叶背根部的疲劳,进一步提高疲劳寿命,本文中,叶片危险点位于前缘根部,比带冠叶片寿命高约116%。
4)叶片空心结构可以有效降低叶片根部的应力应变水平,减小疲劳损伤,提高叶片疲劳寿命,本文中,叶片危险点位于前缘根部,寿命比带冠叶片寿命高约370%。
