水下航行体齐射出筒“水锤”特性分析
2020-10-29魏英杰武雨嫣宋武超卢佳兴
魏英杰,武雨嫣,王 聪,宋武超,卢佳兴
(1. 哈尔滨工业大学航天学院,哈尔滨 150001;2. 湖北航天技术研究院总体设计所,武汉 430040)
0 引言
水下航行体是基于水下发射平台,采用高压气体弹射出筒,用以精确打击目标的航行器;齐射技术作为饱和攻击方式,是指多发航行体以一定发射空间间距在极短时间间隔内连续发射。水下航行体以齐射方式出筒可大幅提高攻击力,已作为现代水下发射常见的一种发射方式。
水下航行体齐射出筒后,筒内高压气体迅速溢出,排开筒口流体并导致筒内压力降低。当筒内压力降低至当地平衡状态时,外部流体便会在压力差的作用下大量涌入发射筒,对发射筒底部产生冲击,此现象称为“水锤”现象。据已有研究表明,“水锤”现象会对发射平台的发射筒强度产生重要的影响,同时引起发射筒的振动,甚至影响发射平台的升沉。因此,深入开展水下航行体出筒过程“水锤”特性分析,具有重要意义。
目前已有的对于航行体水下发射过程的研究,多针对于航行体受力及弹道特性。Dyment等[1]采用实验手段研究了航行体冷弹射出筒过程,并利用VOF多相流模型对该过程中尾空泡的形成与发展进行了数值模拟。Li等[2]采用Mixture多相流模型对水下航行体发射进行了数值模拟。Weiland等[3-4]研究得出发射深度、来流速度等发射参数对水下航行体出筒过程中受到的载荷影响规律。张红军等[5]采取Mixture多相流理论和动网格方法,对水平方向的来流影响下的航行体出筒运动过程进行了三维仿真计算。卢佳兴等[6]基于高速摄像技术对小型回转体齐射出水过程开展实验研究,通过对比单发、双发回转体的弹道特性,分析齐射出水过程中回转体间的相互干扰。
国内对于水下航行体出筒后海水倒灌入筒产生的“水锤”效应分析较少。2000年,倪火才[7]率先对水下航行体水下垂直发射时的“水锤”压力进行了试验研究,得到了发射筒底部“水锤”压力实验曲线。傅德彬等[8]对航行体发射的海水倒灌过程进行了数值模拟,并对影响涌入海水冲击压强的因素进行分析,发现发射筒底部附近的局部挡流板可有效降低涌入海水的冲击效应。周笑飞等[9]采用Fluent软件对筒内注水过程进行了三维仿真,得到了“水锤”周期内筒底压力与注水量的变化情况,并通过分析得到发射筒注水的规律,探究了“水锤”产生的机理。李强[10]基于单发航行体的发射实验,分析了发射平台表面和速度对筒口气团发展形态以及“水锤”效应的影响。李智生等[11]采用 CFD 方法对海水涌入发射筒后的流场特性和载荷特性进行了数值模拟计算,建立了“水锤”压力峰值估算模型,得到了不同工况下“水锤”效应的变化规律。
综上所述,现有的研究多集中于航行体出筒后的筒口流场特性分析,对于“水锤”现象的研究较少。且已有的研究均基于单发航行体出筒过程,对于齐射出筒过程的“水锤”特性研究尚无人开展。而实际水下发射过程中,为提高打击精度,往往采用多发航行体齐射技术,此时受航行体之间耦合运动的影响,流动特性变得更为复杂。本文基于SST湍流模型和VOF多相流模型,引入重叠网格技术,建立适用于水下航行体齐射出筒的数值计算方法。在此基础上分析齐射状态下“水锤”效应对首、次发射筒的影响机理,研究不同发射顺序下水锤效应的变化情况。
1 数学模型
1.1 控制方程
数值计算以Navier-Stokes方程为基础,通过求解质量守恒方程和动量方程,获得多相流场结构与流体动力。
混合介质质量守恒方程如下
(1)
式中,t代表时间,xi代表笛卡尔坐标分量,ui为笛卡尔坐标系下的速度分量,其中i= 1,2,3,分别对应了笛卡尔坐标系的3个坐标分量,ρm为混合介质密度。
动量守恒方程如下
(2)
式中,黏性剪切应力τij表达式为
(3)
式中,μm为混合物动力黏度,p为压强,S为源项,δij为Kronecker符号(当i=j时,δij=1;当i≠j时,δij=0)。
1.2 湍流模型
采用雷诺时均法(RANS)对于湍流流场进行求解,其表达式如下
(4)
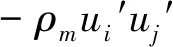
(5)
式中,k代表湍动能,μt代表湍动黏度。
本文采用SSTk-ω模型是一个与壁面函数相结合使用的低雷诺数湍流模型,其湍动黏度由湍动能k和比耗散率ω表示如下
(6)
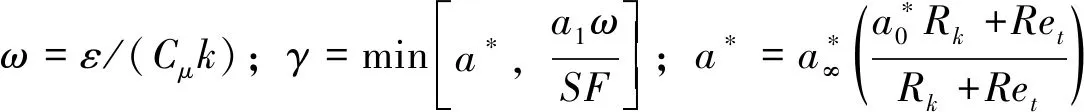
湍动能输运方程和比耗散率输运方程
(7)
(8)
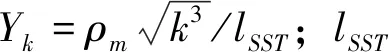
1.3 VOF多相流模型
VOF模型是一种在固定Euler网格下的表面跟踪方法,适用于需要得到一种或多种互不相融的流体介质间交界面的情况。在VOF模型中,不同的流体组分共用一套动量方程,计算时在全流场的每一个计算单元内,均记录下各流体组分所占有的体积率。
在本文所求解的气液两相流动问题中,液相为主相,其体积分数为αl,气相的体积分数为1-αl。
如图1所示,当αl=0时,该网格单元被气相充满,没有水相;当0<αl<1时,该单元格同时包含气相和水相,此时该单元格为两相交界面所在单元格;当αl=1时,该单元格被液相充满,没有气相。
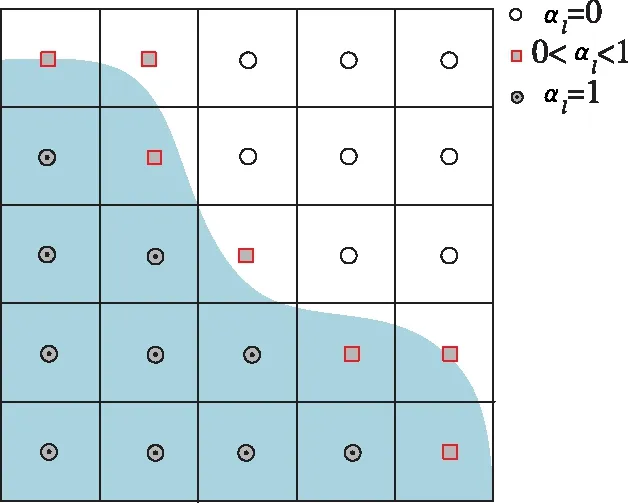
图1 VOF模型原理示意图Fig.1 Schematic diagram of VOF model
1.4 重叠网格技术
重叠网格又称为嵌套网格,它将流域分解为若干个子计算域,各子计算域计算网格在计算中相互独立,但网格之间又存在重叠、嵌套和覆盖关系。在重叠区域中,各子计算域网格通过流场信息的插值与映射进行数据交换,从而建立起各子计算域网格之间的耦合关系,为子计算域流场计算提供边界条件。
为确保背景区域和重叠区域之间的连通性,需要进行如下网格装配过程:
1) 挖洞,即用于确定活动单元、非活动单元和受体单元;
2) 寻找供体单元,确保每一个受体单元均能找到供体单元。
供体单元与受体单元上变幅值的通量满足如下关系
Φacceptor=∑αiΦi
(9)
式中,Φacceptor为受体单元通量,Φi为供体单元通量,α为插值加权因子。
2 计算模型及边界条件
水下航行体计算模型的直径为D(D=1 m),
长细比L/D=7,其中L为航行体的长度,采用抗空化椭球头型,航行体模型示意图如图2所示。
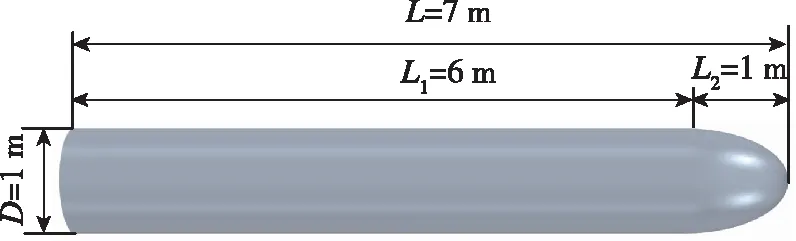
图2 航行体模型示意图Fig.2 Schematic diagram of sailing body model
为节省计算资源,采用1/2计算域模型。计算域划分示意图如图3和图4所示,其中背景流体计算域整体尺度为14D×11D×4D,发射筒长度为10D,发射筒直径为1D,即发射筒与航行体表面紧密接触;重叠计算域长度为8.8D,直径为1.4D。为模拟有发射平台速度工况下的水下齐射,赋予背景域速度入口和压力出口边界条件,发射筒底部赋予质量流量入口边界条件,通过用户自定义场函数指定入口处压力随时间变化关系。
为捕捉发射筒内以及筒口处附近的复杂的流场变化情况,对发射筒内以及筒口上方部分流域的网格进行了局部加密处理,加密区网格尺寸为50 mm。为减少网格数量,节省计算资源,在远场边界设置较大的网格尺度。
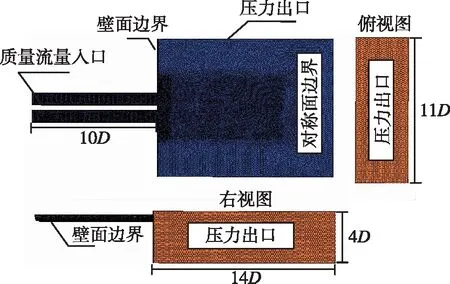
图3 背景域边界条件及网格划分Fig.3 Boundary conditions and mesh generation in background domain
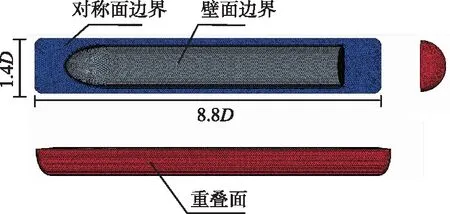
图4 重叠域边界条件及网格划分Fig.4 Boundary conditions and mesh generation in overlapping domain
3 数值计算方法验证
为验证数值计算方法的有效性,给出了筒底发射压力为0.2 MPa时,单发航行体无发射平台速度出筒工况下数值计算结果与试验结果的对比。
图5给出了筒口气团形态的数值计算与试验结果对比,其中以航行体尾部完全出筒时刻作为初始时刻,选取4个典型时刻的流场图。从图5中可以看出,数值计算与试验得到的筒口气团形态相似。航行体尾部完全出筒后,筒内气团溢出并近似成为一个闭合于航行体尾部的圆柱形空泡,如图6给出了筒底压力的数值计算与试验结果对比。从图6中可以看出,数值计算结果与试验结果具有相似的变化趋势。航行体尾部出筒后,筒内压力持续性振荡,振荡幅度逐渐减小,周期近似为常数。t=50 ms时,筒内达到第一个压力峰值,即对应图5(c)中气团拉断瞬间。在整个过程中,数值计算结果振荡幅度高于试验结果,这是由试验过程无法及时关闭通气阀造成的。

(a) t=5 ms

(b) t=35 ms

(c) t=50 ms

(d) t=55 ms图5 筒口气团形态对比Fig.5 Comparison of the shape of the air mass at the mouth of the cylinder
t=35 ms所示。当筒内气体压力低于环境压力时,在外界水压的影响下,发射平台壁面附近气团膨胀速度逐渐减小直至反向收缩,直至发生截断,随后形成了回射流,如t=50 ms,t=55 ms时所示。
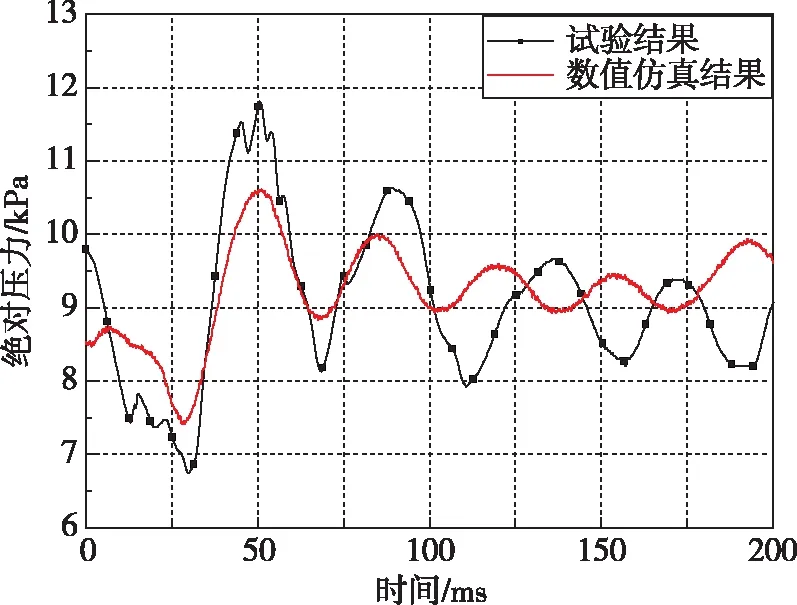
图6 筒底压力曲线对比Fig.6 Pressure comparison of cylinder bottom
综合来说,数值计算结果与试验结果均符合良好,验证了该数值计算方法对计算航行体出筒过程流场以及筒内压力特性的有效性。
4 典型工况计算结果及分析
本文选取顺序发射为典型工况,顺序发射是指沿水平来流的方向,位于上游的航行体率先发射出筒,下游航行体以固定时间间隔依次发射,示意图如图7所示。发射平台速度为2.0 m/s,横流方向为x轴正方向,最大筒底压力为0.7 MPa,发射时间间隔为0.85 s。
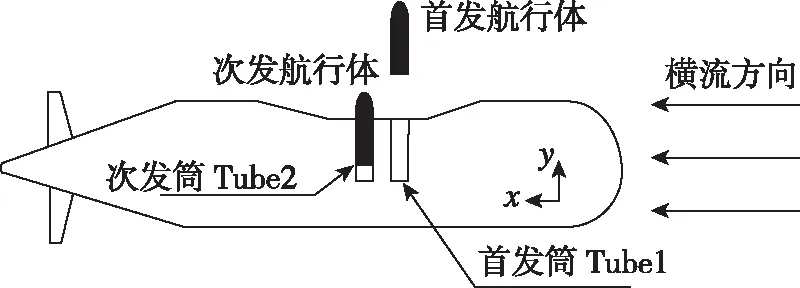
图7 顺序发射示意图Fig.7 Schematic diagram of sequential launch
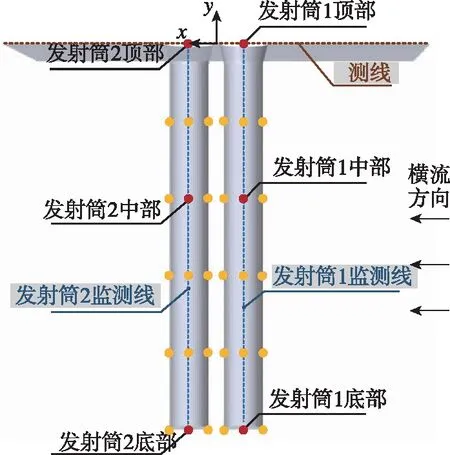
图8 压力监测点(线)分布示意图Fig.8 Distribution diagram of pressure monitoring points (lines)
发射筒内压力监测点及压力监测线分布情况如图8所示。在每个发射筒筒内设置16个压力监测点记录筒内压力变化规律,在发射平台表面以及首、次发射筒中心线设置压力监测线。其中标记点为压力的数据提取点,分别位于首、次发射筒口、筒中和筒底3个典型横截面中心线上。图8中对坐标系进行了定义,坐标原点位于两发射筒筒口连线的中点,典型工况下首发筒口中心点位于x负半轴,次发筒口中心点位于x正半轴。
4.1 流场特性分析
图9给出了典型工况下首、次发航行体尾部完全出筒后的压力云图与空泡形态图。时间零点分别为首、次发航行体尾部完全出筒时刻。从图9中可以看出,航行体发射出筒后,两发射筒内均出现明显的压力振荡。首发航行体尾部完全出筒后,筒内高压气体向筒外作轴向扩张,形成筒口气团,筒内压力降低(图9(a) Ⅱ)。当气团压力小于当地的环境压力时,在周围流体的作用下转为径向收缩,导致气团内部及筒内压力增高(图9(a) Ⅲ)。随着外部流体不断侵入,气团被截断为两个主空泡,一部分附着于航行体尾部形成尾空泡,另一部分位于发射筒口。气团拉断处形成两个高压区,分别沿轴向上下两个方向推移,产生回射流,外部流体向下涌入发射筒,与筒内气体发生强烈的相互作用,压缩筒内气体导致压力持续升高(图9(a) Ⅳ),即为第一个振荡周期。
次发航行体完全出筒后,受首发航行体筒口流场的影响,产生了更大的筒口气团,筒口气团在膨胀过程中不断挤压筒口附近流体,使首发筒内压力升高(图9(b) Ⅰ)。由图9(b) Ⅲ可知,次发航行体出筒后0.30 s,筒口气团被截断形成附体尾空泡,由于横向来流作用,下方气团冲击至发射平台表面导致局部压力升高,与此同时少部分流体涌入发射筒,压缩筒内气体,在发射筒内产生相比于首发筒较小的压力幅值。
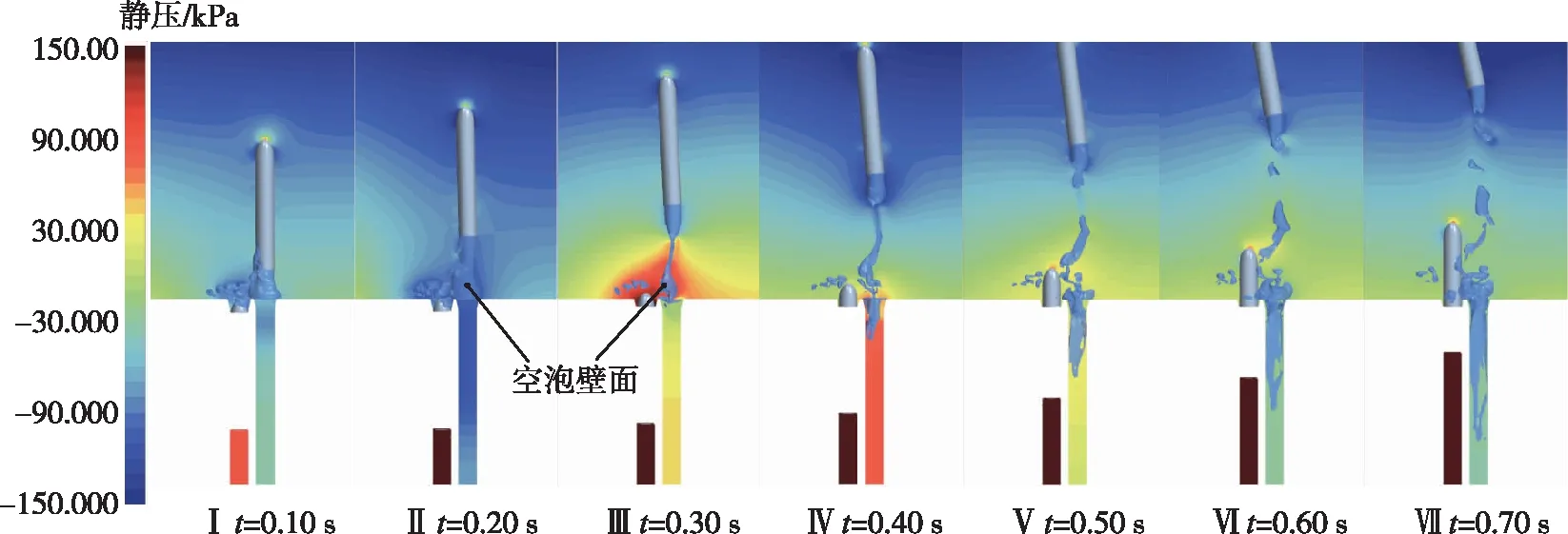
(a)首发航行体出筒
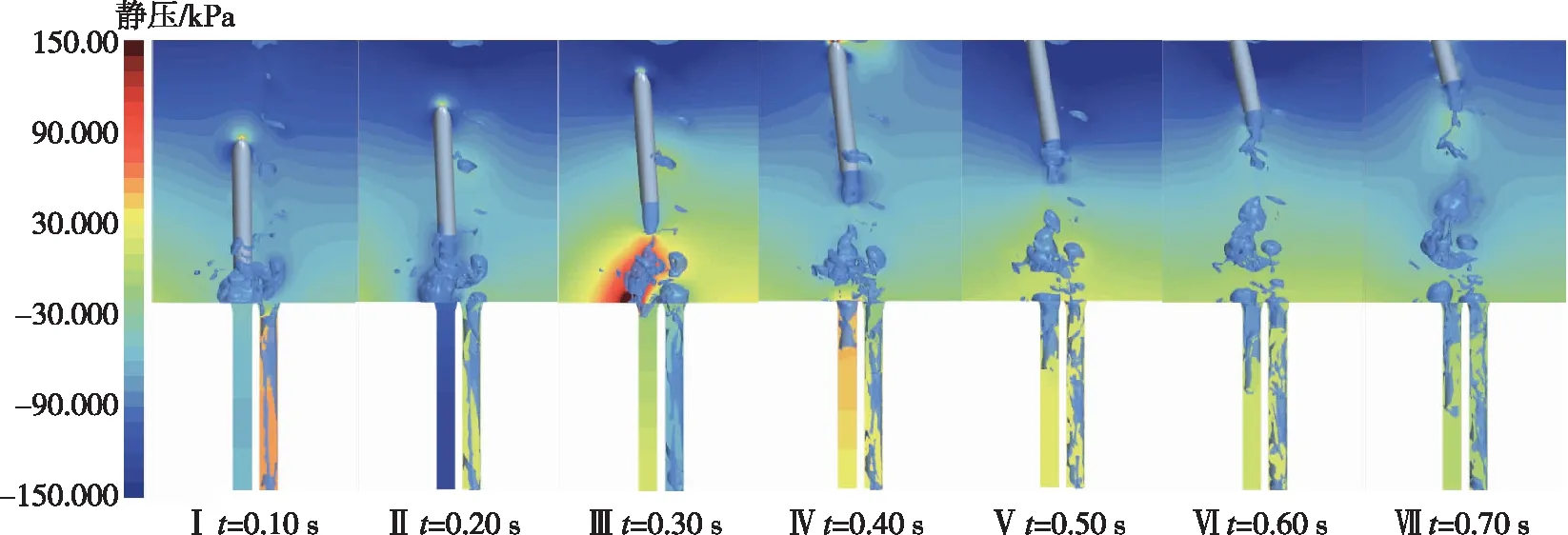
(b)次发航行体出筒图9 顺序发射过程流场压力云图与空泡形态图Fig.9 Pressure contour and cavity morphology of flow field in sequential launching process
4.2 发射筒内压力波动分析
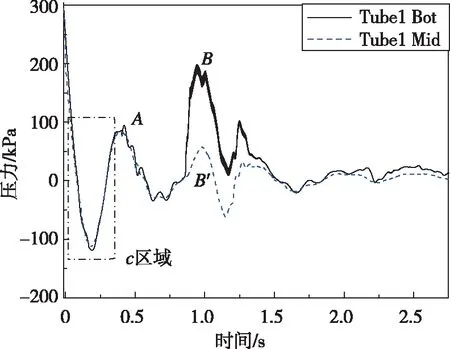
为分析“水锤”现象对发射筒不同位置高度处压力变化的影响规律,图10给出了首、次发射筒筒中和筒底的压力曲线对比,其中首、次发航行体尾部完全出筒时刻为时间零点。
由图10(a)可以看出,首发航行体尾部出筒瞬间,筒内高压气体迅速向外溢出,气体的内能转化为航行体和水的动能,高压气体的瞬间释放具有较大的能量,使得发射筒内的压力产生剧烈衰减。此后伴随筒口气团受压收缩直至截断,筒口的水开始涌入发射筒,压缩筒内气体,使得筒内压力升高到静压值。由于流体惯性作用,进一步压缩筒内气体,发射筒内压力持续上升,进而产生下一周期的压缩波。第一个振荡周期内,筒底与筒中压力大小基本一致。
不同于第一个压力峰值A,在峰值B处筒底与筒中压力值出现较大差异,位于发射筒底部的Tube1 Bot监测点出现最大的压力值。结合图9(b)Ⅰ,发现此时次发航行体出筒,次发筒口气团膨胀挤压首发筒口附近流体,导致首发筒内压力整体升高,筒中压力监测点Tube1 Mid出现第2个较小压力峰值B′;并且此时流体倒灌入筒,在惯性力作用下向下加速冲击至发射筒底部,由于次发航行体出筒影响与流体冲击的叠加作用,发射筒底产生较大的压力峰值B。对比两条曲线可以发现,流体冲击作用对压力影响更大。
由图10(b)可以看出,次发筒内第一个压力峰值相对首发筒较小,结合图9(b) Ⅲ,发现气团拉断产生的回射流在横向来流作用下冲击至发射平台表面,削弱了流体对发射筒的冲击作用。次发航行体出筒后约1.06 s,倒灌入筒的流体冲击筒底产生幅值较大、持续时间极短的压力峰值,峰值出现时间较首发筒有所推迟。
(a)首发筒
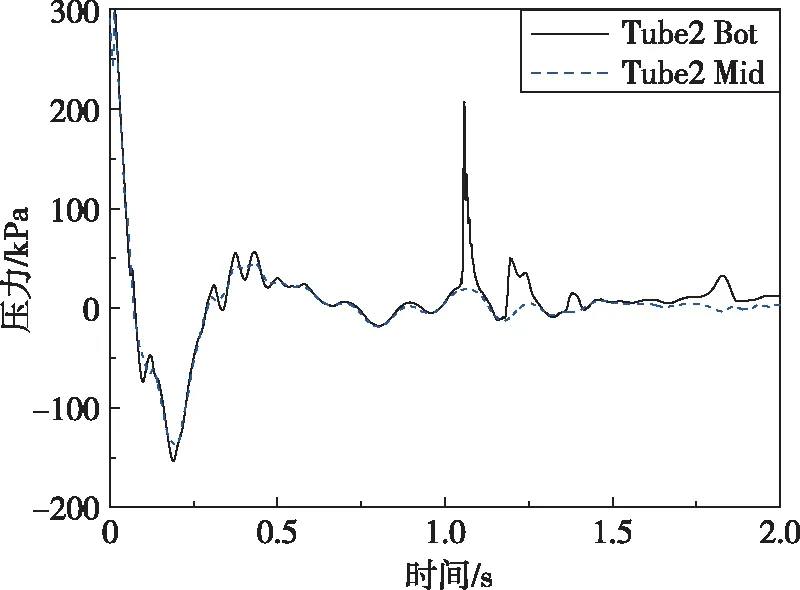
(b)次发筒图10 发射筒不同位置处压力曲线对比Fig.10 Comparison of pressure at different positions of launching cylinder
为分析首发航行体出筒后首发筒处流场对于次发筒口压力波动的影响,图11给出了首、次发筒口压力变化曲线对比,两条曲线均以首发航行体出筒时间为t=0时刻。分析曲线发现,首发航行体出筒后,筒内高压气体迅速向筒口溢出,筒口处形成较大的压力峰值(图11中C点)。同时在次发筒口形成幅值较小,时间略延后的压力峰值(图11中C′点),其数值约为首发筒口的1/2。随后由于流体灌入发射筒和航行体高速离开发射筒,两发射筒口压力迅速下降。在经历了一个波谷后,筒口压力在外部流体挤压作用下转而升高,达到第2个峰值(图11中D点)。之后压力小幅度波动,波动幅值逐渐减小。
当t=0.85 s时,次发航行体完全出筒,筒内高压气体溢出,于次发航行体筒口产生第2个幅值最大的压力峰值,约为300 kPa,同时在首发航行体筒口造成第3个压力峰值(图11中E点),随后其压力变化规律与之前类似,经历波谷后,筒口压力达到较小的峰值(图11中F点)。图11中t=0.1 s到t=0.85 s对应次发航行体出筒过程,航行体完全运动至筒口监测点处,此时不存在压力数据。
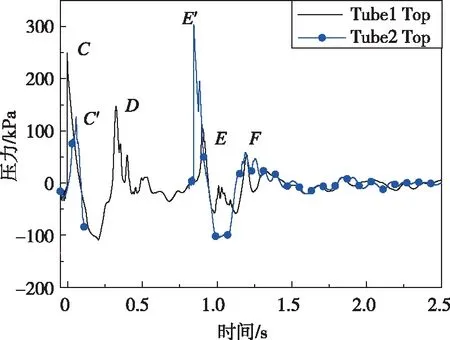
图11 首、次发筒口压力曲线Fig.11 Pressure curve of primary and secondary cylinder
对比发射筒不同位置高度处压力变化规律,发现筒口压力振荡峰值高于筒内,低于筒底,且振荡频率较高。这是由于发射筒口的压力振荡主要由筒口气团的压缩波振荡导致的高频振动,而筒内的压力振荡是压缩波的高频振动和水倒灌产生的低频振动叠加形成的。对比首、次发射筒压力变化规律,发现次发筒内压力振荡幅度小于首发筒,而筒口压力振荡情况较首发筒剧烈。
为分析一个振荡周期内发射筒内压力分布情况,图12给出了不同时刻首、次发射筒中心线上的压力分布曲线对比,其中y指发射筒中心线上纵坐标。分别取首、次发航行体完全出筒后第一个波动周期,如图10(a)中c区域所示,每隔0.05 s提取一组数据。

(a)首发筒

(b)次发筒图12 首、次发筒内压力分布曲线Fig.12 Pressure distribution curve of primary and secondary cylinder
观察曲线可以看出,首发航行体尾部完全出筒0.05 s时,此时发射筒底部边界由压力入口变为壁面边界条件,即发射筒底切断高压气体供应,原有筒内高压气体仍具有向上的动能导致发射筒底部压力被抽取而降低。出筒后0.1 s,筒内气体溢出,导致压力降低,此时最低压力出现在筒口下方1 m的位置。出筒后0.15 s时,对应压力云图9(a)Ⅱ,此时筒内压力进一步降低,最低压力出现在筒口下方6 m的位置,显示出筒内气体周期性振荡的过程。出筒后0.2~0.35 s,筒内压力逐渐上升,对应图10(a)c区域的后半段,此时流体开始倒灌入筒,并压缩筒内空气,使得压力升高。次发与首发筒内压力具有相似的规律。
首发航行体出筒后0.3 s时,筒口处压力出现较大范围的波动,其差值约为100 kPa,对应时刻的压力和速度如图13所示。由图13可以看出,此时外部流体开始灌入发射筒并与筒内气体发生剧烈的相互作用,于筒口处产生较大速度,进而引起压力的降低。
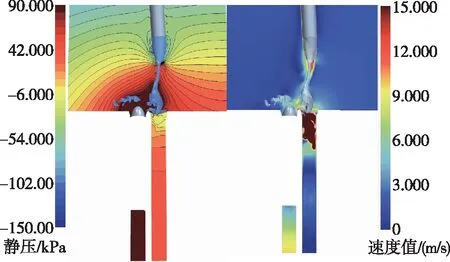
图13 首发航行体出筒0.3 s压力及速度云图Fig.13 Pressure and velocity contours of the primary sailing body after launching 0.3 s
4.3 发射平台表面压力波动分析
为分析筒口气团对平台表面的冲击作用,在发射平台表面设置压力监测线,监测线分布如图8所示。图14和图15给出了首发和次发航行体出筒后0.35 s时间内发射平台表面的压力分布情况。从图中可以看出,首发航行体出筒后在筒口形成高压区,随后压缩波振荡,引起筒口压力振荡。且由于顺序发射水平来流的作用,首发航行体出筒后,其筒口气团在次发筒口形成更加剧烈的振荡,而次发航行体出筒对首发筒口压力影响较小。次发航行体出筒0.30 s时,筒口下游出现较大的压力峰值,结合图9(b) Ⅲ可以发现,此时尾空泡被拉断形成附体尾空泡,产生的回射流在来流作用下撞击下游平台表面,产生压力峰值。
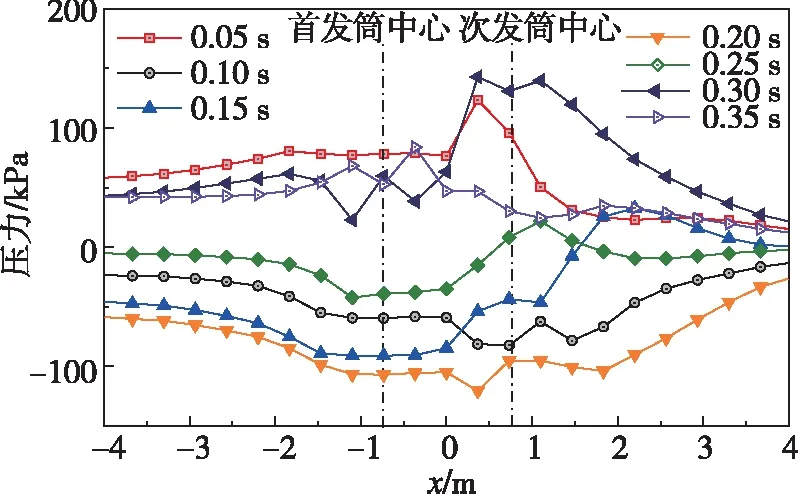
图14 首发航行体出筒0.35 s内发射平台表面压力分布曲线Fig.14 Pressure distribution curve of the launch platform surface within 0.35 s after the primary sailing body launching
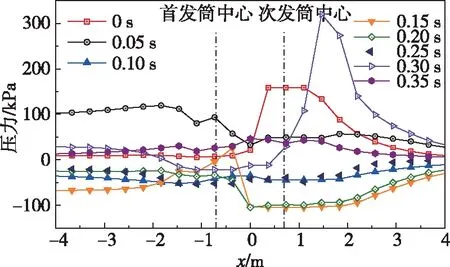
图15 次发航行体出筒0.35 s内发射平台表面压力分布曲线Fig.15 Pressure distribution curve of the launch platform surface within 0.35 s after the secondary sailing body launching
5 发射时序对“水锤”特性影响分析
水下航行体共架垂直并联发射过程中,发射顺序对于发射特性具有较大影响,主要表现在首发航行体发射出筒后,其尾空泡及筒口高压气体受相对发射平台的水平来流作用而发生运动,进而对次发筒口流场产生影响,同时次发航行体尾流场对首发筒的作用也会出现不同。本节研究了不同发射顺序时的“水锤”效应,主要分析顺序和逆序发射情况下首、次发筒的压力时间和空间分布情况。其中逆序发射是指沿水平来流的方向,位于下游的航行体率先发射出筒,其上游航行体以固定时间间隔依次发射。图16给出了逆序发射示意图。
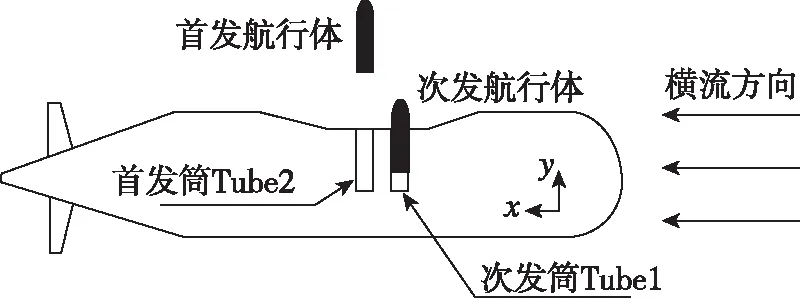
图16 逆序发射示意图Fig.16 Schematic diagram of reverse order launch
5.1 流场特性分析
图17给出了逆序发射工况下首、次发航行体尾部完全出筒后的压力云图与空泡形态图。时间零点分别为首、次发航行体尾部完全出筒时刻。由图17可以发现,与顺序发射时不同,逆序发射次发航行体出筒后,其尾部气团在水平来流的作用下向上卷起的同时朝首发筒口偏移。次发航行体出筒0.45 s时(图17(b)Ⅴ),外部流体开始涌入次发筒,并在筒口下游位置造成局部高压。相比于顺序发射,流体涌入次发筒的时间较为延后。次发航行体出筒0.65 s时(图17(b) Ⅶ),于首发筒产生第三个幅值较大的压力峰值。
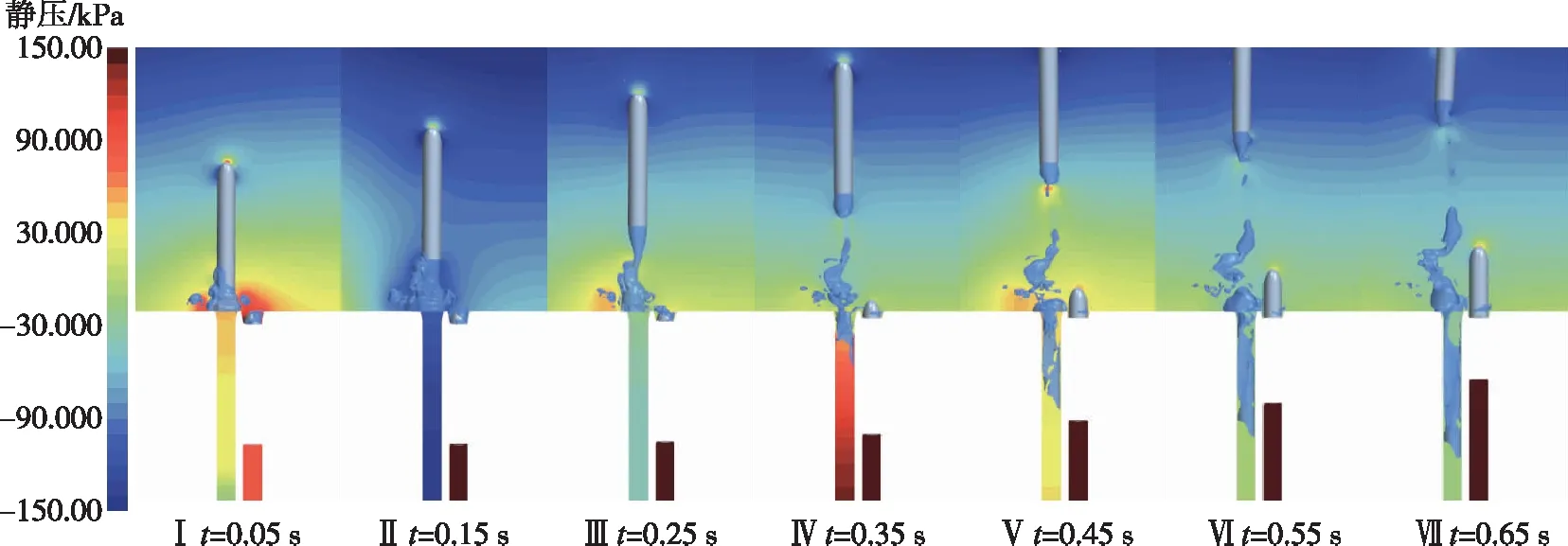
(a)首发航行体出筒

(b)次发航行体出筒图17 逆序发射过程流场压力云图与空泡形态图Fig.17 Pressure nephogram and cavity morphology of flow field in reverse order launching process
5.2 发射筒内压力波动分析
图18给出了逆序发射工况下首、次发筒内压力变化曲线,并与顺序发射工况对比。由图18(a)可以发现,在t=1.2 s内,不同发射顺序下首发筒内压力具有相似的变化趋势和振荡峰值。此后,顺序发射首发筒内压力振荡发生较大程度的衰减,而逆序发射筒内产生第3个周期的压力振荡。结合图19速度矢量图可以发现,由于横向来流的作用,次发筒口气团偏移至首发筒,造成第3个周期的压力振荡。
由图18(b)可以发现,两种发射顺序下次发筒内第一个压力峰值出现的时间相近、大小相似。随后逆序发射工况次发筒内压力逐渐降低,t=0.6 s时压力降低至谷值,而顺序发射次发筒内压力并未出现明显的谷值,这是由于次发筒口高压区的影响(图9(b) Ⅲ),导致次发筒内的压力振荡受到抑制。

(a)首发筒
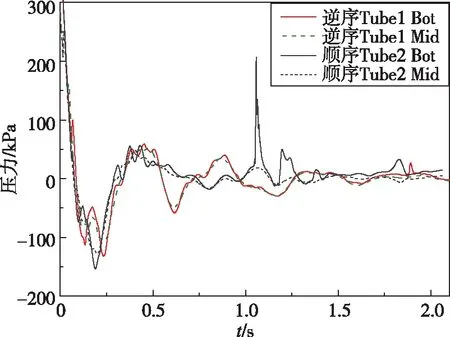
(b)次发筒图18 发射筒不同位置处压力曲线对比Fig.18 Comparison of pressure at different positions of launching cylinder
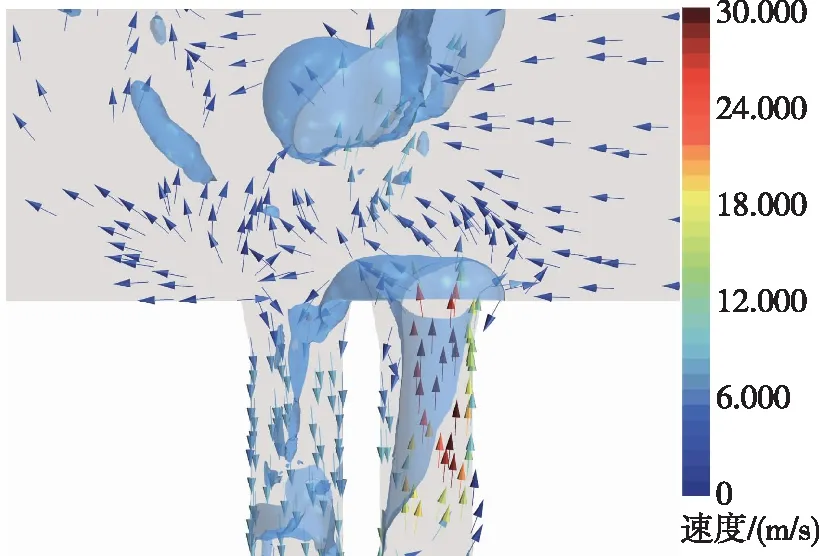
图19 次发航行体出筒0.55 s速度矢量图Fig.19 Velocity vector diagram of the secondary sailing body after launching 0.55 s
6 结论
本文基于重叠网格技术,针对水下航行体齐射出筒过程的“水锤”特性开展数值模拟研究,分析了齐射状态下“水锤”效应对首、次发射筒内压力振荡的影响规律,并研究不同发射顺序下水锤效应的变化情况,得到以下结论:
1)航行体尾部完全出筒后,筒内高压气体向筒外扩张,形成筒口气团,筒内压力降低。气团在外部流体挤压作用下体积收缩,压力增高。气团拉断瞬间产生回射流,导致外部流体开始涌入发射筒,与筒内气体发生强烈的相互作用,压缩筒内气体导致压力持续升高,即为首个振荡周期。此后在惯性作用下往复振荡。
2)次发航行体出筒对首发筒内压力的影响在于:次发航行体出筒后,其筒口气团膨胀挤压首发筒口附近流体,导致首发筒内压力升高产生第2个压力峰值;首发航行体对次发筒的影响主要集中于筒口,首发航行体出筒后,在次发筒口形成压力峰值,并引起次发筒口压力振荡。
3)发射顺序对“水锤”特性的影响在于,逆序发射工况下次发筒口气团由于水平来流作用偏移至首发筒,使首发筒内产生第3个周期的压力振荡。
