自动驾驶车辆循迹路径生成算法研究

李晋津 孙二鑫 陈宗娟

摘 要：在无人驾驶领域中 已经实现了车辆按照已有路径进行循迹无人驾驶 通常已有路径是由车辆实际采集获得。文章采用Matlab编写了循迹路径的生成算法 解决了循迹路线必须由车辆采集获取的问题 使车辆控制更加高效。再循迹路径生成算法中结合了车辆的左右转最小拐弯半径约束和允许倒车的情况 得到了无人驾驶车辆可行驶的路径。最后通过算法生成的路径进行了实车实验 车辆能够按照算法生成的路径进行自动驾驶 最后对算法生成的路径和车辆实际路径进行了对比 验证了算法的可行性。

关键词：路径生成;倒车;车辆转弯半径;实车实验

中图分类号：U495  文献标识码：A  文章编号：1671-7988（2020）18-16-06

Abstract： In the field of unmanned driving， it has been realized that vehicles follow existing paths to track unmanned driving， Usually the existing path is obtained by actual vehicle collection. this paper uses Matlab to write the algorithm of generating the tracing path， which solves the problem that the tracing route must be acquired by vehicle collection and makes the vehicle control more efficient. The re-tracking path generation algorithm combines the vehicle's left-right tur -ning minimum turning radius constraint and the allowable reversing situation to obtain a path that can be driven by an unmanned vehicle. Finally， a real-vehicle experiment was performed on the path generated by the algorithm. The vehicle can drive automatically according to the path generated by the algorithm. Finally， the path generated by the algorithm is compared with the actual path of the vehicle to verify the feasibility of the algorithm.

Keywords： Path generation; Reversing; Vehicle turning radius; Real car experiment

CLC NO.： U495  Document Code： A  Article ID： 1671-7988（2020）18-16-06

前言

在無人驾驶领域中 轨迹规划有多种算法 主要分为：1）基于搜索的规划算法 如：Hybrid A 算法、DLite算法;2） 基于采样的规划算法 如概率路线图（PRM）和快速搜索随机树（RRT）算法;3）人工势场法;4）参数化曲线构造法。本文中循迹路径算法即采样的参数化曲线构造方法实现的。

参数化曲线构造法又分为多项式曲线 贝塞尔曲线样条曲线和Dubins（直线和圆弧）。Andrei M Shke等人对dubins曲线进行了研究 对起始点的姿态进行了坐标变换 完成了各类情况的路线计算[1];刘流等研究了带速度约束的dubins路径 研究表明 拐弯半径是速度的函数 当速度较大时 需要匹配更大的转弯半径 并进行了无人机飞行验证[2];吴克风等人针对起终点距离较近情况 进行了不同情况下的分类 推导了并验证了各类情况下的最短路径情况[3];杨秀霞等人 考虑了角度约束 即起始转弯半径不同情况下的路径 并对不同角度下的路径进行了分析对比[4]。黄得刚等人，研究了三维Dubins路径 即在位置中加入不同的高度z 其核心主要是对起终点不同高度进行插值 并对三维Dubins路径进行了仿真实验[5]。

目前基于倒车和起始点转弯半径（曲率）不同的Dubins路径研究较少 而加入倒车模式会得到更短的路径并在某些特定的领域如避障 自动泊车等方面大有所为。本文研究了加入倒车和选择不同的起始转弯半径情况下的Dubins路径 算法另辟蹊径 解决了车辆循迹路径生成问题。

1 问题描述

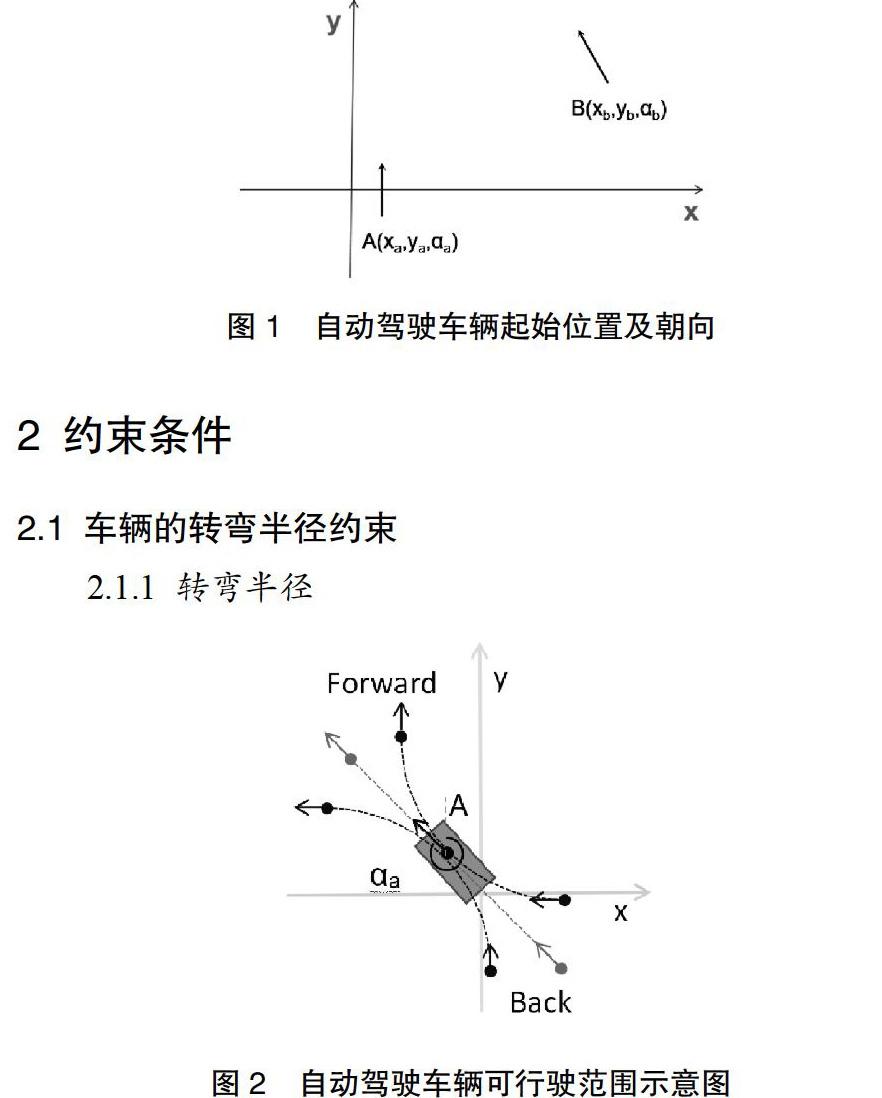
在一个二维平面中 寻找两个带方向的点间的最短光滑路径。起点为A（xa，ya） A点头车朝向为αa 车头朝向与地理方位角一致 即正北为0度 范围为[0-360];终点为B（xb，yb） 终点车头朝向为αb。寻找从起点A到终点B的最短光滑路径。车辆的转弯半径设置为R 受车辆最小转弯半径约束 R选取应大于车的最小转弯半径。

2 约束条件

2.1 车辆的转弯半径约束

2.1.1 转弯半径

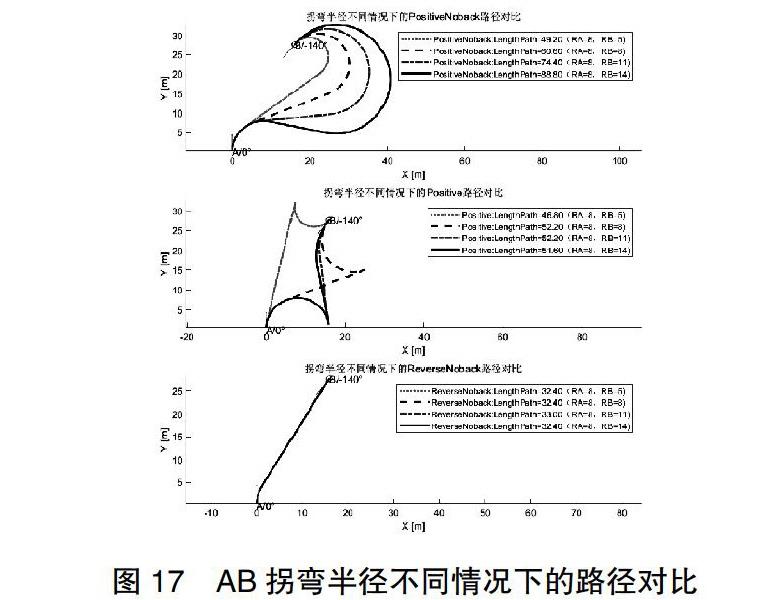
由于车辆的结构特征存在最小拐弯半径 有些车辆的左转最小拐弯半径和右转最小转弯半径还可能不相同 如图2所示 已知A点的位置及方位角αa 由一个特定的位置出发 车辆在下一步只能到达它可能到达的位置 受制于汽车最大转弯半径的限制。下图中红色箭头表示车辆在最大拐弯半径情况下的极限可行驶方向 蓝色表示直行。车辆前方区域表示正向行驶的区域 范围为极限右转与极限左转之间;车辆后方为倒车情况下的可行驶区域;范围也为为极限右转与极限左转之间。那么只要给定车辆的拐弯半径大于车辆的极限拐弯半径 车辆是可以行驶的。

2.1.2 实车转弯半径参数

本次实验采用的是传祺GE3改装的自动驾驶车辆 最大拐弯半径根据实车采集数据获取如图3所示 车辆的左转和右转情况具有不同的最大转弯半径 左转最大转弯半径为3.75m 右转最大转弯半径为4.2m。

2.2 倒车约束约束

如下图所示 在某些情况下 正向行驶会走更长的路程 例如终点在起点的正后方 且车头朝向和初始车头朝向一致 这样车辆只需挂倒挡即可实现到达终点。又如当车辆从A点出发 通过固定的拐弯半径可以实现到达终点B且满足到达B的车头朝向 同时车辆也可以挂倒挡实现到达终点B且满足B点车头朝向。对比发现 挂倒挡走的路径要远小于前进走的道路。因此对于任意车辆可走的圆弧 均有两种到达方式 一种时正向行驶 一种是后退行驶 走的弧段大于半圆称之为劣弧 走的弧段小于半圆称之为优弧。因此车辆在加入倒车模式后 在某些情况下能够得到更短的路径。

文中以f（forward）表示向前行驶 以b（back）表示倒车行驶 故对应于直线情况 将AB直线记为 前进直线路径记为 倒车直线路径记为。对于圆弧路径情况 将起终点圆弧记为 那么向前行驶弧AB记为 倒车行驶AB记为。

3 算法实现

3.1 算法构思

对于任意位置任意车头朝向的两个起终车位点 无论情况怎样复杂都可以将其划分为如图四种情况 即考虑实际情况 车辆可以左转出发也可以右转出发 到达终点可以是左转到达或者右转到达。

假设在不考虑避障及车辆速度情况下 认为在任意位置车辆都可以按车头反方向倒车行驶。

实际路线为车辆从起点A以拐弯半径R走圆弧（向左或向右） 接着直行走起终点两个圆弧的公切线 最后以拐弯半径R走圆弧到达终点B 即路线为圆弧-直线-圆弧路线。可将所有情况都列出 最后对到达终点过程中是否有倒車情形及到达终点车头的正反向情况进行分类。将行驶过程中有无倒车状态记为'Back'或者'Noback';将到达终点B与目标车头朝向的正反状态记为'Positive' 'Reverse';那么所有状态可以为：'PositiveNoback' 'PositiveBack' 'ReverseNoback' 'Reverse Back'四种。四种状态分别表示为：到达终点正向且行驶中无倒车情形;到达终点正向且行驶中有倒车情形;到达终点反向且行驶中无倒车情形;到达终点反向且行驶中有倒车情形。编写算法计算求出所有存在的路径 并对路径的状态进行标注。

编写选择路径算法 一般情况下 更为关心的是行驶过程中无倒车情形且到达终点B头车朝向一致的路径。选择最短的作为最终需求的路径。最后按需提取不同状态路径即实现了路径的生成。

3.2 路线说明

3.2.1 基础路径

以图5左上图（从起点A右边出发 左边到达终点B情形）为例进行说明 从A到B有4种路线 分别是黄色 绿色 蓝色 紫色四种路径。1.黄色路径为（圆弧 直线 圆弧）;2.绿色路径为（圆弧 直线 圆弧）;3.蓝色路径为（圆弧 直线 圆弧）;4.紫色路径为（圆弧 直线 圆弧）。

3.2.2 实际车辆行驶路径

根据圆弧的可正向行驶和反向行驶的特征 到达一个圆弧处的终点B有两种方式到达 根据上述路线需要走两个圆弧 故每一条路线 可以有四种行驶方法。具体以图6为例黄色路线为例进行说明车辆可能行驶路径为①（）②（）③（ ）④（ ）。

3.2.3 路径状态标注

对图6路径进行分析可以发现该路线到达终点B的车头朝向与需求的正好相反 其中只有路径①没有倒车行驶情况。那么路径①的状态为'ReverseNoback' 其他的路径状态为'ReverseBack'。图5中第一种情况路径状态见表1 其它三类情况类似 均可求出每条路径的状态 故其他三类情况不在赘述。

3.3 算法实现步骤

3.3.1 求圆心

以A点为例 输入为（xa，ya，αa）及拐弯半径R 可以求得左右共两个圆的圆心位置。输出为圆心CA（xi，yi）（i=1，2） 同样终点B处可以求取两个圆心CB（xj，yj）（j=1，2）。

式中 x y为圆心的横纵坐标;xa ya为起点的横纵坐标位置;αa为起点车头朝向;中+表示右侧圆心位置的求法 -表示左侧圆心位置的求法。

3.3.2 求两圆公切点

根据两圆相切公切线存在情况 如图7 当两个圆的半径相同时存在四种情况即：有四组公切线（两圆相离） 三组公切线（两圆外切） 两组公切线（两圆相交） 没有公切线（同心圆 即两圆重合）。

求取两个圆相切的所有切点对。输入参数为CA（xCA  yCA） RA CB（xCB yCB） RB;输出参数为公切点对 即两个切点组成的切点对 如图8所示外公切线中的切点对[A1，B1] [A4，B4]及内公切线中的切点对[A2，B2] [A4，B4]。计算公式如下：

3.3.3 路径生成

只需将圆弧或者直线路径求出 按照圆弧-直线-圆弧路线生成轨迹路径即可 三段路径可用相同的算法进行编写。输入参数为：起点位置及车头朝向A（xa，ya，αa） 终点位置A1（xa1，ya1） 向前或者向后行驶（forwardorback） 输出为终点车头朝向αa1 路径长度dAA1 离散路径序列点 （xi，yi，αi）。由于路径为离散采样 可以根据不同的需求进行设计 如等长度分割 等数量分割等。算法实现详细如下图所示。

4 算法仿真结果

4.1 路径展示

4.1.1 路径情形展示

对于任意位置 任意车头朝向的两个起终点 根据图5所示 一种情况最多有16组路径 4种情况共计最多有64种解。例如A点（0，0，0） B（15，15，315） 拐弯半径R=5。如图所示为存在64组解的所有情况。具体路径图见图10-13。

4.1.2 路径分类统计

根据展示的所有路径 对路径分类统计结果如下表所示。

4.2 路径筛选结果对比

选择符合要求的路径进行分析显示 一般情况下 更关注正向的没有倒挡情况下的路径即'PositiveNoback' 此外在有倒车情形下的最短路径'Positive'也是非常关注的 下面通过不同的参数对比两者路径中的最短路径。

4.2.1 转弯半径相同时 各类情况路径对比

（1）对比AB直线距离不同情况下的路径;设置起点A位置为（0，0，0） 车的拐弯半径R=8 设置起终点车头朝向αb=60° B点与A点距离分别为0 R 2R 3R情况下的路径对比如下。

（2）B点与A点距离固定B点的车头朝向不同情况下的路径;设置起点A位置为（0，0，0） 车的拐弯半径R=8 设置起终点B在A的某个象限 B点车头朝向不同情况下的路径对比如下。

（3）B点与A点距离固定 B点车头朝向固定 B位于A不同象限情况下的路径。设置起点A位置为（0，0，0） 车的拐弯半径R=8 设置起终点车头朝向αb=60° B点分别位于A的不同象限情况下的路径对比如下。

综合对比可以得出：算法可以找到任意复杂情况的最短路径;加入倒车情形会得到更短的路径。

4.2.2 转弯半径不同时 不同类别路径对比

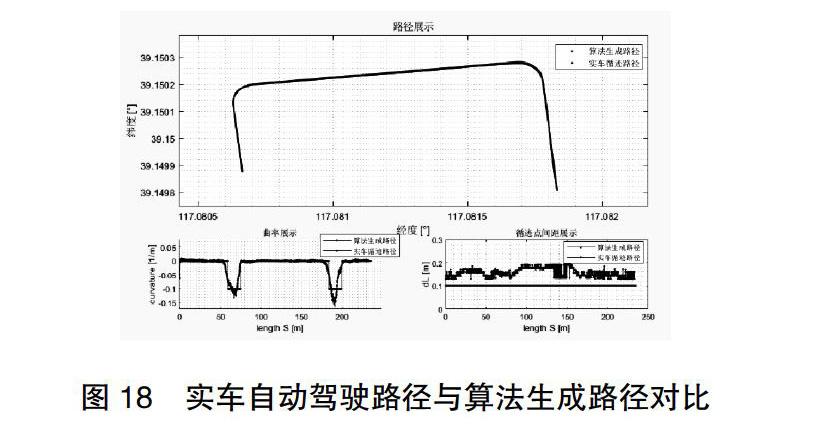
设置起点A位置为（0，0，0） 车的起始拐弯半径RA=8 设置起终点B位置为（0，0，0） 到达B点拐弯半径分别设置为RB=[5，8，11，14] 三种不同类型（'PositiveNoback';'Positive';' ReverseNoback'）情况下的路径对比如下。

4.2.3 结论

对比曲线可以得出以下结论。1、不同转弯半径约束下 半径越大会得到更长的路径里程;2、加入倒挡模式在某种情况下会得到更短的路径 倒车路径的影响范围比没有倒车情况更小 倒车路径的控制复杂度要高于没有倒车情形的路径;3、所有路径中存在到达B点但与预期的车头朝向相反的路径 且在某些情况下会有更短的路径 当某些场合不太关注车头的正反向时有重要意义。

5 实车验证

通过仿真结果可以给出任意情况下 起终点的连接路径 算法在自动驾驶场地进行了实车测试 对比结果如下图：

根据路径展示情况可以看出 实车循迹路线与算法生成的路线基本吻合 仅在拐弯处存在一定的误差;分析曲率变化情况可以看出 算法生成的曲率平滑 当曲率为0表示直行 曲率为-0.1表示车辆以拐弯半径为10m进行左转 实车循迹路线的曲率为缓慢增大再变为0 这是由于车辆控制算法导致的 车辆完成左转首先需要逐步左打方向盘 待完成拐弯后方向盘回正 表现出来的是曲率的绝对值先增大后减小;点距为采样点 算法生成的路线点是10cm一个点 实车采样点距为10cm～20cm之间。

通过实车实验 验证了算法的可行性 大大提高了无人驾驶车辆的测试效率 解决了要进行测试首先需要车辆去录制轨迹数据这一“痛点” 在实践中得到广泛应用。

最后算法在车辆远程控制中得到应用 将算法集成在web端 通过远程路径下发来控制无人驾驶车辆自动驾驶至目的地。

6 结束语

本文通过详细介绍了自动驾驶循迹路线生成算法 通过该算法生成的路径可指导自动驾驶车辆按照路径进行自动驾驶。解决了自动驾驶车辆必须先录制车辆轨迹路径才能进行自动驾驶的弊端。极大的提升了控制的灵活性。

通过实车进行了测试 在空旷的无人驾驶场地中自动驾驶车辆按照算法生成的既定路线进行自动驾驶。

参考文献

[1] Andrei M Shkel，Vladimir Lumelsky. Classification of Dubins set[J]. Robotics and Autonomous Systems 2001，34，179-202.

[2] 刘 流，梁晓龙，何吕龙，等.考虑速度约束的无人机Dubins路径规划[J].火力与指挥控制，2018，43（12）：50-58.

[3] 吴克风，曹晓文，周其忠，等.任意距离下Dubins最短路径研究[J].战术导弹技术，2017，1：76-84.

[4] 杨秀霞，曹唯一，张毅.时间和角度约束下的双圆弧路径规划[J].空间控制技术与应用，2019，41（8）：1835-1843.

[5] 黃得刚，章卫国，杨立本.无动力无人机进场阶段三维Dubins路径跟踪方法[J].系统工程与电子技术，2016，38（3）：629-637.