零弯矩增量法在拱桥拱轴线优化中的应用
2020-10-28张家琪
张家琪,李 威
(长沙理工大学土木工程学院 长沙410002)
0 引言
拱结构与梁结构相比,拱结构最显著的特点是在承受竖向荷载时,拱脚处会产生水平推力,该水平推力产生的弯矩可抵消由拱上荷载产生的弯矩。当拱轴线与拱圈荷载压力线重合时,拱圈内只有轴力,而无弯矩和剪力,此时的拱轴线称为合理拱轴线[1]。但在实际工程中,拱圈受恒载、活载、温度变化、地基沉降和材料收缩等多种作用影响,这其中,除恒载外,其余的荷载均是不确定的,因此合理拱轴线也无法唯一确定。考虑到拱桥,特别是大跨度拱桥,其恒荷载在所有荷载中所占比重较大,因此一般可用恒载压力线作为合理拱轴线,优化过程中就是拱轴线不断地逼近恒载压力线的过程。针对这一目标,国内外学者进行了许多研究[2-5],且形成了四次样条函数法[6]、三次样条差值法[7]、加权能量方法[8]等多种优化计算方法,且都能较好地实现拱轴线向合理拱轴线的逼近。
1 零弯矩增量法及拱轴线拟合
1.1 基本假定
⑴拱上建筑的结构状态不因拱轴线的变化而变化,即拱圈上荷载不变。
⑵只考虑拱圈和拱上建筑的自重恒载作用。
1.2 零弯矩增量法和曲线拟合
1.2.1 拱轴线离散
拱轴线离散时选取立柱与拱圈连接点作为分段划分点,若拱上建筑主梁跨径较大或存在主梁不等跨布置时,可在两立柱中间添加分段划分点,保证离散结果的准确和后期迭代收敛的精度,因拱圈为对称结构,取半跨计算,如图1所示。实际工程中拱轴线多采用“五点重合法”[9]或多次抛物线确定,以某一较合理的拱轴线建立有限元模型,提取各分段划分点处的剪力和轴力和拱圈各节点的初始坐标。
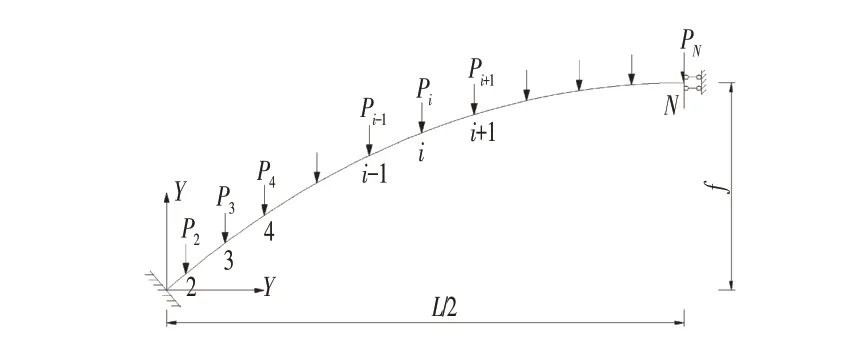
图1 半跨拱圈计算示意图Fig.1 Half-span Arch Circle Calculation Diagram
1.2.2 计算拱圈各离散点纵坐标增量
以初始拱轴线建立有限元模型,提取各分段节点处的轴力N和剪力V以及各分段轴线与水平线的夹角θ ,通过改变分段较高端点的纵坐标,使该分段在轴力N和剪力V作用下由较高端点到较低端点的弯矩增量为0,以此得到分段端点的纵坐标调整量。若分段数为n,任取一个分段为例,计算图示如图2所示。
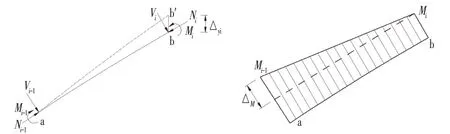
图2 拱圈分段内力与弯矩示意图Fig.2 Diagram of Internal Force and Bending Moment of Arch Ring Segment

其中i∈[1,n],且i为整数。
求得所有离散分段的节点纵坐标增量后,为保证拱圈线形的连续,计入各离散点纵坐标增量的叠加效应,则拱圈各离散点纵坐标增量为:
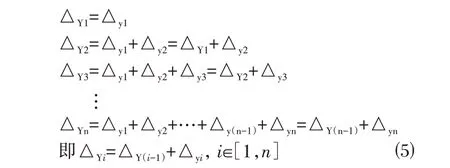
1.2.3 迭代计算各节点纵坐标
拱圈线形变化会造成拱圈内力和各分段轴线与水平线夹角的改变,所以以初始拱轴线建立有限元模型后,需计算出拱圈各离散点的初始内力以及各分段轴线与水平线的夹角,并按式⑷、⑸进行迭代计算,每计算一次都要输出拱圈各离散点的内力以及各分段轴线与水平线的夹角,作为下次迭代计算参数,直至拱圈弯矩满足以下迭代终止条件[10]。
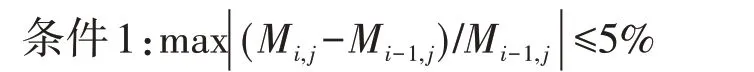
式中:Mi,j为迭代第i次时第j号离散点弯矩;Mi-1,j为迭代第i-1次时第j号离散点弯矩。
当满足该条件时,可认为拱圈受力已趋于稳定。
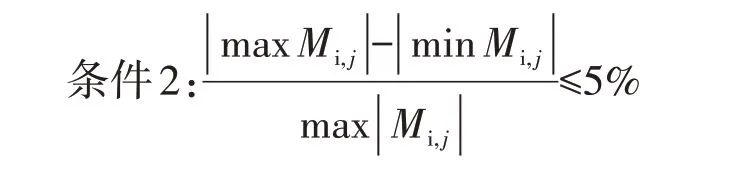
当满足该条件时,可认为当前拱圈线形,弯矩内力趋于均匀。
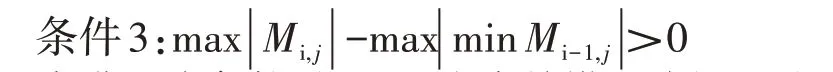
当满足该条件时,可认为当前拱圈线性的改变不利于拱圈的受力,拱轴线与恒载压力线产生了更大的偏离,此时以第i-1次的迭代结果作为最终的优化线形。
1.2.4 高次抛物线拟合
通过迭代计算所得的各离散点可以较好逼近拱圈恒载压力线,但根据这些离散点绘制的拱轴线是一条不规则曲线,该拱轴线不能用明确的方法进行表示,实际工程中的施工放样也不便进行。这类问题可通过曲线拟合进行解决,通过高次抛物线的拟合,将离散的数据点建立数据关系(数学模型),使优化后的拱轴线的实际应用性得到提高。
2 零弯矩增量法拱轴线优化流程(见图3)
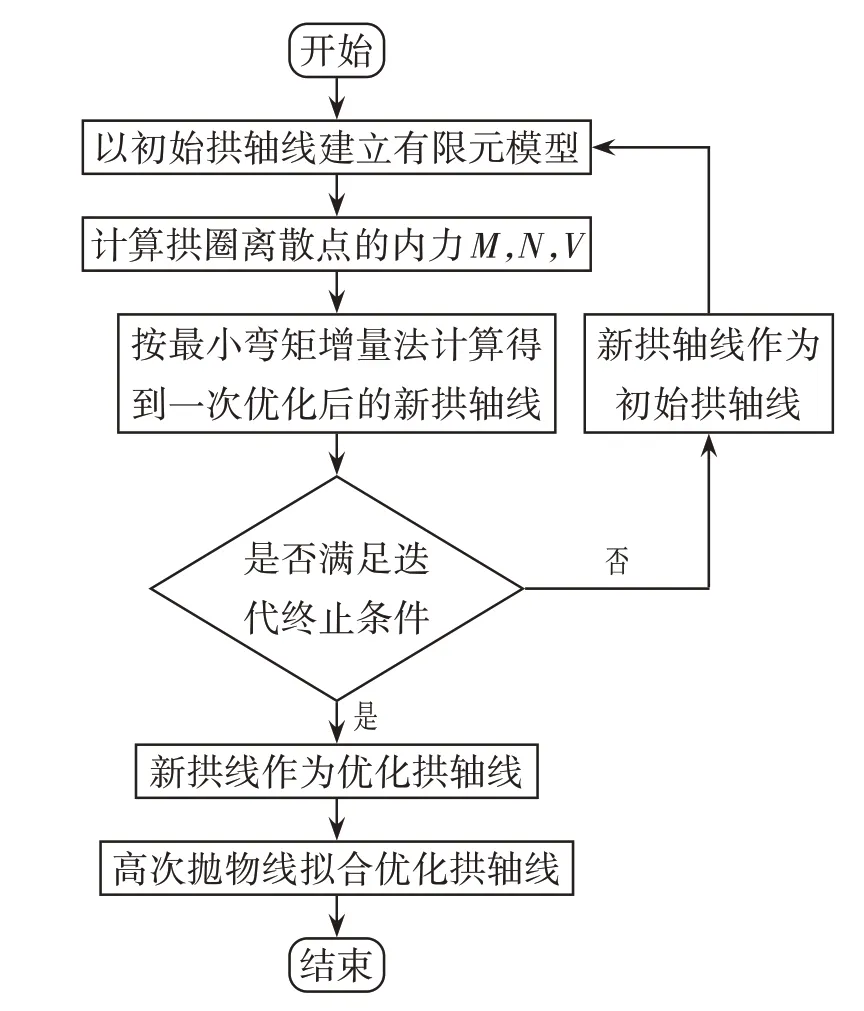
图3 零弯矩增量法优化流程Fig.3 Optimization Flowchart of Zero Bending Moment Incremental Method
3 算例
某特大桥主拱圈为计算跨径197.356 m 的无铰箱型拱。矢跨比为1/5,拱轴线为悬链线,按拱顶、1/4 跨径及拱脚截面重合为条件,拱轴系数m=1.543。将半跨拱圈轴线离散为11 个分段,拱轴系数m=1.543的拱轴线为初始拱轴线,初始拱轴线12个离散点的纵坐标为Y0,采用零弯矩增量法优化后的拱轴线离散点纵坐标为Y,优化拱轴线拟合为4 次抛物线所得拱轴线,其离散点的纵坐标为Y4。各拱轴线坐标如表1 所示,线形如图4所示。

图6 拱圈弯矩对比Fig.6 Arch Ring Bending Moment Comparison Chart
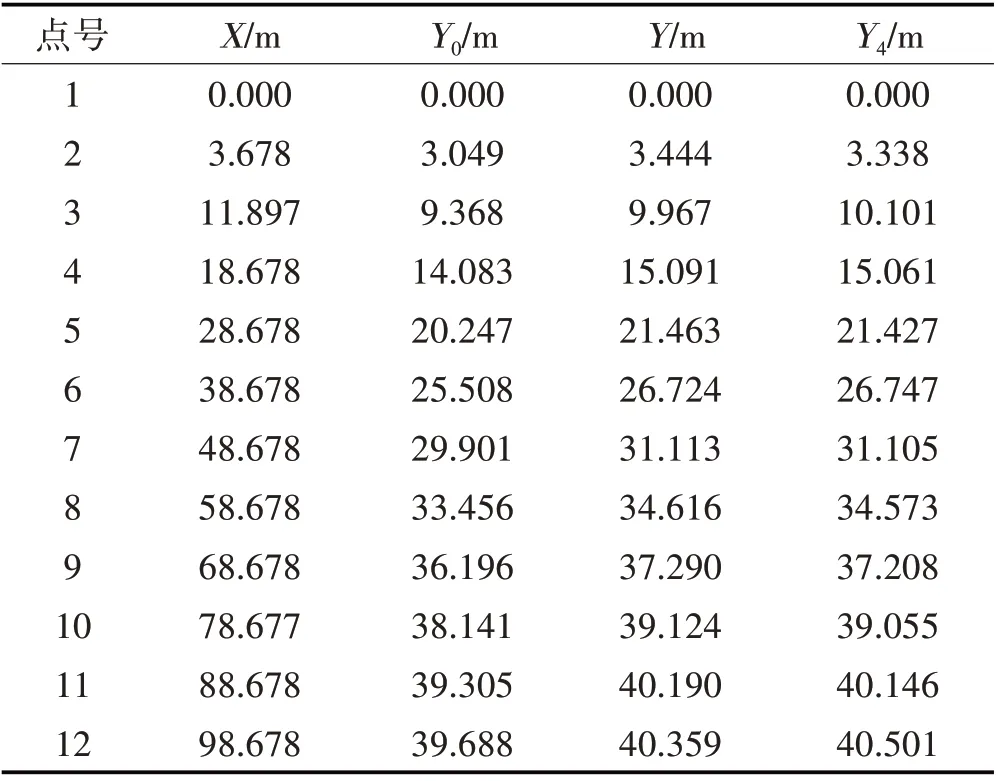
表1 拱圈离散点在各线形中的坐标Tab.1 The Coordinates of the Discrete Points of the Arch Ring in Each Line
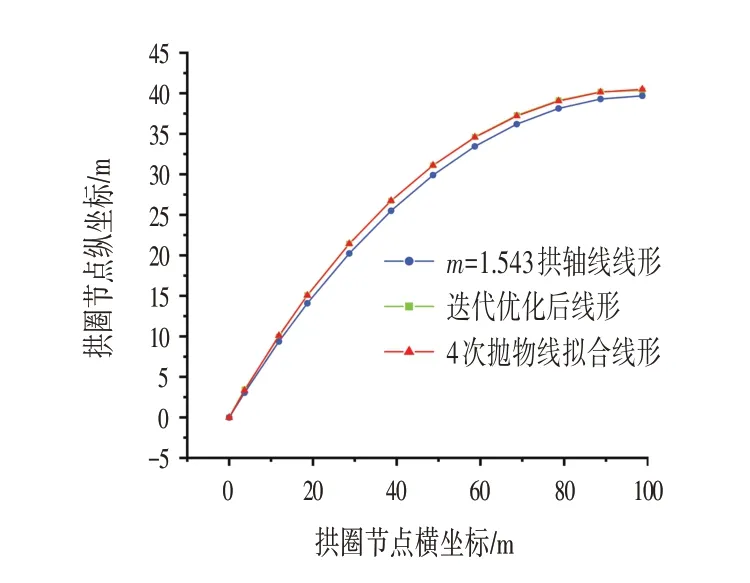
图4 拱圈线形关系Fig.4 Arch Circle Linear Relationship
设计拱轴线方程为:
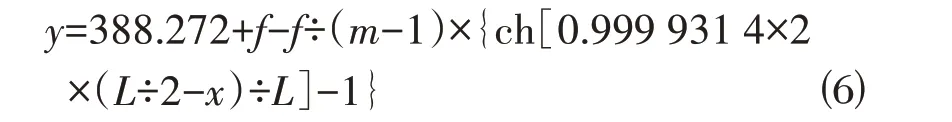
式中:f 为拱圈失高(m);L 为拱圈计算跨径(m);m 为拱轴系数。
优化拱轴线拟合为4次抛物线为:
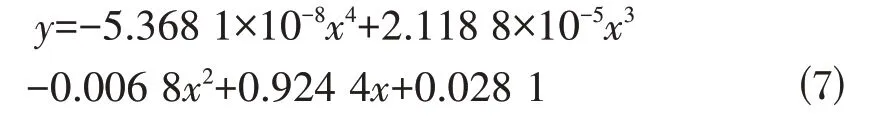
以各拱轴线建立该特大桥有限元模型,有限元模型(以初始拱轴线为例)如图5所示。在成桥恒荷载作用下,各拱轴线对应的拱圈弯矩如图6所示。
各拱轴线对应拱圈最小和最大弯矩如表2所示。

图5 某特大桥有限元模型Fig.5 Finite Element Model of a Bridge

表2 各拱轴线下最小及最大弯矩Tab.2 Minimum and Maximum Bending Moments under Each Arch Axis
实例计算结果表明,采用零弯矩增量法迭代优化后,拱圈内力趋于均匀、最大弯矩值明显降低;采用4次抛物线拟合后拱轴线在成桥恒载作用下,最大弯矩比初始拱轴线在该荷载作用下的最大弯矩减小了62%。
4 结论
⑴零弯矩增量法可较好地实现拱轴线向恒载压力线即合理拱轴线的逼近,通过计算和实例表明,经过该方法优化后,拱圈弯矩大幅减小且趋于均匀,其中拱脚位置处的弯矩优化效果较明显。
⑵通过对拱上建筑建立有限元模型来实现拱上荷载的精确模拟。这一点体现在即使是主梁采用简直支体系,因拱圈承受荷载后发生变形,拱上立柱内仍会有一定的弯矩产生,并传递至主拱圈。
⑶在成桥恒载作用下,4次抛物线拟合后拱轴线和迭代优化后拱轴线的内力状态存在一定偏离,宜采用更高次抛物线或差值函数进行拟合,对比寻求拟合最优解。
