200 GeV能量下d-Au碰撞系统中轻强子和夸克化学势的中心度依赖
2020-10-28卫华荣何兴伟洪碧海朱维婷刘陈翔朱德禹
卫华荣,何兴伟,洪碧海,朱维婷,刘陈翔,朱德禹,沈 鹏
(1.丽水学院工学院,浙江丽水323000;2.山西大学理论物理研究所,山西太原030006)
0 引言
虽然高能碰撞过程经历的时间很短,但是环境温度极高、密度极大,演化过程很复杂[1-3]。通常可通过分析系统产生的末态粒子的性质和产生机制来反推其复杂的演化过程。反应系统经过化学冻结和动力学冻结之后,产生的末态粒子的动力学性质也会被冻结,其横动量不再改变[4-5]。通过分析粒子的横动量分布,可以探索粒子的产生机制和系统的演化性质。唯象模型法是分析粒子横动量分布的一种简单而实用的方法。多源热模型[6-8]框架下的多组分厄兰(Erlang)分布[9]不但可以分析碰撞系统的横向激发程度、软硬激发过程贡献份额比,而且还可以提取到反正粒子产额比等信息。
在高能碰撞系统中,粒子的化学势是一个很重要的物理量,因为它决定着物质传递的方向和限度,是判断系统是否经历过相变、是否达到相平衡的重要依据。尤其是重子化学势,结合化学冻结温度,可以在化学冻结温度-重子化学势平面上研究强子物质到夸克物质的相变问题,进而分析QCD相图[10-11]。不同尺寸的碰撞系统产生的粒子的化学势是不同的。在之前的工作中[12],我们已经分析了金-金、铅-铅重离子碰撞系统和质子-质子轻离子碰撞系统中的粒子化学势,介于以上两种系统的氘-金(d-Au)系统,其产生的粒子的化学势有什么不同之处,引起了我们强烈的兴趣。粒子的化学势可以通过反正粒子的产额比[13]来获得,而反正粒子的产额比可以通过描述粒子横动量分布过程中提取的归一化常数来获得。通过归一化常数获得产额比的好处在于所考虑的横动量范围比较广,因而获得的产额比的值相对比较准确。
本文在多源热模型框架[6-8]下,利用双组分厄兰分布研究了200 GeV能量下d-Au系统中产生的几种末态粒子的横动量分布,根据提取的归一化常数得到了3种反正粒子的产额比(kπ、kK和kp),进而提取到了几种轻强子(π、K和p)和轻夸克(u、d和s)的化学势,并分析了化学势对碰撞中心度的依赖关系。
1 模型和公式
根据我们的理论,要得到归一化常数,首先需要对末态粒子的横动量分布进行描述。本文采用的模型是基于多源热模型[6-8]的多组分厄兰分布[9]。该模型假设高能碰撞中形成了多个发射源,这些发射源根据碰撞系统中不同的作用机制和实验测量过程中不同的样本条件可以分成多个组分。假设每组所有的发射源具有相同的激发度并处于共同的平衡或局域平衡态,则每组所有源贡献的结果可以用一组分厄兰分布进行描述。若粒子的末态分布是由两组发射源产生的结果,则可用双组分厄兰分布进行描述。
根据热力学理论,每个发射源产生的粒子的横动量分布服从指数分布,即:

其中,ptij表示第j组第i个发射源的横动量,〈ptij〉是ptij的平均值。若将第j组发射源的数目记为mj,mj个发射源产生的粒子的横动量记为pT,则第j组所有发射源产生的粒子的横动量分布就是每个发射源指数分布函数的卷积:
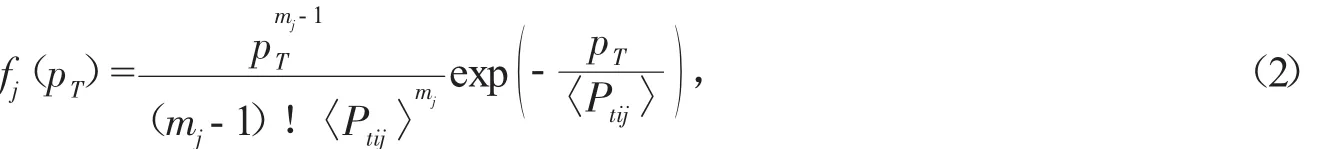
这就是归一化的Erlang分布。所有组发射源整体贡献的结果可以表示为:

其中,kj是指第j组发射源贡献的权重系数,且满足归一化条件,这就是多组分Erlang分布。
事实上,本文采用的是双组分的厄兰分布,第一组分反映的是发射源的软激发过程,第二组分反映的是发射源的硬散射过程。软激发过程对应低横动量区,硬散射过程对应高横动量区。
通过以上描述可以得到归一化常数,基于归一化常数可以获得反粒子-粒子的产额比,根据反正粒子产额比可以提取到粒子的化学势。需要注意的是,实验上由于包含顶夸克的粒子的寿命太短而无法测量,导致本文采集到的数据有限,所以只计算了一些轻强子(π、K和p)和一些轻夸克(u、d和s)的化学势。提取粒子化学势的原理如下。
根据热力学统计模型[13]中关于化学势和热力学平衡的统计学原理,可以得到反正粒子产额比和粒子化学势之间的关系:

其中,kπ、kK和 kp分别表示反粒子 π-、K-、与粒子 π+、K+、p的产额比,μπ、μK和 μp分别表示 π、K 和 p 的化学势,Tch表示反应系统的化学冻结温度。根据服从标准麦克斯韦-玻尔兹曼统计的非相互作用气体的统计热模型[14-15],该温度可由以下公式给出:
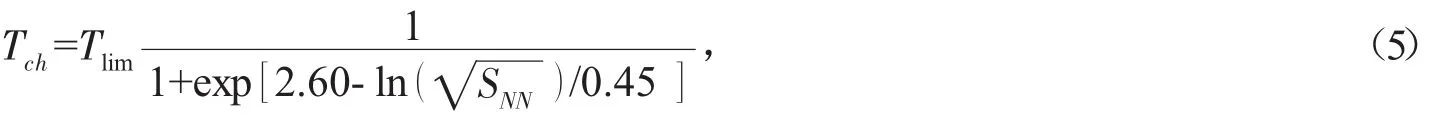
这里的“极限”温度Tlim可以取0.164 GeV,质心能量的单位为GeV。
假设 μu、μd、μs分别表示 u、d、s夸克的化学势,根据公式(4)和文献[16-17],随夸克化学势变化的产额比可以表示为:
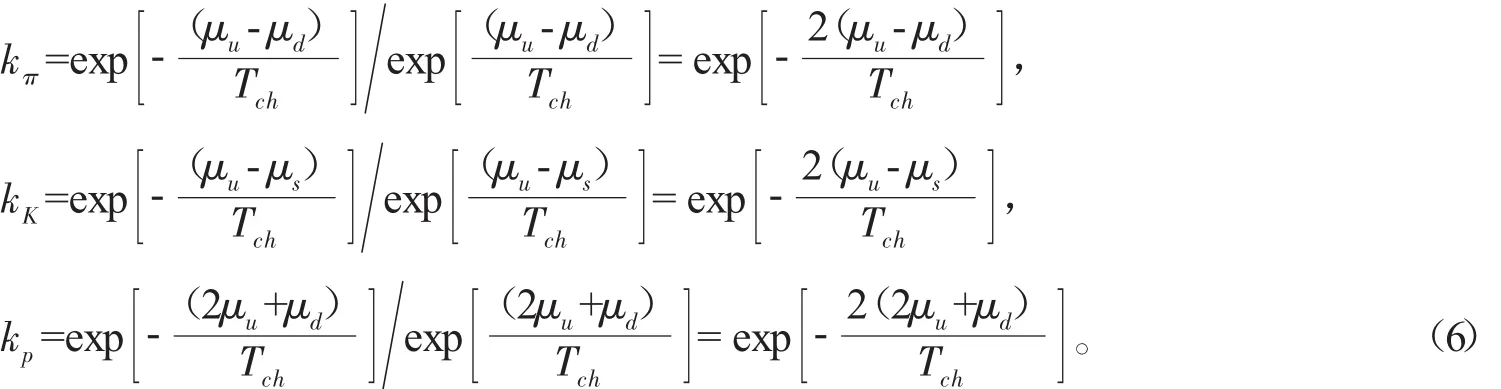
根据公式(4)和(6),强子和夸克的化学势可以分别表达为:

和
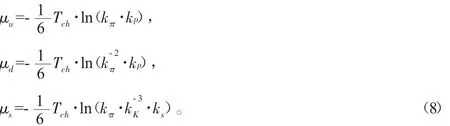
2 结果分析和讨论
图1显示的是d-Au系统在质心能量200 GeV下不同中心度区 (0%~20%、20%~40%、40%~60%和60%~88%)碰撞产生的(a)(d)π±、(b)(e)K±、(c)p 和(f)的横动量分布。实验数据是由PHENIX合作组[18]测量的。不同中心度区的数据用不同形状的符号表示在图中。为了更清晰地区分出不同中心度区的数据,各组数据根据图中标识的倍数被相应缩小了。图中数据点上的误差棒包含了统计和系统误差。实验点上面的实线是根据双组分厄兰分布拟合的结果,对应曲线的自由参数(m1、〈pti1〉、k1、m2、〈pti2〉),归一化常数(N0)和χ2每自由度(χ2/dof)的取值列在了表1中。可以看出,双组分的厄兰分布可以很好地描述实验数据。不同粒子对应的发射源的软激发度权重系数k1均大于60%,表明软激发是主要的激发过程。对于质子和反质子,由于其产生过程方式很多,导致提取的软激发的贡献份额偏低,但是跟硬散射过程相比,其依然是主要的贡献者。对应低横动量区的第一组分的源数m1的值是2或5,表明低横动量的粒子来自2个或5个海夸克和胶子之间的相互作用;对应高横动量区的第二组分的源数m2的值都是2,表明高横动量的粒子来自两个价夸克之间更猛烈的迎头碰撞。
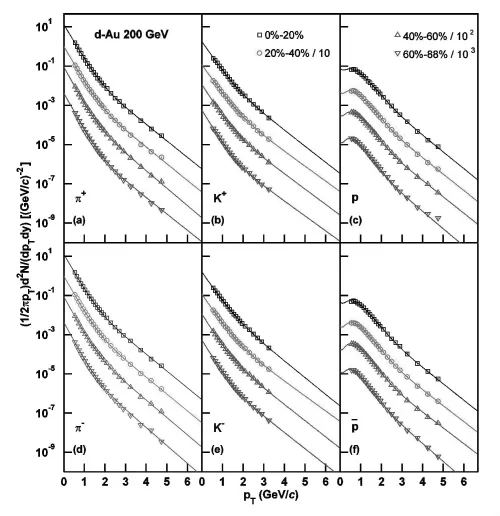
图1 质心能量200 GeV下d-Au系统在不同中心度区(0%~20%、20%~40%、40%~60%和60%~88%)碰撞产生的(a)(d)π±、(b)(e)K±、(c)p 和(f)的横动量谱。图中不同形状的符号表示的是PHENIX合作组测量的实验数据。为了看起来图像更清晰,不同中心度区的数据根据图中的倍数被相应缩小了。数据点上的误差棒包含了统计和系统误差。曲线是根据双组分厄兰分布计算的结果
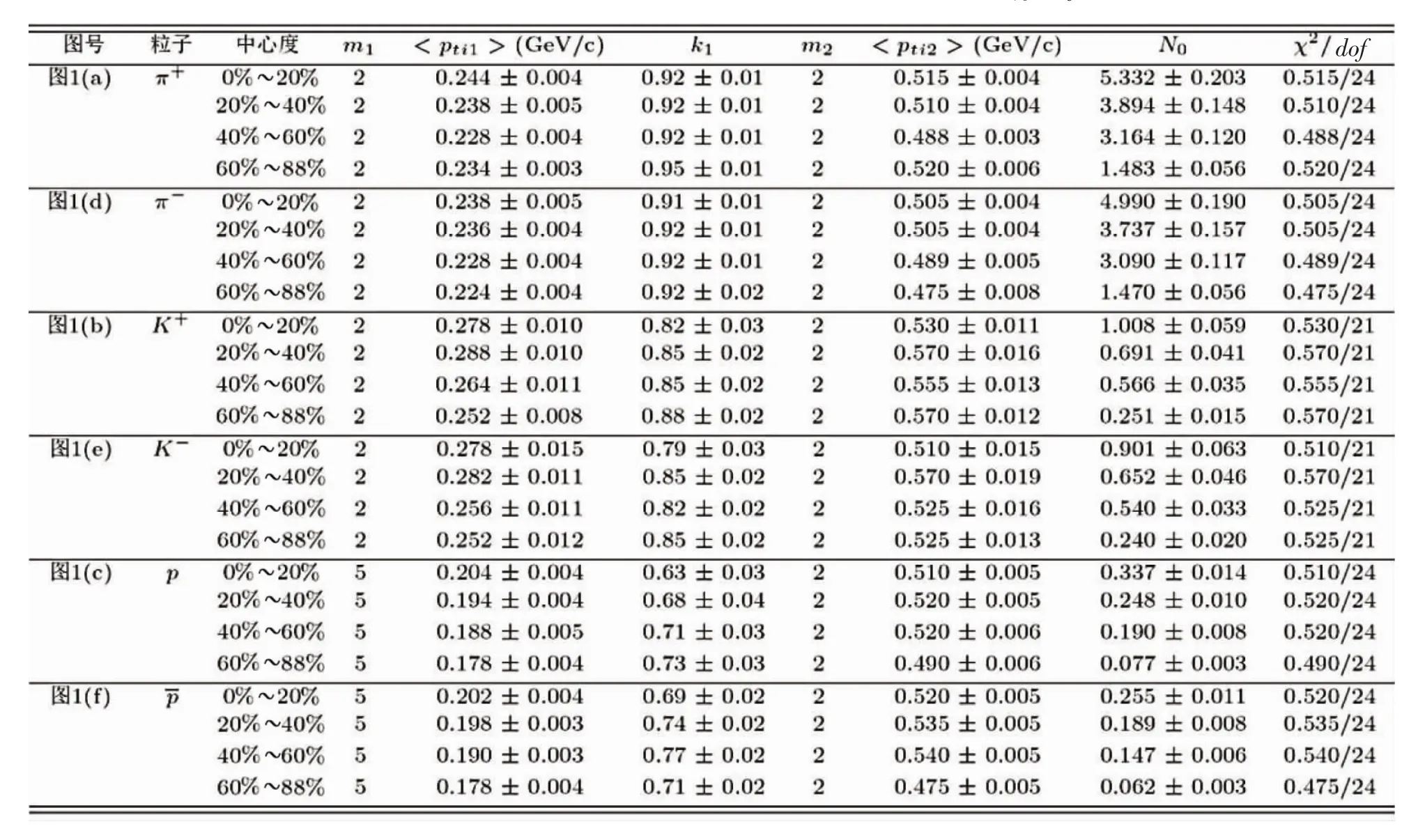
表1 图1中双组分厄兰分布曲线对应的自由参数、归一化常数和χ2/dof的值
根据以上描述和提取到的归一化常数,我们提取到了横动量和中心度依赖的反正粒子的产额比(kπ、kK和kp),其结果分别显示在图2和图3中。图2中的实线、虚线、点线和虚点线分别对应中心度区0%~20%、20%~40%、40%~60%和60%~88%的结果。可以看出,3种粒子产额比随横动量的变化在较小范围内波动,但无一致性的规律。换句话说,在误差范围内,3种轻粒子的产额比对横动量没有明显的依赖关系。对同一种粒子产额比,不同中心度区的产额比曲线也没有表现出明显的大小关系,说明横动量依赖的产额比对中心度的依赖性也不明显。图3显示的是3种粒子产额比对中心度的依赖关系。作为参考,图中分别给出了3种粒子产额比的平均值,kπ、kK和kp的平均值分别为0.966、0.937和0.775,并用3条虚线显示在了图中。可以看出3种粒子产额比随中心度区的增加有微小的增长趋势,但增长幅度不大,严格来讲,也可以认为,在误差范围内,3种产额比对中心度无明显的依赖关系。
基于以上粒子产额比和公式(7)(8),可以提取到中心度依赖的3种轻强子和3种轻夸克的化学势,其结果如图4所示。可以看出,在200 GeV能量下的d-Au系统中,6种粒子的化学势随中心度的变化较小,也可以说,在误差范围内,6种化学势对中心度没有明显的依赖关系。3种轻强子的化学势多数在20 MeV以下,3种夸克的化学势更小些,都在10 MeV以下,有些中心碰撞区的化学势甚至接近于0,这与之前的研究结果是一致的。另外,还可以看出,μp>μK>μπ、μu≈μd>μs,这是由于粒子的质量不同所造成的。
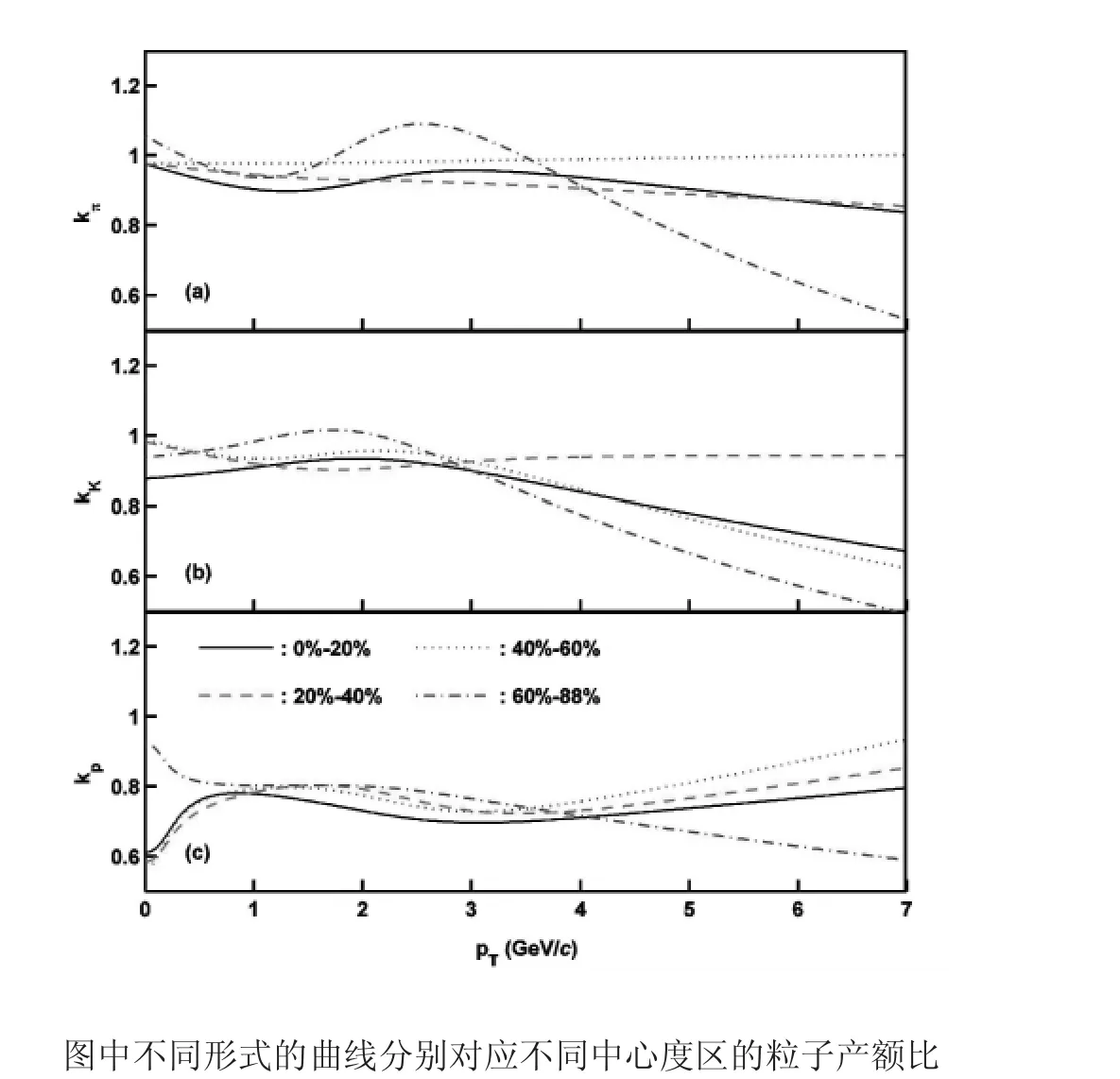
图2 3种粒子产额比对横动量的依赖关系
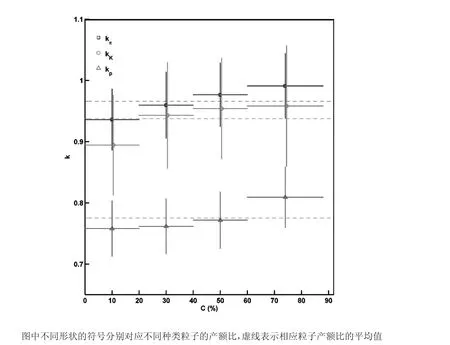
图3 3种粒子产额比对中心度(C)的依赖关系
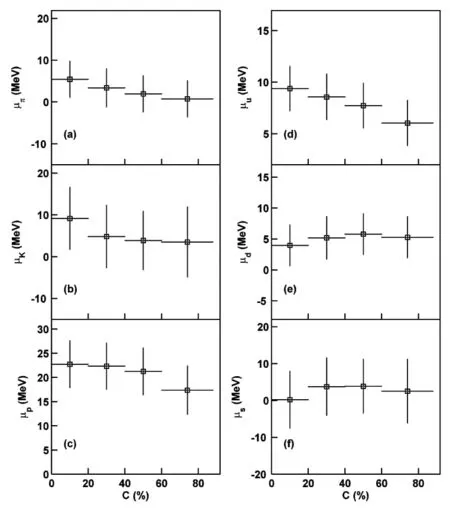
图4 3种轻强子和3种轻夸克的化学势对中心度(C)的依赖关系
3 结论
综上讨论,可得出以下几点主要结论:
(1)通过利用多源热模型框架下的双组分厄兰分布分析质心能量200 GeV下d-Au系统碰撞产生的π±、K±、p 和的横动量分布,可以看出,双组分厄兰分布可以很好地描述PHENIX合作组测量的实验数据。从拟合参数可以看出,末态粒子的横动量谱可以认为是由低横动量区和高横动量区两部分构成的,低横动量区粒子来自碰撞过程中几个海夸克和胶子之间相互作用引起的软激发过程,而高横动量区粒子则来自两个价夸克之间更加猛烈的迎头碰撞引起的硬散射过程。从权重比例看,软激发过程产生的粒子占比在60%以上,表明碰撞系统的横向激发程度主要由软激发过程贡献。
(2)根据拟合结果和拟合得到的归一化常数,可以提取到横动量和中心度依赖的3种轻强子(π、K和p)的反正粒子产额比。研究表明,200 GeV能量下d-Au碰撞系统中产生3种轻强子的产额比随横动量的增加变化较小,且没有一致性的规律,随中心度区的增加而轻微增加,但增加幅度较小。因此,也可以认为,在误差范围内,这3种产额比都没有表现出对横动量和中心度明显的依赖关系。基于以上反正粒子产额比,可以提取到随中心度变化的3种轻强子(π、K、p)和3种轻夸克(u、d、s)的化学势。研究表明,d-Au系统在200 GeV能量下碰撞产生的轻强子和夸克的化学势都比较小,随中心度区的增加变化幅度也比较小,也可以认为,在误差范围内,这6种化学势对中心度的依赖关系不明显。
