马马崖水电站溢流坝段三维深层抗滑稳定分析

赵 飞，范书立

(1.应急管理部国家减灾中心，北京 100124； 2.大连理工大学 水利工程学院，辽宁 大连 116023)

混凝土重力坝的抗滑稳定分析与安全评价是一个复杂的问题，尤其对重力坝的深层抗滑稳定，坝基内存在大量的节理、裂隙软弱面，这往往成为影响坝体安全的关键问题[1]。据不完全统计，我国已建、在建和设计中的大中型重力坝，地基内存在软弱夹层的重力坝达90多座。相对浅层抗滑问题来说，深层抗滑问题更为复杂，主要是软弱结构面勘察的困难性和抗剪断参数测定的复杂性，正是由于这些不确定因素的存在，导致精确分析重力坝深层滑动模式及安全性十分困难。因此，研究重力坝深层地基软弱结构面等地质缺陷对结构整体稳定性的影响具有一定的工程实际应用背景[2]。由于问题的复杂性，许多学者提出了各种分析方法，一般来说，重力坝深层抗滑稳定问题的计算分析方法包括刚体极限平衡法[3-5]、数值方法[6-8]以及模型试验法[9]等，核算的安全系数以整体安全度为主，辅以局部安全度的检查。目前国内外一般均按简化的平面刚体极限平衡方法计算。但是由于该方法假定滑移体为刚体，只考虑作用在滑移面上的法向力和切向力，不考虑弯矩作用，不能考虑滑体内部的互作用，也不能反映滑动面的三维特征，众多的假定和简化使得其计算结果与实际稳定状态存在一定的差别，计算精度依赖于所采用假定的合理性[3]。

有限元法应能够模拟基岩的地质构造以及软弱岩体的物理力学特征，使得坝体及滑动面的受力状态较接近实际，已经在大型水电工程设计中得到广泛应用[10-12]。相应的将有限元应力成果代入刚体极限平衡法中推求滑块稳定安全系数的强度校核法(应力代数和法)，因概念清晰且能得出工程中通常密切关注的安全系数也逐渐为广大工程技术人员所接受[13-14]。许多学者都对该方法的适用性进行了深入研究，并取得了重要的研究成果[15-16]。吴中如等[17]对采用有限元法计算大坝抗滑稳定的适用性进行了总结分析，认为对于重要的工程，特别是抗滑稳定问题较为严重时应采用有限元法进行验证。孙剑等[18]针对复杂地质条件上重力坝深层抗滑稳定问题，基于坝基应力场给出了滑裂面应力积分等安全系数法的力平衡方程，建立了组合滑裂面深层抗滑稳定计算模型。龚亚琦等[19]将有限元法和刚体极限平衡法相结合，根据有限元结果计算截面内力从而提取滑动力和抗滑力来计算深层抗滑稳定系数，确定了双滑面模型的关键参数。王毅[20]以车家坝河混凝土重力坝为研究对象，探讨了三维有限元计算重力坝抗滑稳定的可行性，研究发现其计算成果与规范公式计算结果的误差在-2.78%～3.61%以内。孙建生[21]构建了有限元应力和宏观极限平衡耦合计算模型，以期消除对重力坝深层复杂滑移面抗滑稳定计算认为假定因素的影响。以上研究成果极大促进了有限元法在坝基抗滑稳定分析中的应用及深层抗滑稳定计算理论的发展。

本文以马马崖一级水电站为研究对象，建立了该工程溢流坝段群的三维有限元模型，采用应力代数和法对其进行了三维深层抗滑稳定计算分析，研究了坝段之间粘聚力及河床上下游岩体对大坝抗滑稳定性的影响，并将计算结果和刚体极限平衡法的计算结果进行了对比分析，以期为复杂地基上重力坝的深层抗滑稳定分析及设计提供研究和技术参考。

1 应力代数和法基本原理

应力代数和法是基于有限元的极限平衡方法，通过计算求得应力场，将有限元应力成果转换到滑动面上，求出滑移面上的阻滑力和滑动力，再按刚体极限平衡法的方式确定安全系数。一般是按下式通过对整个滑动面进行加权处理得到整个滑动面的安全系数。

(1)

式中:ci、σi、τi、fi分别为单元的黏聚力、滑动面上的法向应力、切向应力及摩擦系数；li为单元上滑动面长度。

对于重力坝三维模型而言，参照刚体极限平衡法分析拱坝坝肩稳定计算方法，视坝体及其滑动岩体为一整体的滑动体，计算整个滑动体稳定情况。本文按照《混凝土拱坝设计规范》[22](SL 282—2003)计算坝肩抗滑稳定公式进行计算。

kc=(f1N1+f2N2+c1A1+c2A2)/T

(2)

式中:kc为抗滑安全系数；N为各垂直滑裂面的作用力；T为沿滑裂面的切向力；A为各计算滑裂面的面积；c为各滑裂面的抗剪断黏聚力；f为各个滑裂面的抗剪断摩擦系数。

2 工程概况及计算参数

2.1 工程概况

马马崖一级水电站是北盘江干流开发选定方案中的第9级，以发电为主，航运次之的综合开发效益的枢纽工程，是“西电东送”第二批开工的工程之一。大坝为碾压混凝土重力坝，最大坝高117 m，正常蓄水位585.00 m，相应库容为1.365亿m3，电站总装机容量540 MW，年发电量为15.92亿kW·h。

坝址区出露地层主要为三叠系中统及关岭组第2段第2层(T2g2-2)中厚层夹薄层灰岩、泥岩、泥灰岩和第3层(T2g2-2)中厚层夹薄层球粒状泥晶灰岩，以及杨柳井组第1段(T2y1)中厚层与薄层灰岩互层和第四系覆盖层。坝基T2y1地层属于BIII2类岩体，地层属于BIII1类岩体[23]。

2.2 滑移模式的分析与确定

溢流坝段区地质条件如图1所示，区域内岩层倾左岸略偏上游，岩层单斜，产状变化较小。溢流坝段区无区域性断裂通过，主要为次生的小断层，下游有F6断层通过。该断层带为方解石、铁质、泥质胶结角砾岩；四个平硐揭露处均发育溶洞，充填黏土。溢流坝段区裂隙较为发育，以陡倾角为主，充填物主要为泥质、方解石。河床有J1层间岩性夹层，发育的3条夹层(编号jw1、jw2、jw3)属岩屑夹泥型，在坝体应力影响范围内河床最深夹层为jw3，且夹层不连续。

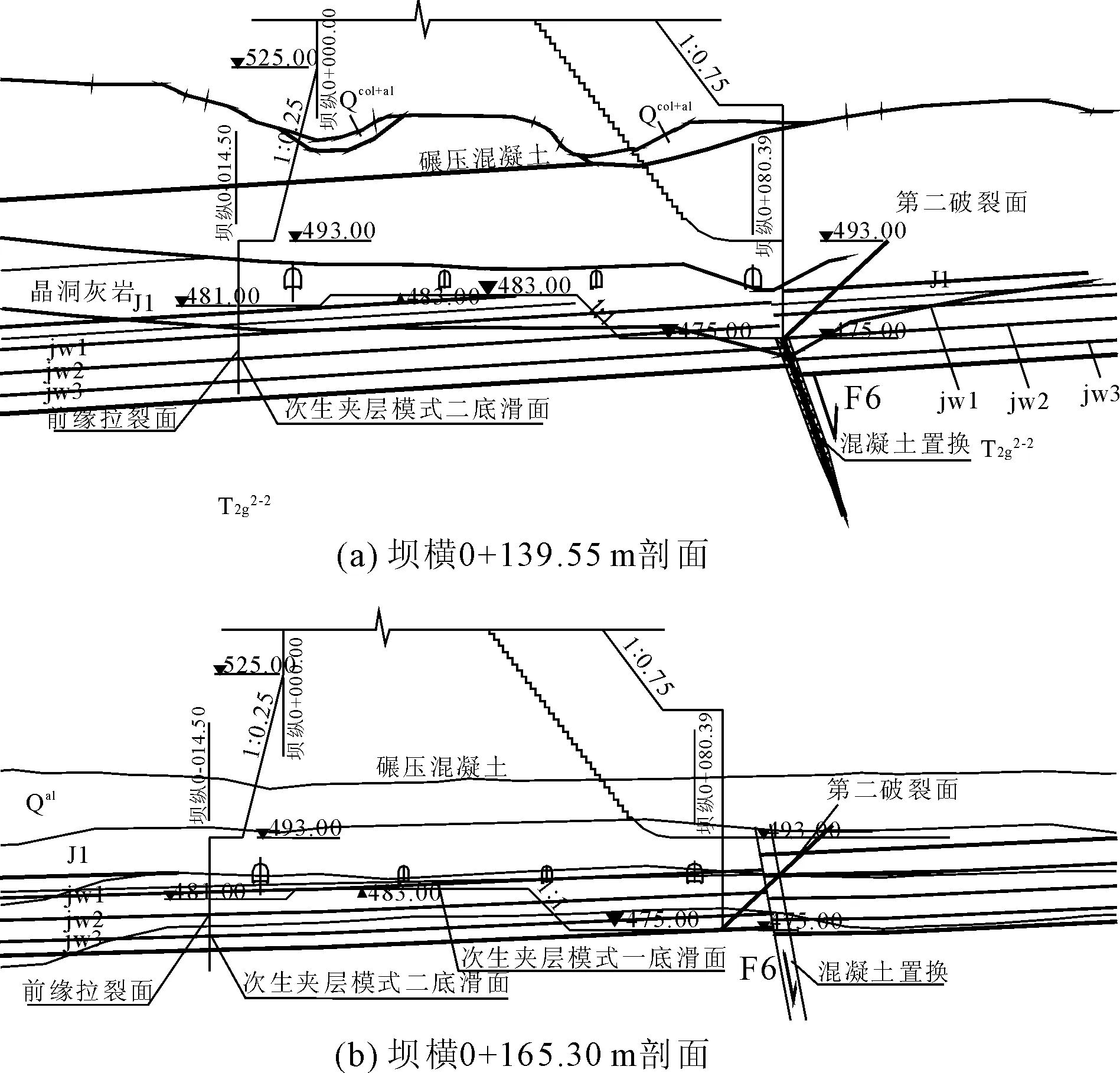
图1 溢流坝段基岩裂隙及断层分布图

根据地质条件，在大坝不设下游侧齿墙情况下，以大坝下游坝趾为次生夹层滑移破坏出漏点，假定上游沿坝踵处拉开，不计拉裂面上的抗滑力，底滑面为层间夹层或岩层层面，连同岩体构成滑动体，尾部岩体沿构造裂隙面或岩体最小破裂角滑出。经过逐层搜索分析，在不做任何工程处理的情况下，只有次生夹层的埋深达到12 m时，充分利用尾部岩体的抗力作用大坝才能达到规范规定的稳定要求。因此，大坝体型设计时参照类似坝基深层抗滑稳定处理的一些工程实例，上采取防渗板和深齿墙相结合的工程措施，即上游侧在坝踵处设置防渗板，防渗板与大坝做成整体式，同时在坝体底面下游侧设置齿墙，切断可能存在的夹层。对F6断层做深挖槽回填混凝土及灌浆处理，以保证不在断层处出现临空滑动面，使齿墙后缘侧尾岩的抵抗作用得到充分利用。

在增加齿墙后根据可组成深层滑动的组合模式进行最不利综合分析后，确定溢流坝段群的深层滑动组合模式为：溢流坝段连同岩体构成滑动体，滑动体底滑面由jw3软弱夹层构成，上游由第四组裂隙构成后缘拉裂临空面，下游为第二组裂隙构成的下游临空面，一种情况视左右侧为临空面，另一种情况考虑与左岸非溢流坝段1/3接触面的作用。

2.3 数值分析模型

溢流坝段坝高117 m，坝底宽100.39 m，坝段宽28.5 m，根据坝体的实际体型，采取合理的简化方式，对溢流坝段及坝基建立有限元模型，详细模拟了闸墩和联系梁及坝体材料分区。坝基部分主要模拟了T2g2-3-1、T2g2-3-2、晶洞灰岩、T2g2-2等岩体。整体有限元模型共有18 404个单元，有20 939个节点。模型基础深度为约3倍坝高，即300 m；自坝踵前沿向上游延伸300 m，自坝踵后沿向下游延伸300 m，坝轴线方向地基范围取坝段宽度。有限元模型以顺水流向为X轴，向下游为正；以坝轴线方向(横河向)为Z轴，从左岸指向右岸为正；高度方向为Y轴，以向上为正。有限元模型在地基底部采用全约束，在地基四周采用法向约束，在坝体横河向采用法向约束(见图2)。

2.4 材料参数及作用荷载

本文考虑现有河谷形状的基岩在自重作用下产生的应力作为初始地应力，采用线弹性本构模型进行计算。坝体为均质坝，混凝土弹模为33.5 GPa，密度2 432 kg/m3，泊松比为0.17。采用的主要岩体材料参数见表1。底滑面jw3夹层(岩屑夹泥型)抗剪断摩擦系数f=0.45，抗剪断强度c=0.10 MPa；坝体左侧接触面的抗剪断强度c=0.97 MPa。

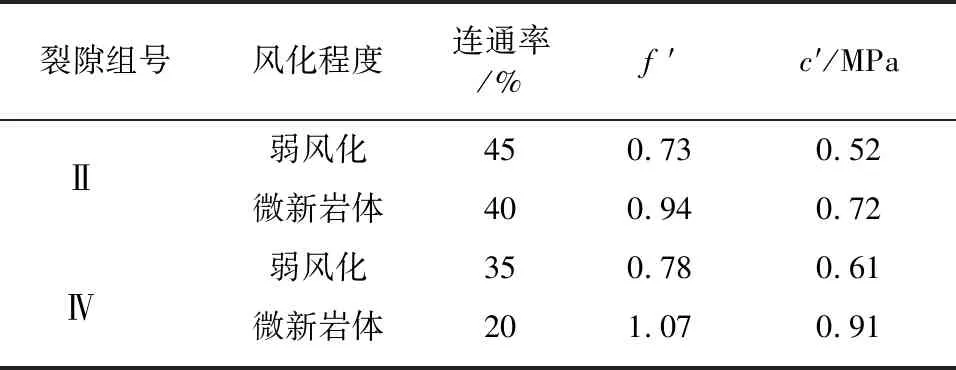
表1 岩体力学参数建议值

计算侧荷载组合为正常工况，基本荷载组合为：上游正常蓄水位水压+下游相应尾水位水压+坝体自重+上游淤砂压力+坝基面扬压力。上游正常蓄水位585.00m，一台机组发电时相应的下游水位507.95m。50年淤积高程523.3 m，泥沙摩擦角Φ=18°，泥沙浮重度γn=8 kN/m3。主要考虑以下5种计算工况：

图2 溢流坝段抗滑计算分析模型

(1) 工况1：采用刚体极限平衡法进行计算，假设溢流坝段下游侧为临空面，不计尾部岩体的抗力作用，不考虑与左岸非溢流坝段坝体接触面黏聚力的影响。

(2) 工况2：采用刚体极限平衡法进行计算，假设溢流坝段下游侧为临空面，不计尾部岩体的抗力作用，考虑与左岸非溢流坝段坝体1/3接触面黏聚力的影响。

(3) 工况3：采用应力代数法进行计算，假设溢流坝段下游侧为临空面，不计尾部岩体对坝体变形的影响，不考虑与左岸非溢流坝段坝体接触面黏聚力的影响。

(4) 工况4：采用应力代数法进行计算，考虑上、下游岩体对坝体变形的约束作用，不考虑与左岸非溢流坝段坝体接触面黏聚力的影响。

(5) 工况5：采用应力代数法进行计算，考虑上、下游岩体的作用，考虑与左岸非溢流坝段坝体1/3接触面黏聚力的影响。

3 计算结果分析

马马崖一级水电站河床溢流坝段底部存在jw3岩屑夹泥型夹层，是影响坝基深层抗滑稳定的主要因素。大坝在水压和自重作用下，根据弹性有限元计算成果，河床中部jw3夹层处于压剪状态，剪应力指向下游，该处的相对滑动趋势较大，在水压力作用下此处可能首先发生压剪破坏(见表2)。

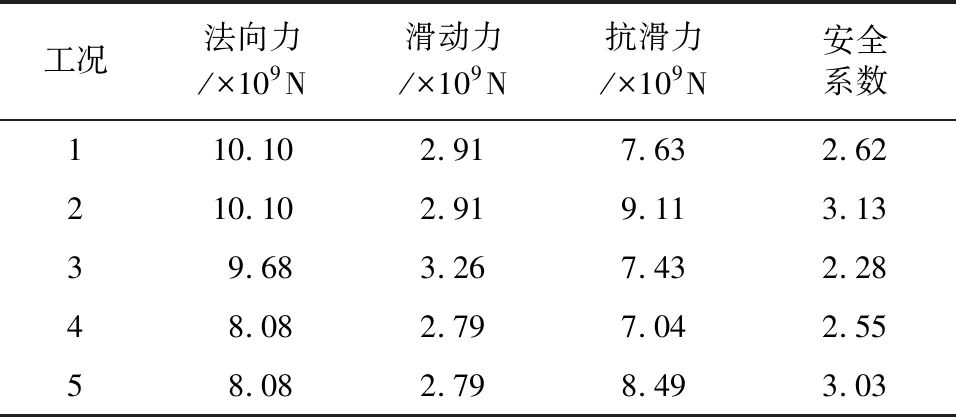
表2 各工况下深层抗滑稳定计算结果

通过三维刚体极限平衡法计算结果可以看出，当假设溢流坝段下游侧为临空面，不计尾部岩体的抗力作用，不考虑与左岸非溢流坝段坝体接触面黏聚力的影响时，在正常荷载工况下，河床溢流坝段群的抗滑稳定安全系数仅为2.62，小于规范规定的3.00。考虑左岸非溢流坝段黏聚力的影响后，抗滑稳定系数增大到3.13，安全系数满足规范要求，但是裕度较小。

根据应力代数和法计算结果可以看出，如果假设溢流坝段下游侧为临空面，不计尾部岩体对坝体变形的影响，不考虑与左岸非溢流坝段坝体接触面黏聚力的影响，计算得到的抗滑稳定安全系数仅为2.28，如果考虑上下游岩体对坝体变形的影响，计算得到的安全系数为2.55，考虑左岸非溢流坝段黏聚力的影响后，抗滑稳定系数增大到3.03，应力代数和法计算结果比采用刚体极限平衡法计算得到的结果偏小。

4 结 论

(1) 马马崖一级水电站河床溢流坝段因底部存在jw3岩屑夹泥型夹层，若不考虑左岸非溢流坝段黏聚力的影响，其抗滑稳定性不满足规范要求，需要对地基进行处理。

(2) 左岸非溢流坝段与河床溢流坝段之间横缝的黏聚力对河床溢流坝段的稳定性具有重要的影响，考虑其黏聚力以后提高了河床溢流坝段的抗滑稳定性，稳定达到了规范要求。因此可以采取左岸非溢流坝段与河床溢流坝段在底部不进行切缝处理，以保证能够提供河床坝段的稳定性。

(3) 如果考虑下游岩体的抗力作用，滑动通道将被阻断，大坝抗滑稳定安全度将大大提高。马马崖一级水电站需要对下游的F6断层进行挖槽回填混凝土和固结灌浆加固处理，提高大坝的整体抗滑稳定性。

(4) 采用应力代数和法计算出的抗滑稳定系数要比刚体极限平衡法得到的抗滑稳定系数小，利用其计算结果进行工程设计要偏于安全。