单双圆柱涡激振动数值模拟研究

林凌霄，陈 威，林永水

(武汉理工大学 理学院，湖北 武汉 430063)

0 引 言

流体经过钝体结构物时会在其两侧产生交替脱落的旋涡，在其表面形成周期性变化的脉动压力，如果结构物是柔性体或者受弹性支撑，会发生涡激振动。在海洋资源开发过程中采用了许多圆柱形结构物，如石油立管、海洋缆索、桩腿等，在海流的作用下，这些海洋结构物都会发生涡激振动。涡激振动在一定条件下会导致结构物的破坏，因此，对涡激振动特点和规律的研究在工程实际中具有很大的应用价值。

在过去的几十年里，许多研究者对圆柱的涡激振动进行了研究[1]。Feng[2]的风洞实验得到了圆柱振幅随约化速度的变化规律，将圆柱的振动响应分成初始分支（initial branch）和下端分支（upper branch）。Khalak 和Williamson[3]研究了小质量-阻尼比组合参数（质量比为m*=2.4，质量阻尼比为m*ξ=0.0013）的圆柱涡激振动，将其振动响应与Feng[1]的结果进行对比，发现圆柱的振动响应发生明显改变，最大无量纲振幅和锁定区域大幅度增大，并在实验中观察到了不同于初始分支和下端分支的第3 种分支，即上端分支（upper branch）。Williamson 和Jauvtis[4-5]对质量比从小到大的单圆柱涡激振动进行了实验研究，发现在较小质量比的情况下，采用两向自由度模型能得到比横向单向自由度模型幅值更大的振动响应。对单圆柱涡激振动的研究，已经取得了一定的研究成果[6-8]。

为了更好地理解圆柱群结构的涡激振动，许多研究者从双圆柱问题入手研究了其绕流特性和涡激振动机理。Zaravkovich[9]对固定双圆柱的绕流问题做了综述，给出了在不同排列方式、间距比和约化速度下圆柱体的受力特征和尾流形态，双圆柱绕流研究可以作为双圆柱涡激振动研究的基础。Zdravkovich[10]，Chen[11]对采用不同布置形式的2 个圆柱之间的相互影响做了研究，发现串列布置时圆柱对尾流的影响大于并列和错列布置圆柱对尾流的影响。姚熊亮等[12]对处于均匀流场中的串列及并列双圆柱涡激振动进行了实验，研究了布置形式对圆柱涡激振动的影响。陈文曲等[13]用数值方法模拟了双圆柱的诱发振动，研究其动力学响应特征。近期国内的研究者如徐晓黎等[14]、秦伟等[15]、盛磊祥等[16]也对并列圆柱涡激振动做了一定的研究分析。

目前对于圆柱涡激振动的研究已经取得了不少成果，然而仍有诸如单圆柱涡激振动在锁定区的特性、并列双圆柱尾流和振动响应随间距的变化等问题值得进一步探索。本文基于CFD 方法对二维单圆柱和并列双圆柱涡激振动展开数值模拟研究，讨论了涡激振动特性以及间距比对双圆柱涡激振动的影响，发现了一些新的现象，如在间距比T*＞4 时的上下侧圆柱振动的不同步现象。

1 计算模型及参数

本文计算模型中，圆柱受弹性支撑，采用了与黄智勇等[18]一致的结构参数（质量比m*=7，阻尼比ξ=0）。由于质量比m*较大的圆柱在顺流向的位移远小于横向[18]，顺流向位移可忽略不计，圆柱仅在横向发生振动。

流体计算区域分别为20 d×10 d 和40 d×20 d，圆柱直径d=0.01 m，尺寸如图1 所示。流体域的左侧边界为速度入口（velocity-inlet），右侧边界为出流（outflow），流动方向水平向右。双圆柱涡激振动计算模型中两圆柱间的相对距离以无量纲距离T*=T/d 表示。

研究中用于描述涡激振动的无量纲数包括约化速度UR、无量纲振幅Ay*、斯特劳哈尔数St、阻力系数CD和升力系数CL，其定义式如下：

式中：U 为来流速；fn为结构在静水中的固有频率。

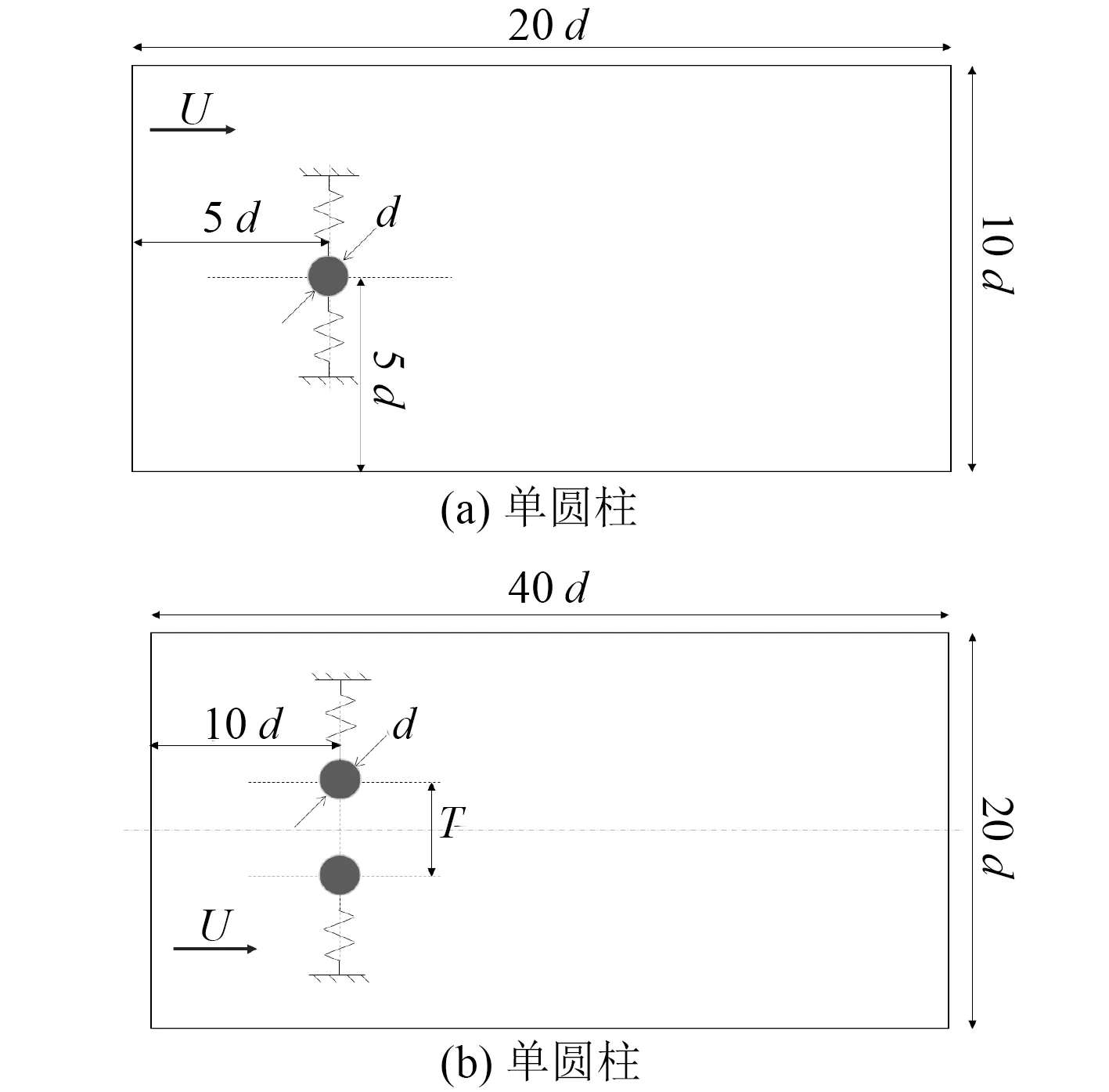
图1 计算模型Fig.1 Calculational model

式中Ay表示结构在横向的振幅。

式中fv为涡的脱落频率。

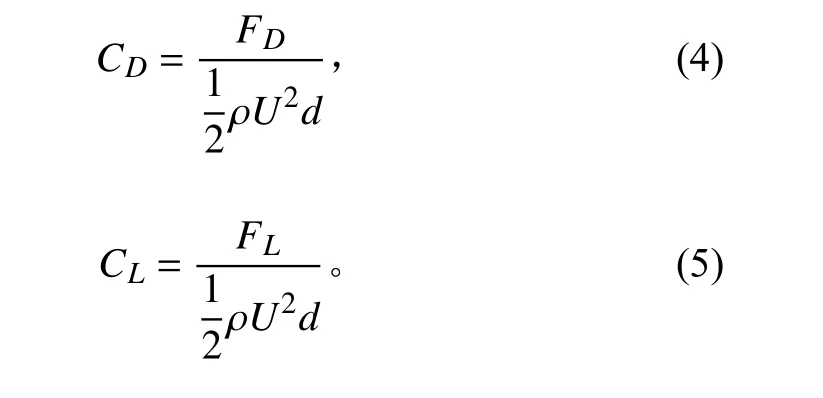
式中：FD为单位长度圆柱在顺流向受到的合力，升力FL为在横向受到的合力。本文用表示阻力和升力系数对时间的平均值，CD,AM，CL,AM表示阻力和升力系数的振幅。

2 单圆柱绕流及涡激振动

对圆柱在Re=100 时的绕流进行了数值模拟，如表1所示。本文的升力幅值、阻力均值以及斯特劳哈尔数与文献结果[17]比较接近，说明本文采用的数值方法对圆柱绕流模型是可靠有效的。

表1 Re=100 的圆柱绕流数值模拟结果Tab.1 Numerical simulation results of flow around a cylinder at Re=100

对圆柱在Re=100 时的涡激振动进行了数值模拟，圆柱振幅随约化速度的变化如图2 所示。本文和黄志勇等的数值计算结果均没有表现出上端分支（upper branch），这与Jauvtis 和Williamson 的实验结果存在一定的差异。造成这种结果的重要原因是：当振动处于上端分支时，振幅响应较大，轴向相关性大大降低，而数值模拟方法采用二维圆柱模型，计算在平面内进行，假定在轴向上变化具有一致性，影响了上端分支的形成。然而，除上端分支之外，本文得到的振幅与黄志勇等的数值模拟结果以及Jauvtis 和Williamson 的实验结果相比，是比较接近的。说明本文的数值模拟方法对弹性支撑圆柱模型可靠有效。

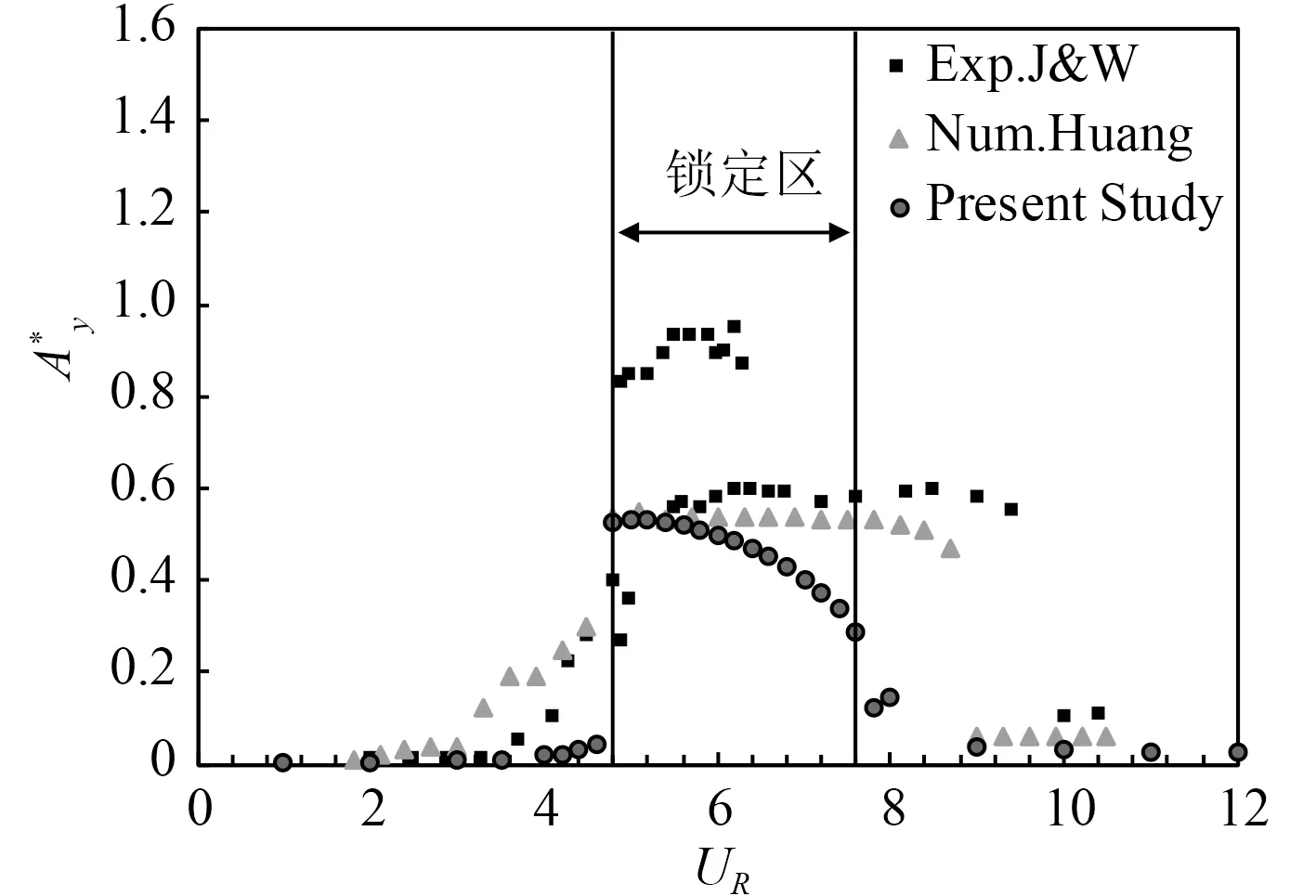
图2 本文振幅响应与已在成果的比较Fig.2 Comparison of the amplitude of present study and previous results

在非锁定区时，圆柱的振幅很小，进入锁定区后，振幅显著增大。在锁定区内，无量纲振幅Ay*保持0.40 以上的较大值，当UR=5 时，圆柱有最大响应振幅0.534。

如图3 所示，当振动处于非锁定区时，频率比与约化速度呈线性关系，满足关系式fv/ fn=St·UR=0.161UR，其中与旋涡脱落相关的St 被认为主要由雷诺数和表面粗糙度决定[19-20]，不随约化速度发生很大改变，是一个相对稳定的值。当振动处于锁定区时，频率比基本不随约化速度发生改变，满足关系式fv/fn=1。这是因为当原有的涡脱频率接近圆柱的固有频率时，涡脱频率会被固有频率锁定。通过分析涡脱频率是否被固有频率锁定，可以判断出涡激振动的锁定区约为4.8＜UR＜7.6。

当UR＜6.6 时，位移与升力系数时程曲线同相，升力对振动起促进作用。尤其是在4.8＜UR≤6.6 的锁定区内，涡脱频率被圆柱固有频率锁定，升力对位移的促进作用显著，造成振幅具有较大增长（见图4）。在6.6＜UR≤7.6 时，位移与升力的相位关系由同相逐渐过渡到反相。当UR＞7.6 时，升力与位移反向，对振动起抑制作用，振动离开锁定区，振幅急剧降低。

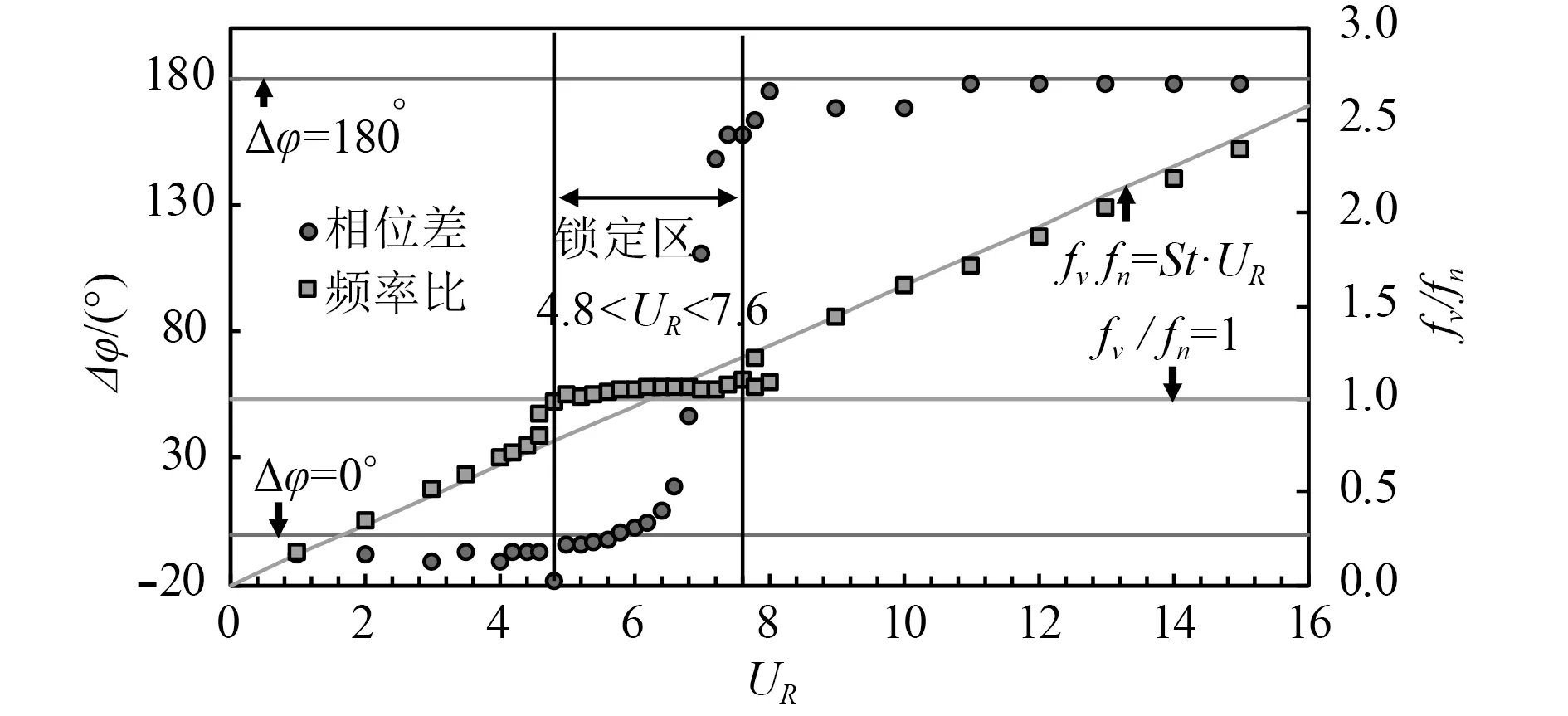
图3 相位差和频率比随约化速度的变化（主y 轴上，Δφ 表示位移与升力的相位差。副y 轴上，fv / fn 表示涡脱频率与圆柱固有频率之比）Fig.3 Phase difference and frequency ratio as functions of the reduced velocity

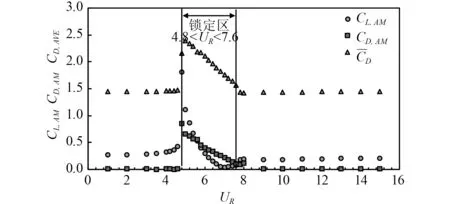
图4 阻力和升力系数随约化速度的变化Fig.4 Drag coefficient and lift coefficient with different reduced velocity

当振动处于非锁定区时，阻力和升力系数较小，与固定圆柱绕流的结果比较接近见（表1）。在锁定区下界，升力、阻力系数发生突变，在UR=4.8 时达到最大阻力系数幅值 CD,AM=0.85，最大升力系数幅值CL,AM=1.8，UR=5.0 时达到最大升力系数均值=2.39，远大于非锁定区的阻力和升力系数，反映出振动处于锁定区时流体和结构的强烈相互作用。在锁定区内，阻力幅值和均值都随约化速度UR上升而逐渐减小。当4.8＜UR＜6.6 时，升力系数随约化速度的增长而减小，由于涡脱频率被圆柱固有频率锁定，振幅仍能保持较大值，但是升力系数对振动的促进作用越来越弱，振幅逐渐减小。当6.6＜UR＜7.6 时，升力系数幅值接近于0，随约化速度增长有小幅回升。

如图5 所示，在锁定区上边界附近UR=7.8 时，升力系数和位移的时程曲线不再是振幅稳定的正弦线，其振幅会随着时间发生变化，这种现象称为“拍振”。对位移曲线做FFT，频谱图上存在2 个靠近的峰值：0.137 Hz 和0.156 Hz（见图6）。经分析，当约化速度UR=4.6，4.8，8.0 时，也出现了拍振现象，表明“拍振”容易在振动处于锁定区下界或上界附近产生。这是因为锁定区边缘处涡脱频率无法完全被圆柱的固有频率锁定，有服从斯托哈尔劳定律的趋势，从而造成响应中可能含有2 种不同频率的成分，一种成分的频率与圆柱的固有频率一致，另一种成分的频率服从斯托哈尔劳定律，而这2 种成分的频率又十分接近，从而产生了“拍振”。

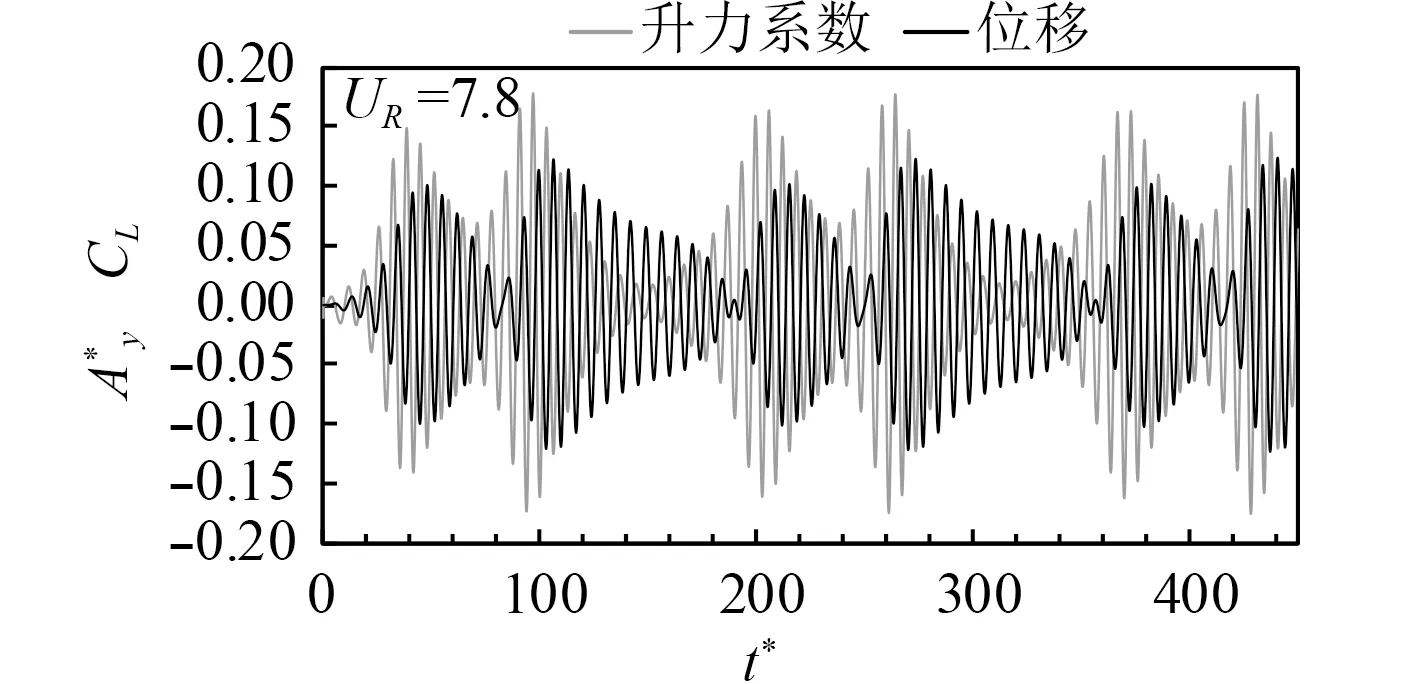
图5 升力系数和位移的时程曲线Fig.5 Time histories of lift coefficient and displacement

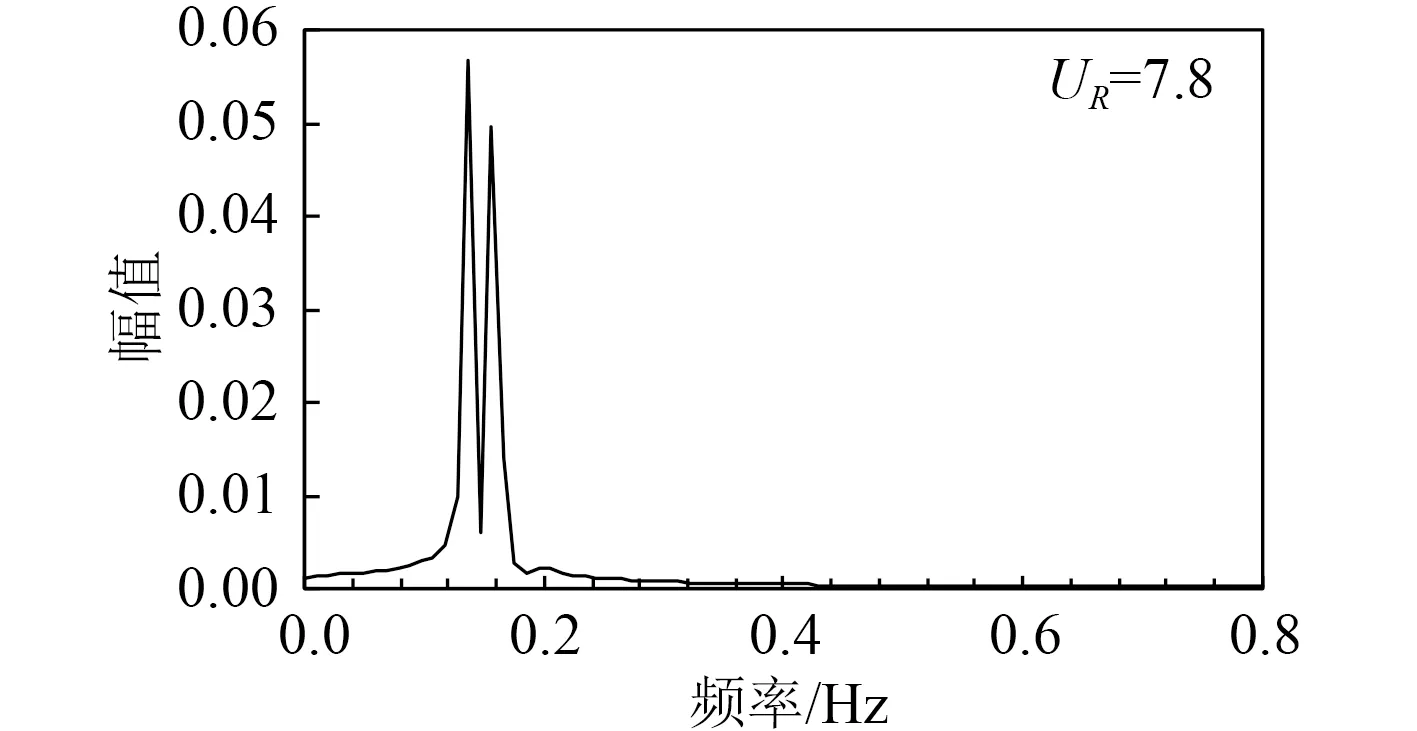
图6 位移时程曲线的频谱分析Fig.6 Frequency analysis of the displacement

3 并列双圆柱涡激振动

基于对单圆柱涡激振动的研究，本文对UR=5.0（对应于锁定区内响应最大值），间距比3.0≤T*≤5.0 的并列双圆柱涡激振动进行了分析。

当3.0≤T*≤5.0 时，间距比越大，流动充分发展、计算结果的幅值达到稳定所需时间越长。这是因为间距比较小时，2 个圆柱下游的涡街存在相互作用越强，2 个圆柱振动积累能量的速度越快，其振幅就越早能够到达稳定。对于间距比T*=5 的双圆柱，双圆柱之间的相互作用较弱，其振幅达到稳定的时间明显增大，与单圆柱涡激振动所需的时间一致。

如图7 所示，3.0≤T*≤5.0 时，升力系数幅值随着间距比的增大逐渐增大，阻力系数幅值逐渐减小，上下侧圆柱升力系数的均值逐渐趋向于0。而两圆柱的振幅值随着间距比的增大相对稳定。间距比增大，2 个圆柱间的相互作用减弱，各个描述流场的无量纲数都逐渐趋向于单圆柱涡激振动的结果（振幅为0.53，升力幅值为1.11，升力均值为0，阻力幅值为0.65，阻力均值为2.40）。

如图8 所示，在间距比T*=4.0 时，双圆柱振动出现了反相同步现象。但在间距比T*=4.5 时，上下侧圆柱的振动具有稳定的相位差，并不再保持反相同步。刘爽[21]对并列双圆柱的研究认为在间距比T*＞3 时，上下侧圆柱的振动处于反相同步状态，本文的结果与其有些不同，结果如表2 所示。在3.0≤T*≤4.0 时，两圆柱的振动反相同步，而在4.0＜T*≤5.0 时，两圆柱的振动不同步。

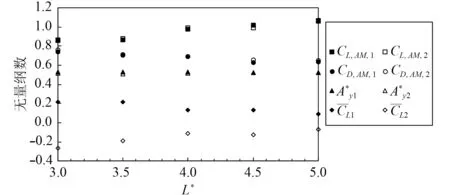
图7 升力、阻力系数和振幅随间距比的变化（图中角标1 和2 分别表示上侧和下侧圆柱的计算结果）Fig.7 Lift coefficient，drag coefficient and amplitude as functions of the space ratio

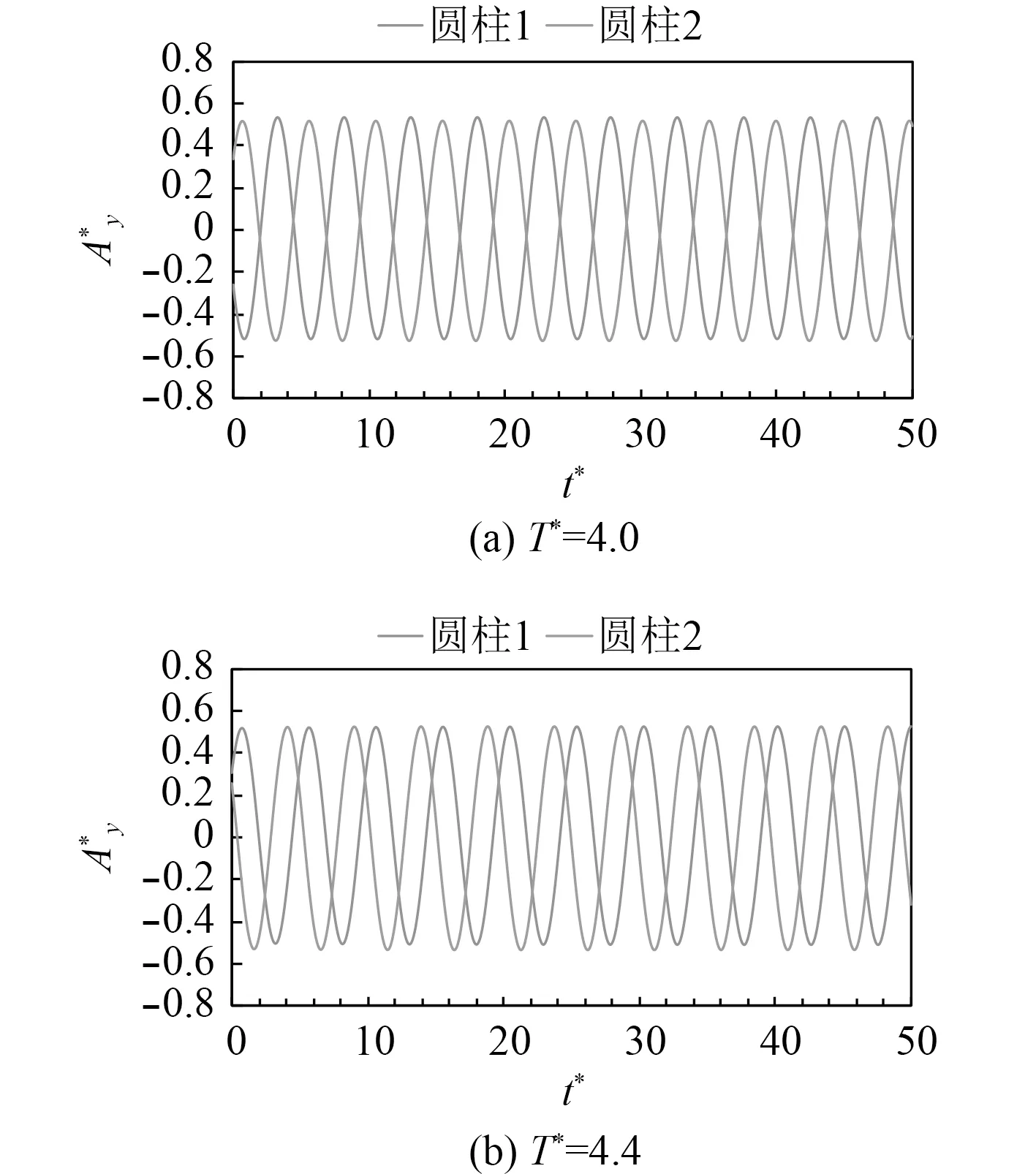
图8 位移的时程曲线Fig.8 Time history curve of displacement

表2 不同间距比下2 个圆柱位移曲线的相位差Tab.2 Phase difference of the displacement for the two cylinders with different space ratio

两圆柱的振动状态同步与否取决于两者之间相互作用的强弱。间距比较小时，两圆柱间的相互作用较强，流场充分发展达到稳定的时间更短，两圆柱的振动状态同步。反之当间距比较大时，两圆柱的振动状态不同步。本文研究得出结论，两圆柱振动状态是否同步的临界间距比是T*≈4。

图8 涡量图Fig.8 Instantaneous isocontours of vorticity

当间距比T*＜4 时，2 个圆柱下游的涡街会互相干扰，内侧方向相反的2 个涡互相融合而消失，导致内侧的涡明显弱于外侧，如图8（a）所示。2 个圆柱之间的相互作用较强。而当间距比T*＞4 时，2 个圆柱下游的涡街不发生干扰，可以清晰地观察到两条独立的涡街如图8（b）。上下侧圆柱的相互作用较弱。

4 结 语

本文基于CFD 方法，对结构阻尼比ξ=0，质量比m*=7 的单圆柱及并列双圆柱涡激振动进行研究，主要结论如下：

1）单圆柱涡激振动的锁定区为4.8＜UR＜7.6，在锁定区内涡脱频率被结构的固有频率锁定，振动响应有较大的增长。当UR=5.0 时，振幅达到最大响应Ay*=0.534。在锁定区边缘，涡脱频率无法完全被圆柱固有频率锁定，容易出现“拍振”。

2）对间距比在3.0≤T*≤5.0 的并列双圆柱涡激振动进行了分析，发现流场充分发展达到稳定的时间随间距比的增大而增加。升力系数幅值随着间距比的增大逐渐增大，阻力系数幅值逐渐减小，上下侧圆柱升力系数的均值逐渐趋向于0，而两圆柱的振幅值随着间距比的增大相对稳定。同时当3.0≤T*≤4.0 时，两圆柱的振动反相同步；当4.0＜T*≤5.0 时，两圆柱的振动不同步，T*≈4 为两圆柱振动是否同步的临界间距比。