图解法和矩值法海洋沉积物粒度参数的对比
2020-10-27李高聪李志强朱士兵张会领曾春华
李高聪,李志强,朱士兵,张会领,曾春华
图解法和矩值法海洋沉积物粒度参数的对比
李高聪1,李志强1,朱士兵1,张会领2,曾春华2
(广东海洋大学:1. 电子与信息工程学院//2. 海洋工程学院,广东 湛江 524088)
【】系统探讨图解法和矩值法计算海洋沉积物粒度参数结果的相互转换关系。首先对雷州半岛南三岛海滩沉积物开展图解法和矩值法粒度参数的对比研究,然后将结果与其他分析结果相结合,讨论两种方法在不同沉积环境中的转换规律。对于南三岛海滩样品而言,两类方法获得的平均粒径和分选系数相关性较高(2≥ 0.821),可相互转换,但偏态和峰态的相关性较弱(2≤ 0.229),不存在相互换算的数学基础;对于不同沉积环境的样品而言,两类方法的计算结果不存在随计算公式阶次增加而相关性逐渐变差的普适规律;两类方法所得的平均粒径和分选系数可相互换算,但偏态和峰态在不同沉积环境中的可换算性差异较大。图解法和矩值法计算的粒度参数在不同沉积环境存在较大差异,不能直接相互替代。
粒度参数;图解法;矩值法;相互换算关系;不同沉积环境
对沉积物进行粒度分析是获取沉积环境的物质来源、物质输运趋势、污染物浓度和沉积环境类别分析等有关信息的重要步骤[1-7]。沉积物粒度分布特征通常使用粒度参数来定量表征。常见粒度参数一般包括4种,即平均粒径、分选系数、偏态和峰态。这些参数分别代表了沉积物颗粒的粗细、均匀性、对称性和相对集中程度,主要受物源颗粒的原始大小和搬运介质的平均动能影响[1-2, 8-9]。计算粒度参数的方法有很多,目前被广泛使用的可分为图解法和矩值法两大类。图解法是基于粒度分析结果绘制出频率累积曲线图,随后在曲线上选择几个具有代表性的点,利用简单计算公式求得粒径参数结果[1-2]。矩值法则将平均粒径值、分选系数值、偏态值和峰态值分别定义为粒度分布的一、二、三和四阶矩函数[8-9]。
在众多的图解法公式中,Folk & Ward图解法计算的粒度参数具有明确的物理意义,应用最为广泛[10-11]。为寻求Folk &Ward图解法和不同矩值法计算得到的粒度参数之间的联系和可比对性,急需开展对不同沉积物环境的沉积物样品关于两类方法计算结果的对比研究。目前,已有众多研究者开展了大陆坡[12]、深海盆地[12]、河口海岸[13]、潟湖[14]、海湾[15]、河口近海[16]和潮滩环境[17]的沉积物样品关于图解法和矩值法计算结果的对比分析,尚还少见对海滩沉积环境的研究报道。为此,本研究利用雷州半岛东北部南三岛海滩的109个沉积物样品开展海滩沉积环境的案例分析。在此基础上,将结果与上述不同沉积环境的研究案例汇总起来,综合探讨图解法和矩值法计算得到的粒度参数之间的关系。本研究有助于提高对不同沉积环境粒度参数关于不同计算方法之间的异同及其原因的认知水平,进而可为未来特定沉积环境粒度参数计算方法的选择提供决策参考。
1 材料与方法
粒度分析样品来自雷州半岛东北部南三岛采样区域受人类活动影响较小的海滩岸段,总长度1.1 km(图1)。采样时间为2018年8月14日低潮位时段,沉积物样品包含了潮上带、潮间带和潮下带共109个表层沉积物样品。采样间隔在沿岸方向上,每隔100 m采集1个样品;在离岸方向上,每隔10 m采集1个样品。实验室样品预处理及分析流程按照《海洋底质调查技术规程》[13]。首先,取适量样品加入烧杯中,并使用质量浓度为10%的盐酸去除样品中的碳酸钙物质;其次,加入双氧水静置12 h以上,去除样品中有机质;随后,加入蒸馏水,稀释过量的盐酸和双氧水,静置24 h以上,并抽掉上部澄清液体;然后,加入0.5 mol/L的六偏磷酸钠溶液,并用超声波振荡10 min来分散样品;最后,将处理好的样品倒入BT-2002激光粒度仪测量粒度。BT-2002激光粒度仪的测量范围为1~2 600 μm,重复性误差小于3%。
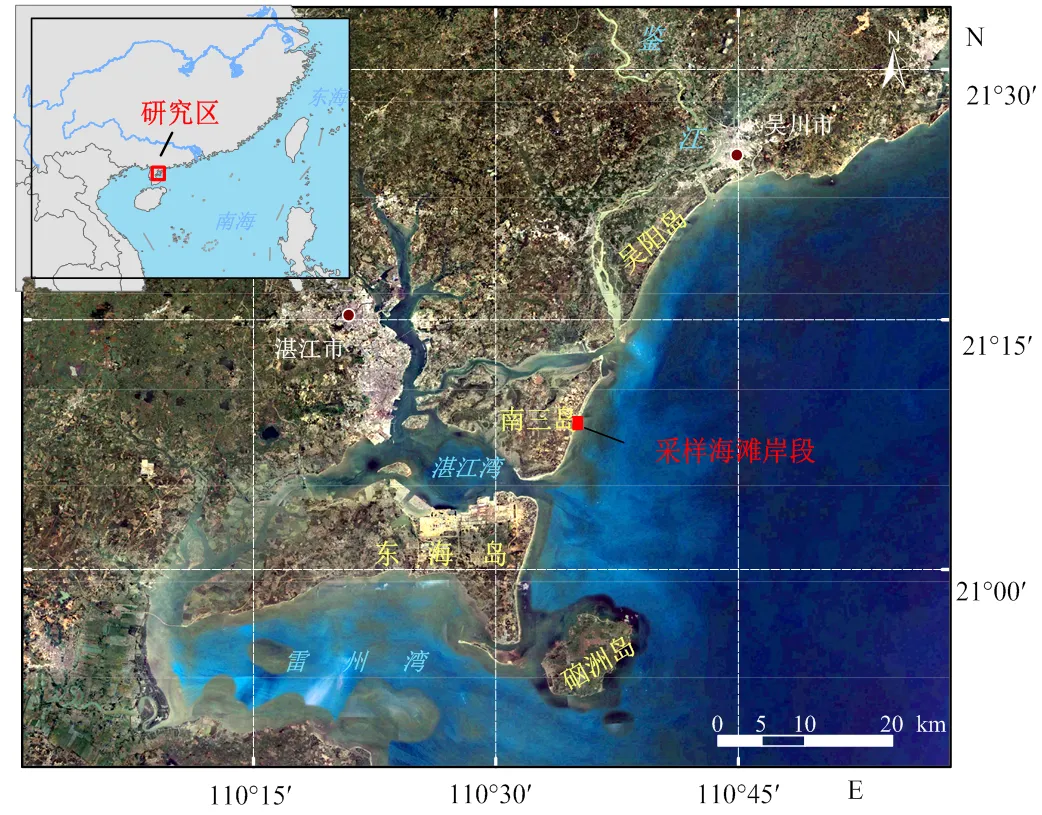
图1 研究区位置
本研究探讨的沉积物粒度参数包括平均粒径、分选系数、偏态和峰态等4类。首先,基于MATLAB的线性内插功能,获取5、1625507584、95和粒级组的中值(X)。其次,利用表1中3种公式,即Folk & Ward的图解法[1]、Friedman的矩值法[3]和McManus的矩值法[4],进行粒度参数计算。随后,通过线性回归分析和作图法评估3种计算方法所得粒度参数结果的相关性。在计算时,由于两种矩值法的平均粒径和分选系数计算公式一致,只对图解法和矩值法的结果进行一次回归分析处理。

表1 沉积物粒度参数计算公式汇总
注:5、162550758495分别对应概率累积曲线上5%、16%、25%、50%、75%、84%和95%的粒径();X为粒级组的中值(),f为各粒级范围的百分比含量。
2 结果
2.1 沉积物平均粒径
结果表明,图解法和矩值法计算的平均粒径数值几乎全部都落在了直线=上(图2a)。线性回归分析表明,图解法和矩值法线性回归的拟合优度达到了0.98(表2),表明两类方法计算的平均粒径数值非常接近,能够相互代替。

表2 图解法与矩值法粒度参数的相关关系统计
2.2 分选系数
相较于平均粒径分布情况,图解法和矩值法计算的分选系数要相对离散一些,但也基本围绕直线分布(图2b)。矩值法计算得到的分选系数略大于图解法计算的结果。两类方法计算结果的拟合优度也较高,达到0.82(表3)。因此,两类方法计算的分选系数可以通过线性关系相互换算。
2.3 偏态
从图2c和2d可以看出,图解法和矩值法计算的偏态值在分布上明显偏离直线。总体而言,图解法计算的结果大于MMFr矩值法计算的结果,但其值比MMMc矩值法计算的结果明显要小。两类方法计算的结果之间缺少线性相关趋势,线性拟合优度数值很小,数值仅为0.23和0.07(表3)。因此,图解法和矩值法计算的偏态不能通过线性关系相互换算。
2.4 峰态
与偏态类似,图解法和矩值法计算的峰态值在分布上显著偏离直线=(图2e、2f)。在数值大小上,图解法计算结果明显小于MMFr矩值法计算结果,但其数值要大于MMMc矩值法计算值。同样,两类方法计算值之间缺少线性相关趋势,线性拟合优度数值仅为0.03和0.16(表3)。因此,图解法和矩值法计算的峰态也不能通过线性关系来相互替换。
3 讨论
Folk & Ward图解法[1]和Friedman矩值法[9]或McManus矩值法[9]是计算沉积物粒度参数最常用的方法[8-21]。两类方法共同之处在于存在一个相同假设,即沉积物粒度分布服从对数的正态分布。不同之处在于图解法仅考虑了90%主要粒级分布情况,而矩值法则考虑了全部粒级分布情况[1-2, 8-9]。可以推论,两类方法计算结果的异同是受检沉积物的粒度分布偏离对数正态分布以及尾部10%粒级分布情况的函数。如果受检沉积物的粒级分布严格符合对数正态分布,这两类方法的计算结果应该完全一致。如果受检沉积物的粒级分布偏离了对数正态分布,则会产生偏差,且偏差程度会随着计算公式阶次的增加而发生显著变化。
为探讨两类方法计算粒度参数结果的偏差情况,需对尽可能多类型的沉积物样品或对不同沉积环境的沉积物样品进行对比分析。基于此,本研究汇总了众多研究者在不同海洋沉积环境中采集的沉积物样品关于矩值法和图解法粒度参数之间的对比分析结果(表3)。结果表明,在大陆坡、深海盆地、河口海岸、堡岛-潟湖、海湾、河口近海和潮滩沉积环境中,图解法和矩值法计算的平均粒径具有非常好的线性相关关系,它们的线性回归拟合优度都大于等于0.940。分选系数情况与此类似,也显示出较高线性相关关系,线性回归拟合优度大多数都大于等于0.940。上述平均粒径和分选系数的情况与本研究基于南三岛地区海滩表层沉积物样品的结果是一致的,表明这一结论具有一定普适性。
但对于偏态和峰态而言,不同沉积环境下图解法和矩值法结果的相关性存在较大差异。在大陆坡、深海盆地和潮滩环境,两类方法计算的偏态和峰态存在较好线性回归关系,它们拟合优度的范围达到了0.669 ~ 0.937。然而,在河口海岸、海湾和本研究的海滩沉积环境中,两类方法计算的偏态和峰态线性关系较弱,拟合优度值仅为0.035 ~ 0.229。从计算公式差异可知,当物质组成均匀和频率分布接近正态分布时,两类方法的粒度参数的相关性会比较高[10-18]。但当沉积物较粗或较细时,由于粒度分布偏离正态分布,且具有明显的尾部特征,两类方法的计算结果差异会随之增大[10-21]。因此,无论在什么沉积环境中,图解法和矩值法计算的平均粒径和分选系数都会存在明确的线性可转换关系,但是对于偏态和峰态而言,线性转换关系仅存在于少数几个沉积环境。
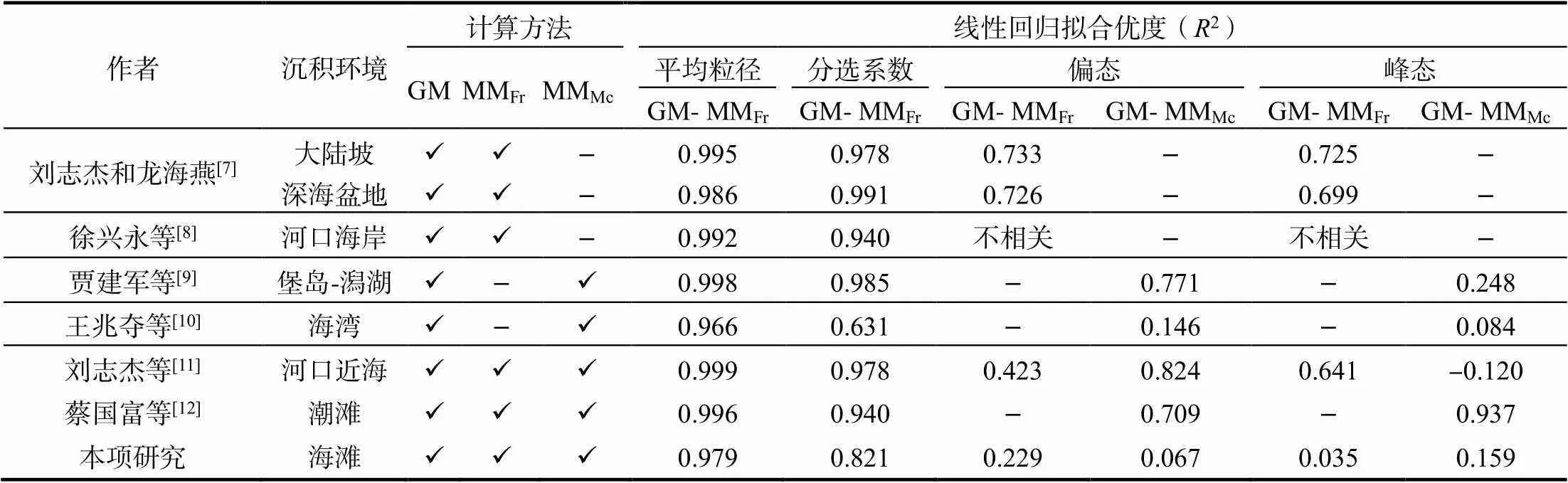
表3 粒度参数不同计算方法的相关性分析结果汇总
为使粒度参数结果便于对比,Folk & Ward[1]根据统计学原理提出基于图解法粒度参数数值结果对应的定性描述术语(表4)。在理论上,当4个粒径参数相关性都较高的情况下,图解法和矩值法结果可以相互转换。基于此,有不少学者利用图解法和矩值法粒度参数的线性转换关系,推导出矩值法粒度参数数值对应的定性描述术语参照表(如表5和表6)[14, 17, 20]。通过对比表5和表6可知,对于偏态和峰态两个参数的描述术语而言,相同术语对应的数值范围是不一致的。其原因在于表5是建立在潮滩沉积环境,而表6是建立在堡岛-潟湖沉积环境,两个环境在物源供给和水动力条件方面存在明显差异。因此,表5和表6 推算出的矩值法定性描述术语仅适用于各自所在研究区(类似于建立了地方参照标准),而不具有普适性。而对于粒径参数相关性较差的研究区而言,图解法和矩值法数值结果不存在相互换算的数学基础,也就不存在传递特定物理指示意义的可能。

表4 Folk & Ward[1]提出图解法粒度参数的定性描述术语

表5 蔡国富等[12]提出的矩值法粒度参数的定性描述术语

表6 贾建军等[9]提出的矩值法粒度参数的定性描述术语
上述分析表明,并不存在普适于各类沉积环境的矩值法粒度参数定性描述术语标准。因此,在今后粒度参数定性分析过程中,建议使用Folk & Ward图解法。如选择了矩值法,则首先要建立其与Folk & Ward图解法4个粒度参数计算结果的线性转换关系。如果线性相关关系明显,则可以仿照贾建军等[9]和蔡国富等[12]的例子,推算出一个适合于研究区的矩值法定性描述术语参照标准。假若不存在明显线性关系,则建议使用Folk & Ward图解法进行粒度参数的计算及其定性分析工作。如在本研究海滩沉积物粒度参数分析中,由于图解法和矩值法计算得到的偏态或峰态并不存在明显线性回归关系,拟合优度仅为0.035 ~ 0.229,故而建议使用Folk & Ward图解法进行粒度参数计算及其定性分析。
4 结论
本研究利用雷州半岛南三岛海滩109个表层沉积物粒度数据,对其开展图解法和矩值法的粒度参数对比研究。在此基础上,通过数据收集方式统计8种沉积环境的两类方法计算得到的粒度参数的线性关系,进而系统分析了图解法和矩值法计算得到的粒度参数之间的关系。本研究得到如下主要认识:
(1)对于南三岛海滩沉积物而言,图解法和矩值法计算得到的平均粒径和分选系数相关性都比较高(2≥0.821),可以相互转换,但两者的偏态和峰态的相关性都比较差(2≤ 0.229),不能相互换算。
(2)对于不同沉积环境的沉积物样品而言,图解法和矩值法计算得到的平均粒径和分选系数的相关性都比较高(2≥ 0.631)。两类方法计算的偏态和峰态的分选系数在不同沉积环境中有不同体现,在大陆坡、深海盆地和潮滩中拟合优度相对较高(2≥ 0.699),但在河口海岸、海湾和海滩环境,两者相关性较差。因此,建议在粒度参数定性分析时,首选Folk & Ward图解法;如选用矩值法,则需建立其与Folk & Ward图解法的线性转换关系。
[1] FOLK R L, WARD W C. Brazos River bar [Texas]; a study in the significance of grain size parameters[J]. Journal of Sedimentary Research, 1957, 27(1): 3-26.
[2] GAO S, COLLINS M. Net sediment transport patterns inferred from grain-size trends, based upon definition of “transport vectors”[J]. Sedimentary Geology, 1994, 81(1/2):47-60.
[3] 张才学, 孙省利, 陈春亮. 湛江港湾表层沉积物重金属的分布特征及潜在生态危害评价[J]. 广东海洋大学学报, 2006, 26(3): 45-49.
[4] 张才学, 孙省利, 陈春亮. 湛江港附近海域潮间带海水、沉积物和贝类体内的重金属[J]. 广东海洋大学学报, 2011, 31(1): 67-72.
[5] 李自超, 蒲晓强, 赵辉, 等. 湖光岩玛珥湖表层沉积物粒度特征及其物源指示意义[J]. 广东海洋大学学报, 2017, 37(3): 93-99.
[6] 黄鑫, 蒲晓强. 热液活动对海底沉积物中有机质的影响[J]. 广东海洋大学学报, 2017, 37(1): 117-124.
[7] 冯钰婷, 彭诗云, 谢辉, 等. 近8000年来珠江口沉积物磁化率及其气候环境意义[J]. 广东海洋大学学报, 2018, 38(3): 49-53.
[8] FRIEDMAN G M. Comparison of moment measures for sieving and thin-section data in sedimentary petrological studies[J]. Journal of Sedimentary Research, 1962, 32(1): 15-25.
[9] MCMANUS J. Grain size determination and interpretation[M]//TRUCKER M. Techniques in sedimentology. Oxford: Backwell, 1988: 63-85.
[10] 赵珍清. 南黄海沉积物粒度分布参数计算方法的比较[J]. 海洋地质与第四纪地质, 1992, 12(3): 95-107.
[11] 付莉莉, 冯秀丽, 杨旭辉. 沉积物粒度参数和频率曲线对粒级划分的响应[J]. 中国海洋大学学报(自然科学版), 2011, 41(9): 83-89 .
[12] 刘志杰, 龙海燕. 南海沉积物图解法和矩值法粒度参数计算及对比[J]. 中国海洋大学学报(自然科学版), 2009, 39(2): 313-316, 336.
[13] 徐兴永, 易亮, 于洪军, 等. 图解法和矩值法估计海岸带沉积物粒度参数的差异[J]. 海洋学报, 2010, 32(2): 80-86.
[14] 贾建军, 高抒, 薛允传. 图解法与矩法沉积物粒度参数的对比[J]. 海洋与湖沼, 2002, 33(6): 577-582.
[15] 王兆夺, 于东生, 罗福生, 等. 图解法和矩法计算泉州湾表层沉积物粒度参数的对比[J]. 海洋地质前沿, 2016, 32(7): 19-27.
[16] 刘志杰, 公衍芬, 周松望, 等. 海洋沉积物粒度参数3种计算方法的对比研究[J]. 海洋学报, 2013, 35(3): 179-188.
[17] 蔡国富, 范代读, 尚帅, 等. 图解法与矩值法计算的潮汐沉积粒度参数之差异及其原因解析[J]. 海洋地质与第四纪地质, 2014, 34(1): 195-204.
[18] 国家海洋局908专项办公室. 海洋底质调查技术规程[M]. 北京: 海洋出版社,2006:63.
[19]INMAN D L. Measures for describing the size distribution of sediments[J]. Journal of Sedimentary Research, 1952, 22(3): 125-145.
[20] BLOTT S J, PYE K. GRADISTAT: a grain size distribution and statistics package for the analysis of unconsolidated sediments[J]. Earth Surface Processes and Landforms, 2001, 26(11): 1237-1248.
[21] ZHOU L, GAO S, YANG Y, et al. Typhoon events recorded in coastal lagoon deposits, southeastern Hainan Island[J]. Acta Oceanologica Sinica, 2017, 36(4): 37-45.
Comparative Study on Grain-size Parameters of Marine Sediment Derived from Graphic and Moment Methods
LI Gao-cong1, LI Zhi-qiang1, ZHU Shi-bing1, ZHANG Hui-ling2, ZENG Chun-hua2
(1.//2.,,524088,)
The interconversion relationship between the grain-size parameters of marine sediment calculated by graphic measures (GM) and moment measures (MM) is investigated in this study.First, a comparative study on grain-size parameters of beach sediment of Nansan Island, Leizhou Peninsula, has been carried out. Then, the comparative results of various sedimentary environments are collected to systematically analyzed the transformation relationship between the results of GM and MM.The results show that: in terms of the beach sediment, the mean grain size and sorting coefficient calculated by GM and MM both have a high correlation (2≥ 0.821), which means that they can be converted to each other; but the correlation of the skewness and kurtosis are very poor (2≤ 0.229), which means they cannot be converted to each other; for sediment samples of different sedimentary environments obtained by statistical methods, no general rule of the relationship of particle size parameters between GM and MM is found with the increase of moment; the mean grain size and sorting coefficient of GM and MM can be converted to each other, but there is a great difference in the convertibility of the skewness and kurtosis calculated by GM and MM in different sedimentary environments.It is suggested that the conversion relationship of the grain-size parameters between moment measures and the folk & Ward graphical method need to be clarified, before using MM to describe the physical meaning of the particle size parameters of sediments.
grain-size parameters; graphic measures; moment measures; mutual conversion; sedimentary environments
P736.21
A
1673-9159(2020)06-0096-06
10.3969/j.issn.1673-9159.2020.06.012
李高聪,李志强,朱士兵,等. 图解法和矩值法海洋沉积物粒度参数的对比[J].广东海洋大学学报,2020,40(6):96-101.
2020-04-13
国家自然科学基金项目(41676079); 广东海洋大学创新强校工程项目(Q18307)
李高聪(1987-),男,博士,讲师,研究方向为海洋地质学,Email: ligaocong2013@163.com
李志强(1974-),男,教授,研究方向为海滩过程和海岸工程环境,Email:qiangzl1974@163.com
(责任编辑:刘岭)
