一种基于统计学模型的城轨信号系统故障诊断方法

谭力天，陈 昕，李澎东

（湖南中车时代通信信号有限公司，湖南 长沙 410005）

0 引言

基于通信的列车运行控制系统（communication based train control, CBTC）主要包括列车自动驾驶（automatic train operation, ATO）、列车自动防护（automatic train protection, ATP）、区域控制器（zone controller, ZC）、联锁（computer interlocking, CI）、列车自动监控（automatic train supervision, ATS）及数据通信系统（data communication system, DCS）等子系统[1-2]。在系统运行过程中，各子系统间数据实时交互，会产生大量的日志数据。由于子系统记录日志数据具有专业性，使得数据分析成为一项繁重、复杂的专业工作。目前对运行数据的分析与CBTC 系统故障定位不仅严重依赖工作人员专业技能，同时只能被动地等待问题出现后以时间点去定位故障位置，处理问题效率低但对工作人员专业技能要求高。

目前，在故障诊断方面，故障诊断专家系统应用人类专家的知识和解决问题的方法，通过建立知识库与推理机，实现确定性故障诊断[3]，其被应用到ZPW2000A型无绝缘移频闭塞设备的故障诊断，通过归纳常见故障类型及特征，实现专家系统功能模块的构建[4]；小波分析和深度信念网络概念被引入到列车牵引系统故障诊断之中，在离线机车记录分析中发挥了作用[5]；模糊Petri网络模型与神经网络算法的结合应用，实现了故障诊断算法的动态自适应，提高了故障诊断的准确度[6]；而统计学方法适用于大数据系统，其基于多向保局投影[7]进行过程监控故障诊断，利用统计学特性将过程监控的故障数据投影到统计模型中，从而获得故障特征[8]。基于统计学的模型故障诊断方法主要包括贡献图法、结构化残差法、信号重构法和模式分类法[9]，其中模式分类法是通过统计方法获得故障的表征模式，由于不同的故障在特性上通常具有相似性，通过建立故障信息库，可以采用模式分类方法对故障进行分类。统计学马尔可夫模型是以简单的表述解决复杂的问题，自20 世纪80 年代开始被陆续成功地应用于语音识别、机器翻译、拼写纠错、图像处理和基因序列分析等多个领域[10-11]。文献[3-4]中故障诊断专家系统需要搭建知识库与推理机进行故障诊断，较统计学方法复杂；文献[5-6]在实时故障诊断方面应用较统计学方法还不成熟；而统计学方法应用成熟可靠，其大数据特性适用范围广，并已经在城市轨道交通领域列车自动监控方面取得应用。为此，本文提出一种基于统计学模型的故障诊断方法，以实现对城轨CBTC 信号系统故障的快速、准确定位。

1 CBTC 系统故障诊断现状及分类

1.1 故障诊断现状

针对CBTC 系统故障，相应系统的运营或售后服务人员凭借自身的经验和知识，通过分析故障时间段内日志数据来进行维护和故障分析。在实际维护过程中，各子系统间的配合和运营或售后人员的技术水平直接影响故障分析的效率和准确性，在很多情况下需要研发人员介入分析。运营或售后人员及研发人员需依靠培训或学习来提高技术水平，易受到人员流动或成长周期等因素影响，成本较高、成效较慢。

CBTC 系统是地铁运营中的“大脑”，需各子系统密切联系、相互协作，使得故障现象表征子系统和实际故障子系统可能不一致，单独分析子系统不能及时定位故障，需要多个子系统专业人员的相互配合，效率低，通用性不强。

在CBTC 系统运行过程中产生的大量日志数据只有在系统故障时才会用来进行分析，系统正常运行过程中大量数据被保存但未被充分利用，造成数据的“浪费”，而采用统计学模型对日常数据进行分析处理，利用数据特性建立对应模型，通用性较强，适用范围较广，不仅可以快速定位系统故障，还可以提供一定的故障预警。

1.2 CBTC 系统故障分类

CBTC 系统是由多个子系统构成的复杂系统，子系统间相互协作，保障列车正常运行。CBTC 系统故障的原因较为复杂和多样，各子系统都具有相应的日志记录作为故障分析的基础。CBTC 系统各子系统关联关系如图1 所示。

图1 CBTC 子系统间关联关系Fig. 1 Subsystem association of the CBTC system

DCS 提供图1 中各子系统设备间安全、可靠的数据交互。列车运行速度控制级别由低到高分别为联锁控制级别（IXLC）、点式列车控制级别（ITC）和连续列车控制级别（CTC），其中CTC 级别下列车运行效率最高，是正常运营过程中最常用的级别。ZC 是在CTC级别下的核心设备，本文以ZC 为例进行故障分类分析。

为快速定位故障原因，对所有涉及ZC 并在ZC 中有异常现象的故障进行分类，并利用统计学进行建模。基于现场，涉及ZC 的关联故障主要有：（1）列车与ZC 通信故障，ZC 表现为将该车置为安全态；（2）CI与ZC 通信故障，ZC 表现为将该CI 涉及轨旁设备置为安全态；（3）相邻ZC 与ZC 通信故障，ZC 表现为将该相邻ZC 涉及并与本ZC 相关联的轨旁设备置为安全态；（4）轨旁设备故障，ZC 表现为将该轨旁设备涉及移动授权计算按安全态处理；（5）列车升级CTC相关设备故障，ZC 表现为该列车始终无法升级为CTC级别；（6）列车运行异常，ZC 表现为将该列车置为安全态；（7）ZC 软件故障，ZC 表现为涉及范围内的列车非正常置为安全态；（8）ZC 硬件故障，ZC 表现为设备状态置为安全态。

2 统计学模型

统计学模型依赖于所采用的样本数据，样本数据越全面、充分，对应的模型越准确。针对地铁运营的特性，随着其运营里程的增长，设备故障数据样本逐渐增多，其可用性和全面性也越佳，则越有利于提高统计学模型的性能。

2.1 马尔可夫模型

假定某一故障出现的概率为一条件概率值P(S)，认为该故障受w1, w2, …, wn共n 个不同事件共同影响，则该故障出现的概率P(w1, w2,…, wn)按照条件概率公式展开后为

其中，P(w1)表示第一个事件发生的概率；P(w2|w1) 表示在已知第一个事件发生的条件下，第二个事件发生的概率；以此类推，P(wn|w1, w2,…, wn-1)表示在已知前n-1 个事件的发生条件下，第n 个事件发生的概率。

实际应用时，到第三个事件，其条件概率P(w3|w1, w2)的计算就已较为复杂并且会花费较多资源。为了解决这种不利局面，马尔可夫提出了相应的简化模型，即针对复杂的条件概率问题，假设任意事件wi(i=1, 2, …, n)的条件概率只同其前一个事件wi-1有关，于是P(S)可以表示为

式（2）为统计学二元模型。考虑到时间和空间的资源消耗与模型精确性间的平衡，本文采用二元模型。

在ZC 关联故障分析中，只考虑当故障前提条件发生时故障概率的统计，即ZC 关联故障分类与实际故障原因之间的概率统计关系。

2.2 模型的训练方法

根据大数定理，以采样数据观察结果作为统计学概率计算基础。由于统计观察结果存在局限性，那么有这样一种可能性，即在观察结果中虽未出现某一故障，但是从概率角度不能认为这种情况不会发生。首先，采用古德-图灵方法对出现次数非常少（少于经验阈值）的条件事件减小条件概率，经过上述处理后的概率称之为相对频度；其次，为了保证所有条件概率之和为1，同时为了避免在统计过程中出现未发生故障的概率为0 的情况，需保证训练用数据样本的全面性和充分性，并为统计没有出现的事件进行条件概率分配，即补偿相对频度。卡茨退避法是一种概率平滑方法，模型训练时采用该方法处理零概率问题，并采用概率拟合的方式对统计学概率进行连续平滑，具体处理表示为

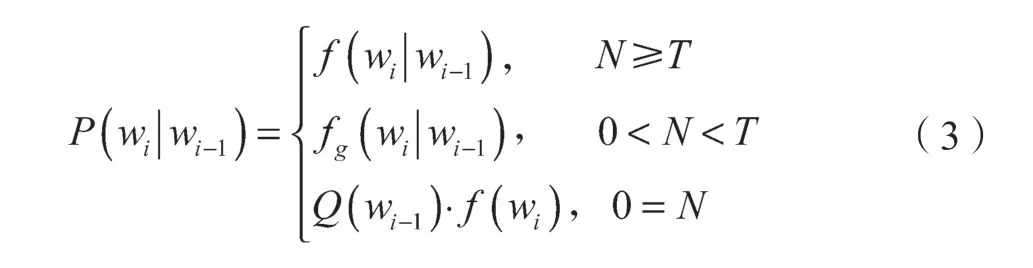
式中：wi-1——故障原因；wi——故障现象；f()——统计学相对频度；fg()——统计学采用古德-图灵估计后的相对频度；Q(wi-1)——估计补偿相对频度；N——统计学频次；T—相应阈值，统计频次不小于阈值，则认为概率估计与相对频度一致。

训练过程如下：

（1）数据预处理。首先明确选用数据的可靠性和有效性，而后以随机抽样的方法选择数据样本。

（2）训练参数调整。为保证训练结果符合上文概率要求，适当选择式（3）中的T 值（经验值一般在8～10 之间，可根据实际情况做调整），保证概率估计曲线平滑。

3 统计学故障诊断模型的应用

本文以ZC 关联故障为例建立故障诊断统计学模型，以故障时刻前后1 h 数据作为故障数据样本，通过确定故障分类，构建故障诊断系统的测试集,测试所有故障分类。对应ZC 关联故障总结：（1）w11为列车-ZC 通信故障，w12为列车安全态；（2）w21为CI-ZC 通信故障，w22为该CI 涉及轨旁设备置为安全态；（3）w31为相邻ZC-ZC 通信故障，w32为该相邻ZC 涉及与本ZC相关联的轨旁设备置为安全态；（4）w41为轨旁设备故障，w42为将该轨旁设备涉及移动授权计算按安全态处理；（5）w51为列车升级CTC 相关设备故障，w52为该列车无法升级为CTC 级别；（6）w61为列车运行异常，w62为将该列车置为安全态；（7）w71为ZC 软件故障，w72为涉及ZC 范围内的列车非正常置为安全态；（8）w81为ZC 硬件故障，w82为设备状态置为安全态。

本文采集数据样本随机选取调试运行阶段ZC 系统一个月内的运行数据，在所有样本中随机选择800 组作为训练数据样本，随机选择其中的75%为训练数据，25%为测试样本验证训练结果，尽可能完整地包括了本文所定义的所有ZC 关联故障类型。用古德-图灵方法对ZC 硬件故障统计概率为0 的事件进行了处理，利用卡茨退避法获得ZC 关联故障的数据统计概率（图2）。图中通过概率平滑处理曲线拟合，纵坐标为相对频次，表示故障统计的概率拟合；横坐标为故障分类。

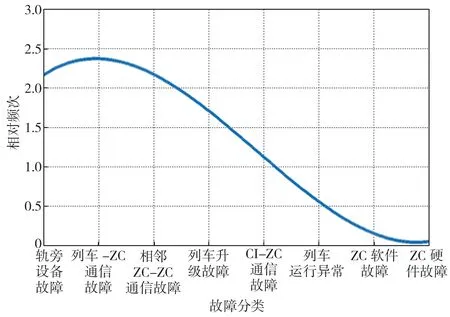
图2 故障概率分布拟合曲线Fig. 2 Fitting curve of fault probability distribution

4 统计学故障诊断方法验证

在长沙轨道交通4 号线调试运行阶段对本文方法进行验证应用，通过对8 类ZC 关联故障进行测试，201 组故障诊断测试结果如表1 所示。通过验证，可以看到其中列车-ZC 通信故障、CI-ZC 通信故障、相邻ZC-ZC 通信故障和ZC 硬件故障的分类诊断准确率均为100%，统计学方法模型对通信类故障、硬件类故障识别率最高；而对列车运行异常和ZC 软件故障的分类诊断准确率较低，其中ZC 软件故障诊断准确率最低只有84.21%，由于ZC 软件故障在故障总体分布中所占比例较低，导致部分该类故障易被误判，本验证应用给调试运行提供了有效数据支撑和判断依据。可见基于统计学的故障诊断模型可以较好地定位故障，有利于提高调试或维护人员的工作效率。

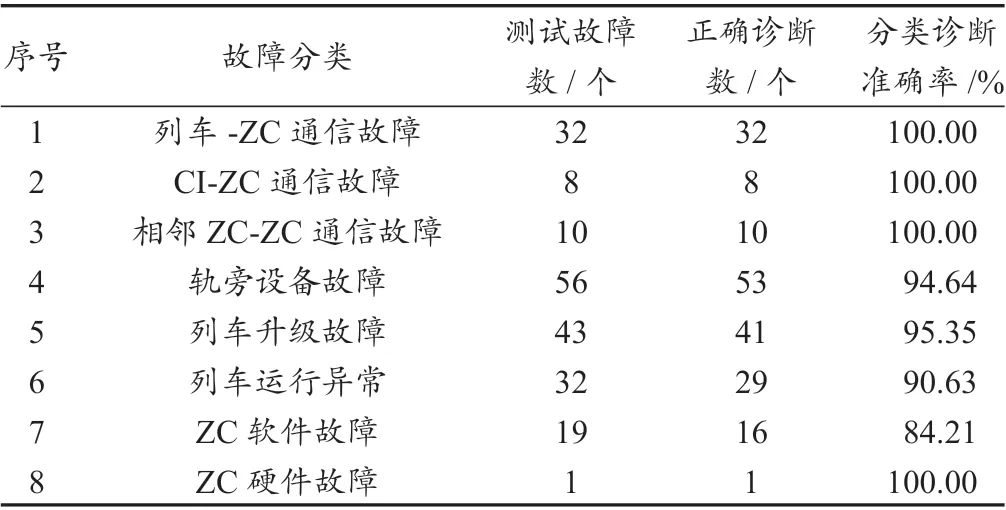
表1 ZC 关联故障分类测试结果Tab. 1 Test results of ZC associated fault classification

5 结语

本文提出了一种基于统计学模型的故障诊断方法，并以ZC 关联故障为例，通过统计学方法提取故障样本数据，建立并训练故障诊断模型。在长沙轨道交通4 号线调试运行阶段的验证应用表明，该故障诊断模型可以用于CBTC 系统故障诊断快速定位。在智慧城市建设中，城市轨道交通的智能化运维是一种趋势。在提高故障诊断的准确性、快速性、实时性和适用范围，实现系统高度集成、大数据分析、调度综合统筹等方面，统计学方法是未来维护智能化的有效手段。同时，对于在统计学中分布概率值在总体分布中占比较低的分类，其故障诊断正确率较低的问题，下一步可以在本文所提方法的基础上应用模式识别法来提高故障诊断正确率。