均匀圆形频控阵非线性频偏的波束仿真分析

柯 凡，张正文

(湖北工业大学电气与电子工程学院，湖北 武汉 430068)

Mahmood等人[2]提出了基于三角函数的形式的分段频偏，该方法有更好的峰值旁瓣比和更窄的主瓣。Y. Ma等人[3]分析了FDA频率增量和波束形成的关系，提出了一种聚焦波束形成的数学优化方法。王博等人[4]采用非线性偏频的思想研究频控阵的波束控制，扩展了频控阵研究方向。Gao等人[5]提出平方增长形式非线性分布的频偏FDA(square-FDA)，分析了距离与角度耦合的原因。平方频偏分布频率分集阵列雷达主瓣波束宽度更窄，发射波束的能量聚焦在一个目标点上，能够减缓目标定位在距离维和角度维的模糊性。王文钦[6]基于阵元非均匀分布，提出非均匀线性间隔排列的频控阵，阵元间间隔不是等距的，阵元间的频偏是线性分布的，间距与波长有关。模型固定后，载频和频偏不能随时间改变，没有应用前景。王文钦基于阵元均匀分布，结合非线性增长的正弦频偏形式的FDA(sin-FDA)，消除了距离和角度维的耦合性，但会有点状旁瓣凸起，使得整个旁瓣级变大[7]。Khan等人[8]将均匀线性阵列和对数增长的频偏相结合，提出log-FDA(logarithmically increasing frequency-offest FDA，log-FDA)雷达，能在期待目标位置形成点状波束，减弱了线性增长频偏频控阵雷达的距离和角度的耦合特性，但在距离维和角度维的波束都较宽，分辨率不高。

针对以上问题，基于均匀圆型阵列模型，提出了基于非线性频偏的频控阵雷达发射波束形成方法。在分析UCFDA阵列结构的基础上，推导了基于线性频偏的频控阵发射信号处理模型；而后构建四种非线性频偏函数，提出了基于非线性频偏的圆型频控阵发射信号处理模型。最后数值仿真了提出的四种非线性频偏的有效性。

1 均匀圆阵频率分集阵列(UCFDA)

均匀圆阵频控阵模型见图1。

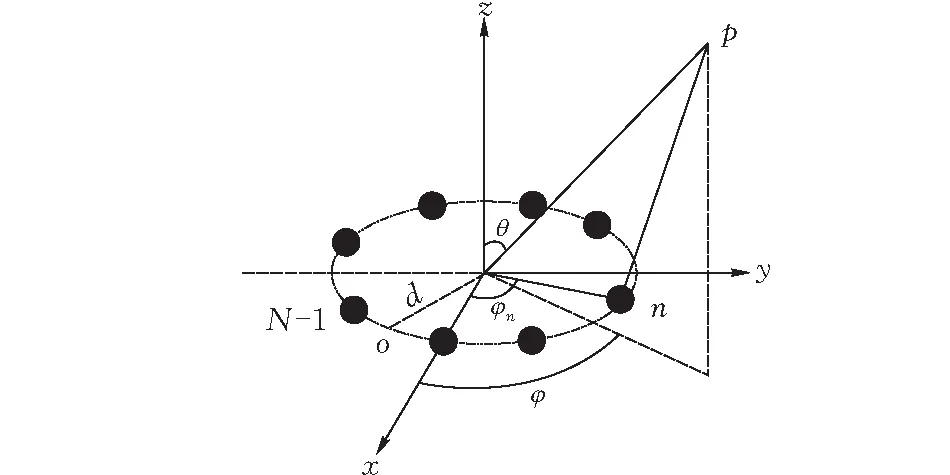
图1 均匀圆阵频控阵模型

rn=r-dsinθcos(φ-φn)

(1)

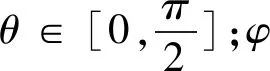
图2为均匀圆阵频控阵模型。其中圆的半径为d，第n个阵元的发射频率

fn=f0+g(n)Δf，n=0,1,…,N-1

(2)

式(2)中，n为阵元序号，N为真元的总个数。g(n)是n的离散函数，f0为雷达的中心频率，Δfn为第n个阵元相对中心频率的频偏，同中心频率不是一个数量级，远小于中心频率。设第n个阵元的发射信号为单频信号：

sn(t)=anexp(j2πfnt)，n=0,1,…,N-1

(3)

式(3)中，an为复权重系数。考虑到传播时间，到达空间中任意点的发射信号可表示为：

检验检测中心要努力探索，找问题、挖隐患，消除监测抽检风险。在制定抽样监测工作方案时，以查找问题为主导，多抽检基层市场的散装食品，在采样时，多采“三小”行业生产的食品，特别注意把群众消费量大的食品品种、高风险品种、新批准原料生产的品种、通过其他渠道已经发现问题的品种等作为抽检监测的重点。同时积极探索新的抽检监测方式，集中力量确定若干重点食品品种，有针对性地加大抽检频次，并定期跟踪。同时，强化监管整改措施，倒逼企业加强自检送检，集中精力解决了一批风险隐患问题，树立一批放心食品品牌[2]。

(4)

将式(1)和式(2)带入式(4)

(5)

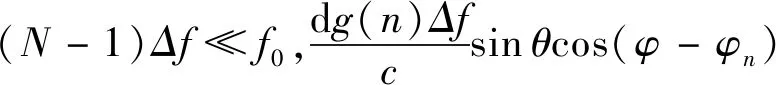
(6)

阵元发射信号到达空间任意点p(r,θ,φ)的阵列因子

(7)

由式(6)知第n个阵元相较第0个阵元的发射信号相位差为：

所以FDA波束到达最大值点的条件为：

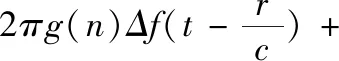
(8)

式(8)得知UCFDA雷达的波束特性与距离R、仰角θ、方位角φ、时间t均有关。

2 基于非线性增长频偏的UCFDA雷达

当阵元间的频偏为线性增长形式时，g(n)=n，即fn=f0+nΔf,n=0,1,…,N-1。基于公式(7)，固定时间t=0，当an=1,n=0,1,…,N-1,即不加权重，仿真参数为：阵元数N=16；载频f0=3 GHz；圆阵半径d=1.2λ；q=30°；φ=120°。

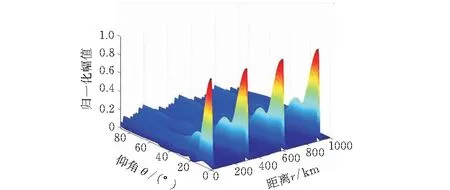
(a)固定方位角φ=120°

距离-仰角维波束图(图2a)中，随着距离的增加仰角维栅瓣越来越大。距离-方位角维波束图(图2b)中 ，形成多个尖峰。消除距离与角度耦合方案有：阵元间距等距离，每个阵元相对中心频率的频率偏移是非线性增长的，这种方法容易实现，广泛被研究；阵元间距与发射频率成反比，每个阵元相对中心频率的频率偏移是线性增长的，由于阵元间距随发射频率变化，实时性不高。针对距离-角度耦合的问题，基于均匀圆阵的模型，分别引入对数、平方、正弦、对数结合三角等非线性频偏，对比不同方案波束图的效果。分别记为g2(n)、g3(n)、g4(n)、g5(n)，即：

(8)

若要将非线性增长下的波束指向空中任意一点p(r0,θ0,φ0)，则第n阵元的权系数

an(r0,θ0,φ0)=

将式(8)代入式(7)，得

3 仿真分析

假定目标位置(500 km,30°,120°)，时间t设定成0 s，归一化UCFDA仿真参数为：阵元数N=16；载频f0=3 GHz；圆阵半径d=1.2λ；r0=500 km；q0=30°；φ0=120°。统一仿真尺度，比较不同方案频偏的UCFDA的波束特性，将距离参考阵元的频偏设置为15 kHz。不同方案每个阵元的发射频偏见图3。不同方案相邻阵元之间的间隔频率见表1。

图3 各种形式下每个阵元的频偏示意图

表1 各种形式下每个阵元的频率增量

图4展示了在以上参数设定下的log-UCFDA、square-UCFDA、sin-UCFDA、log+sin-UCFDA的仰角-距离维波束能量分布图。加入非线性频偏后，各种形式频偏均能在目标位置形成点状波束，有效地消除了线性UCFDA中的仰角距离耦合问题。但仰角维的主瓣宽度都较宽，特别是log-UCFDA在距离维形成跨度较大的“拖尾”波束。相比四种频偏，log+sin-UCFDA仰角维主瓣最窄，但在距离维有“拖尾”波束。

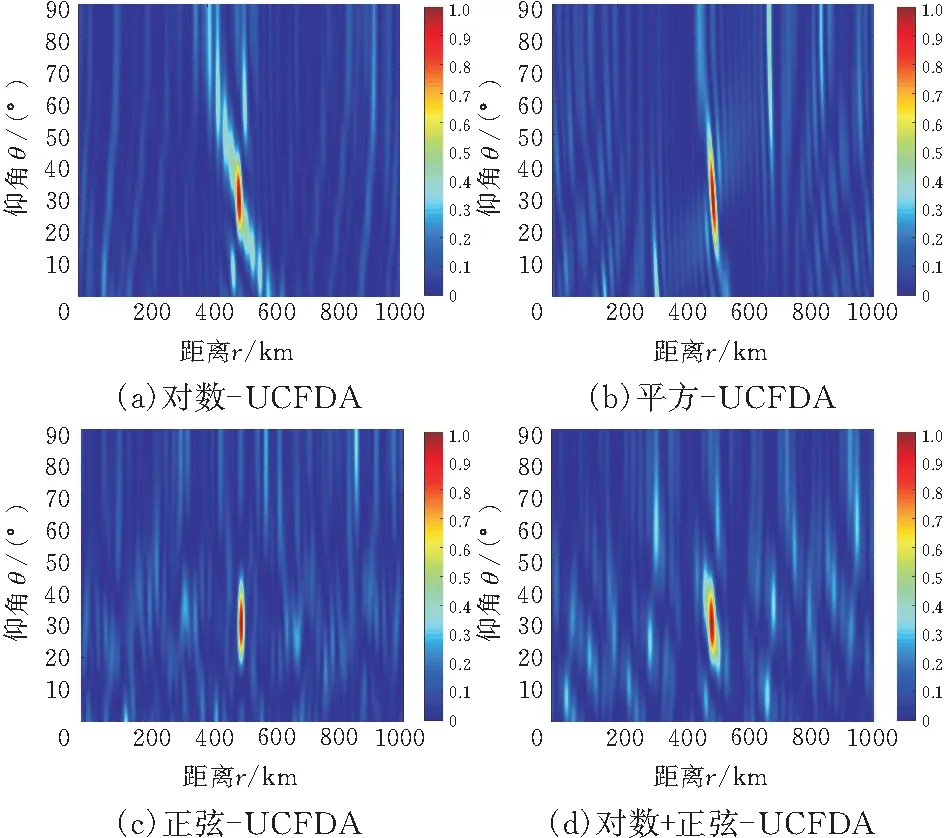
图4 仰角-距离维波束图

图5展示了log-UCFDA、square-UCFDA、sin-UCFDA、log+sin-UCFDA的方位角-距离维波束能量分布图。在方位角维和距离维都能形成较窄的波束，square-UCFDA点状效果最好，但是在距离维形成“拖尾“波束。

图5 方位角-距离维波束图

图6展示了log-UCFDA、square-UCFDA、sin-UCFDA、log+sin-UCFDA仰角-距离维关于仰角的波束特性。在仰角维，sin-UCFDA的主瓣宽度为20.0°。旁瓣级为0.352，也比较低。

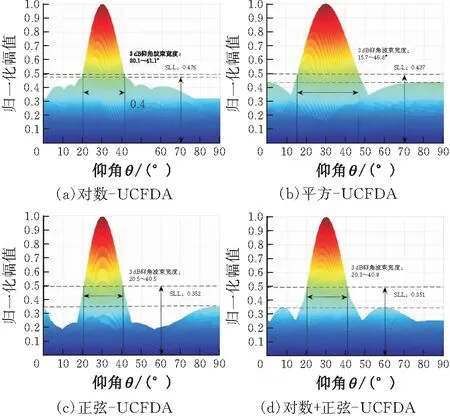
图6 仰角-距离维仰角的波束宽度

图7展示了log-UCFDA、square-UCFDA、sin-UCFDA、log+sin-UCFDA方位角-距离维关于方位角的波束特性。在方位角维，log-UCFDA的主瓣宽度为45.7°，旁瓣级为0.518；sin-UCFDA的主瓣宽度为34.6°，旁瓣级为0.457。log-UCFDA的旁瓣级最高。sin-UCFDA的主瓣宽度最窄，但旁瓣级较高，log+sin-UCFDA可以减小log-UCFDA的主瓣宽度，可以降低sin-UCFDA的旁瓣级。

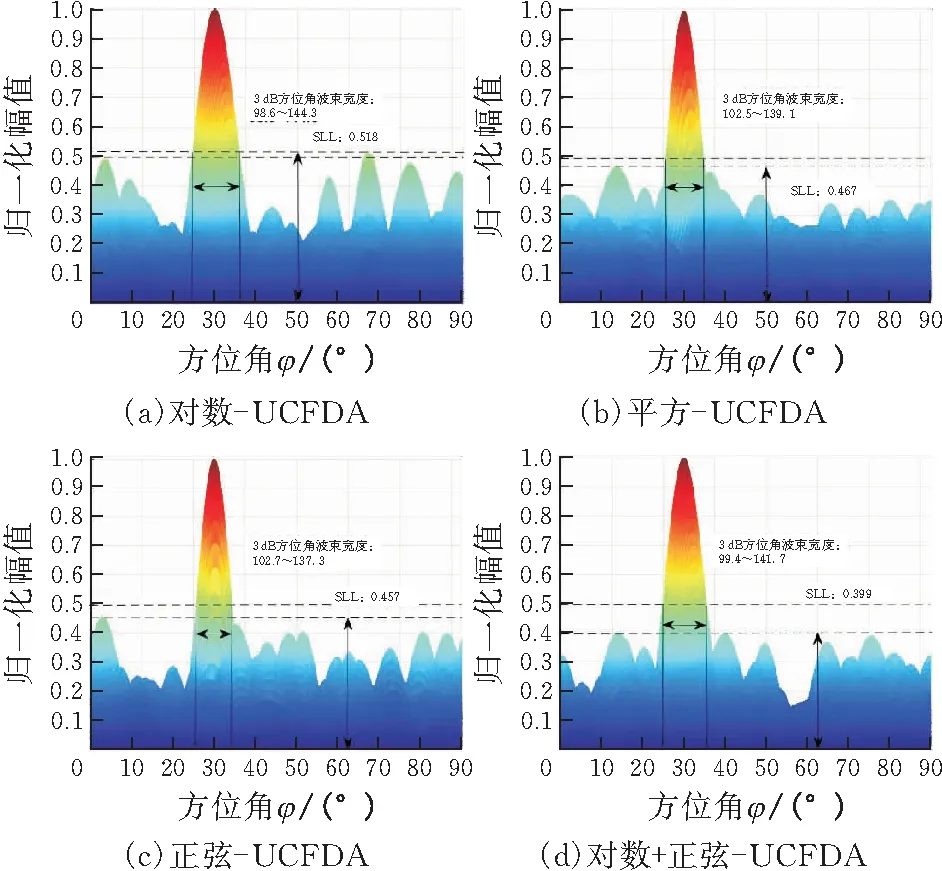
图7 方位角-距离维方位角的波束宽度

图8展示了log-UCFDA、square-UCFDA、sin-UCFDA、log+sin-UCFDA仰角-距离关于距离的波束特性。在距离维，四种频偏UCFDA的主瓣宽度都很窄，可以明显的看到log-UCFDA主瓣两边有较多旁瓣，表现在仰角-距离维平面图上距离维的“拖尾”波束，这不利于目标位置的定位。

图8 仰角-距离维〗距离的波束宽度

图9展示了log-UCFDA、square-UCFDA、sin-UCFDA、log+sin-UCFDA方位角-距离维关于距离的波束特性。在距离维，四种频偏UCFDA在目标位置都能形成很窄的主瓣，但同时在其它位置形成了增益较高的旁瓣，这些旁瓣是无规则的，并不依附在主瓣旁，表现在方位角-距离维平面图上方位维不规则能量聚焦点状亮点。

图9 方位角-距离维距离的波束宽度

表2 UCFDA关于不同方案频偏的距离、仰角的波束主瓣和旁瓣宽度

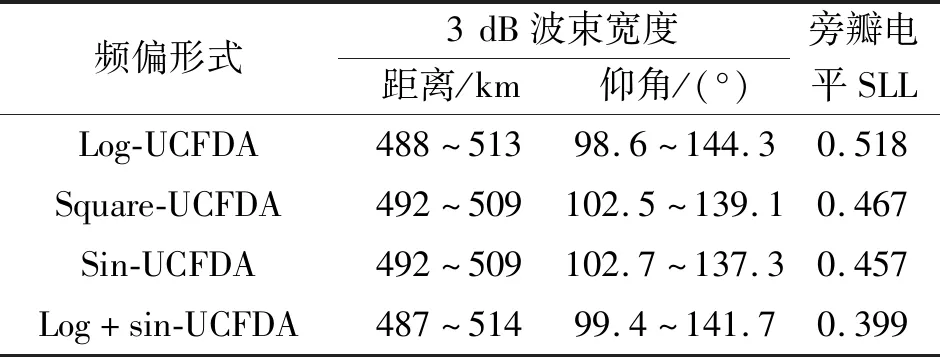
表3 UCFDA关于关于不同方案频偏的距离、方位角的波束主瓣和旁瓣宽度

4 结论

均匀圆阵提高了均匀线性频控阵的自由度,在分析UCFDA阵列结构的基础上，推导了基于线性频偏的频控阵发射信号处理模型；而后构建四种非线性频偏函数，提出了基于非线性频偏的圆型频控阵发射信号处理模型。得到结论：与线性频偏相比，提出的四种非线性频偏能解决距离和角度的耦合问题，且具有较高的主瓣分辨率。log+sin-UCFDA旁瓣级最低，square-UCFDA点状效果最好，sin-UCFDA的主瓣宽度最小。综合考虑距离、仰角和方位角的主瓣波束宽度、旁瓣数目、旁瓣电平、波束能量分布等多项因素，应选择满足相对应的频偏。