直流能馈型交流PEL的仿真研究
2020-10-27黄世元孙得金
黄世元,孙得金
(1 湖北工业大学 电气与电子工程学院,湖北 武汉 430068;2 武汉征原电气有限公司,湖北 武汉 430012)
交流PEL因其空间小、负载形式灵活、调节方便等优势常用于逆变电源的老化实验中。其常采用负载模拟+能量回馈两级结构,负载模拟单元用于模拟不同类型的负载,能量回馈单元根据回馈电能的类型分为交流能馈和直流能馈,目前交流PEL多为交流能馈型,采用PWM逆变器将能量回馈至电网,但该方式需要在并网侧添加大体积的工频变压器,导致整机体积庞大,使用不便。直流能馈型PEL能够将能量直接回馈至逆变电源的输入端,避免能量经多次转换造成的浪费,且移相全桥电路可以实现电气隔离。本研究PEL采用直流能馈。
负载模拟单元常采用电压型PWM整流器(VSR)。VSR为非线性系统,传统的PI控制无法满足负载模拟单元高性能的要求,因此,非线性控制成为研究热门。文献[1]通过分解网侧电流,实现解耦控制,控制性能较好,但存在参数调试复杂、大范围稳定性不强的缺点。文献[2]基于坐标变换,提出了引入前馈解耦和电流前馈补偿的方法,在一定程度上抑制了网侧电压的波动。文献[3]通过分解网侧电流,再设计无源控制器,提升控制性能。文献[4]采用定频滞环控制,无需载波,实现简单,对电路参数的依赖性低,通过改变控制电路实现开关频率固定,但影响系统的动态响应。文献[5]提出内环为反馈线性化解耦控制的方法,提高了动态性能。在上述文献基础上,本文将无源控制用于交流PEL,因篇幅有限,主要对负载模拟单元展开研究,能量回馈单元采用双环PI控制。
1 主电路结构
图1为直流能馈型PEL拓扑结构,前级为单相VSR,后级为移相全桥电路,前后级通过大电容连接,提高系统稳定性并实现前后级控制解耦。能量回馈单元将能量回馈至逆变电源的输入端。

图1 主电路结构
2 负载模拟单元的数学模型
负载模拟单元的主电路见图2。其中us为电源电压,L为交流侧电感,Rs为线路等效电阻,C为母线电容,udc为母线电压。

图2 负载模拟单元拓扑
单相VSR的数学模型为:
(1)
单相系统无法直接进行旋转变换,故采用滞后90°法构建正交向量来构造虚拟电流向量,从而可得d-q与α-β坐标变换式:

(2)
将式(2)带入式(1)中可得:
(3)
3 负载模拟的PCHD模型
系统的总能量存储函数
(4)
其中
x1=Q=Cudc,x2=Ψ1=Lid
x3=Ψ2=Liq
为实现能量控制,用x1/c、x2/L、x3/L代替udc、id、iq,由(3),可得
(5)
将其写成PCHD方程形式为:
(6)
其中,
式(6)即为单相VSR的PCHD模型。
4 负载模拟单元的控制器设计
4.1 VSR的无源性判断
在将无源控制应用于单相VSR前,先要判断VSR是否具有无源性。
若系统的能量存储函数满足不等式:
(7)
则系统严格无源。M(x)为任意正定函数,∀t>0。
将数学模型(3)变为
(8)
联立该方程组,可以得到
(9)
继续变换左侧可得
(10)

(11)
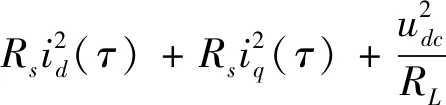
4.2 期望点的确定
期望稳定平衡点为:
根据功率平衡关系可算得idref:
(12)
其中,Um为输入电压幅值,IL为负载电流。
4.3 无源控制器的设计
利用IDA-PBC控制规律确定出使系统在期望平衡点处具有最小的能量Sd、Sq:
(13)
式中,Jd=J+Ja、Rd=R+Ra、Hd(x)=H(x)+Ha(x),Ja、Ra和Ha(x)分别为注入的互联矩阵、阻尼及能量函数,本文选取:
则式(13)变为:
(14)
令∂Ha(x)/∂x=K(x)=(k1k2k3)T,式(14)亦可写成如下形式
(15)
由(15)的第2、3个方程可得对应的开关函数:
(16)
由式(16)可知,该控制器中的参数较多,使用时设计较复杂,为简化控制器设计,取ra2=ra3=ra,ra1=0,同理,设k1(x)、k2(x)、k3(x)均为x1的函数,根据可积性有:
该式可等效为:
(17)
即k2=A2,k3=A3,A2和A3为待定常数。
为实现在xref处Hd有极值,需满足:
则可以得到
(18)
(19)
由开关函数(19)可以得到系统的控制框图,如图3所示。

图3 控制框图
对于Hd(x),由式(13)可得:
(20)
由式(20)可知,注入阻尼越大,系统响应速度越快,但过大的注入阻尼,会导致THD较大,合适的注入阻尼可通过仿真选取。
5 仿真实验与分析
在Matlab中进行仿真,根据以上设计搭建模型,负载模拟单元仿真参数:电源电压380 V,50 Hz,交流侧电感2 mH,线路等效电阻0.02 Ω,直流母线电容5600 uF,直流侧电压额定值600V,额定功率17 kW,开关频率8 kHz。能量回馈单元仿真参数:滤波电容1000 uF,滤波电感1.5 mH,谐振电容10 nF,隔直电容25 uF,高频变压器1∶1.5。不同注入阻尼的仿真见表1,考虑输入电流的THD,由结果可知当取ra=120时效果较好。

表1 不同注入阻尼的仿真结果
5.1 稳态性能
5.1.1 纯阻性负载在额定功率下,输入电流有功给定值63.3 A,无功给定值0 A。由图4a可知,输入电压和输入电流同相,无相位误差,输入电流峰值为63.8 A,与给定值相差0.5 A,误差小于0.8%。由图4b可知,稳定后,并网电流平均值为28 A,与根据功率平衡算得的理论值基本一致,电流纹波峰峰值最大值为8 A。

(a)输入电压、电流
5.1.2 阻容性负载模拟阻容性负载的仿真结果如图5所示,给定阻抗角为30°,即输入电流有功给定值为54.6 A,无功给定值为-31.5 A,输入电流超前了输入电压1.65 ms,转换为角度为29.7°,相位误差为1.0%,输入电流峰值为63.8 A,幅值误差小于0.8%。

图5 模拟阻容性负载
5.1.3 阻感性负载模拟阻容性负载的仿真结果如图6所示,给定阻抗角为45°,即输入电流有功给定值为44.8 A,无功给定值为44.8 A。由图6可知,输入电流滞后了输入电压2.5 ms,转换为角度为45°,相角差为45°,无相位误差,输入电流峰值为63.8 A,幅值误差小于0.8%。

图6 模拟阻感性负载
5.2 动态性能
5.2.1 负载突增在模拟纯阻性负载工况下,先以一半额定负载运行,1 s后突增为额定功率17 kW运行,仿真结果如图7所示。由图7可知,在1 s时发生负载突增,输入电流峰值由32.7 A突增为63.8 A,输入电流的幅值误差较小,相角差为0,突变后,输入电流经过0.002 s即可跟踪上给定值。

图7 负载突增仿真
5.2.2 负载突减与负载突增仿真类似,在模拟纯阻性负载工况下,先以额定功率17 kW运行,1 s后突减为一半额定负载运行,仿真结果如图8所示。由图8可知,输入电流峰值在1s时,由63.8 A突减为32.7 A,与理论值基本吻合,突变后,经过0.002 s即可跟踪上给定值。

图8 负载突减仿真
5.2.3 相位突变在额定功率情况下,电子负载的阻抗角由阻容30°突变为阻感45°,仿真结果如图9所示。由图9可知,电子负载先以阻容30°负载运行1 s,之后突变为阻感45°负载,输入电流经过0.002 s即可跟踪上给定值,完成相位突变,动态性能较好。

图9 相位突变仿真
5.3 对比仿真
由图10可知,无源控制下的输入电流THD为1.00%,PI控制下的THD为2.49%,对比文献[10],采用重复控制时,输入电流THD为1.56%,采用无源控制时THD更低。

(a)无源控制
6 结语
为提高交流PEL的性能,对于负载模拟单元,设计了一种基于PCHD模型的无源控制器,对于能量回馈单元,采用直流能馈提高能量利用率。通过仿真验证,在该控制下的直流能馈型交流PEL,负载模拟的稳态误差小、响应速度快、THD小。但是,由图4b可以看出回馈侧纹波含量较大,对能量回馈单元的性能优化还有待进一步研究。
