基于主成分分析和CNN 的图像分类算法研究

罗 斌 韩纪东

（1、赣州市肿瘤医院信息科，江西 赣州341000 2、北京工业大学信息学部，北京100124）

1 概述

卷积神经网络（Convolutional Neural Networks, CNN）是一种非常重要的图像处理技术，也是深度学习（Deep Learning,DL）领域最具有代表性的方法之一。卷积神经网络在图像中有着非常广泛的应用，如图像分类[1]、图像分割[2]、目标识别[3]等。随着技术的发展，卷积神经网络甚至已经被应用到了自然语言处理(Natural Language Processing, NLP)领域[4]，如文本纠错、命名实体识别、机器翻译等。

随着人们对模型的精度要求越来越高，卷积神经网络模型也被设计的越来越深，所需要的数据也相应的呈指数级增长。与之相对应的是，训练卷积神经网络的的难度也越来越大：

（1）对所需硬件要求越来越高，如性能更高且价格更昂贵的GPU、TPU 等；

（2）训练的时间也越来越长；

（3）训练所需的能源消耗也越来越大。为了解决这个问题，本文使用主成分分析（Principal Component Analysis，PCA）提取图像的主要信息，实际也就是对图像进行降维，然后再输入卷积神经网络；此时训练卷积神经网络时的计算及使用BP 算法进行参数更新时的计算会大幅下降，进而缩短卷积神经网络训练所花费的时间，也降低了训练卷积神经网络的硬件要求与能源消耗。

2 基本理论

2.1 主成分分析

主成分分析方法是一种经典的基于统计学的特征提取方法。深度学习技术兴起之前，曾被广泛应用于数据的特征提取，由于其性能优异，在图像人脸识别等方面得到了大量的应用。

大量数据相互之间通常会有一定的相关性，这说明了一个重要的问题，即大量数据所包含的信息具有一定的冗余。这就为我们提供了想法，使用一种算法剔除数据之间的信息冗余，这也就是主成分分析方法的目的。数据经过主成分分析方法处理后，变成彼此之间不相关的数据。

这里以图像为例，说明主成分分析方法的实现。主要有以下几个步骤：

（1）计算所有图像的协方差矩阵Cov；

（2）计算步骤1 中协方差矩阵Cov 的特征值、特征向量；

（3）将步骤2 中所得到的特征值按由大到小的顺序排列，并将特征值相对应的特征向量以同样的顺序排列构成变换矩阵；

（4）将步骤3 得到的变换矩阵与原始图像做矩阵乘法运算，结果即为经过主成分分析处理后的结果。

2.2 CNN

卷积神经网络具有非常强大的提取图像特征的能力。现在，卷积神经网络模型的使用方法主要有以下几步：

（1）提出需求，如人脸识别、行人检测、医学图像中的病灶部位（肿瘤等）分割等；

（2）收集大量的数据，现在的卷积神经网络是以数据为驱动的有监督学习，需要使用大量的数据训练模型；

（3）根据需要设计相应的卷积神经网络模型，卷积神经网络的主要基本单元有卷积运算、池化运算、批归一化或层归一化、线性层、随机丢失参数（dropout）、softmax 层等组成；4)将数据输入卷积神经网络训练模型。

3 模型

输入图像进入卷积神经网络后主要有两个运算：

（1）前项运算forward；

（2）反向传播BP。

由于训练的过程是类似于循环，显然，这两步将随着输入图像大小的增加产生大量的运算。使用PCA 降维后，不仅提取了图像的主要信息，而且尽最大可能保证了后续卷积神经网络的输入图像的完整性，同时也使得图像数据量变小。

图1 是本文设计的模型图。输入图像首先经过PCA 降维处理，降低图像的数据量，又能尽可能保证图像自身所携带的信息量。然后经过卷积块运算以提取特征。在本文中，该卷积块又可分为两个小卷积块conv1 和conv2。conv1 卷积块包含1 个卷积运算，1 个批归一化BN，1 个激活运算（使用ReLU 函数激活）；conv2 与conv1 设计的完全相同。图像经过卷积块运算后会有1 个池化运算，该运算实际是一种降采样。模型的最后一层为线性层，该层实际是一个分类器；经过线性层后实际还有一个softmax 运算，这里将softmax 隐性包含在了线性层中。模型的最终输出为图像的类别数。

4 实验

4.1 实验数据及实验条件

本文实验使用了Fashion-MNIST 数据集，该数据集共有70000 张图像，其中训练集60000 张，测试集10000 张；该数据集 共 有10 类，分 别 为'T-shirt/top'、'Trouser'、'Pullover'、'Dress'、'Coat'、'Sandal'、'Shirt'、'Sneaker'、'Bag'、'Ankle boot'，每一类有训练图像60000 张，测试图像1000 张；该数据集中的图像均为28*28 的灰度图像。

本文使用的硬件CPU 为intel Core i7，GPU 为NVIDIA GeForce RTX2060。

图1 模型结构图

4.2 实验结果

在实验中'CNN'表示原始卷积神经网络，即输入的图像没有使用主成分分析技术预处理。输入图像经过主成分分析技术预处理后图像的大小变为N*N，在本实验中N 的值分别取14、16、18、20、22，处理后图像的大小比原数据集中的图像28*28 明显小很多。

表1 和表2 分别表示使用原始卷积神经网络和使用主成分分析技术预处理后卷积神经网络准确率和时间消耗对比。由表1 可以看出N 取值为14、16、18 时准确率是在不断上升的，这符合本实验的预期；因为随着N 越大说明使用主成分分析技术预处理后得到的图像信息就更多更全。当N 取值为20、22 时准确率却在下降，这反而另本实验比较有意义，这提示N 的取值是有一个临界值的，当N 超过这个临界值时，使用主成分分析技术处理后的图像可能已经不适应卷积神经网络。由表2 可以看出，使用主成分分析技术后，卷积神经网络的训练时间明显缩短。在本实验中，N 取16 或18 是一个比较综合的结果，兼顾了准确率与训练时间。

图2 是分别训练30 轮、40 轮、50 轮的损失值下降曲线对比图。结合表1 观察图2，可以发现两者是极其吻合的，表1 中N取16 或18 时准确率非常接近；图2 中N 取16 或18 时两者的损失函数值极其接近，在图2 中两者几乎重合。这也从另外一个角度说明本文实验的正确性。

表1 准确率对比

表2 时间对比

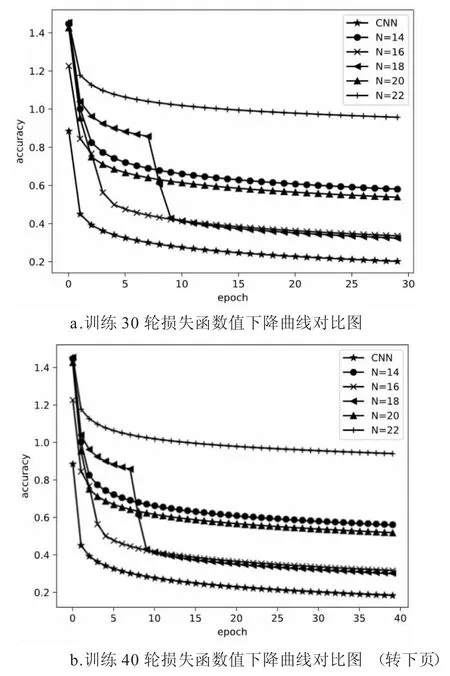
图2 分别训练30 轮、40 轮、50 轮的损失值下降曲线对比图

5 结论

由实验结果可以看出，图像先通过主成分分析方法处理，然后再输入到卷积神经网络，可在略微损失准确率的条件下大幅降低训练卷积神经网络的时间。在准确率要求不是那么严格的条件下，本文使用结合主成分分析技术与卷积神经网络的方法还是非常可取的。本文方法依然有不足之处，由实验可以看出N 的取值对训练结果的准确率及时间消耗都有非常的的影响；下一步，我们的研究重点将放在，探索出一种方法以方便取N 最优值。