基于离散元法的分段螺旋式TMR搅拌机搅龙结构对混合性能影响研究
2020-10-26王凯飞温宝琴阿依肯叶留拜李利桥李景彬
■王凯飞 温宝琴,2* 阿依肯·叶留拜 张 杰,4 李利桥,2 李 洋 李景彬,2 坎 杂,2
(1.石河子大学机械电气工程学院,新疆石河子832000;2.现代农业机械兵团重点实验室,新疆石河子832000;3.新疆维吾尔自治区农牧业机械管理局信息中心,新疆乌鲁木齐830001;4. 新疆农业科学院农业机械化研究所,新疆乌鲁木齐830001)
全混合日粮(Total Mixed Ration,TMR)搅拌机是对一定比例的粗精饲料进行搅拌混合后制成全混合日粮的装备[1-2],具有效率高、操作简便的特点,适用于规模化养殖场,目前TMR搅拌机在国内外已经得到广泛应用。
近年来,国内外专家学者针对搅拌机的混合性能展开了诸多研究,如Dennis R等[3]、刘江涛等[4]、郭庆贺等[5]针对单轴、双轴卧式搅拌机,利用示踪剂对其混合性能进行评价。物料在搅拌机内部的运动过程极其复杂,通过理论分析和物理试验虽然可以进行物料组分分析,但是对搅拌机内部颗粒的运动规律缺乏直观描述。而离散元法(Discrete Element Method,DEM)自提出以来在颗粒运动分析方面得到了迅速发展,GR Chandratilleke 等[6]利用离散元法对混合机中的叶片前角展开研究,表明前角为135°时,在装置顶部和底部颗粒分散度最大。王德福等[7]对装置内颗粒的运动轨迹进行追踪,进而对其运动特征进行分析,表明桨叶安装角对颗粒运动速度影响较大。桂泽东等[8]利用离散元法分析了V 型混料机内部两种颗粒的运动情况,并对V 型筒壁夹角进行了优化,结果表明V 型筒壁夹角为60°时混合速率更优。以上研究表明搅拌装置不同结构对颗粒在其内部的运动、扩散规律具有显著影响。目前利用离散元法对比不同结构参数下装置混合性能已经进行了诸多研究,但对于分段螺旋叶片不同排布形式下对装置的混合性能研究还较少。
本文以分段螺旋式TMR 搅拌装置为载体,借助离散元软件EDEM,建立物料离散元模型,开展混合过程数值模拟研究,探究轴向对称和中心对称分段螺旋叶片排布的不同搅龙对物料的作用规律,以混合均匀度和转矩为指标,通过分析相同工况下两种结构的混合均匀度和转矩动态变化过程,对比其混合性能差异,得出较优工作结构参数,为优化设计分段螺旋式TMR搅拌机奠定基础。
1 模型的建立
1.1 整机结构与工作原理
分段螺旋式TMR 搅拌机的整机结构如图1 所示。工作过程中由电动机提供动力,利用分段螺旋式搅龙做顺时针圆周运动,带动物料做空间立体运动,实现物料的混合装置技术参数如表1 所示。分段螺旋搅龙是主要工作部件之一,由搅龙轴管、分段螺旋叶片、梅花刀片、搅龙堵头、紧固螺栓等组成,其结构对装置的混合性能影响较大,构建分段螺旋叶片在搅龙上呈轴向对称和中心对称两种排布方式的分段螺旋式搅龙,如图2所示。

图1 分段螺旋式TMR搅拌机

表1 分段螺旋式TMR搅拌机参数

图2 不同排布方式分段螺旋搅龙
1.2 物料模型的建立
本文选用呈秆状的玉米秸秆,呈块状的玉米秸秆破碎后皮穰,呈球状的玉米面作为此次仿真混合物料原型,为提高计算效率,对模型进行优化,采用5 mm半径小球进行多球面填充的方式建立与之对应的离散元颗粒模型,如图3所示。物料材料属性参数根据前期实验基础及于克强[9]、郭庆贺[10]相关研究按照表2的数据进行设置。
1.3 接触模型的建立

图3 物料离散元模型
本文的研究涉及大量物料之间的混合作用,物料在装置内部的运动形式复杂,存在大量物料与物料、物料与装置之间的相互接触碰撞,其碰撞力计算复杂且计算量庞大,本文通过求解牛顿运动方程来获得每个颗粒的旋转和平移运动,如式(1)、(2)所示,并在每个时间步长上对颗粒的速度和位置进行数值整合,进而更新颗粒的速度和位置,如图4所示。

表2 仿真物料特性

图4 颗粒运动计算

式中:I——转动惯量(kg·m2);
ω——角速度(rad/s);
M——作用在颗粒上的接触力矩(N·m);
t——时间(s)。

式中:v——颗粒的平移速度(m/s);
m——颗粒的质量(kg);
fg——作用在颗粒上的重力(N);
Fc——颗粒与颗粒之间的接触力(N);
Fnc——颗粒与装置之间的接触力(N)。
为考虑颗粒与颗粒、颗粒与装置之间的接触,本文选择计算精度和效率都较高的Hertz-Mindlin 接触模型[11-12],其法向力基于Hertz 接触理论,切向力基于Mindlin 切向接触计算方法,并在法向力和切向力上分别引入阻尼分量,切向遵循库伦摩擦定律,将滚动摩擦视为定向恒定转矩模型,如图5 所示,并设置其接触参数如表3 所示,同时结合图3 所示的不同物料离散元模型,若颗粒与颗粒或颗粒与装置之间产生接触,则根据接触的位置和颗粒状态利用接触模型计算出作用在颗粒上的力,并利用上述牛顿方程和数值积分进行计算,得出颗粒的加速度、速度和位置情况,在每个时间步下进行同步求解。其计算过程如图6所示。
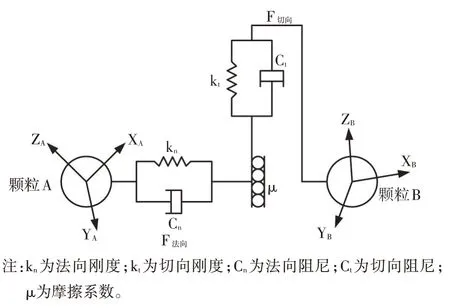
图5 Hertz-Mindlin接触模型

图6 DEM计算过程
2 离散元数值模拟结果分析
在Solid Works软件中对装置进行简化,保留壳体及搅龙部分,将文件另存为IGS格式,并导入EDEM离散元软件中进行计算。设置搅龙从0 s开始转动,将搅龙转速设置为和实际工况一致的30 r/min,转动20 s,时间步长1.26×10-6s,利用EDEM软件中的一个叫“颗粒工厂工具”依次动态生成6 000 个秆状颗粒标记为黄色、6 000个块状颗粒标记为绿色、15 000个球状颗粒标记为红色,使其受重力作用下落至壳体内,进而在搅龙的作用下运动。

表3 接触参数
2.1 混合过程分析
如图7 所示,为不同时刻的颗粒混合剖面图。图7在0 s时装置开始转动,颗粒开始生成,在1.6 s时颗粒生成完毕,并下落到壳体内,此时颗粒分为上中下三层,其中下层和中间层秆状和块状颗粒由于先于球状颗粒生成,在搅龙作用下发生轻微的混合作用;在3.5 s 时颗粒在搅龙作用下发生运动,在壳体两端的颗粒受搅龙作用开始向中间运动,同时由于分段螺旋叶片之间存在间隙,颗粒也通过叶片之间的间隙进行移动,此时混合过程中剪切混合和扩散混合是主要的混合形式;在8 s时刻,此时大部分颗粒被输送至中部,形成堆积,并沿其堆积角回落,形成对流混合,此时剪切混合、扩散混合和对流混合三种混合形式共同作用于物料,且对流混合是主要混合形式,并随着时间的推移混合均匀度逐渐上升;在14 s 时,随着时间的推移,在三种混合机制的作用下,颗粒的位置不断移动,颗粒逐渐达到混合均匀的状态,并在随后的时间内不断交换位置,导致混合均匀度发生波动。
2.2 颗粒运动矢量分析
为对颗粒在两种搅龙作用下的运动情况进行更直观的观察分析,将颗粒显示模式设置为矢量模式,其箭头所指方向为颗粒受力运动方向,体积大小和颜色由红色到蓝色表示运动速度的快慢。
如图8 所示,在12~13 s,此时颗粒在轴向对称分段螺旋搅龙的作用下,由两端向中部位移,位移到中部的颗粒在中间部分对称分段螺旋叶片的作用下进行周向运动,其中中下部物料受其叶片阻挡,汇聚在搅龙中部,不能进行左右位移,运动方向垂直向下,且部分堆积在中间区域,另外一部分则在轴向对称搅龙的夹持作用下继续进行圆周运动;而中上部颗粒,由于未受到叶片影响,以较快速度向两侧扩散,进入搅龙内,在搅龙下一圈运动时随搅龙往中部移动;与之对应时刻的中心对称搅龙,由于其结构形式的不同,物料在分段螺旋叶片之间进行整体轴向移动,且位移方向与颗粒所在位置所靠近的螺旋叶片旋向保持一致。
2.3 颗粒混合均匀度分析
混合均匀度是指各种原料在外力作用下混合的均匀程度,会随混合时间的变化而产生变化。为了对在两种结构作用下的颗粒混合均匀度进行量化分析,将计算区域划分为10×6×6=360 个网格区域,对每个网格内的每种颗粒数量进行统计。为保证研究的准确性,去除颗粒量小于30个不具有统计意义的网格,通过对每个网格区域内每种颗粒数量占该区域颗粒总量的百分比及每种颗粒总数占总颗粒量的百分比情况,将此视为最佳混合均匀度;再将每个网格区域的每种颗粒的占比与最佳占比进行比较,将此视为混合均匀度的偏离情况,计算混合均匀度偏离情况的标准差,为混合均匀度偏离系数。偏离系数越大,颗粒混合越不均匀,反之则混合越均匀,其混合均匀度数学模型如式3所示[13-14]。

式中:n——网格数量(个);
xi——颗粒i数量占该网格总颗粒量比例(%);
Xi——颗粒i的全部颗粒量比例(%)。
将两种搅龙不同时刻的颗粒数量数据导出,并根据式(3)计算其偏离系数,并绘制其随时间变化曲线,如图9所示。图9在0~2 s,偏离系数在初期颗粒未完全生成时处于较低水平,待颗粒完全生成,偏离系数达到较大值;在2~10 s,偏离系数值急剧下降;在10~14 s,偏离系数下降逐渐趋于平缓,但仍然存在一定的下降趋势;在14 s时,偏离系数达到较低水平,并在随后的时间内趋于平稳状态,但仍存在上下波动。
究其原因是因为仿真开始时颗粒还处于较少阶段,即使在不运动的情况下,颗粒对于此时存在的全部颗粒也相对均匀,待颗粒生成完毕,偏离系数达到峰值,此后颗粒在搅龙的带动下不断运动混合,混合均匀度升高,偏离系数随之减小,并呈现出一定的线性关系;在第10 s时,混合均匀度达到较高水平,增长开始放缓,但在搅龙的作用下物料之间仍然存在相互运动,彼此交换位置,所以仍然存在混合均匀度上升,偏离系数下降的趋势;在第14 s时混合均匀度达到最优,此时颗粒在壳体内部均匀分布,但是随着搅龙的继续转动,颗粒仍然存在运动,导致偏离系数上下波动。

图7 不同时刻颗粒运动状态
对比两种搅龙偏离系数发现,轴向对称搅龙在2~8 s时刻,偏离系数低于中心对称搅龙;在8~14 s时刻,中心对称搅龙偏离系数低于轴向对称搅龙,在14~20 s 时刻两种搅龙都存在上下波动情况,但总体来看,两种搅龙的偏离系数趋于一致,差异性较小。以上结果表明在混合初期,轴向对称搅龙由于其轴向对称结构原因,颗粒存在轴向输送的同时,径向夹持输送的能力也较强,所以混合初期轴向对称搅龙的混合效率较高,而随着时间的推移在中心对称搅龙的影响下,颗粒之间的对流混合和扩散混合作用逐渐加强,其混合均匀度超过轴向对称搅龙,致使偏离系数低于轴向对称搅龙,但是整体来看,两种搅龙混合效率基本一致。
2.4 装置转矩数值分析

图8 颗粒运动矢量图
转矩是机械部件转动所需的力矩值,其数值能够直观反映出装置能耗大小,且与装置工作性能、寿命、安全性能等密切相关。不同结构下的转矩大小及平稳性可以反映出其结构形式不同而导致的工作状态不同,对比出结构的优劣,对装置的优化设计具有重要意义。分段螺旋搅龙在工作过程主要进行回转运动与物料颗粒发生作用,其转矩消耗主要来自对物料混合过程中的输送、剪切和自身回转运动的消耗。两种搅龙工作过程中的转矩随时间变化如图10(a)所示,为了更清晰的描述转矩动态变化趋势,对数据进行FFT滤波处理,处理后曲线如图10(b)所示。分析结果表明:轴向对称搅龙呈现出增大后趋于平稳的趋势,中心对称搅龙呈现出先增大后减小再增大进而趋于平稳的趋势。将工作过程分为3 个阶段:0~3 s,此时搅龙刚开始转动,颗粒刚落入料箱内,搅龙刚开始输送颗粒,颗粒还未形成堆积,输送量较小,此时转矩处于较小值;3~6 s,此时壳体中部物料逐渐开始增多,对于中心对称结构搅龙,在每次转动输送颗粒时,由于其中心对称结构,在搅龙每转一圈时,单侧螺旋叶片需要克服另一侧螺旋叶片在前半圈输送来的物料,所以所需的转矩呈现显著增大趋势,但对于轴向对称搅龙,由于前期壳体中部所存在的颗粒量较少,且搅龙中部两块呈现对称结构的螺旋叶片会对物料产生夹持作用,使颗粒随搅龙一起转动,所以搅龙转矩与前期基本保持一致;6~20 s,此时物料颗粒被搅龙完全输送至中部造成堆积,物料颗粒依靠重力进行回落,搅龙接触颗粒数量随之较少,轴向对称搅龙在每圈转动时对物料产生的剪切作用明显,且在中部形成的堆积更陡峭,中部两块呈现对称结构的分段螺旋叶片,共同作用于物料,致使其所需转矩急剧增大,且波动振幅更大,对于中心对称搅龙,由于其在转动时,物料整体产生轴向位移,其物料与物料之间产生的应力能够得到释放,故所需的转矩呈缓慢上升趋势,并在达到稳定后呈现小范围波动。

图9 混合均匀度偏离系数随时间变化

图10 转矩随时间变化
对其转矩数值进行对比发现,轴向对称排列搅龙在第12.9 s 时达到转矩峰值为2 849.62 N·m,在工作过程中转矩平均值为1 478.51 N·m,四分位距为1 872.50 N·m;中心对称排列搅龙在5.4 s时达到转矩峰值为1 768.34 N·m,工作过程中转矩平均值为866.65 N·m,四分位距为432.74 N·m。将数据进行对比分析可知,相较于轴向对称搅龙,中心对称搅龙,转矩峰值降低37.94%,转矩平均值降低41.38%,四分位距减小76.89%。其中转矩峰值的降低有利于装置整机作业能耗的降低;平均值的降低和四分位距的减小,表明中心对称搅龙在转矩方面相对于轴向对称搅龙在工作过程中转矩动态波动范围更小,工作过程中有更好的稳定性和可靠性。
3 结论
①提出轴向对称和中心对称排列的两种分段螺旋式搅龙,对其混合过程进行剖面和矢量对比分析,表明混合前期主要是剪切混合和扩散混合,后期主要是对流混合;在轴向对称搅龙影响下的颗粒汇聚在中部,由中部向两侧扩散;在中心对称搅龙影响下的颗粒进行轴向整体位移。
②对混合均匀度和搅龙转矩进行量化分析,结果表明,在两种搅龙的混合效率较为接近的情况下,中心对称搅龙相较于轴向对称搅龙转矩峰值降低37.94%,转矩平均值降低41.38%,四分位距减小76.89%,采用中心对称结构可以显著降低搅龙工作峰值转矩,提升装置运行平稳性。
本文在研究过程中利用离散元技术对复杂的混合过程进行了分析,由结论可知,本研究可以丰富搅拌装置的研究手段,为优化设计分段螺旋式TMR搅拌机奠定基础,对提高搅拌机工作性能具有参考意义。
