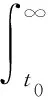二阶半线性阻尼微分方程的振动准则

罗红英, 俞元洪

(1. 曲靖师范学院数学与统计学院, 云南 曲靖 655011; 2. 中国科学院数学与系统科学研究院, 北京 100190)

(r(t)φα(z′(t)))′+p(t)φα(z′(t))+q(t)φβ(x(σ(t)))=0

(1)

的振动, 其中z(t)=x(t)+c(t)x(τ(t)),φn(s)=|s|n-1s,α和β是正数．显然, 方程(1)是文献[3]的重要推广．

1 预备知识

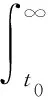
证明 在方程(1)两端乘E(t),得

(R(t)φα(z′(t)))′+E(t)q(t)φβ(x(σ(t)))=0,

(2)

则(R(t)|z′(t)|αz′(t))′≤0, 故z′(t)最终定号, 即z′(t)>0或z′(t)<0．若z′(t)<0, 则存在T>t0．

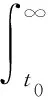
证明 i) 若β≥α, 则w′(t)≤-Q(t)-βσ′(t)R-1/α(t)z′(σ(t))(z′(t))-1(z(σ(t)))(β-α)/α·w(α+1)/α(t)．由(R(t)(z'(t))α)′≤0, 知R(t)(z′(t))α是减函数, 故R(t)(z′(t))α≤R(σ(t))·(z′(σ(t)))α．由引理1知z′(t)>0, 则有z′(σ(t))/z′(t)≥(R(t)/R(σ(t)))1/α．因z(t)是增函数, 则对于t≥T>0, 有(z(σ(t)))(β-α)/α≥(z(σ(T)))(β-α)/α．

令M1=min{1,(z(σ(t)))(β-α)/α}, 则w′(t)≤-Q(t)-βM1σ′(t)R-1/α(σ(t))w(α+1)/α(t)．又R′(t)≥0,R(σ(t))≤R(t),故

w′(t)≤-Q(t)-βM1σ′(t)R-1/α(t)w(α+1)/α(t)．

(3)

ii) 若α>β, 则w′(t)≤-Q(t)-βσ′(t)R-1/β(t)(z′(t))-α/βz′(σ(t))w(β+1)/β(t)．由于(R(t)·(z′(t))α)′≤0, 可得z″(t)<0, 即z′(t)是减函数, 则对于t≥T,有

w′(t)≤-Q(t)-βM2σ′(t)R-1/β(t)w(β+1)/β(t),

(4)

其中M2=min{1,(z′(T))1-α/β}．综合式(3) (4), 令M=min{M1,M2},λ=min{α,β}, 有w′(t)+Q(t)+A(t)w(λ+1)/λ(t)≤0, 其中A(t)=λMσ′(t)R-1/λ(t)．

2 主要结论

本文假设:

1)r(t)∈C1([t0,∞),R+),c(t)∈C1([t0,∞),R),r′(t)≥0, 0≤c(t)≤1;

3)σ(t)∈C1([t0,∞),R),σ′(t)>0,σ(t)≤t, limt→∞σ(t)=∞;

4)p(t),q(t)∈C([t0,∞),R+)．

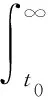
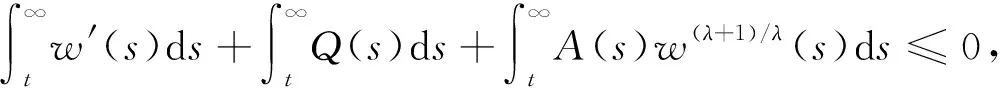
ε-ε0ε(λ+1)/λ>1．

(5)

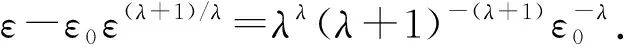
下面用Philos型积分平均给出定理2．考虑集合D={(t,s):t≥s≥t0},D0={(t,s):t>s≥t0}．函数H(t,s)∈C(D,R)称为属于D类, 记作H(t,s)∈X, 满足: ①H(t,t)=0,t≥t0;H(t,s)>0, (t,s)∈D0; ② ∂H(t,s)/∂s≤0, 且存在ρ∈C1(I,R+)和h∈C1(D0,R), 使得∂H(t,s)/∂s+ρ′(s)·H(t,s)/ρ(s)=-h(t,s)Hλ/(1+λ)(t,s), (t,s)∈D0．

定理2设H∈X．存在ρ∈C1(I,R+),h∈C1(D0,R), 使

(6)

则方程(1)振动．

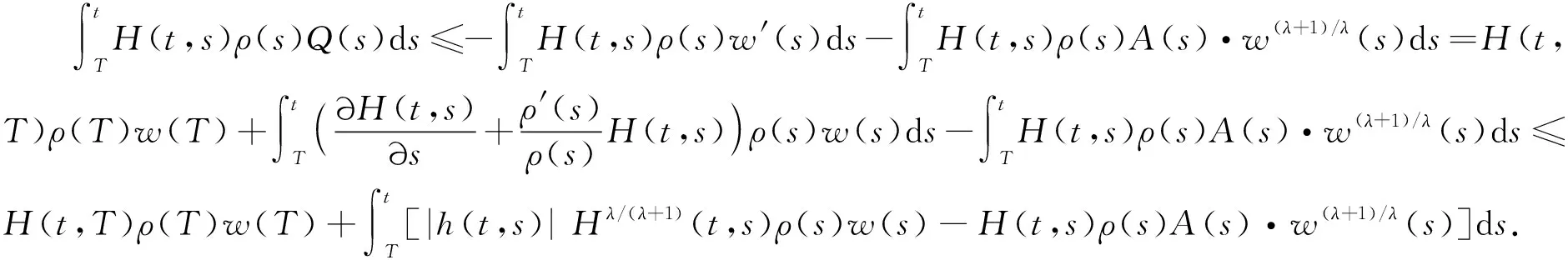
3 应用