超网络中心性度量的υ-Position值方法
2020-10-24单而芳彭超婧
单而芳, 蔡 蕾,2, 曾 晗, 彭超婧
(1.上海大学 管理学院,上海 200444; 2.上海市第一人民医院,上海 200080)
0 引言
在各种政治、经济、社会等网络中,我们常常需要识别出其中相对重要的成员,也就是网络中的关键节点。例如作为网络防护方来说,识别出网络中的关键节点后可以对一些关键节点进行备份,或采取其他手段对其进行保护,这样就能大幅度的提高整个网络的鲁棒性和抗毁性。再例如目前生物学领域的大量研究证实蛋白质分子的功能大小与它在复杂生物网络拓扑结构中的重要性有着紧密联系。因此识别出生物网络中关键的蛋白质分子,对于疾病诊断、病毒研究等生物信息领域能起到关键作用。此外,在政治网络如国际组织中,若能识别出对组织最重要的成员并投入相对多的关注和资源,对于该组织的稳定性和发展都将大有裨益。因此,如何度量网络节点的重要程度,发掘出关键节点具有重要的理论与应用价值。
目前,已有文献中提出的关键节点的识别方法主要有两类: 一类是经典的中心性测度方法,主要基于节点在网络结构中的位置。这需要充分挖掘网络结构的信息,从中寻找有用信息来反映节点在结构中的显著性。例如在某一星状通讯网络中,中心节点与其他每个节点都直接相连,所以它拥有的连接度是最大的, 因此可以认为它是该网络中的中心节点。根据这一思想而提出的中心性测度方法主要有:特征向量测度、度值测度、紧密测度、中介测度等方法[1,2]。这些方法侧重网络的结构,其共同的不足是较少能应用于网络中对政治和经济现象的解释。另一类中心性的测度方法是利用合作博弈理论的收益分配规则。主要有两种: Banzhaf值法[3]和Shapley值法[4]。这些方法通过分析某一点的边际贡献或者该点失效后的后果来衡量其重要性。与侧重网络结构的中心性测度方法不同的是合作博弈理论能够考虑到政治经济因素、博弈的情境和参与者的权重。然而此类方法由于忽视合作的结构,而假设任何联盟都是可行的,从而很可能无法准确描述网络中各参与者的中心性。例如,在某些政治、经济或社会背景下, 参与者的权重决策机制是不合理的, 因为在这些环境中, 联盟的规模有时并不具有决定性的意义。 另一方面, 如果参与者之间存在互不兼容性, 那么Shapley值法是不适用的, 特别在政治网络情境中,一旦两个政党之间的意识形态存在互不兼容, 那么所有潜在的由双方参与的政府组织都将不会产生。为了避免这个缺陷,Myerson[5]在考虑合作结构的前提下,借助Shapley值提出了一种新的分配规则,也就是Myerson值。Myerson值以图或者超图(也就是网络或者超网络)作为合作结构,用图中的节点表示参与者,图中的边来表示参与者之间的直接交流关系,并假设不连通的参与者之间不能形成可行联盟。不过,Myerson值虽然考虑了网络结构对中心性的影响,但侧重突出网络中参与者(节点)的作用,而把每条边的地位和作用当作是一样的。
然而,在现实中参与者之间联系的紧密性、交流深度和合作程度有可能是不一样的。为了描述此类情形,除了考虑以边赋权图为合作结构外,1988年, Meessen[6]提出图博弈中另一个重要的分配规则, 也就是Position值。它是首先将图博弈中的每条边看成“参与者”,计算出每条边的Shapley值[7], 然后把每条边的Shapley值平均分配给它的两个端点代表的参与者, 给每个参与者的支付(payoff)等于与它关联的所有边Shapley值一半的和。Borm等[8]给出了无圈图博弈上Position值的唯一性刻画,并讨论了Position值的计算公式。van den Nouweland等[9]进一步把Position值推广到超图结构中,并把Borm等在无圈图博弈上Position值的刻画结果推广到无圈超图博弈上。2005年, Slikker[10]终于在任意图博弈上证明了Position值能够被分支有效公理和平衡边贡献(balanced link contributions)公理所唯一刻画。2003年,Gómez等[4]在考虑社会网络中心性和指数时,首次尝试利用图博弈中的Position值。最近,Belau[11]在Gómez等工作的基础上,把图博弈中Position值的概念推广为广义Position值作为衡量网络中心性的标准,并讨论了它的性质刻画和应用。关于Position值的其他研究进展参见[12~14]。
近年来,超图(hypergraph)作为超网络的拓扑结构越来越受到关注。它是图的一个自然推广,在现实中是普遍存在的。例如,每个人可能会参加各种各样的团体、协会和组织,这些人和国家可以看作参与者,而所在的团体、协会和组织可以看作超图中的超边(conference或者hyperlink)。不过,由于在超图中,每个超边由一些节点形成的子集所组成,不像图中每条边恰有两个节点所形成,因此在超图结构上的合作博弈其情形更加复杂。本文旨在推广Belau[11]的思想,提出超图博弈中的广义Position值,这里称为“υ-Position”值,并给出其公理化刻画。从而为超网络的中心性度量提供经济意义上的理论方法。
本文的组织如下: 第二节给出超图博弈的基本定义和记号。第三节提出超图博弈υ-Position值的概念和新的公理——局部平衡超边贡献,并给出υ-Position值中“类Shapley-Position值”的公理化刻画。最后举例说明υ-Position值在超网络中心性测度中的应用。
1 预备知识
1.1 TU-博弈
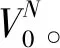
对于博弈(N,υ),一个支付向量(payoff vector)x=(x1,x2,…,xn)∈Rn是指分配给第i个参与者的支付为xi。TU-博弈的单值解(single-valued solution)或者值(value)是一个映射f:VN→Rn,表示指派给每个(N,υ)的一个支付向量f(N,υ)∈Rn。这个值就是通常所说的分配规则(allocation rule)。对于给定的参与者集合N和一个非空联盟T⊆N,一致性博弈(unanimity game)(N,uT)[7]定义为:若T⊆S,则有uT(S)=1;否则,有uT(S)=0。已经知道:任意一个博弈(N,υ)的特征函数都能唯一表示成一致性博弈的线性组合[15],也即有
(1)
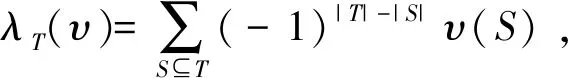
(2)
1.2 超图和超图博弈
作为图的自然推广,超图(hypergraph)[9]由二元组(N,H)所组成,其中N表示节点的集合,H⊆HN={e⊆N:|e|≥2}表示至少含有两个节点的超边(hyperlink)集合。显然,当每条超边e满足|e|=2时, 超图即为普通的图。如果N是明确的,通常用H代表超图(N,H)。Hi为H中包含节点i的超边的集合, 也即Hi={e∈H|i∈e}。节点i的度(degree)deg(i)定义为|Hi|。
在超图H中,若i∈e,则称节点i与超边e∈H是关联的;如果存在一条超边e∈H满足i,j∈e,则称节点i和j是邻接的。一条长度为k的路(path)是指一个点边交替序列(i1,e1,i2,e2,…,ik,ek,ik+1),这里i1,i2,…,ik+1是不同的节点,e1,…,ek是H的不同超边,且对每个1≤l≤k,il,il+1∈Hl。如果超图H中任何两个节点i,j之间均存在路,则称H是连通的。对于任意非空集合S⊆N,(S,H(S)),称为由节点集S导出的子超图,其中H(S)={e∈H|e⊆S}。若H(S)是连通的,则称S是H的一个连通子集。H的一个极大的连通子集称为它的分支,记H所有分支的集合为N/H。 特别地,T/H(T)表示由T导出子超图的分支集合。为了方便起见, 有时记T/H(T)为T/H。
超图博弈(hypergraph game或者hypergraph communication situation)可以用一个三元组(N,υ,H)来表示,其中(N,υ)是一个TU-博弈,而(N,H)是一个超图。此时,超图的节点集N表示参与者的集合。H中每一条超边e可表示一个conference结构[9]。在实际中,超边可以代表某种社会组织如:行业协会、企业集团或者政治团体等,每个参与者可以参加多种行业组织或企业集团,并参与不同联盟的合作。
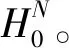
以下分别记TU-博弈和超图博弈分配规则的集合为A和AH。
1.3 超图博弈的Position值
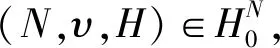
(3)
由于0-规范博弈与对应的非0-规范博弈具有策略等价性,同时为了避免计算的繁琐,在以下的讨论中,除非特别说明,涉及的博弈均指0-规范的TU-博弈。其他未定义的概念和记号可参考[18]。
2 υ-Position值
从1.3小节超图博弈Position值的定义可知,Position值是借助超边博弈的Shapley值定义的一类分配规则。事实上,我们这里也可以用其他值(如Banzhaf值[19])来替代(3)中的Shapley值,并得到相应的位置值。基于这个考虑,我们可以定义超图博弈上的一类广义Position值。
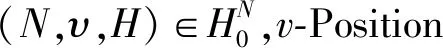
(4)
显然,由定义可知:当v=Sh时,上述v-Position值即为普通的Position值。
正像前面指出的,在度量网络中心性时,节点的度是考察其中心性的最基本方法之一。事实上,我们可以通过定义“权度”,将这个方法推广到赋权图或者赋权超图上。
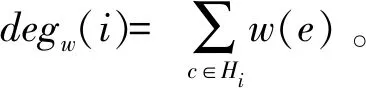
按照上述定义,可以根据每个节点权度的大小来衡量该节点的中心性。事实上,在某种意义上,v-Position值可作为度测度的一个推广。
命题1在超网络节点的中心性度量中,v-Position值是一类“权度”测度。
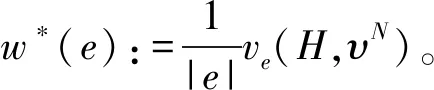
为了深入讨论和刻画v-Position值,注意到Shapley值和Banzhaf值的共性,我们把讨论的分配规则限制在类Shapley值的范围内。把A中满足下列几个基本性质的分配规则集合记为A*,也即对每个v∈A*,满足下列四个性质:
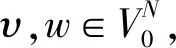
(ii)对称性(S):若i,j∈N且对任意的S⊆N{i,j}满足:υ(S∪{i})=υ(S∪{j}),此时称i和j是对称的,则vi(N,υ)=vj(N,υ);
(iii)哑元非相关性(NI):若i∈N且对任意的S⊆N{i}满足:υ(S∪{i})=υ(S),此时称i为哑元,则有vi(N,υ)=0且对任意的i≠j∈N,vj(N,υ)=vj(N{i},υ);
(iv)单值性(U):v能被唯一确定。
我们已经知道,在合作博弈中,有许多值如Shapley值和Banzhaf值等均满足上述性质。下面我们的讨论主要集中在A*上进行。当v∈A*时,此时由于v-Position值是基于具有Shapley值和Banzhaf值共性的分配规则给出的,因此也把它称为“类Shapley-Position值”。
3 “类Shapley-position值”的公理化刻画
本节将给出超图博弈上“类Shapley-Position值”的公理化刻画。为了符号简便,当参与者集合N明确时,经常书写时省略N。
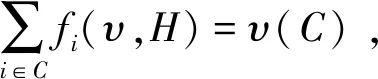
分支有效性是说每个分支内的所有参与者的支付之和等于该分支的效用,这个性质强调节点的贡献。仿照此思想,为了强调图博弈中边的贡献,Belau[11]提出了一个性质公理,被称为分支超边指数。这里把分支超边指数性质推广到超图博弈上。
分支超边指数(Component Hyperlink Power,简记为CHP),假设v∈A,对任意的(N,υ,H)∈HN及任意的C∈N/H,若分配规则f∈AH满足
(5)
则称f具有对应于分配规则v的分支边指数性质。
这个性质的含义是: 超图博弈(N,υ,H)中,对某一分支的支付等于该分支中在分配规则v下所有超边的支付之和。
根据定义可以证明下列结果:
引理1对于任意超图博弈(N,υ,H)∈HN及v∈A,πv∈AH满足分支超边指数(CHP)性质。
证明假设C∈N/H,注意到每条超边e恰好贡献|e|个度,根据(4)可得:
从而得证。
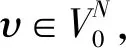

则称f满足平衡超边贡献。
不过, 对超图博弈中的Position值进行刻画时,平衡超边贡献性质是失效的。需要用到下列“部分平衡超边贡献”性质[20]:
部分平衡超边贡献(partial balanced hyperlink contributions,简记为PBHC):对任意超图博弈(N,υ,H)∈HN和i,j∈N,若分配规则f∈AH满足
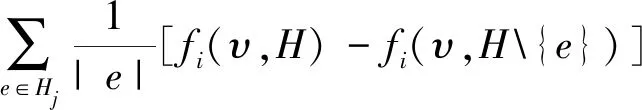
(6)
则称f具有部分平衡超边贡献性质。
部分平衡超边贡献性质可解释为:去掉包含参与者i的每条超边对参与者j收益的平均影响的和等于去掉包含参与者j的每条超边对参与者i收益的平均影响的和。明显的, 若将超图(N,H)限制为一般图(N,L)时, 局部平衡超边贡献公理即为平衡边贡献公理。
为了证明超图博弈(N,υ,H)∈HN的v-Position值满足分支超边指数和局部平衡超边贡献这两个公理, 首先, 根据一致性博弈, 给出以下引理。
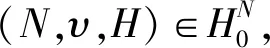
证明因为每个博弈的特征函数都可以写成其对应的一致性博弈的线性组合[18]。因此,对于超图博弈(N,υ,H),对应的超边博弈υN可以表示为:
(7)
首先,注意到对每个e∈HK及任意T⊆H{e},有uK(T∪{e})=uK(T),因此e是一个哑元。所以对每个e∈HK,ve(H,λK(υN)uK)=0。因为v∈A*,由v值的性质NI可知:ve(H,λK(υN)uK)=ve(K,λK(υN)uK)。其次,注意到对任意的e,e′∈K及T⊆K{e,e′},有uK(T∪{e})=uK(T∪{e′})=0,也即e和e′是对称的,则由v值的性质S可知:对任意的e,e′∈K,有ve(K,λK(υN)uK)=ve′(K,λK(υN)uK),或者等价于,对任意的e∈K,有ve(H,λK(υN)uK)=ve(K,λK(υN)uK)=c(υ,v,K),根据v值的对称性S和单值性U,这里c(υ,v,K)∈R是一个只依赖于υ,v,K的常数。进一步,根据v值的可加性A及(7),我们有
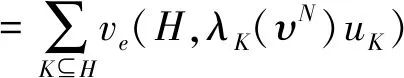
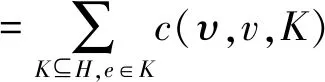
因此,我们有
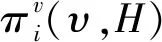
其中Ki=K∩Hi。令Kj=K∩Hj,于是有,
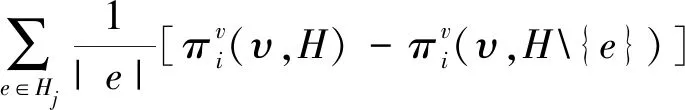
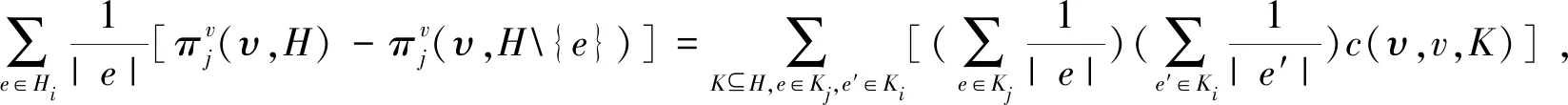
现在给出本文的主要结论。
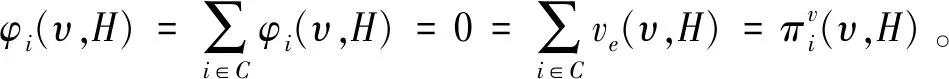
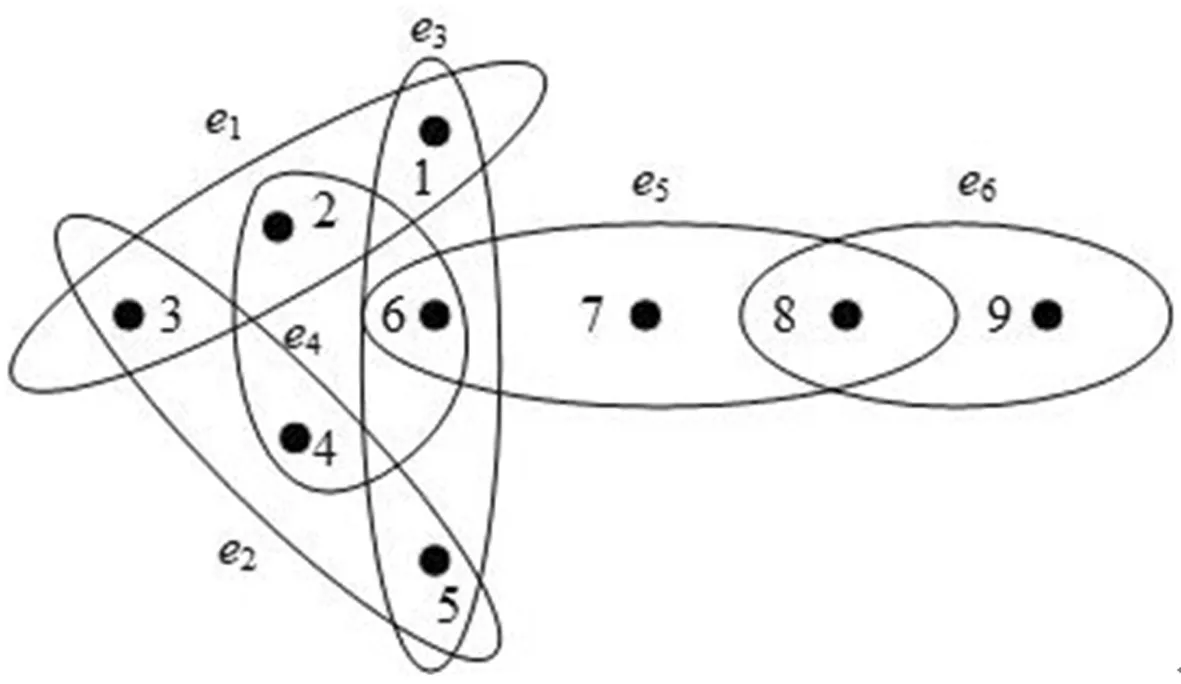
现在假设对任何超图H,当|H| 根据上式,对分支C内的所有节点做和,则得 (8) 因为φ满足CHP性质,因此根据引理1,由(8)式的左边可得: (9) 同理,由(8)式的右边可得: (10) 本节通过Shapley-position值和Banzhaf-position值,举例说明v-Position值的性质和它在超网络中心性测度中的应用。 例1某经济网络,其经济学模型可抽象为超网络博弈(N,υ,H)∈HN,其中参与者集合为N={1,2,…,9},超边集为H={{1,2,3},{3,4,5},{5,6,1},{2,4,6},{6,7,8},{8,9}},特征函数为υ=uN,如图1所示。设e1={1,2,3},e2={3,4,5},e3={5,6,1},e4={2,4,6},e5={6,7,8},e6={8,9}。 图1 超图(N,H) (11) (12) 我们验证Shapley-position值和Banzhaf-position值分别满足性质CHP和PBHC。注意到超图H是连通的,也就是恰好只有一个分支。由上面的计算结果,容易验证: 因此这两个值满足部分平衡超边贡献性质。 下面分析Shapley-position值和Banzhaf-position值在度量超网络H节点中心性时的一些特点。由超图H的结构,容易计算各个参与者的度值分别为: deg(i)=2,i=1,2,…,5,8 deg(6)=3;deg(7)=deg(9)=1 (13) 根据(11)~(13)式可得表1。 表1 各个参与者在三个值中所占的比例. 由表1,我们发现用度值来度量时,其度值最大的为参与者6,也就是参与者6在位于最中心的位置或者说为“top关键节点”,其次度值相对较大的是参与者1,2,…,5,8,它们为可看作“次关键节点”,而参与者7和9为最不重要的节点。 不过,在用Shapley-position值和Banzhaf-position值进行度量时,情况发生了很大变化。此时,参与者8的值最大,它成为“top关键节点”,而参与者6为“次关键节点”,而且参与者6在这两个值中具有相同的比例值,也就是说中心性相同。在Shapley-position值中,参与者1,2,…,5成为最不重要的节点,而在Banzhaf-position值中,参与者7成为最不重要的节点。注意到参与者9在Shapley-position值测度中,其中心性提高显著。其原因是在用Shapley-position值和Banzhaf-position值进行度量时,凸显了超边e5,e6作为中介的重要性,因为它们的任意一条被删掉,网络的连通性立即被破坏,而删掉其他超边e1,e2,e3,e4其中一条时,网络仍保持连通。所以Shapley-position值和Banzhaf-position值测度体现了“超边”作为桥梁的作用,而不是仅考虑节点的结构位置关系。 在现实生活中,选择不同的分配方法,可以体现决策者不同的分配意图。例如,在企事业单位内部的绩效奖金分配过程中,决策者如果单纯从某个部门或个人联系面的广泛性入手进行分配,那么那些交际面广泛、在公共关系中发挥较大作用的部门或个人就能够获得较多的绩效分配;但是,如果从单位内部整体运转的不可或缺性着手,那么在整个部门协同机制中发挥关键连通作用的部门将获得较多的绩效分配。从绩效奖金分配推而广之,这三种不同的分配方法还能够广泛用于资产、资源的评估过程,因为资产或资源的评估建立在标准的价值计算模型上,而任何价值计算都有一定经济学意义上的“偏向性”,因此,在评估时选取何种分配方法进行计算,将显著体现出评估的目的取向性——是偏重于资产或资源的位置值还是偏重于它们的战略地位,从而计算得出的价值是不同的。 本文讨论了超网络中心性测度的一类方法——广义Position值(v-Position值)方法,用此类方法来度量时,既突出了“超边的经济作用”,又考虑了其结构关系,而传统的度值等方法主要从节点所处的位置来考虑。另外,通过分支超边指数和部分平衡超边贡献两个性质,给出了类Shapley-position值的唯一性刻画。注意到网络博弈(图博弈)是一类特殊的超图博弈,此时每条边恰有两个元素,这导致在图博弈中部分平衡超边贡献性质会退化为平衡边贡献性质,因此本文结果蕴含了一般网络上的相关结论。在超网络博弈中,当一条超边被增加或者删掉时,是否每个参与者都会受益或者受损?这就是超边单调性问题,该问题对合作的稳定性具有重要影响。一般来说,这个问题的答案是否定的。那么到底超网络博弈满足什么条件就具有超边单调性是需要进一步深入研究的问题。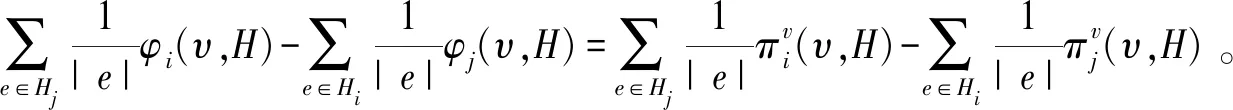
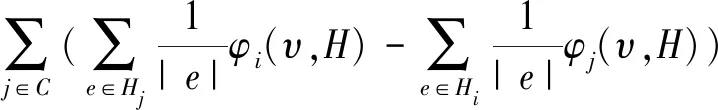
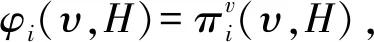
4 υ-Position值在超网络中心性测度中的应用举例
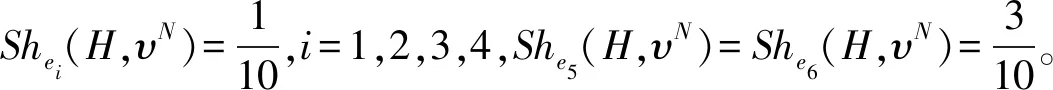
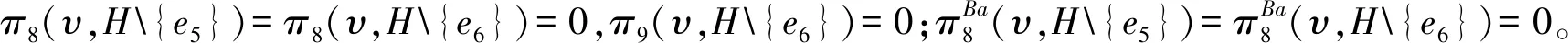

5 结论及注记
