化工园区应急设施区间规划选址模型研究

2020-10-24郭换换王飞跃裴甲坤杨宸宇

运筹与管理 2020年5期

郭换换, 王飞跃, 裴甲坤, 杨宸宇

(1.中南大学铁道学院防灾科学与安全技术研究所,湖南长沙 410075; 2.济宁市安全生产技术服务中心，山东济宁 272000)

0 引言

化工园区危险源集中，一旦发生事故对人员生命和经济破坏是巨大的。合理的应急设施选址布局对减轻突发事件后果损失具有重要的作用。近年来，多目标应急设施选址模型理论和方法的研究在多方面得到了广泛的应用，如城镇公共服务设施选址[1,2]、自然灾害应急设施选址[3]等，但对于化工园区应急设施选址的研究及应用很少。化工园区危化品事故性质与自然灾害不同，化工园区内危险工艺集中、危险源种类性质繁杂，加大了化工园区突发事件发生的不稳定性和复杂性。因此，为满足园区在发展过程中不断变化的应急服务的需求，实现园区应急救援效率的最大化，研究化工园区不确定条件下的应急设施规划选址问题尤为迫切。

早期对设施选址问题的研究有三种经典的类型：P-中值问题[4]、P-中心问题[5]和覆盖问题[6,7]。这些经典的设施选址研究都假设设施存在严格的覆盖半径，但是这种严格覆盖半径的假设在许多实际情况下是不合理的[8.9]。后来，基于经典的设施选址研究成果，国内外越来越多的专家学者[10,11]展开了对应急设施选址进一步的研究。但由于实际突发事件的复杂性，应急设施选址中存在很多不确定性的影响因素，因此，近年来针对不确定性的研究成为了国内外学者关注的热点问题。如王飞飞等[12]通过引入交通满意度及道路受损风险系数两个变量，构建了基于多属性满意度的复杂地形乡镇地区应急设施选址模型。基于突发事件应急救援设施故障不确定的问题，An等[13]建立了随机混合整数非线性规划模型；张敏等[14]建立了基于设施故障情景的评估指标体系和应急设施选址模型。基于应急需求不确定性，陈刚等[15]引入概率分布和三角模糊数，建立了应急供应链的多目标选址规划模；Murali等[16]基于距离敏感度的需求不确定性的考虑，建立了大规模生物袭击下的应急设施最大覆盖选址模型。彭春等[17]同时考虑应急需求与运输成本的不确定性，建立了非线性鲁棒设施选址模型，并将其转化为混合整数线性规划模型计算。基于突发事件时间的不确定性，俞武扬等[18]提出了应急服务时间、风险最小化的应急设施选址模型；Lutter等[19]利用鲁棒优化的方法建立了混合整数线性规划模型，分析了应急设施的选址问题。

综上述，目前对基于不确定条件下的应急设施选址的研究成果有很多，主要集中于随机规划、模糊规划和鲁棒优化，但这些研究成果在建模中普遍存在以下的问题：(1)基于情景分析方法研究不确定参数具有一定的局限性。突发事件具有很强的随机性，其发生地点、事件性质存在很大的差异，确定有代表性的灾害情景及灾害情境发生的概率比较困难；(2)通过搜集历史数据拟合不确定参数的概率分布函数具有一定的困难性。一般情况下很难搜集到同一地区大量类似突发事件的相关历史数据，因此通过搜集相关历史数据拟合预测不确定参数的概率分布函数分析不确定性是一项很庞大的工作。另外，通过以上研究成果发现，目前针对化工园区应急设施选址的研究涉及很少，且鲜有学者将应急设施选址点潜在的风险大小即安全性考虑在建模内。因此，本文基于前人的研究，以化工园区各企业潜在事故为背景，在化工园区应急设施选址点一定风险控制水平的基础上，引入区间数表示应急物资需求参数的不确定性，引入模糊理论降低目标函数求解过程中的不确定性，建立了基于需求不确定条件下的多目标区间规划选址模型，对化工园区应急设施选址的优化布局进行研究。

1 模型建立

1.1 问题分析

应急设施作为灾区应急救援物资的主要支援点，其选址受多种因素的影响。一方面，合理的应急设施选址应该同时考虑到以下几点：(1)应急设施为需求点提供的服务质量要尽可能大，这样才能保证救援的质量；(2)应急设施只有在保证自身安全有效的情况下才能满足灾区基本的需求，这是应急设施选址需要考虑的基本因素；(3)考虑应急设施选址成本和事故损失之间的平衡，既不能浪费资源也不能让事故得不到救援，这就需要考虑应急设施建址成本和应急设施数量的选取问题。

另一方面，化工园区事故特征机理复杂加之事态紧急，灾区人员伤亡的统计不能及时、准确的获得，灾民对应急物资需求的种类和数量也不能被准确的计量，导致灾区应急物资的需求不是一个精确的值。如果应急物资供过于求，虽然可以将多余的应急物资进行再次储备，但此过程人力和物力的消耗是不可避免的；而如果应急物资供不应求，则事故应急救援效率就会降低，会造成更大的损失。因此，应急设施选址必须考虑灾区应急物资需求的不确定性，保证应急救援的效率。

综上述，本文对应急设施选址进行分析时，提出了同时考虑成本最小化、应急物资需求满足率最大化和设施选址风险最小化目标的基于需求不确定条件下的应急设施选址优化模型。建模假设条件如下：

(1)应急设施选址成本较大，一旦建立应急设施，则在较长时间内不再变动；

(2)由于灾害的突发性及时间的紧迫性，灾区应急物资需求量具有不确定性，但能根据灾区以往不同时间段的人口密度及受灾程度等信息预估得到物资需求量的区间值；

(3)所有应急需求点均能被应急设施所覆盖；

(4)每个应急设施选址点都具有一定的潜在风险且风险值各异；

(5)假设有足够的资金可供建址使用；

(6)突发事件中，应急车辆可正常通行。

1.2 模型建立与求解

建模中所用符号的意义：

①下标

i,(i=1,2…I) 应急设施选址点序号

j,(j=1,2…J) 应急需求点序号

m,(m=1,2…M) 应急物资种类数

k,(k=1,2…K) 应急设施的容量类型序号

②常量

ri应急设施选址点i处的潜在风险值

dij应急设施选址点i到应急需求点j的距离

ck建立第k种类型的应急设施所需要的固定成本

sk第k种应急设施的容量

um第m种应急物资单位数量的运输成本

Q(dij) 服务质量函数，定义了服务质量函数与距离的关系

L应急设施选址点的最大选取数量

③决策变量

yi为0-1变量，若在应急设施选址点i处建立应急设施则值为1，否则为0

xijm为0-1变量，若需求点j处对第m种应急物资的需求由应急设施选址点i提供，则取值为1，否则为0

zik为0-1变量，若在选址点i处建立第k种类型的应急设施，则取值为1，否则为0

④区间系数

由1.2建模参数的定义，建立应急设施多目标区间规划选址模型如下：

(1)

(2)

(3)

(4)

(5)

xijm≤yi(i=1,2,…,I;j=1,2,…,J;m=1,2,…,M)

(6)

(7)

(8)

zik∈[0,1],yi∈[0,1],ri≥0,sk≥0,xijm≥0

(9)

式(1)为服务效益目标函数，即应急设施为应急需求点提供的服务质量最大化；式(2)为应急设施选址风险最小化目标函数；式(3)表示应急设施选址成本最小化目标函数，应急设施选址成本包括应急设施的建址成本和应急物资的运输成本；式(4)为应急设施容量限制约束，即应急物资的需求量应不超过应急设施存储容量；式(5)表示一个应急设施可以同时为多个应急需求点提供服务；式(6)保证了只有在建立应急设施的情况下，该应急设施才能为应急需求点提供服务；式(7)表示在每个应急选址点处至多建立一种容量类型的应急设施；式(8)限定了应急设施选址点选取数量的上限；式(9)为变量及常量的非负定义。

由于应急设施选址点和应急需求点距离的不同，因此应急设施为应急需求点提供的服务质量也并非完全相同。一般情况下，距离越近应急物资到达需求点的时间越早，应急设施的服务质量越好。因此，本文对目标函数(1)中的服务质量函数Q(dij)的处理借鉴了渐进覆盖的思想，得到服务质量和距离之间的岭型函数关系如公式(10)所示：

(10)

其中dij为应急设施选址点与应急需求点之间的实际距离，s+和s-分别表示在一定的时间范围内应急设施能提供较优服务质量的最近和最远的临界距离。最近和最远的临界距离以公式s±=vt±为原理确定，v表示在灾区道路正常情况下，应急车辆的行驶速度，t-、t+分别表示突发事件应急物资赶到现场的最理想和最长的限制时间，服务质量Q(dij)(0≤Q(dij)≤1)。

以上应急设施多目标区间规划选址模型与一般的应急设施多目标规划选址模型有以下两点不同：①区间多目标规划模型目标函数和约束条件均含有区间参数；②区间多目标规划目标函数值是一个区间值，而不是一个精确的值。因此，本文对应急设施多目标区间规划选址模型的求解异于传统的应急设施选址模型的求解，采用了区间理论[20,21]对多目标区间规划模型进行转化。

1.2.1 多目标区间规划模型的转换

(1)目标函数的转化

(11)

则目标函数(3)可转化为：

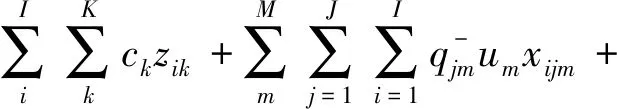
令lijm=gjmxijm,(0≤lijm≤xijm)，则有:

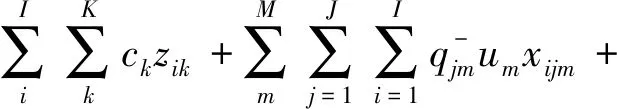
(12)

(2)约束条件的转化

(13)

由于目标函数值在求解过程中具有模糊性。因此，本文引入模糊理论，通过对目标函数建立相应的模糊隶属度函数降低求解过程中的不确定性，实现最大化的目标函数满意度，并使用模糊线性加权算法求解多目标规划模型。其求最大化目标函数Gk的模糊隶属度函数和求最小化目标函数Gl的模糊隶属度函数分别如下

(14)

(15)

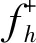
综上述，形成等价的应急设施单目标规划选址模型如下所示:

s.t.λfh≤(fh-minfh)/(maxfh-minfh)(h=1)

λfh≤(maxfh-fh)/(maxfh-minfh)(h=2,3)

(5)～(9)

其中wfh表示第h个目标函数的相对权重h=1,2…，λfh指每个目标函数的满意度水平，e表示三个目标函数满意度的总体实现水平。

1.2.2 模型计算步骤

多目标应急设施选址模型计算中，每个目标之间会相互制约使模型求解结果达不到最优化，甚至出现无解的情况。因此需要通过对多目标进行转化，寻找多目标应急设施规划选址模型的优化解。本文通过总结现有研究成果可知，目前对多目标优化模型的计算一般有两种途径：一是通过转化将多目标转化为单目标模型进行计算，其计算方法有三种：线性加权组合法、理想点法、主要目标函数法(也称epsilon约束法)；二是分层序列法，依次在前一个目标的约束下寻求下一个目标函数的优化值。以上两种求解途径的基本出发点多是基于对确定性的多目标规划模型进行求解，而本文建立的应急设施多目标区间规划选址模型加入了应急物资需求不确定性因素的考虑，模型在求解过程中具有模糊性。因此本文使用模糊线性加权算法对所建立的模型进行求解。模型的求解步骤如下：

(1)将多目标区间规划模型转化为等价的一般多目标规划模型；

(2)计算多目标区间规划模型的每一个目标函数的上下界值；

(3)计算每个目标函数的隶属度函数；

(4)将每个目标函数的隶属度进行加权，形成等价的单目标规划模型；

(5)利用模糊线性加权算法，通过计算机编程，寻求模型优化解。

2 案例应用

以湖南省某化工园区为背景，讨论园区内企业发生自然灾害事故时，园区应急设施(指应急物资储备库)的合理布局救援问题。已知该园区内有9家已全面运行的企业，包括制药类、建材类及石油化工类等一些存储重大危险性物质的企业。指定9家企业为潜在事故发生点(应急需求点)，编号为B1到B9。因突发事件具有随机性，事故地点、时间不确定，一旦园区某家企业发生事故，若救援不及时，事故损失将会扩大。因此为及时应对园区内突发事件，需要对园区应急设施选址进行规划，以便及时应对园区事故。通过综合分析评估，初步拟定在企业周围选取5处应急设施选址点做为候选点，并准备在此建立应急物资储备库，5处候选的应急设施选址点分别编号为A1到A5。位置分布如图1所示：

本文只考虑一种应急物资，即M=1。现已知的案例数据有：应急需求点与应急设施选址点之间的距离如表1所示；应急需求点应急物资的需求量如表2所示，其中需求量为区间数；根据该化工园区已有资料，利用模糊综评价法得到5处候选应急点处的潜在风险值如表3所示；根据专家打分法给出三个目标函数的权重分别为：wf1(服务质量)=0.4、wf2(选址安全性)=0.35、wf3(选址成本)=0.25；两种应急物资储备库的储存能力分别为sk=100和sk=150(吨)，每种应急物资储备库的建设费用ck分别为10和20(万元)；通过专家经验及相关资料收集确定单位物资的运输成本为u=0.023(每吨/万元)；决策者最终决定在该化工园区内选定最多3个应急设施选址点建立应急物资储备库，即L=3；本文选定的服务质量函数的距离临界值为[s-,s+]=[10,15]。

图1 化工园区潜在应急需求点与候选应急设施选址点分布图

表1 应急设施选址点到应急需求点的距离(km)

表2 应急需求点的需求量(吨)

表3 候选应急设施选址点的潜在风险值

由以上描述，建立等价的化工园区应急设施多目标规划选址模型(MOP)如下:

(16)

(17)

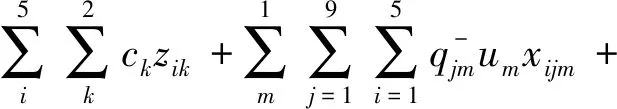
(18)

(19)

(20)

xijm≤yi(i=1,2,…,5;j=1,2,…,9;m=1)

(21)

(22)

(23)

zik∈[0,1],yi∈[0,1],ri≥0,sk≥0,

xijm≥0,0≤lijm≤xijm,vjm≥0

(24)

由以上数据，根据MOP模型计算得到每个目标函数值的上下界值如表4所示：

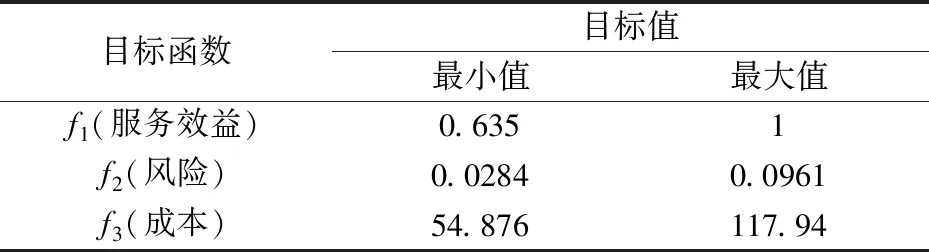
表4 目标函数值

计算各目标函数的隶属度函数为：

(25)

(26)

(27)

建立等价的单目标规划模型如下：

(28)

(29)

(30)

(31)

(32)

(19)

(20)～(24)

建模中，当lijm取0、vjm取1时，此时的模型为求最优最好解，即取最小成本、约束范围最大条件下的模型解；当lijm取1、vjm取0时，此时的模型为求最差非劣解，即最大成本、约束范围最小条件下的模型解。为计算方便，本文取lijm、vjm分别为统一的值，即取lijm为1、vjm为0，以求在最不利条件下模型的优化解。将以上算例数据代入单目标规划模型，通过计算机软件编程求解得到的结果如下，应急设施选址点选址方案如图2所示。

e=1.562,f1=1,f2=0.089,f3=89.474

y3=y4=y5=1，z31=z41=z51=1

x37=x38=x39=x41=x43=x44=x52=x55=x56=1

图2 化工园区应急设施选址方案分布图

结果显示，三个目标函数的总体满意度水平为1.562>1，表明目标函数的总体满意度实现水平较好；三个目标函数值分别为：服务质量为1，即100%、设施选址风险最小化的值为0.089、服务成本为89.474万元。最终的设施选址方案：选定A3、A4、A5三处应急设施选址点，并分别在这三个应急设施选址点处建立容量类型为s1=100吨的应急物资储备库。其应急物资分配方案为，若园区内企业B7、B8或B9发生事故，则优先选择A3处的应急储备库为其提供服务；同样，A4处的应急储备库优先为潜在事故点B1、B3和B4提供服务；A5处的应急储备库优先为园区内潜在事故点B2、B5和B6提供服务。