基于改进的粒子群算法求解供应链网络均衡问题

马 斌， 吴泽忠

(成都信息工程大学 应用数学学院，四川 成都 610225)

0 引言

供应链网络是一个复杂的动态系统，网络中成员的利益经常不一致甚至发生冲突，在各成员利益均能保证的基础上，探求供应链网络的均衡条件与实现系统总体的利益最大化的问题越来越受到重视。

Nagurney等人在2002年提出了供应链网络均衡模型[1]，研究了由制造商、零售商与需求市场组成的单商品流供应链网络均衡问题，提出可以将模型转变为变分不等式，通过修正投影法进行求解；Dong等人认为确定的需求不符合现实情况，于是在Nagurney研究的基础上，构建出更符合实际情况的随机需求供应链均衡模型[2]，该模型仍然通过投影算法得到最优解；由于修正投影法中步长与李氏常数的确定往往依赖经验，不同的参数值会对结果产生较大影响，而在求解非线性优化问题方面，拟牛顿法一直是最有效方法之一，Meng Q[3]与Zhang LP[4]分别用拟牛顿法与光滑牛顿法求解Nagurney提出的基础模型并将结果在精度与耗时两个方面做了对比。修正投影法与拟牛顿法在求解该问题时都存在各自的优势与缺陷，当供应链节点增多，网络结构相对复杂时，计算量会明显的上升，模型的求解速度也会变慢。本文作者也曾提出利用蜂群算法求解供应链网络[5]，相比传统方法较为简单，但其求解精度并不高。

心理学家Kenndy和电气工程师Eberhart通过模拟自然界鸟群、鱼群等生物相互合作，随机搜索找到食物的机制提出了粒子群优化算法[6]。由于其结构简单、需要调节的参数少，容易实现等优势受到研究者的广泛关注，并将其应用到了许多实际问题中。如Ramadan RM等人将改进的粒子群算法应用于人脸识别系统中[7]；原文林等人[8]将协同进化的粒子群算法用于求解比较复杂的高维梯级水库短期发电优化调度问题；韩毅等人[9]将其用于求解无能力约束生产批量计划问题中等。

但标准的粒子群算法容易陷入局部最优，难以适应复杂的非线性优化[10]，本文在此基础上提出一种动态调整学习因子的粒子群算法，并将其用于供应链网络均衡问题的求解，通过四个数值算例与标准PSO算法、同步变化学习因子的粒子群算法、蜂群算法[11]进行比较，结果显示，改进算法求解的精度高、收敛速度快，验证了改进的粒子群算法在供应链网络均衡问题求解的有效性与优越性。

1 确定需求下供应链网络均衡模型

该模型由顶层的m个制造商，中间层n个零售商以及底层的o个消费者组成。i,j,k分别代表每一层中具体的制造商、零售商以及消费者。

图1 供应链网络结构

制造商i向零售商j之间的产品发货量为qij，零售商j与消费者k之间的产品发货量为qjk，qij组成m×n维发货量矩阵Q1，qjk组成n×o维发货矩阵Q2。Cij表示制造商i与零售商j的交易成本(包含产品的运输成本)，每个制造商i面对一个生产成本函数，其依赖于整个向量的生产量，表示为fi。确定需求是指在需求市场k处消费者对商品的需求可以用dk(ρ3)表示，其中ρ3k表示在需求市场k处产品的价格，而ρ3表示需求市场价格的o维列向量。

假设生产成本函数、交易成本函数都是可微的。当制造商、零售商、需求市场同时达到最优时，整个供应链网络是均衡的。均衡状态下的变分不等式[1]为:

(1)

将其等价的改写为NCP问题，即寻找一个列向量

(2)

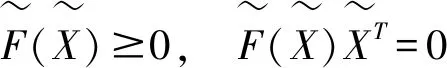
(3)

其中

(4)

(5)

(6)

(7)

(8)

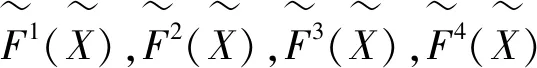
i=1,…,m;j=1,…,n

(9)

(10)

(11)

(12)

最后，我们通过价值函数[3]

(13)

该NCP问题可等价的转化为如下的无约束优化问题：

(14)

其中

(15)

2 动态调整学习因子的粒子群优化算法

2.1 标准粒子群算法

PSO算法作为人工智能算法的一种，其思想同其它智能算法一样，也是通过迭代更新来找到最优解。该算法将每一组解看作粒子，由给定的迭代策略不断调整粒子的位置，通过比较适应度函数的大小来判断其解的优劣程度。在迭代开始阶段，赋予每个粒子的随机的位置和速度，在搜索过程中，粒子自行判断与最优解的距离与方向，及时调整自己的速度和方向，以此寻找到最优解。PSO算法更新速度、位置的公式如下:

Vi(t+1)=ωVi(t)+c1r1(Pi-Xi(t))+

c2t2(Pg-Xi(t))

(16)

Xi(t+1)=Xi(t)+Vi(t+1)

(17)

其中i=1,2,…,n；ω是惯性因子；c1c2为学习因子，通常取2；r1,r2是介于[0,1]之间的随机数；Pg为全局最优位置；第i个粒子的位置Xi=(xi1,xi2,…,xin)，速度为Vi=(vi1,vi2,…,vin)，自身的最优位置Pi=(Pi1,Pi2,…,Pin)。

2.2 动态调整学习因子

在粒子的搜索过程中，每个粒子在每一次位置更新后，都将通过评价函数来判断当前解的优劣程度，及时调整当前的位置与速度，以便找到最优解。自身的信息与群体的信息可以通过两个学习因子来控制，而两个随机数增强了群体的多样性。若学习因子缺少变化，容易导致粒子陷入局部最优。Suganthan[12]提出将c1、c2进行相同速率的改变，其采用的方式为同速率线性递减，即

(18)

该方法不断的同步改变学习因子取值来改善优化的结果。而本文考虑到认知部分和社会部分对算法的不同影响，即(16)式的第二部分与第三部分在不同时期对算法的影响应该是不同的，随着迭代次数的增加，粒子的全局搜索能力应该增强，局部探索能力适度减弱，这样改动使算法初期具有较强的开采能力，后期不至于陷入局部最优解，平衡了算法的局部开采与全局寻优能力。综上所述，c1,c2分别采用线性递减与线性递增策略，改进如下:

(19)

(20)

2.3 算法步骤

采用改进的粒子群算法求解供应链网络问题步骤如下：

Step1赋予粒子群初始的随机位置和速度；

Step2将(15)式作为该算法的适应度函数，计算每个粒子适应度值Ψ1；

Step3将每个粒子的当前的适应值与其所经历的最好位置的适应度值Ψpbest作比较，若当前的值更好，进行替换，并记录最好位置pbest；

Step4将每个粒子的适应值与所有粒子经历的最好位置Ψgbest作比较，若当前的值更好，则用该粒子的适应值替换全局最优值，记录全局最好位置gbest；

Step5按照式(19)、(20)对c1、c2进行线性调整，通过式(16)、式(17)更新粒子的速度和位置；

Step6判断是否满足结束条件，如若最优解精度不够或者没有达到Kmax，则返回第二步。

3 求解算例

例1该例子由2个制造商，2个零售商，2个消费者组成，如图所示：

图2 例1供应链网络结构

制造商的生产成本函数：

制造商和零售商的交易成本函数：

零售商的管理成本函数：

需求市场的需求函数：

d1(ρ3)=-2ρ31-1.5ρ32+1000d2(ρ3)=-2ρ32-1.5ρ31+1000

零售商和消费者的交易成本函数：

c11(Q2)=q11+5,c12(Q2)=q12+5c21(Q2)=q21+5,c22(Q2)=q22+5

参数设置与实验结果

图3 蜂群算法、标准粒子群算法与两种改进粒子群算法收敛图

在四种智能算法中，群体规模为200，粒子搜索空间范围为[0,400]，迭代次数为500次。蜂群算法Limit设置为50次，标准PSO算法中取定c1=c2=2，两种改进算法中c1,c2的取值范围为[0.8,2]，算法实验50次取均值。在Matlab2010a上进行实验，学习因子异步变化的粒子群算法在第367次迭代后取得最优值，蜂群算法，标准粒子群算法与两种改进算法的函数值Ψ1与迭代次数关系如图3所示。

四种算法取得的最小值与具体结果如表1所示。

表1 蜂群算法、标准粒子群与两种改进算法结果比较

例2该例子的供应链网络结构同例1，将f1(q),c11(q11),c12(q12)做如下改动：

智能算法参数设置同例1，学习因子异步变化的粒子群算法在第453次迭代后取得最小值,四种算法的函数值Ψ1与迭代次数关系如图4所示。

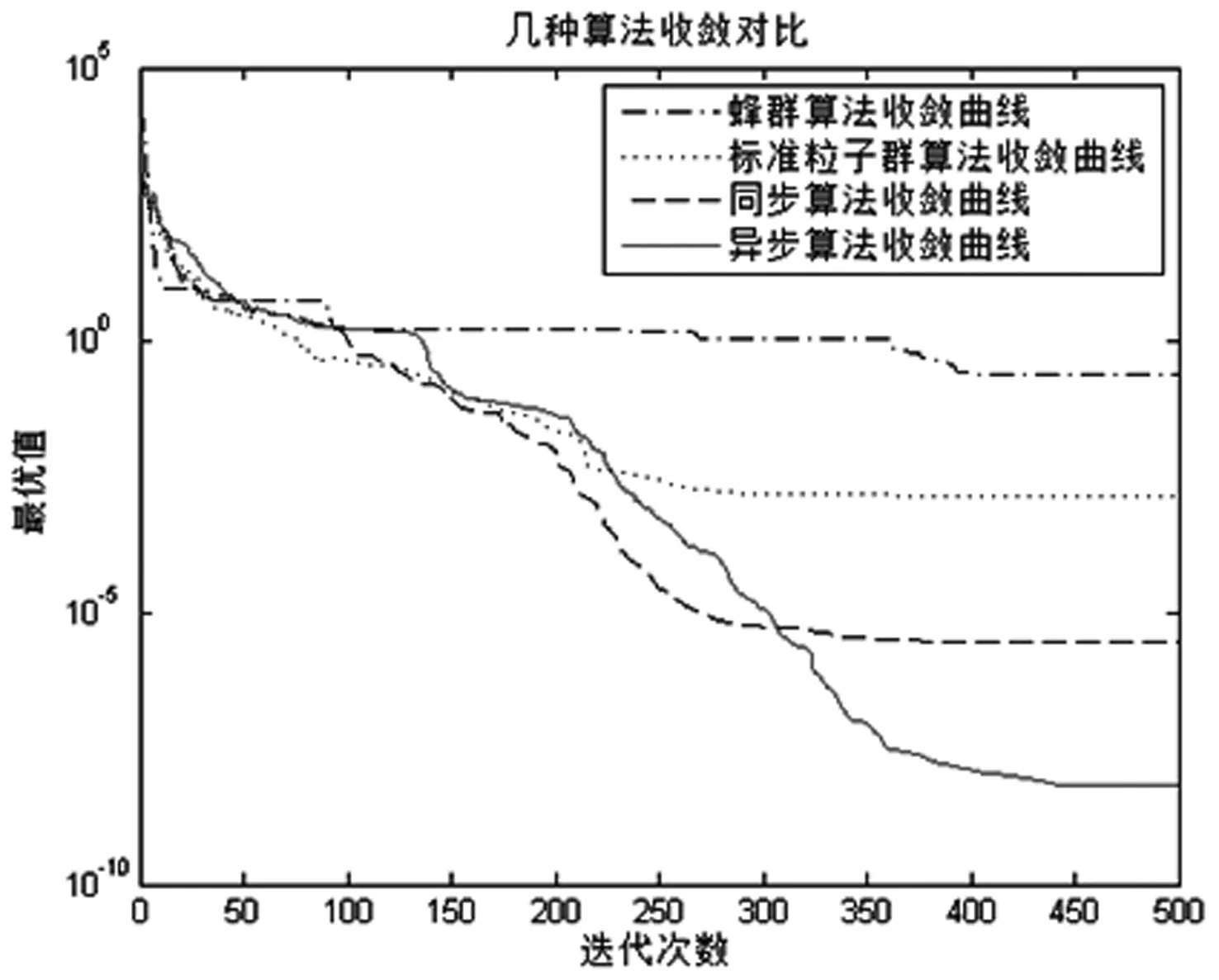
图4 蜂群算法、标准粒子群算法与两种改进粒子群算法收敛图

四种算法取得的最小值与具体结果如表2所示。

表2 蜂群算法、标准粒子群与两种改进算法结果比较

例3该算例由2个制造商，3个零售商，2个消费者组成，如图所示：

图5 例3供应链网络结构

制造商的生产成本函数：

制造商和零售商的交易成本函数:

零售商的管理成本函数：

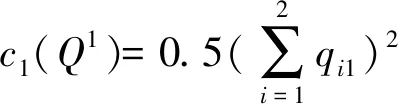
需求市场的需求函数：

d1(ρ3)=-2ρ31-1.5ρ32+1000d2(ρ3)=-2ρ32-1.5ρ31+1000

零售商和消费者的交易成本函数：

c11(Q2)=q11+5,c12(Q2)=q12+5

c21(Q2)=q21+5,c22(Q2)=q22+5

c31(Q2)=q31+5,c32(Q2)=q32+5

四种智能算法种参数设置同例1，学习因子异步变化的粒子群算法在第432次迭代后取得最小值，四种算法所得到的函数值与迭代次数关系如图6所示。

图6 蜂群算法、标准粒子群算法与两种改进粒子群算法收敛图

四种算法取得的最小值与具体结果如表3所示。

表3 蜂群算法、标准粒子群与两种改进算法结果比较

例4该算例由3个制造商，2个零售商，3个消费者组成，如图所示:

图7 例4供应链网络结构

制造商的生产成本函数：

制造商和零售商的交易成本函数：

零售商的管理成本函数：

需求市场的需求函数:

d1(ρ3)=-2ρ31-1.5ρ32+1000d2(ρ3)=-2ρ32-1.5ρ31+1000d3(ρ3)=-2ρ33-1.5ρ31+1000

零售商和消费者的交易成本函数：

c11(Q2)=q11+5,c12(Q2)=q12+5

c13(Q2)=q13+5,c21(Q2)=q21+5

c22(Q2)=q22+5,c23(Q2)=q23+5

四种智能算法种参数设置同例1，学习因子异步变化的粒子群算法在第355次迭代后取得最小值，四种算法所得到的函数值Ψ1与迭代次数关系如图8所示。

图8 蜂群算法、标准粒子群算法与两种改进粒子群算法收敛图

四种算法取得的最小值与具体结果如表4所示。

表4 蜂群算法、标准粒子群与两种改进算法结果比较

结果分析：四个例子分别给出了四种算法在求解最优值时的收敛曲线，其中纵坐标采用以10为底的对数形式。例1与例2需要求解12个变量，四种算法均能收敛。蜂群算法收敛速度最慢，并且最优解的精度也不高。标准粒子群优化算法和同步变化学习因子的算法在前期的收敛速度与精度基本一致，中后期可看出同步变化学习因子算法有较强的开采能力。异步变化学习因子从最开始就表现出较强的搜索与开采能力，最优值曲线下降迅速，能够在前期准确定位最优解的位置，后期进行深入的挖掘，最终在第367与453次迭代后找到最优解。

例3与例4的供应链网络结构相比例1与例2更复杂，需要求解17个变量，蜂群算法收敛效果并不理想，在前期就已经陷入局部最优，收敛精度也不高。标准粒子群优化和同步变化学习因子的算法相比蜂群算法收敛速度和精度都较好，但是在中期250代左右收敛速度迅速变慢，表示其陷入局部最优解，后期的开采能力也较弱。而异步变化学习因子收敛速度最快，在中期能够跳出局部最优解继续寻找全局最优解的位置。

从四个例子可以看出，学习因子异步变化的粒子群算法的最优值曲线呈近似直线的下降，其在解决供应链网络求解问题中的效果尤为突出。其中蜂群算法非常容易“早熟”，在最优解的搜索上停滞不前，结果精度不高，开采能力较差；标准粒子群算法与学习因子同步变化的粒子群算法都能够搜索到最优解附近，但是不能深入的挖掘出最优解，最终也陷入了局部最优；从四个表中也可以看出，学习因子异步变化的粒子群算法收敛的精度远高于其他算法，改进的算法在搜索前期能够在解空间内广泛的搜索不至于陷入局部最优，而在迭代的后期又能在近似最优解附近深入的探索，种群始终有较强的探索能力，说明改进的粒子群算法有效的平衡了全局搜索与局部搜素的能力。相比Nagurney的修正投影法，两种算法得到的结果基本一致，但是在求解过程中，改进的智能算法完全不会受到李氏常数、初值条件、或者迭代步长的干扰，是完全随机的在解空间进行搜索的结果。

4 结论

本文研究了供应链网络均衡问题以及求解方法，首先介绍了确定需求下的供应链网络均衡模型，提出了一种异步线性改变学习因子的粒子群算法，并对该问题进行求解。通过四个实值算例，将该方法与蜂群算法、标准粒子群算法、学习因子同步变化的粒子群算法进行比较，实验结果表明，改进的算法在求解该问题时有更好的全局和局部搜索能力，在收敛速度和精度有显著的提高，为求解供应链网络均衡问题提供了一种新的有效的方法。