基于BP算法的低空无线信道数学建模研究

2020-10-22陈俊英曾浩宇

现代电子技术 2020年20期

陈俊英　曾浩宇

摘要：为了保证低空无线信道功率谱的稳定性，提出基于BP算法的低空无线信道数学建模方法。采用BP算法获取低空无线信道的观测空间，设计信道参数提取流程，完成无线信道参数的提取。根据信道参数处理算法的具体实现步骤，采用迭代计算的方式将处理后的信道参数保存，完成低空无线信道参数处理算法的设计。通过分析低空无线信道数学模型的建立过程，实现基于BP算法的低空无线信道的数学建模。仿真实验结果表明，基于BP算法的低空无线信道数学建模方法与基于EM算法的低空无线信道数学建模方法相比，低空无线信道的功率谱更稳定，具有较好的应用效果。

关键词：低空无线信道; 数学建模; BP算法; 信道参数提取; 参数处理算法; 仿真实验

中图分类号： TN913?34 文献标识码： A 文章編号： 1004?373X（2020）20?0046?04

Research on BP algorithm based mathematical modeling of low?altitude wireless channel

CHEN Junying， ZENG Haoyu

（College of Sciences， Hebei Agricultural University， Baoding 071001， China）

Abstract： A BP algorithm based mathematical modeling method of low?altitude wireless channel is proposed to ensure the stability of power spectrum of low?altitude wireless channel. The BP algorithm is used to obtain the observation space of low?altitude wireless channel. The extraction process of channel parameters is designed to complete the extraction of wireless channel parameters. According to the specific implementation steps of the channel parameter processing algorithm， the processed channel parameters are saved by means of the iterative calculation to complete the design of the low?altitude wireless channel parameter processing algorithm. The BP algorithm based mathematical modeling of low?altitude wireless channel is realized by analyzing the process of establishing the mathematical model of low?altitude wireless channel. The simulation experiment results show that， in comparison with the EM algorithm based mathematical modeling method of low?altitude wireless channel， the power spectrum of low?altitude wireless channel of the BP algorithm based mathematical modeling method is more stable and has better application effect.

Keywords： low?altitude wireless channel; mathematical modeling; BP algorithm; channel parameter extraction; parameter processing algorithm; simulation experiment

0 引言

低空无线通信与有线通信不同，在信息交换过程中通常会采用无形的媒介，具有较高的灵活性[1]。社会的快速发展，无线通信技术越来越被人们认可和青睐，对低空无线通信技术提出了更高的要求。低空无线通信普遍采用电磁波的空间传播特性来传输信息。随着无线通信的发展，低空通信内容也变得越来越丰富[2]。空域是国家的重要资源，低空空域通常是指距离地面3 km以内的空域，在国际民航的空域分类标准中，低空空域被用于特殊用途。低空通信是指以飞行器作为终端，与地面基站建立通信连接，实现相互通信的过程。在航空通信的早期发展中，地面人员通过在地面某一位置处安装信号装置来为飞行员提供导航服务，指明空中飞行方向[3]。如今，随着航空通信网的发展，航空通信逐渐向多媒体、宽带以及大容量的方向发展，到目前为止低空有线通信已经不能满足航空通信的要求[4]。与普通航空信道相比，低空无线信道的移动范围只限于某些特定的区域，由于低空无线信道已经不仅仅局限于语音通信，还要随时提供飞行器的位置、飞行状态等信息，甚至还要具备传送图像的功能，对未来低空无线信道的信息传输在技术上提出了更高的要求。本文将BP算法应用到低空无线信道数学建模方法中，来满足低空无线信道的信息传输需求。

1 基于BP算法的低空无线信道数学建模方法

1.1 提取低空无线信道参数

在低空无线信道数学建模之前，要对低空无线信道数据进行处理，才能确保低空无线信道功率谱的稳定性。低空无线信道数据的处理核心是信道参数的提取，本文利用BP算法对低空无线信道的接收信号进行相应处理，从信号处理过程中提取每个路径的时延、多普勒频移、复振幅等参数。

低空无线信道参数的提取方法有很多，最常用的就是EM算法、最大似然估计算法，这两种算法在提取低空无线信道参数时，容易出现参数读取错误的现象[5]，因此本文采用BP算法来提取低空无线信道参数。BP算法是一种基于网络空间分解的方法，获取到低空无线信道的观测空间以后，可以将观测空间分解为噪声子空间和信道子空间[6]。

其中，组成低空无线信道子空间的特征向量与无线信道数据的协方差矩阵相对应，利用两者之间的对应关系来估计低空无线信道的方位。低空无线信道参数的提取流程如图1所示。

在低空无线信道参数的提取过程中，可以直接从数据接收机中提取出无线信道参数，将信道参数转化为Matlab数据格式，将数据库中不合理的信道参数去除，然后根据低空无线信道中的冲激响应完成信道参数的提取[7]。

1.2 设计低空无线信道参数处理算法

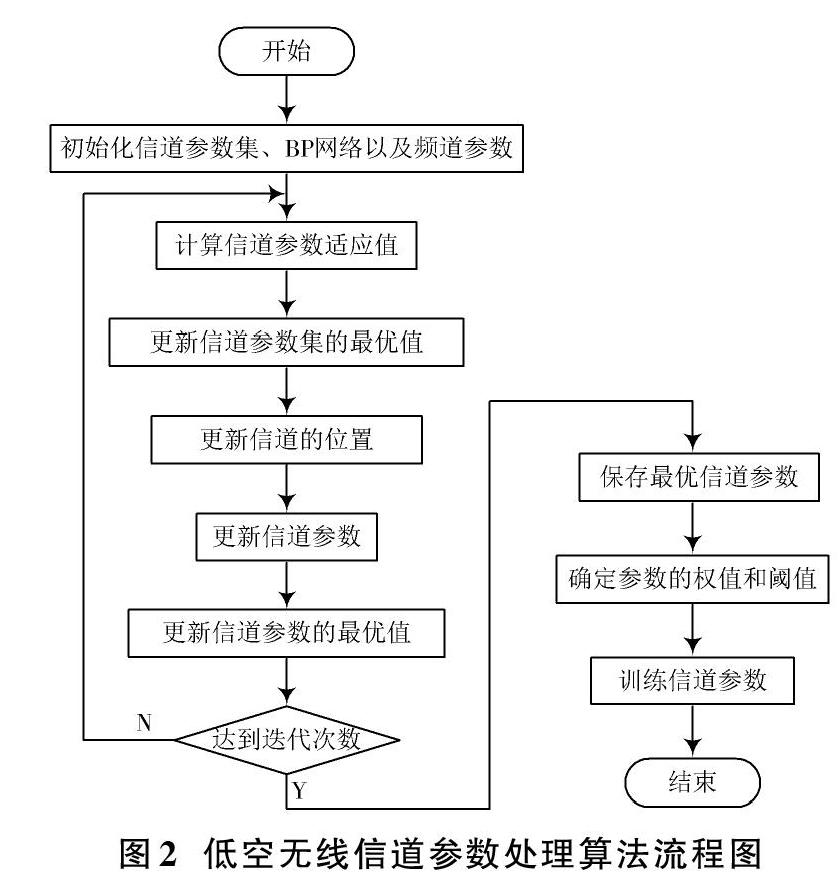
提取的低空无线信道参数由于电磁波的干扰，会掺杂噪声，将提取的参数导入到参数处理算法中，确保低空无线信道功率谱的稳定性。低空无线信道参数处理算法流程如图2所示。

根据无线信道参数处理算法流程图，可以将参数处理算法描述为：

输入：训练无线信道参数的输入和输出;

输出：训练后的BP网络。

步骤1：初始化无线信道参数。

首先初始化BP网络，确定低空无线信道参数的个数、训练次数以及训练目标;然后初始化无线信道参数集，获取参数集的规模、参数位置、大小以及参数的维数等，其中参数的维数由阈值的个数决定[8]，参数迭代次数由无线信道数量决定;最后初始化无线信道参数，包括无线信道的感知距离和拥挤度因子[9]。

步骤2：根据无线信道参数的位置初始值进行BP网络中无线信道参数的设计，包括无线信道参数的权值和阈值。

步骤3：无线信道参数的迭代。无线信道参数的适应度值是由BP算法中的网络误差决定的[10]，低空无线信道参数的适应值和全局最优适应值的确定过程为：对于第[j]代的每一个无线信道参数[i]，计算出每一个无线信道参数的适应值[pi，j]，并将适应值最小的无线信道参数记为[I]，对无线信道参数[I]进行计算，判断当前无线信道参数是否陷入低空无线通信的局部极值，如果满足条件[nf>0]，且信道参数中心位置[Xc]的适应值[Yc]满足[Ycnf>δYi]，且存在[Yc

步骤4：判断低空无线信道参数的位置是否超出了提前设定的范围。

步骤5：检查低空无线信道参数处理算法迭代的停止条件是否满足BP网络误差要求，满足要求直接转向步骤6进行信道参数处理，无线信道参数的全局最优值[pg]的每一个权值和阈值都可以作为计算结果，否则返回步骤3重新迭代。

步骤6：将步骤5计算出的权值和阈值传输给BP网络开始处理，将处理后的无线信道参数保存[11]。

由于提取低空无线信道参数过程中会受到干扰，利用参数处理算法，将无线信道参数进行初始化，利用迭代计算的方式将处理后的信道参数保存，完成低空无线信道参数处理算法的设计，进而通过无线信道数学模型建立流程，实现基于BP算法的低空无线信道数学建模。

1.3 建立低空无线信道数学模型

传统的低空无线信道数学建模方法存在复杂度高、消耗时间长的缺点，在实际应用中很难确保信号传输的安全性。

采用BP算法建立的低空无线信道数学模型，可以确保低空无线信道功率谱的稳定性。低空无线信道数学模型建立过程如下：

Step1：在提取信道参数基础上，计算接收无线信道场强，利用BP算法建立低空无线信道路损模型及无线信道参数回放模型。

Step2：利用BP算法提取参数集中多径对应的信道参数，每个参数集中的信道参数包含时延、信道幅度、到达角和离开角[12]，计算所有信道参数的变化范围。

Step3：在步骤2的基础上，将每一个信道参数按照不同的分类方式划分成不同的子组，假设第一个参数集中信道参数为[m1]，第[n]个参数集中的信道参數为[mn]，参数集中最大信道参数数量为[m]，如果[mn

Step4：将参数集分为训练样本和验证样本，将训练样本输入不同的神经网络进行训练，利用验证样本来验证模型的可用性，直到找到精确的信道数学模型[14]。

低空无线信道数学模型建立流程如图3所示。

2 仿真对比分析

2.1 仿真参数设置

为验证基于BP算法的低空无线信道数学建模方法的实际应用效果，进行仿真实验。仿真实验场景为由低空平台组成的无线通信系统，将无线发射设备安装在低空平台中，飞行器作为接收设备。仿真参数的配置如表1所示。

仿真过程中主要考虑频率为900 MHz和2.5 GHz的无线信道，由于1 800 MHz的手机用户不会轻易对2.5 GHz的无线信道产生干扰，因此将无线设备的发射频率设置为2.5 GHz。

2.2 仿真步骤

采用Matlab代码完成低空无线信道数学模型的仿真，Matlab代码的实现采用模块化的方式，仿真步骤如下：

Step1：设置仿真参数模块，在模块中事先设置好表1中的各项参数;

Step2：在主仿真模块中先调用参数模块中设置好的仿真参数，进而调用不同无线信道仿真模块，逐一生成仿真信号，将生成的仿真信号导入到统计模块，分析仿真信号的特性;

Step3：输入仿真参数，用BP算法对信号进行多径叠加，输出仿真信号;

Step4：将仿真信号导入到统计特性分析模块，分析仿真信号的时域、频域等特性;

Step5：得出实验结果。

2.3 实验结果分析

利用上述的仿真步骤，以信道频率为自变量，获取低空无线信道的功率谱情况，绘制低空无线信道功率谱稳定性对比曲线，如图4所示。

从实验结果中可以看出，随着信道频率的增加，基于BP算法的无线信道数学建模方法获取的无线信道功率谱比较稳定，功率谱的震荡范围在-20～15 dB之间，保证了低空无线信道功率谱的稳定性;而基于EM算法的无线信道数学建模方法获取的无线信道功率谱，无论频道频率如何变化，信道功率谱震荡变化始终较大，震荡区间已经接近90 dB。

3 结语

本文进行了基于BP算法的低空无线信道数学建模研究。先采用BP算法获取低空无线信道的观测空间，估计低空无线信道的方位，完成无线信道参数的提取。由于提取低空无线信道参数过程中会受到干扰，利用信道参数处理算法流程，通过将无线信道参数初始化，利用迭代计算的方式将处理后的信道参数保存，完成低空无线信道参数处理算法的设计。通过分析低空无线信道数学模型的建立过程，实现了基于BP算法的低空无线信道数学建模。仿真实验结果表明，基于BP算法的低空无线信道数学建模可以确保低空无线信道功率谱的稳定性，实际应用效果更好。

参考文献

[1] 卢艳萍，陶成，刘留，等.基于测量的大规模多天线无线信道时间色散特性分析[J].北京交通大学学报，2017，41（2）：59?66.

[2] 王晶晶，刘伟，夏宇，等.半封闭走廊中无线信道传播特性分析与建模[J].计算机工程，2019，45（7）：147?153.

[3] 李树，孙宁姚，张蕊，等.39 GHz室外微蜂窝信道测量、建模与仿真研究[J].电波科学学报，2017，32（5）：498?506.

[4] 张娣，张焱，文晋晓，等.太赫兹频段星地通信信道建模与仿真[J].电波科学学报，2017，32（5）：612?618.

[5] 卫容宇，聂敏，杨光，等.基于软件定义量子通信的自由空间量子通信信道参数自适应调整策略[J].物理学报，2019，68（14）：302?310.

[6] 耿绥燕，范宁宁，王琦，等.28 GHz MIMO无线信道特性分析与研究[J].电波科学学报，2017，32（5）：520?528.

[7] 崔壮壮，钟章队，官科，等.基于射线跟踪的车联网毫米波信道准平稳区间研究[J].电波科学学报，2017，32（5）：570?577.

[8] 周忠眉，李莎莎.一种改进的基于规则实例多覆盖分类算法[J].数据采集与处理，2017，32（6）：1232?1238.

[9] 葛朋，杨波，毛文彪，等.基于引导滤波的高动态红外图像增强处理算法[J].红外技术，2017，39（12）：1092?1097.

[10] 黄增树，孙进平，谭维贤，等.弧形阵列3D?SAR成像處理算法研究[J].信号处理，2019，35（4）：523?530.

[11] 李波，郝杰，李开放，等.采用波导技术的地下传感网通信信道建模[J].西安科技大学学报，2018，38（6）：1036?1040.