核心素养下整体关联教学的应用举例
2020-10-21张波
张波

摘 要:以“多边形”和“平方差公式”为例,分别从“框架式”和“文化源”两个角度进行整体关联教学,利用数学知识关联和数学史文化关联,经历知识的发生发展过程,感悟数学知识的整体性,培养学生思维,发展学生核心素养。
关键词:关联;四边形;平方差公式
《全日制义务教育数学课程标准(实验稿)》指出“应注重学科内容选择、活动设计的有机联系”[1],强调课堂教学的整体性设计;比利时教育家德克乐利在19世纪末就提出教学遵循“整体化”和“兴趣中心”的原则;章建跃教授在《数学教育之取势明道优术》中指出“在面对一个新的数学研究对象是,要有“整体观”,要先为学生构建研究的整体框架”[2]。開展整体关联教学有利于数学教师在实践的过程中更好地理解数学学科核心素养的本质,将数学学科教学和人才培养有机融合,促进教学相长;对学生而言,整体关联教学有利于学生在学习数学过程中较好地构建学科知识体系,真正把握学科本质,最终整体达成涵养数学学科核心素养的目标。
一.以“多边形”为例的“框架式”整体关联教学
思考 学生在八年级上册已经对三角形有了比较深刻而且完整的认识,所以考虑立足三角形相关知识,找到相通,通过与三角形的整体关联,找到多边形与三角形相同的本质,在类比中把多边形同化,建立类似知识系统之间的整体关联,实现知识的正迁移,实现思维的提升,进而提升学生核心素养。
片段1.概念关联
出示图片,抽象出三角形,回顾三角形定义;出示图片,抽象出四边形,类比三角形定义得出四边形定义;进而关联归纳出多边形的定义。以此类推,学生自主探究,类比三角形的内角、顶点、边等概念关联得到出四边形和多变形的相关概念。
教师:从这张图片中我们能抽象出什么图形?(出示图片)
众生:三角形。
教师:三角形是我们已研究过的图形,它是如何定义的呢?
学生1:由不在同一直线上的三条线段首尾顺次相接形成的图形。
教师:从这张图片中我们又能抽象出什么图形呢?(出示图片)
学生2:四边形。
教师:对,是四边形,那么谁能给它下个定义呢?
学生3:由不在同一直线上的四条线段首尾顺次相接形成的图形。
教师:很好,请问你是怎么得到的呢?
学生3:我是模仿三角形的定义。
教师:对,我们可以类比三角形的定义快速得出四边形的定义。那么同学们能类比三角形和四边形的定义归纳出多边形的定义吗?
学生4:由不在同一条直线上的若干条线段首尾顺次相接形成的图形。
教师:类比得很好,我们说,在同一平面内,由任意两条都不在同一条直线上的若干条线段(线段的条数不小于3)首尾顺次相接形成的图形叫做多边形。接下来请同学们根据刚才的方法,类比三角形的内角、外角、顶点、边等相关概念,自主探究四边形的相关概念,进而归纳出多边形的相关概念。
(学生合作交流,教师引导,完成表格。始终沿着类比三角形概念得出四边形概念进行关联探究,进而由特殊到一般,归纳出多边形概念这一条线贯穿这一环节)
设计分析:奥苏贝尔指出:影响学习的最重要的原因是学生已经知道了什么,我们应当根据学生原有的知识状况进行教学。学生在八年级上册已经对三角形有了深刻而完整的认识,了解了三角形的相关概念,本环节中,教师引导学生类比三角形定义得出四边形和多边形定义,让学生体会在之前学习过程中积累下的三角形相关知识及经验可以适当迁移,推广到四边形学习中来,进而学生以此类推,四边形的内角、外角、顶点、边等相关概念的生成自然而然,使得四边形的新知识可以很快生长出来。
片段2.性质关联
教师:回顾三角形的探究经历,三角形概念后我们探究的是三角形的性质,最先了解的是三角形内角和定理,那么同学们知道吗?
学生5:三角形内角和等于180°。
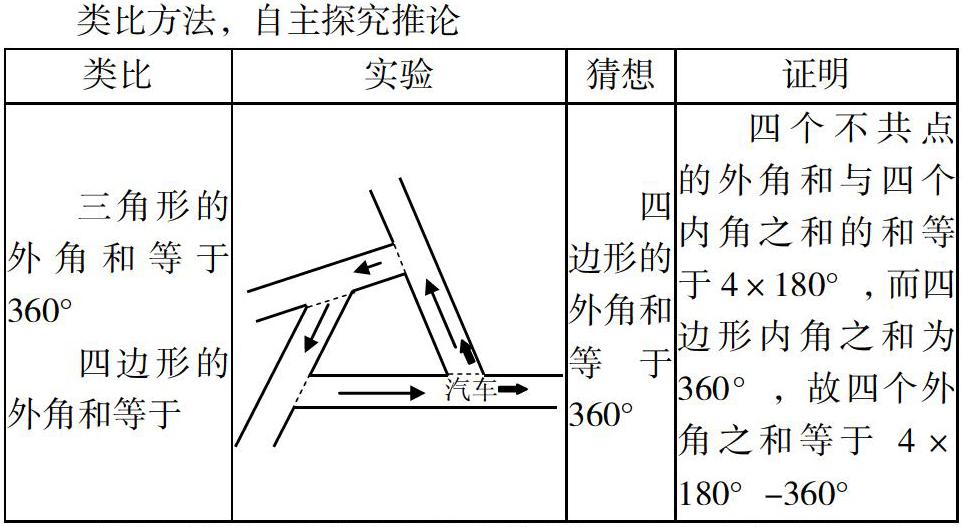
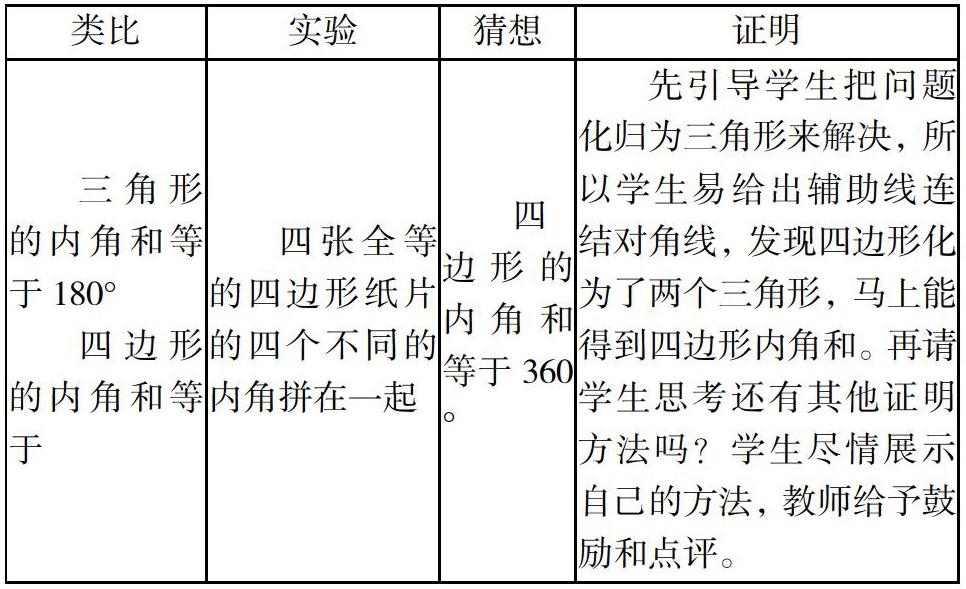
教师:那么四边形的内角和等于多少呢?让我们用我们手上的道具,跟着这张表格一起来探究吧。
(学生根据已有关联经验继续小组交流,合作完成表格。表格中的实验环节有一定的难度,教师事先给每个小组准备好道具,学生自己创设情境,动手操作。)
设计分析:《标准》指出:“学生学习应当是一个生动活泼的、主动的和富有个性的过程。认真听讲、积极思考、动手实践、自主探索、合作交流等,都是学习数学的重要方式。学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程。”本环节,通过类比,提出疑问,带着疑问进行实验,根据实验大胆猜想,进而证明,用类比—实验—猜想—证明的方法师生共同探究四边形内角和定理,再根据这样的方法,学生动手实践、合作交流,自主探究四边形定理的推论。类比—实验—猜想—证明这一数学体验让学生置身数学活动中,亲历具体的操作过程,感受数学对象,发现数学问题,领悟思想方法,获取活动经验,能有效提升学生的数学核心素养。
二.以“平方差公式”为例的“文化源”整体关联教学
思考 上述课例是通过知识内在逻辑关系建立的体系,教师在关注知识的逻辑顺序的同时,应与学生的心理发生顺序一致,探究知识究竟为何会产生,追溯知识的发生和发展历史。关于平方差公式最早可追溯到古巴比伦数学泥版,记载了大量的二元二次方程组问题,当时解决的方法是“和差术”,公元3世纪,古希腊数学家丢番图也利用和差术来解二元二次方程(如:已知两数的和为20,乘积为96,求这两个数)。在中国古代数学中,赵爽在注解《周髀算经》时,给出了平方差公式的几何证明。后来的希腊数学中,平方差公式和等周问题密切相关,芝诺多鲁斯著《论等周图形》一书,证明了如下命题:“在边数相同的等周多边形中,等边且等角的多边形面积最大。”[3]
片段1.现实中的等周问题,引出课例
