谈《直线与平面平行》复习课项目驱动法提升数学核心素养

王英君

在高中数学课堂上，为了进一步让学生在问题驱动下有效开展课堂学习，教师首先要激发学生对于问题的探究欲望，只有这样，学生才会积极参与到课堂教学过程中来。教师可以通过结合教学内容，巧设问题情境的方式进行教学，有效激发学生对数学学习的好奇心。在这个过程中，再结合教材给予学生适当引导，让学生沿着自己的思路进行探究，并鼓励学生针对数学知识点更清晰地提出自己的困惑，将其问题意识充分激发出来，进而巩固自身所学知识，提升数学核心素养。

笔者在高三复习《直线与平面平行》这一节课时，为了让学生理解并证明直线与平面平行，也为了进一步激发学生这一节课的探究学习欲望，在教学过程中，首先进行课标分析，以立体几何的有关定义、公理和定理出发，认识和理解空间中线面平行、面面平行的有关性质与判定定理，并能够证明相关性质定理。能运用线面平行、面面平行的判定及性质定理证明一些空间图形的平行关系的简单命题。培养学生核心素养，锻炼学生的直观想象能力，培养学生的逻辑推理能力。然后确定教学目标，知识与技能。理解并掌握直线与平面平行的判定定理，平面与平面平行的判定定理。学会利用线线平行及面面平行，证明线面平行的过程与方法。通过对平行问题的分析，解答培养学生的直观感知能力，逻辑推理能力，使学生体会数学探索活动。培养学生直观到理性的思维方法，情感态度与价值观。培养学生认真严谨的学习态度。培养问题意识，孕育创新精神。

第一阶段，提出项目。采用项目驱动教学法，项目的提出是教学内容的开始。让学生分组协作，如此一来，便可调动学生的积极态度。

近五年高考全国卷考查情况如下。

2019年全国卷 第19题（1）问（4分）（线面平行的证明）

2018年全国卷III第19题（2）问（6分）（线面平行的探索）

2018年全国卷II第9题（5分）（异面直线成角）

2017年全国卷II第18题（1）问（4分）（线面平行的证明）

2016年全国卷III第18题（1）问（4分）（线面平行的证明）

2015年全国卷II第19题（1）问（6分）（利用面面平行探索交线）

热点预测，2020年主要考查平行的判定与性质，其中线线平行、线面平行、面面平行的相互转化是高考的热点。以选择题、填空题或解答题的一问呈现，分值为5-6分常常以柱体或椎体为载体，考查推理论证能力和空间想象能力，关于平行中的存在性问题也应引起重视。

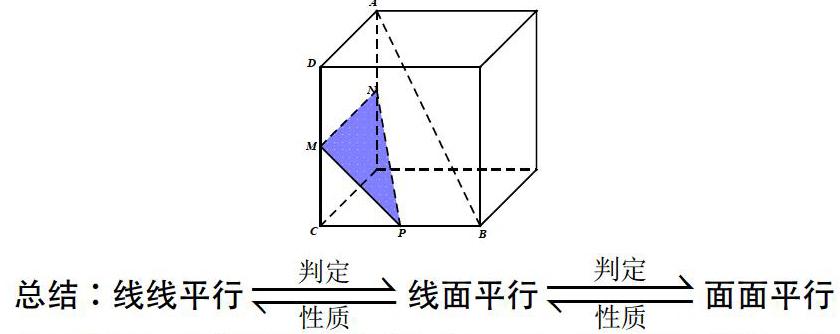
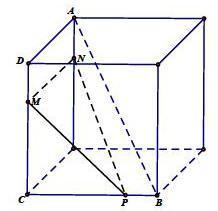
例题，如图所示，在正方体中，A，B为正方体的两个顶点，M，N，P为其所在棱的中点，求证： 平面

总结：线线平行 线面平行 面面平行

第二阶段，组织学生来完成任务。正如前面所提到的，以分组的形式将班级学生分成若干个项目小组。在这一环节，旨在培养学生的自主性以及独立解决问题的能力，活跃学生的数学思维。对此，老师需要充分发挥出组织、协调的作用。不要过多干扰学生，当然，可以给予学生一定的帮助，引导学生如何在已有的知识中分析出新的观点。

变式1：当 分别是靠近 的三等分点时，求证： 平面

变式2：当 是中点， 是靠近 的四等分点时，在线段 上是否存在点 ，使得 平面 ？

引导学生由直观感知往理性分析的角度转变。要想证明线面平行，需要证明线线平行，怎样找直线是关键。

我们知道，线面平行的性质定理即可得线线平行，那么经过直线 的平面与平面 的交线一定与 平行，也就是说由结论出发，去找结论成立的条件。

通过面面平行证线面平行，需构造与平面 平行的平面，根据面面平行的判定定理，两平面平行，需要线面平行。从根本上说需要线线平行，只需再找一条平行于平面 且与直线 共面的直线即可，这样构造的平面一定符合要求

设计意图让学生对线面平行在高考中的考查方式、考查内容有清晰的认识，以便查缺补漏，完善知识网络。让学生明确线面平行中，这条直线只与平面中的某一类直线平行。提醒学生在做证明题时，定理所需条件缺一不可，必须写全，否则证明不成立。大多数同学都是通过直观感知来确定辅助线的做法，虽然证明了这个问题，但是比较盲目，缺乏理性分析，遇到更一般的问题时，很有可能不能顺利完成。变式题的设计想法是打破特殊情形，让问题更具有一般性，引导学生做进一步地思考.

第三阶段，评估评价。所谓知识，就是对知识的掌握情况，在评价上要依据学生课堂提问与回答情况，以及各項目小组组内、课堂上的讨论发言情况。所谓技能，是指实践应用能力，生成新的问题（变式）在问题情境创设之后，教师还要借助相应的教学方法来让学生深入探究，进一步发挥问题驱动教学法的教学效果。学生经过充分的问题探讨，才能够逐渐养成问题意识，强化数学思维。具体而言，当问题提出之后，教师要鼓励学生以小组的形式参与到讨论中来，给予每位学生发表自己观点的机会。并鼓励学生在探究中善于并积极提出问题，启发学生多角度看待问题，培养学生“善问”的意识，进一步强化学生的数学思维。

在教学过程中通过直观感知、操作确认，归纳概括出判定定理。引导学生懂得将立体问题平面化、线面问题线线化。在授课中培养了学生数学核心素养中的数学抽象、逻辑推理、直观想象等能力。

综上所述，将项目教学方法引入到高中数学课堂实践教学中，对于数学教师而言，可以进一步明确教学目的。整个实践项目的设计，均围绕着这一教学目标来展开，最大限度地体现出教学内容。对于学生来说，很好地提高了学习的主动性，从本源上解决了传统教学模式下“教师一直讲，学生一直听”的灌输式沉闷的课堂氛围，促使学生摆脱对老师的依赖性，增强了独立思考问题、解决问题的创新思维能力，进而提升自身的综合数学素养。

参考文献：

[1]周洪新 《数学大世界·下旬刊》2019年第02期《基于问题驱动的高中数学课堂教学》

[2]刘建富 《教学管理与教育研究》2017年第09期《高中数学教学中的项目教学模式应用》