重型载货汽车柔性车架的轻量化研究

李韶华，张 兵，冯桂珍

（1．石家庄铁道大学械工程学院，河北 石家庄 050043；2．河北省交通安全与控制重点实验室，河北 石家庄 050043）

1 引言

随着重型载货汽车在交通运输行业里应用越来越广泛，节能环保问题成为汽车行业的重中之重，汽车结构轻量化在提高汽车动力性的基础上可以有效的降低汽车的燃油消耗[1]。重型载货汽车长期行驶在较为复杂多变的工况，甚至普遍存在着严重的超载现象，车架不但需要承载整车及货物的重量，还要承受来自各种路况的激励，车架的柔性表现的非常明显[2-4]。另外，车架自身的重量在整车当中占有很大成分，约占10%，并且绝大部分油耗和自身重量有关，根据文献[5]可知重量降低10%，油耗和排放分别可下降7%、4%，因此有必要对车架进行轻量化研究。减轻车架质量有三种方法，一种是采用高强度的轻质材料，一种是对汽车零部件进行优化，最后一种是采用新型制造技术[6]。对于汽车构件的研究从最初的传统经验法演变成有限元方法进行设计，在达到轻量化目的的同时也缩短了开发周期[7-8]。因此，文章基于有限元软件Ansys 建立车架的柔性模型，利用多目标遗传算法计算得到车架厚度的最优解，对车架进行轻量化设计，并对优化后的车架进行静力分析、模态分析以及疲劳寿命预测，通过与优化前的车架进行对比验证轻量化的效果。

2 车架参数化建模

以某重型三轴载货汽车为研究对象，采用Solidworks 建立了其车架三维CAD 模型，如图1（a）所示。该车架是由两根纵梁和11 根横梁组成，车架长为11.398m，宽为0.86m，高为0.302m，材料为16Mn 钢。将各部件中对力学性能影响较大的部分定义为可变参数，并在各部件特征名称前面加入Ansys-Workbench 可识别的前缀“DS_”，可实现对各纵梁、横梁部件的力学分析。为了防止车架上的一些次要零部件和工艺圆孔对车架的静力学分析产生影响，对车架进行了结构设计上的简化处理。将车架CAD 模型导入Ansys 中，并赋予车架材料属性，采用8 节点的solid45 三维实体单元进行网格划分，从而生成车架有限元模型，如图1（b）所示。车架所采用的材料为Q345 钢，材料参数，如表1 所示。

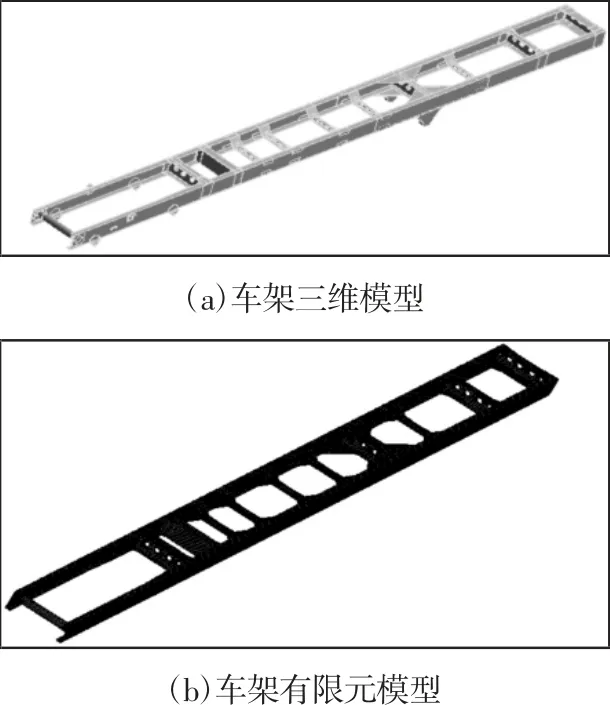
图1 重型汽车车架模型Fig.1 Heavy Truck Frame Model

表1 车架材料属性Tab.1 Material Properties of Frame

3 刚柔耦合整车模型的建立及验证

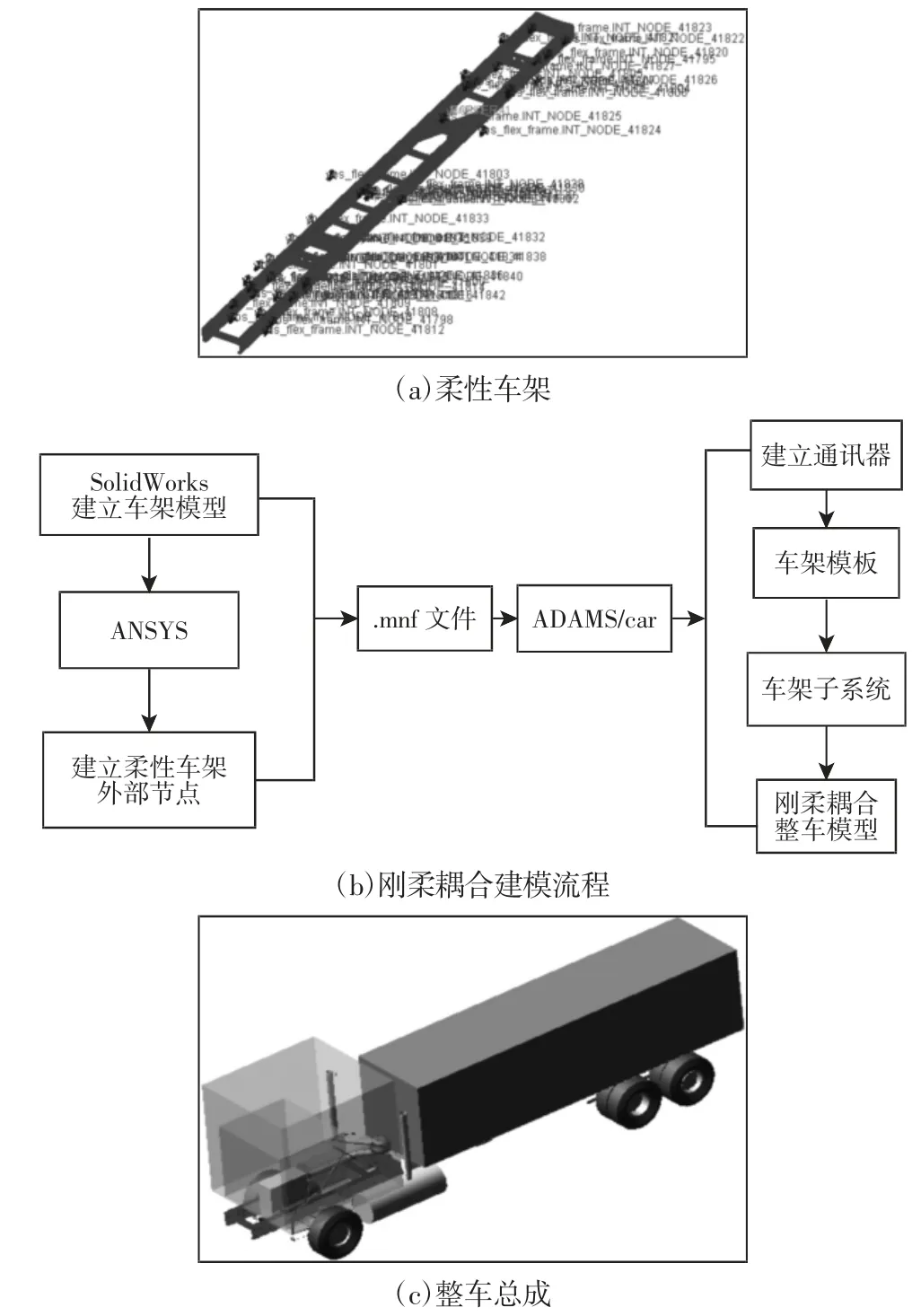
图2 刚柔耦合整车建模Fig.2 Rigid Flexible Coupling Vehicle Modeling

以往对构件的仿真分析大都采用刚性构件，当受到作用力的时候不会发生变形，在现实中由于各零件的弹性变形对于机构各部分的动态特性影响不大，大部分构件可以当作刚性体来处理，但如果考虑构件变形对结果的影响以及构件应力大小、分布和载荷输出，需要将构件当作柔性体对待，既能保证模型的准确性、还原实际工况，又能使计算结果更加准确，更好的反映各个零部件之间的连接和受力关系。因此，通过ANSYS 对车架进行有限元分析，建立车架关键点及刚性区域，最终生成.mnf 文件，导入到ADAMS/car 中，在模板界面建立车架与其他子系统相关联的通讯器，生成柔性车架，最后生成车架子系统建立了刚柔耦合重型汽车整车模型，生成的柔性车架、建模流程及整车模型，如图2 所示。且该模型的正确性已在文献[4]中得到验证。

4 车架轻量化

将Solidworks 建立的车架参数化模型导入到Ansys-Workbench 软件中，建立输入输出变量，利用优化模块Design Explore中的响应面对车架各梁进行分析，选择车架的两根纵梁和主要横梁及横梁连接件的厚度作为输入变量，总共14 个设计变量。设定好输入变量和优化条件后，对其进行迭代计算，得出各设计点的优化结果。选取车架质量最小为目标函数，车架最大应力345MPa为约束条件，利用多目标遗传算法得出14 个设计变量厚度的最优解，多目标遗传算法是目前常用的目标驱动式优化方法，实质为通过不断计算寻找符合所有约束的一个解集[9]，数学模型。如式（1）、式（2）所示。优化结果，如表2 所示。

且至少存在一个严格不等式，则称X* 为多目标优化的最优解。

式中：min f（x）—极小化的目标函数；gi（x）=0—等式约束条件；hj（X）—不等式约束条件。

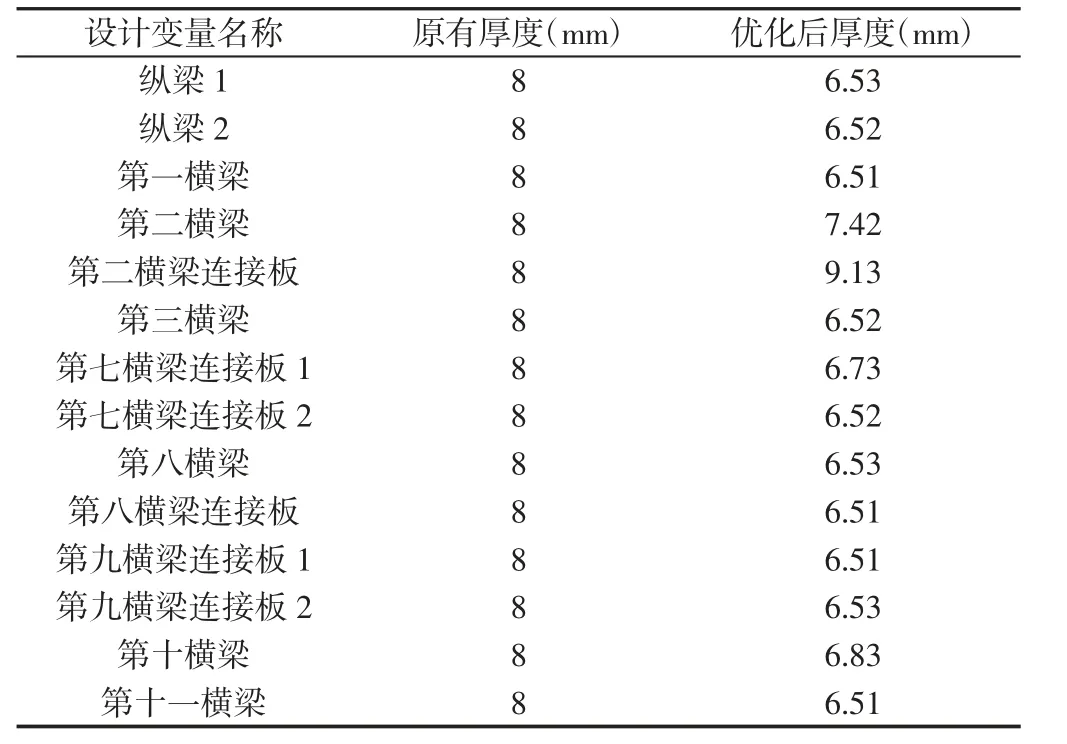
表2 车架优化前后各设计变量的厚度变化Tab.2 Change of the Thickness of Each Design Variable Before and After the Optimization of the Frame

从表2 可以看出，车架的各纵梁、横梁以及连接件厚度都相应的发生了改变，除了第二横梁连接板厚度增加外，其他梁和连接件的厚度都不同程度的进行了缩减，而车架的总质量也由原来的1278.4kg 降低到了1185.6kg，减少了92.8kg，降低了车架7.3%的质量，满足了车架轻量化的目的。

5 车架优化后静动态特性分析

5.1 车架优化后的静力学分析

为了验证轻量化后的车架能够满足正常使用要求，需要对优化后的车架进行静力学和模态分析。静力学分析选用满载弯曲、满载扭转和满载弯扭三种典型工况，将优化后的静力分析结果与优化之前的结果进行对比，并校核车架的强度。

优化后车架在满载弯曲、满载扭转和满载弯扭工况下的应力和位移云图，如图3～图8 所示。优化前后的结果对比，如表3所示。

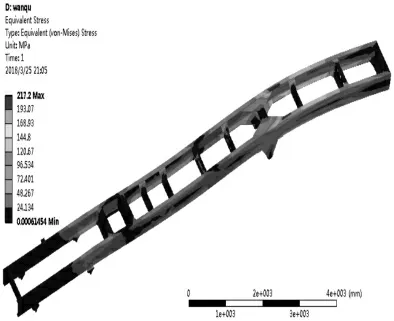
图3 满载弯曲工况车架应力云图Fig.3 Frame Stress Cloud Diagram with Full Load Bending Condition

图4 满载弯曲工况车架位移云图Fig.4 Frame Displacement Cloud Diagramwith Full Load Bending Condition

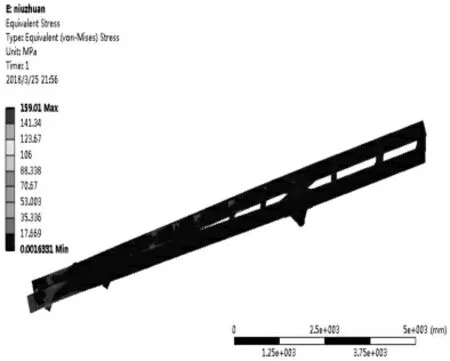
图5 满载扭转工况车架应力云图Fig.5 Frame Stress Cloud Diagram with Full Load and Torsion

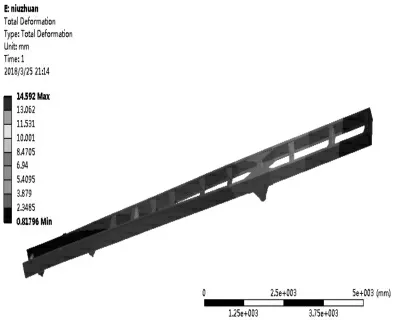
图6 满载扭转工况车架位移云图Fig.6 Frame Displacement Cloud Diagramwith Full Load and Torsion

图7 满载弯扭工况车架应力云图Fig.7 Stress Cloud Diagram of Frame Under Full Load Bending and Torsion Conditions

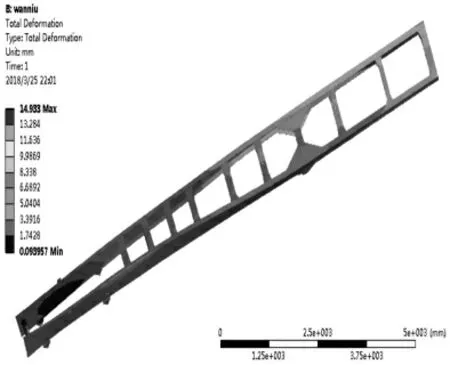
图8 满载弯扭工况车架位移云图Fig.8 Displacement Cloud Diagram of Frame Under Full Load Bending and Torsion Conditions

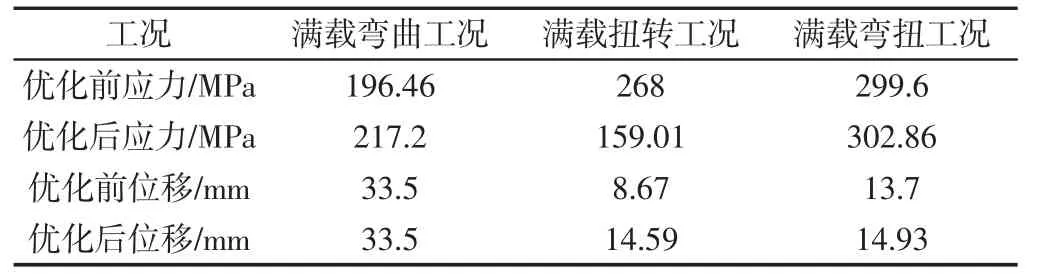
表3 车架优化前后静力分析各参数对比Tab.3 Comparison of the Parameters of Static Analysis Before and After the Optimization of Frame

从表3 和图3～图8 中可以看出，（1）车架优化后，除了满载扭转工况下的应力减小了之外，其它几个工况的应力和位移均增加。（2）在满载扭转工况下，车架的最大位移变形从优化前的左前车轮处转换到了车架的最后一根横梁和纵梁连接处的尾端，这是由于在优化过程中，车架尾端的几根横梁和左纵梁的厚度都相应的减小，而车架的中部和中后部的横梁并未进行优化，车架本身尾端较长，车架左前轮发生了翘曲，致使车架后端产生了应力集中，位移较大。（3）其它工况下的应力和位移最大部位与优化前的车架位置几乎一致。虽然大部分工况下的车架最大应力较优化之前的车架最大应力呈现增加的趋势，但均未超过车架本身材料属性的最大屈服极限，因此车架在满足轻量化的同时，其自身的强度和刚度也满足车架的正常使用要求。

5.2 车架优化后的模态分析

重型载货汽车在行驶过程中车架会受到外部激励，一个是路面不平度对车轮的激励，一个是整车发动机在运行中活塞往复运动产生的激励。一般高速公路的路面激振频率为（1～3）Hz，而发动机的激振频率可通过下式进行计算[10]：

式中：f—发动机激振频率，单位Hz；n—发动机转速，单位r/min；M—发动机的气缸数目；τ—发动机的冲程数。这里研究的三轴重型载货汽车匹配的发动机为康明斯六缸四冲程柴油发动机，发动机在怠速情况下的转速为600r/min，因此计算得到该发动机的激振频率为30Hz。分析得到优化后车架前十阶固有频率和振型，如表4 所示。

表4 车架优化前后的自由模态分析结果Tab.4 The Result of Free Modal Analysis Before and After the Frame Optimization

从表4 中可以看出，优化后的车架第二阶频率至第八阶频率均大于优化前车架的固有频率。并且优化后车架的一阶频率和二阶频率远远大于路面激振频率，不会与路面激振频率产生共振现象。但是车架的一阶扭转和车架的一阶侧向弯曲的频率非常接近，分别是20.025Hz，21.352Hz，虽然在一定程度上避免了路面激励引起的振动，但是这两个频率值只差了1.3Hz，很有可能会发生车架在低阶时的扭转弯曲耦合振动。从发动机怠速状态下的激振频率30Hz 来看，优化后的车架任何一阶频率都避开了30Hz，并且有一定差距，说明优化后的车架有良好的振动特性，在正常使用要求下不会与发动机的激振频率产生共振现象，符合实际使用。

6 车架优化后的疲劳寿命分析

重型载货汽车在行驶过程中，车架常见的工况是满载弯曲工况，因此对优化后的车架进行满载弯曲工况下的疲劳寿命预估具有实际意义。采用刚柔耦合整车分析方法，能够动态分析各种工况中柔性体的应力应变，可以为疲劳寿命分析提供更加准确的载荷数据[11-12]。利用刚柔耦合整车模型，在ADAMS/car 中以70km/h车速在随机路面下进行动力学仿真，得到车架边界载荷谱。基于nCode Design-Life 软件对车架进行满载弯曲工况疲劳寿命预估，计算流程，如图9 所示，得到优化前后车架在满载弯曲工况下的疲劳寿命云图和损伤云图，如图10～图13 所示。根据2017 年新实行的《机动车强制报废标准规定》第七条，国家对达到一定行驶里程的机动车引导报废第八小条明确指出重型载货汽车（包括半挂牵引车和全挂牵引车）行驶里程为70 万千米，结合文章研究车速为70km/h，疲劳分析输入的载荷谱时长为20s，计算得出该车架的疲劳循环次数为1.8E+006。（1）从图10～图11 中可以看出，优化前的车架最低节点的循环次数为2.05E+006，按照该节点最低循环次数疲劳寿命计算得出该车架的续航里程为79.72 万千米。（2）从图12～图13 中可以看出，优化后的车架最低节点的循环次数为1.971E+006，按照该节点最低循环次数疲劳寿命计算得出该车架的续航里程为76.65 万公里，相比优化之前的车架缩减了3.9%，仍然满足重型载货汽车行驶里程70 万公里的标准。优化后车架的中后桥第八根横梁与纵梁的连接处疲劳损伤最大，相应的其横梁和纵梁连接处也有不同程度的疲劳累积损伤，与优化前车架疲劳寿命最薄弱位置基本一致。因此，优化后的车架仍然具有很好的抗疲劳特性和可靠性。

图9 车架疲劳寿命计算流程图Fig.9 Flow Chart of Fatigue Life of Frame

图10 车架优化前疲劳寿命云图Fig.10 Fatigue Life Cloud Diagram Before Optimizationof Frame

图11 车架优化前损伤云图Fig.11 Damage Cloud Diagram Before Optimization of Frame

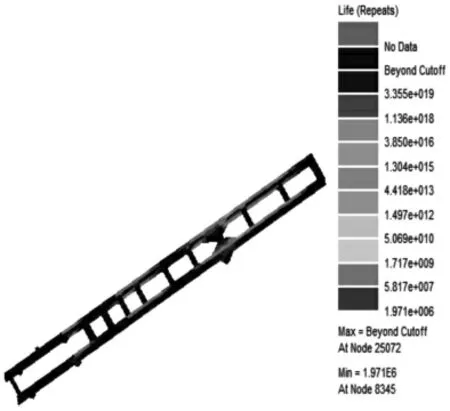
图12 车架优化后疲劳寿命云图Fig.12 Fatigue Life Cloud Diagram after Optimizationof Frame

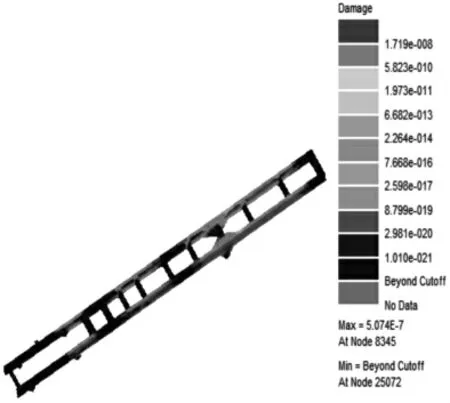
图13 车架优化后损伤云图Fig.13 Damage Cloud Diagram after Optimizationof Frame

7 结论

基于SolidWorks 对车架在不改变尺寸的情况下进行参数化建模，设置参数变量，对车架进行有限元分析，利用ANSYS 软件生成车架的.mnf 文件，然后导入ADAMS/car 生成柔性车架，建立车架与各子系统相关联的通讯器，组装成刚柔耦合重型汽车整车模型。利用尺寸优化方法对车架进行轻量化设计。对整车进行动力学仿真，得到用于分析车架疲劳寿命的边界载荷谱。对优化后的车架做静力分析、模态分析和疲劳寿命预测，并与优化前的结果进行了对比分析。研究表明，车架优化后其质量减轻了7.3%，其强度和固有频率呈现增加的趋势，其疲劳寿命降低3.9%，但仍可满足车架的正常使用要求。因此，车架优化后，既可以达到轻量化的目的，又可以保证其具有足够的强度、安全性和抗疲劳特性。