混联式混合动力汽车工况预测能量管理研究

杨亚联，石小峰

（重庆大学汽车工程学院，重庆400044）

1 引言

混合动力汽车的能量管理是发挥其构型特点的重要技术之一，目前被广泛采用的是基于规则和基于优化方法的能量管理策略。基于规则的能量管理，大多基于工程师的经验来制定规则，简单且计算快速，但工况适应性不强，并不是最优的控制方法。基于优化的能量管理主要是动态规划算法和最小值原理（Pontryagin’s minimum principle，PMP），两种算法均能获得全局最优解，但必须已知工况，而且计算量较大，缺乏实用性。基于对实时性的要求，便有了瞬时优化的能量管理，较为典型的便是模型预测算法。模型预测能量管理将优化算法应用于预测时域，通过滚动优化，不断更新预测状态量并获取最优的控制变量[1-2]。

文献[3]考虑瞬态时的油耗，应用模型预测算法，根据驾驶意图对转矩的分配做预测控制，得出了比PID 控制更好的燃油经济性。文献[4]采用随机预测模型控制算法对驾驶员需求扭矩进行预测，研究了其转矩分配问题，并建立了马尔可夫预测模型，利用动态规划作为其优化算法，燃油经济性得到显著提升。文献[5]提出了非线性和线性时变的模型预测算法，利用PSAT 软件结果与之对比实现了燃油经济性的提高，且非线性的方法提升尤为显著。

虽然上述论文对混合动力能量管理策略的工况适应性、实时性进行了针对性的研究，但是工况预测的精度还有待进一步提高。

通过应用多阶马尔可夫与神经网络作为预测模型，采用动态规划做滚动优化，建立了混联式混合动力汽车的模型预测能量管理策略，并验证了所提出的能量管理策略在工况预测精度方面的优势。

2 动力系统建模

能量管理策略是基于混合动力整车运行机理进行建立的，故需先对混合动力整车进行建模。

混联式混合动力汽车系统结构，如图1 所示。其动力系统由发动机和两个电机通过双排行星齿轮系统耦合而成，发动机和输出端转速解耦，这样发动机和电机就有了均工作在最优效率区间的可能性；在整车行驶过程中，能量管理策略根据外界行驶工况以及整车部件（空调、电池充放电等）需求，合理分配发动机、电机功率，使混合动力汽车的能量消耗最低[6]。

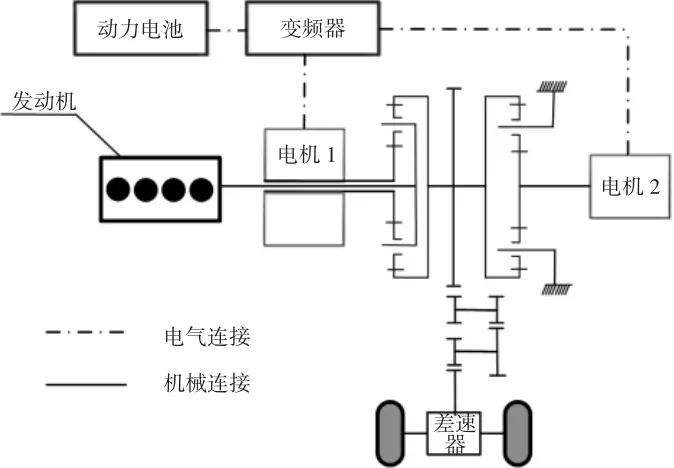
图1 混联式混合动力汽车结构图Fig.1 The Structure of Series-Parallel HEV

2.1 发动机模型

发动机的油耗计算公式为：

式中：Pe—发动机的输出功率（W）；Q—单位时间内的燃油消耗量（mL/s）；b—燃油消耗率［g/（kW·h）］；ρ—燃油的密度（kg/L）。发动机万有特性图，如图2 所示。

图2 发动机万有特性图Fig.2 Universal Performance Test Map of ICE

2.2 电机模型

两个电机均可作为电动机或发电机，电机分别是驱动电机和发电机时，计算公式为：

式中：Tm—电机的输入或输出转矩；Nm—电机的转速；ηm—电机的驱动效率；ηg—电机的发电效率。电机MG1 和电机MG2 的效率特性图，如图3 所示。

图3 电机效率图Fig.3 Efficiency Diagrams of Motor/Generator

2.3 电池模型

电池的充放电功率是两个电机的功率和，为电机提供电能并回收反馈能量，其相关公式为：

式中：Pbat—电池的充放电功率；—MG1、MG2 的效率；—两个电机的功率转换器的效率，电机驱动和发电时；k—-1 和1；Ubat—电池路端电压；Ibat—回路电流；Ebat—电池电动势；Qini—电池初始电量；Qbat—电池总容量（Ah）。电池的等效模型、内阻模型和电动势模型，如图4 所示。

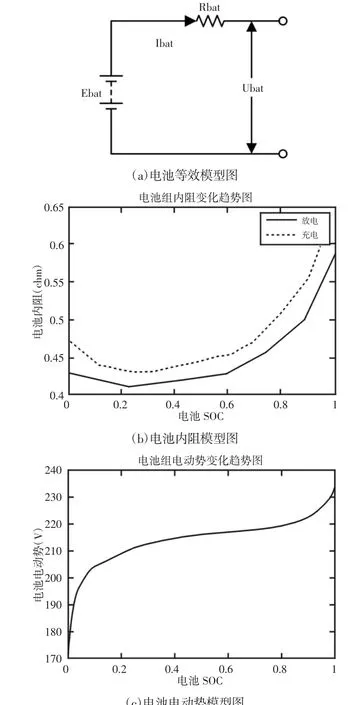
图4 电池参数模型图Fig.4 Parameter Models Diagrams of Battery

2.4 行星齿轮模型

行星齿轮机构的动力学方程为：

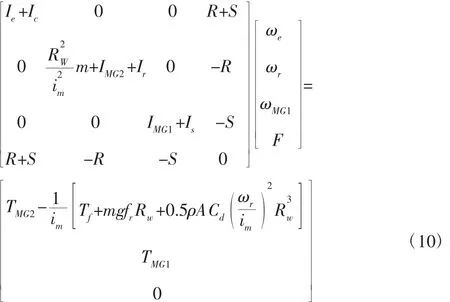
式中：T、ω、I—转矩、转速和惯量；下标r、s、p、c 和e—齿圈、太阳轮、行星轮、行星架和发动机；Cd—空气阻力系数；fr—滚动阻力系数；im—主减速比；m—整车质量；RW—车轮半径；Tf—液压制动转矩。

2.5 车辆模型

汽车行驶的动力学公式为：

式中：m—汽车整车质量；g—重力加速度；f—滚动阻力系数；α—坡道坡度；δ—汽车旋转质量转换系数；A—迎风面积。

3 模型预测控制能量管理策略

3.1 模型预测控制方法

模型预测控制的流程可分为预测模型、滚动优化和反馈校正，由于其滚动优化的特点，也叫作滚动时域控制。在tk时刻时，控制器预测未来Lp时间内的变量，通过优化算法对这Lp时间内的变量进行最优控制求解，选取其中的Lc个控制量作为未来Lc时间的实际控制量。在下一步的预测过程中，继续进行同样的优化，根据实际控制量作用在运动部件产生的结果，将其反作用于控制器，达到反馈校正的效果[7]。模型预测控制能量管理策略需要首先对未来某段时域的车速做出预测，再采用动态规划算法做最优求解，选取控制量，然后依次重复车速预测、优化求解，最终得到结果。

3.2 工况预测模型

3.2.1 基于马尔可夫的工况预测模型

马尔可夫性质是指，当一个随机过程在给定过去所有状态时，其未来状态的条件概率分布只取决于当前的状态。驾驶员实际驾驶汽车时，车速变化跟外部环境、驾驶员驾驶风格相关，变化规律难以获取，其实就是一个随机过程[8]，这种随机特性过程也叫马尔可夫过程。对工况的预测即指车速预测，基于马尔可夫的工况预测可以通过以下步骤建立：

（1）利用一定量的样本数据统计由当前速度向下一时刻加速度转移的变化信息，选择标准循环工况作为样本，将速度及加速度离散为有限个区间。

（2）统计相同速度的次数mi，再统计相同速度vi分别对应的不同加速度aj的次数mj，利用最大似然估计法，便可计算出车速向下时刻加速度转移的转移概率：

不同车速下对应的转移概率组成的转移概率矩阵即是我们的预测模型。

（3）对于多阶马尔可夫预测模型，只需加入更多的速度信息即可，计算公式为：

即当车速序列是v1=vi，v2=vi-1，…，vk=vi-k+1时，i+1 时刻加速度a=aj的概率。这样，在给定任意车速时，通过马尔可夫转移概率矩阵就可以计算下一时刻的车速，依次不断重复就能得到未来某段时域的车速。

3.2.2 基于神经网络的工况预测模型

为了进一步提高车速预测的精度，利用径向基函数神经网络和广义回归神经网络进行速度预测，为后期优化提供前提[9]。神经网络的输入Vin可以包含多种信息，例如速度、加速度、坡道等，由于历史速度的组成的车速序列的差值即是加速度信息，故选择车速或加速度其一即可，将过去某段时域的车速作为神经网络预测模型的输入，表示为：

式中：Lh—过去车速的向量长度，即我们想要选取多少秒的历史车速作为输入。对应的Vout表示为：

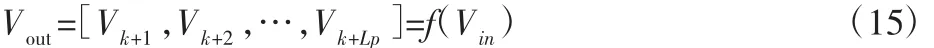
式中：f（）—神经网络的映射函数，表示对应样本输入和输出的某

种规律；Lp—预测时域长度。

通过对过去车速信息输入及其对应输出的训练，可以得到神经网络预测模型，这时只要给出指定的车速序列，就可以计算出对应的车速输出，也就是未来某段时间的车速。

3.3 目标函数及约束

模型预测控制的目标是为了让油耗能在预测时域内最优，从而得到整体较优的结果。其目标函数由油耗代价函数和与SOC相关的附加代价函数组成，表示为：

式中：α—维持SOC 平衡的惩罚因子；SOCdes—目标SOC；lSOC用于反馈控制，使状态量SOC 逼近目标值。

其约束条件为：

式中：ωe_k、Te_k、ωMG1_k、TMG1_k、ωMG2_k、TMG2_k—第K 步发动机的转速、转矩，MG1 的转速、转矩，MG2 的转速、转矩；Pbat_charge、Pbat_discharge—电池充、放电功率限制。

3.4 模型预测控制的求解

模型预测能量管理策略的优化实质是一个带约束的多目标优化问题，选择全局动态规划的方法在预测时域内进行优化求解，结合目标函数约束的反馈控制，以得到最优的控制量。

4 仿真分析

利用Matlab 软件编写m.脚本文件，完成模型预测能量管理的仿真分析。以混联式混合动力汽车丰田Prius 为原型车，其主要参数，如表1 所示。

表1 丰田Prius 混合动力汽车主要参数Tab.1 Main Parameters of Toyota Prius

预测能量管理仿真时的预测时域和控制时域分别选择了10s 和3s，选择多个标准工况组合成训练样本，另选择训练样本之外的UDDS 工况作为测试工况，工况图，如图5 所示。仿真过程中，分别应用了3 种不同阶数的马尔可夫和2 种神经网络两类预测方法，并结合预测能量管理进行了对比分析。仿真对比主要包括：工况的预测效果；控制时域内预测车速和实际车速间的均方根误差（RMSE）；UDDS 工况下的最终油耗（L/100Km），仿真结果，如图6、表2 所示。1 阶马尔可夫的预测结果，由于状态离散区间划分很细，下一秒加速度值很小，故预测时域内的车速预测值变化不大，且并未反映真实车速信息，如图6（a）所示。3 阶马尔可夫的预测结果，预测车速相比1 阶马尔可夫有了较大的改善，已经能够反映一定的车速变化信息，但整体波动幅度较大，有很多与实际值相差较大的预测值，如图6（b）所示。而图6（c）中的神经网络预测结果相比而言，预测车速轮廓更贴合实际车速，且整体波动较小，预测已经达到了不错的效果。

图5 样本及测试数据图Fig.5 Sample Data and Test Data

图6 不同能量管理预测结果图Fig.6 Prediction Results of Different EMSs

RMSE 值可反映出不同工况预测方法的精度，2 阶马尔可夫和RBF 神经网络预测结果分别次于3 阶马尔可夫和GRNN 神经网络，而又分别优于1 阶马尔可夫和3 阶马尔可夫，故不再图示，如表2 所示。

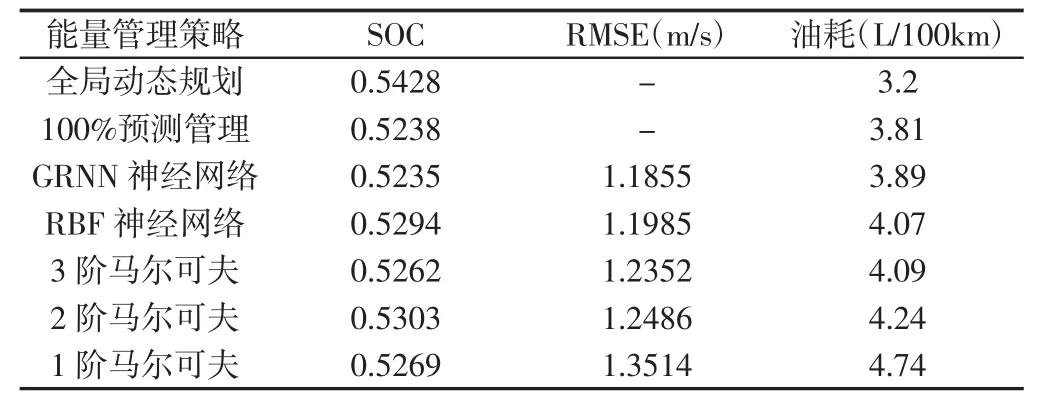
表2 不同能量管理下UDDS 工况结果对比Tab.2 Results Comparison of UDDS Under Different EMSs

由于全局动态规划优化算法在模型预测中只运用在预测时域内，无法保证整个UDDS 工况最优，故终值SOC 并没有回到初始位置。为了比较不同的油耗和SOC，加入了能量补偿的方法[10]，以GRNN 神经网络为基准，通过换算得到同一终值SOC 时的油耗，故表2 中的油耗均为换算后的值。

表中的前2 种能量管理策略是作为模型预测控制的比较参考，动态规划是在已知了UDDS 工况数据的全局优化，而100%预测能量管理是假设预测的10s 车速是完全正确的，再用模型预测的方法计算出结果。

表2 中，采用动态规划的算法由于其全局寻优的特性取得了最好的燃油经济性，而采用预测能量管理由于其优化只在预测时域内，未进行全局优化，其结果只有3.81L/100Km，相较全局动态规划其油耗增加了19%。随着马尔可夫阶数的增加，其RMSE值随之减小，表明预测的车速精确度在提升，其百公里油耗也随之减小，而SOC 三者变化不大，可见高阶马尔可夫虽建模复杂，但预测精度得到了提高，3 阶马尔可夫相较100%预测能量管理器油耗增加了约7.3%。GRNN 相较RBF 神经网络RMSE 值更小，即精确度更高，而油耗也更小，虽然终值SOC 相比较低，但是从换算后的油耗来看，仍然优于RBF，而其相较100%预测能量管理油耗增加了2.1%，相比3 阶马尔可夫预测能量管理油耗减少了4.9%。

综合来看，GRNN 神经网络油耗是最为接近100%预测能量管理策略的，相比1 阶马尔可夫提升了约17.9%的燃油经济性，表明该预测能量管理策略具有明显的节油效果。

马尔可夫预测模型随着阶数增加建模越复杂，但是建立好转移概率矩阵之后，工况在线预测时长就会大大减小；神经网络在训练模型时，由于具有大量数据，故处理起来需要的时间也长，但训练好之后，输入和输出的响应就会变得极快。由于车速预测的快速性，马尔可夫和神经网络预测模型在与预测能量管理相结合后均具有一定的实时应用潜力。

5 结论

建立了3 种不同阶数马尔可夫与2 种神经网络作为模型预测能量管理的预测模型，并采用动态规划作为滚动优化部分的优化算法，完成了对不同能量管理方法的研究。通过仿真得出，基于GRNN 神经网络的模型预测能量管理方法具有较高的工况预测精度，能够逼近动态规划算法的最优性，而且具有一定的实时应用潜力，为后期实车能量管理策略的应用打下基础。