新型防突机构对封隔器胶筒密封性能影响研究

潘 波，伍 伟，黎德才，罗 豪

（1.西南石油大学南充校区工程训练中心，四川 南充 637001；2.西南石油大学机电工程学院，四川 成都 610500；3.西南石油大学工程学院，四川 南充 637001）

1 引言

封隔器是油气井下开采的重要分层封隔工具[1]。以压缩式为主的封隔器主要依靠密封元件胶筒在轴向载荷下，发生径向膨胀，使胶筒与套管相互作用产生足够大的接触应力，密封油套环空，从而达到封隔产层以及防止层间流体和压力相互扰动等作用[2]。轴向载荷足够大时，胶筒端部会从封隔器和套管间隙中挤出产生“肩突”现象，胶筒易被撕裂损坏，降低封隔器的密封性能。为此，合理的防突机构有助于保证封隔器胶筒的密封性和完整性。

目前，国内外学者针对封隔器胶筒防突问题提出了多种防突机构，文献[3]提出整体伞形保护环防突机构，分析了伞形保护环对胶筒突出变形的影响；文献[4]将金属圆环安装在封隔器的锥形底座上，起到防突的效果；文献[5]设计了可分离防突环结构的防突机构，有效提高了胶筒的接触应力。文献[6]设计了一种蜗形状防突装置和伞式防突装置，分析了对胶筒封隔性能的影响；由于这些防突机构均置于胶筒外部，受环空砂砾等杂质影响易失效[7]，并且胶筒与防突机构末端接触位置容易应力集中，防突机构没有起到最佳效果。

为了进一步提高防突机构可靠性，在胶筒两端内部采用冷硫化胶粘剂硫化“O”形圆环截面的金属骨架作为胶筒的防突机构，在进行胶筒橡胶材料本构实验的基础上，建立了封隔器密封机构的仿真模型，开展防突机构安装位置和形状大小对封隔器胶筒密封性能的影响规律研究，防突机构的优化设计对改善封隔器的密封性能具有重要意义。

2 橡胶本构理论

封隔器胶筒材料由氢化丁腈橡胶制成，具有超弹性。描述橡胶材料超弹性的方法主要分为两大类：一类是基于热力统计学的方法，包括Arruda-Boyce 模型、Van der Waals 模型，另一类是基于橡胶为连续介质的唯象学描述方法，包括Polynomial 模型、Ogden 模型[8]。

Arruda-Boyce 形式[9]应变能密度函数：

采用万能材料试验机进行橡胶材料的单轴拉伸和单轴压缩实验，将得到的氢化丁腈橡胶应力-应变实验数据导入ABAQUS软件进行拟合，拟合曲线，如图1 所示。

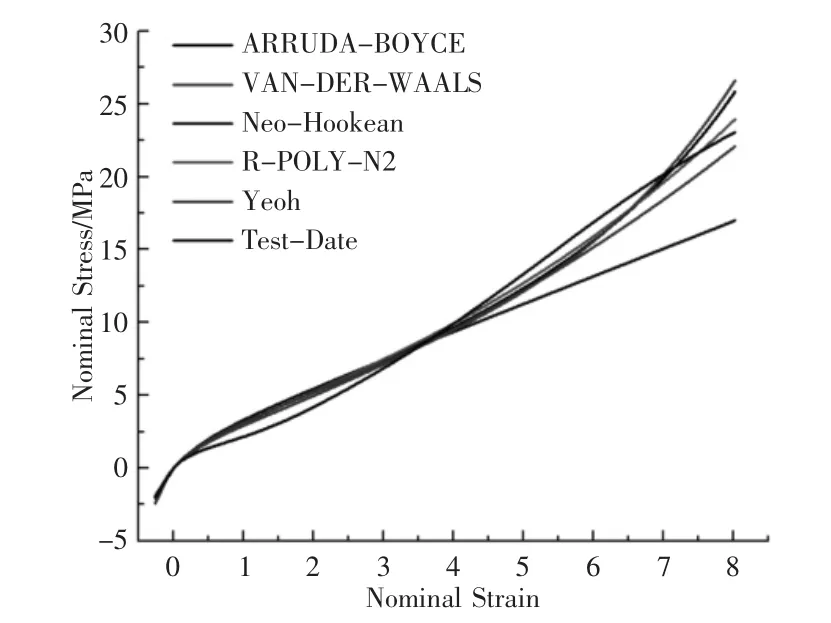
图1 实验数据与本构模型拟合曲线Fig.1 The Fitting Curves of Experimental Data and Constitutive Models

优选精度最高的二阶减缩多项式模型，材料的参数为C10=0.869147222，C20=2.916611649E-03。

3 封隔器有限元模型建立

封隔器的几何结构及所受约束和载荷是轴对称的，为缩短计算成本，对封隔器模型进行二维简化，把套管、中心管和下隔环完全固定，为比较封隔器胶筒在不同坐封载荷下的密封性能差异，在上支撑环表面依次施加（20～40）MPa 的阶梯载荷。胶筒和套管、中心管及隔环之间的摩擦因数为0.3，隔环与中心管之间摩擦系数为0.1。胶筒网格采用CAX4RH 单元，其余部件采用CAX4单元划分网格，常规和新型封隔器网格模型分别，如图2 所示。除胶筒外，其余部件的材料参数，如表1 所示。

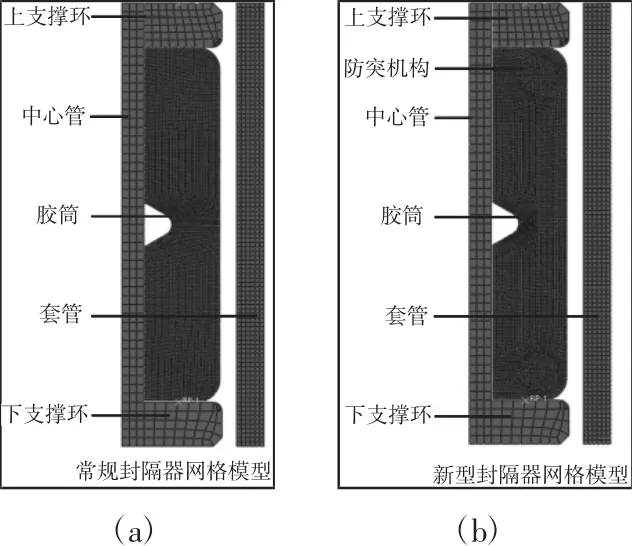
图2 封隔器有限元网格模型Fig.2 Finite Element Mesh Model of Packer

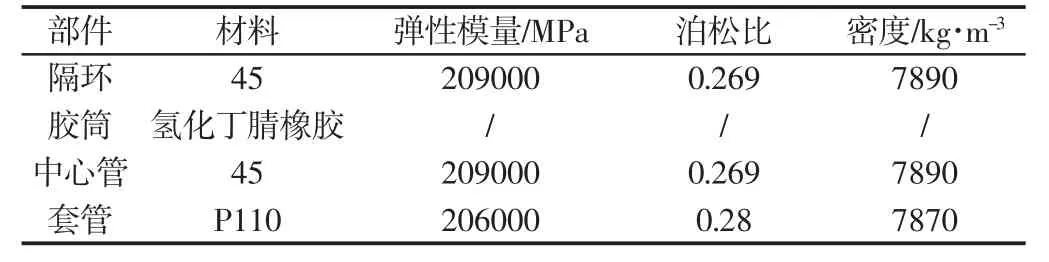
表1 封隔器模型材料力学参数Tab.1 Material Mechanical Parameters of Packer Model

4 防突机构优化分析

为避免胶筒肩突现象的产生，通过采用冷硫化胶粘剂在胶筒内部硫化的“O”形圆环截面的金属骨架，以增强胶筒的局部刚度，减少胶筒的挤出量，避免胶筒在上下端部发生“肩突”现象，改善封隔器胶筒的密封性能，如图3 所示。骨架材质选用06Cr19-Ni10 合金钢，弹性模量210GPa，泊松比为0.3，外半径为R=5mm，内半径r=4mm。

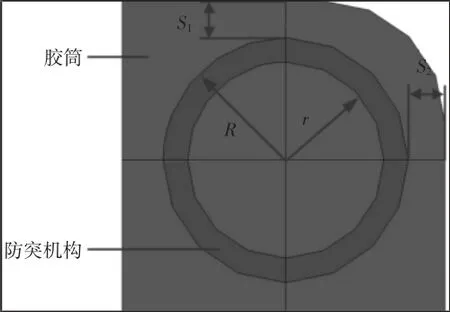
图3 防突机构二维模型Fig.3 Two-Dimensional Model of Anti-Extrusion Device

式中：S1=S2—防突机构距端面距离；R—金属骨架外径；r—金属骨架内径

4.1 金属骨架距端面距离影响

分别设定骨架距端面距离分别为0mm，0.5mm，1mm，1.5mm，以坐封载荷为40MPa 为例，得到沿套管路径的接触应力曲线，如图4 所示。不同骨架位置套管的接触应力的分布规律基本相同，最大接触应力主要集中在胶筒与套管接触的上部，沿着轴向路径逐渐降低。当金属骨架距端面的距离逐渐增大时，胶筒与套管间的接触应力逐渐降低。胶筒在不同坐封载荷下的最大接触应力曲线，如图5 所示。随着坐封载荷的增大，接触应力基本呈线性增加，但同等坐封载荷下，距端面越近，胶筒的接触应力越大，即S=0mm 时最大，其余三个位置相对下降了5.56%、6.72%、9.18%。坐封载荷40MPa 时不同金属骨架位置胶筒的Mises 应力云图及不同坐封载荷下胶筒的最大Mises 应力曲线分别，如图6、图7 所示。可以看出胶筒的应力分布大致相同，最大Mises 应力出现在金属骨架与橡胶接触位置处，加入金属骨架后，胶筒均未出现“肩部突出”现象，随着坐封载荷的增加，金属骨架硫化在胶筒内部的胶筒结构Mises 呈线性增加，40MPa 时，金属骨架与胶筒端面距离为0 时会使胶筒的Mises 应力显著增大，当金属骨架距端面距离为0.5mm 时，胶筒的Mises 应力最小，此时胶筒更安全可靠。

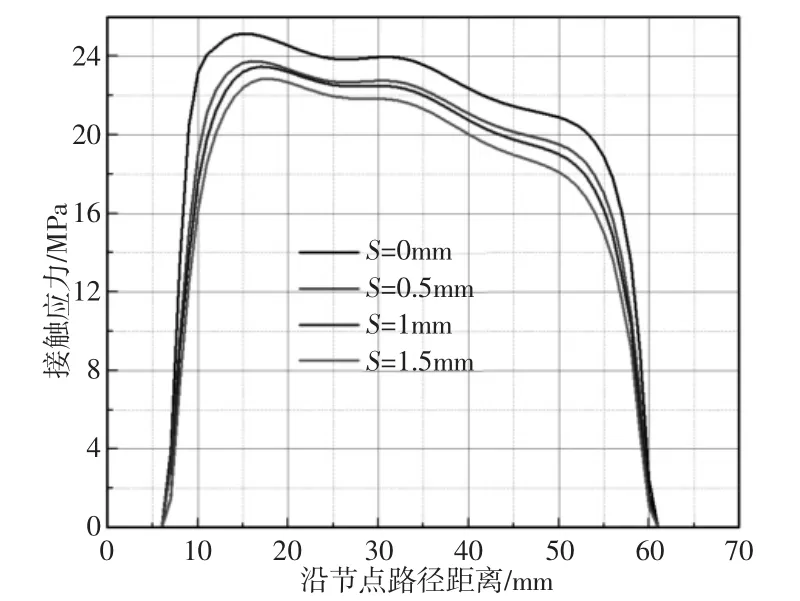
图4 不同骨架位置胶筒沿套管路径的接触应力曲线Fig.4 Contact Stress Curves of Rubber Along Casing Path with Different Skeleton Positions

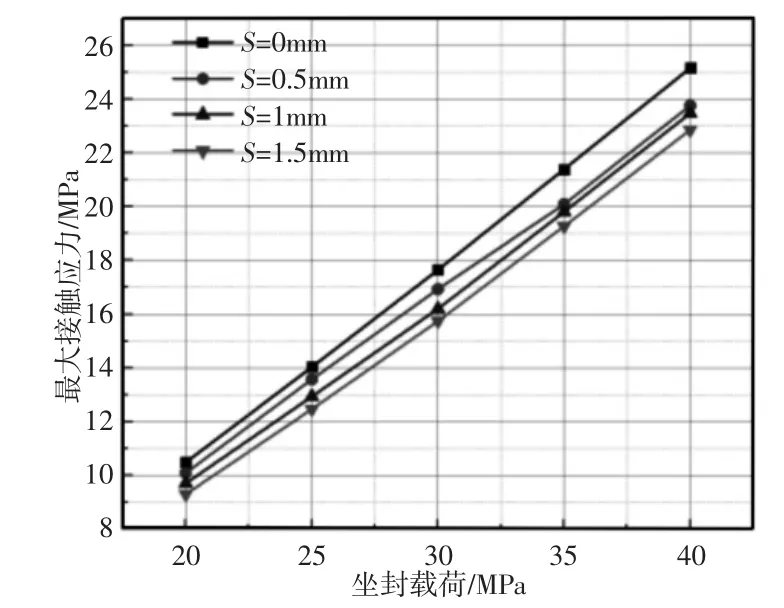
图5 不同骨架位置胶筒的最大接触应力曲线Fig.5 Maximum Contact Stress Curves of Rubber Along Casing Path with Different Skeleton Positions

图6 不同骨架位置胶筒的Mises 应力云图Fig.6 Maximum Mises Stress Nephograms of Rubber with Different Skeleton Positions

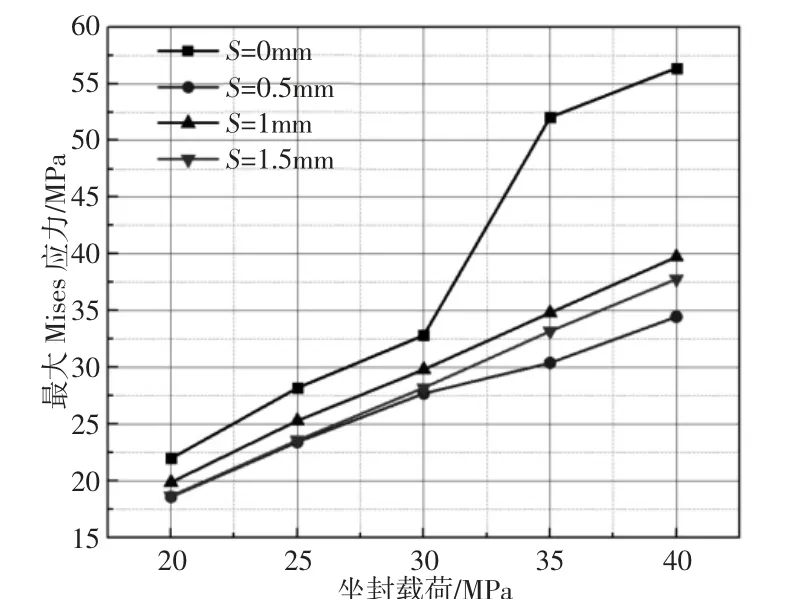
图7 不同骨架位置胶筒的最大Mises 应力曲线Fig.7 Maximum Mises Stress Curves of Rubber with Different Skeleton Positions

故金属骨架距端面距离S=0.5mm 时，接触应力基本不变，而胶筒的安全性也得到了显著提高，所以后续研究金属骨架内径对胶筒密封性能的影响时，设定金属骨架距端面距离S=0.5mm。

4.2 金属骨架内径影响

为研究骨架内径对封隔器密封性能影响，取骨架内径分别为3mm，3.5mm，4mm，4.5mm，以坐封载荷为40MPa 为例，得到沿路径的接触应力曲线图，如图8 所示。可以看出不同金属骨架内径的胶筒与套管接触的面积基本相同；随着金属骨架内半径增大，接触面的接触应力先减小后增大，在r=3.5mm 时接触应力最小，r=4.5mm 时接触应力最大，但接触应力沿着轴向方向下降较快，这是由于当骨架内半径增大时，骨架的厚度就变小，导致胶筒端部的刚度降低，胶筒的接触应力集中在端部与套管的接触面上。

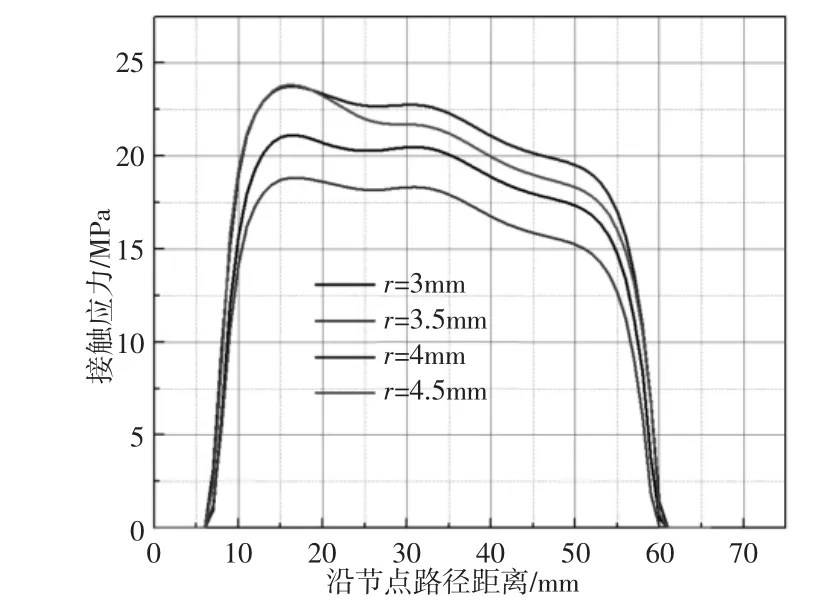
图8 不同骨架内径胶筒沿套管路径的接触应力曲线Fig.8 Contact Stress Curvesof Rubber Along Casing Path with Different Skeleton Inner Diameters

在不同坐封载荷下，不同骨架内径胶筒的接触应力曲线，如图9 所示。可以看出当坐封载荷小于30MPa 时，不同金属内径的胶筒接触应力均近似相等，当坐封载荷大于30MPa 时，随着金属骨架的内半径增大，接触应力先降低后升高，在r=3.5 时最小，r=4mm 时最大。40MPa 下不同金属骨架内径胶筒的Mises 应力云图及不同坐封载荷时胶筒最大Mises 应力曲线分别，如图10、图11所示。可以看出胶筒的应力分布大致相同，在靠近金属骨架和凹槽位置应力更大，随着金属骨架内径的增大，胶筒的最大Mises 应力会发生上下波动，当r=3.5mm 时胶筒应力最小，当r=4mm 时胶筒应力最大。故金属骨架内径r=4.5mm 时，接触应力基本不变，而胶筒的安全性也得到了显著提高，因此骨架的内径最佳为4.5mm。

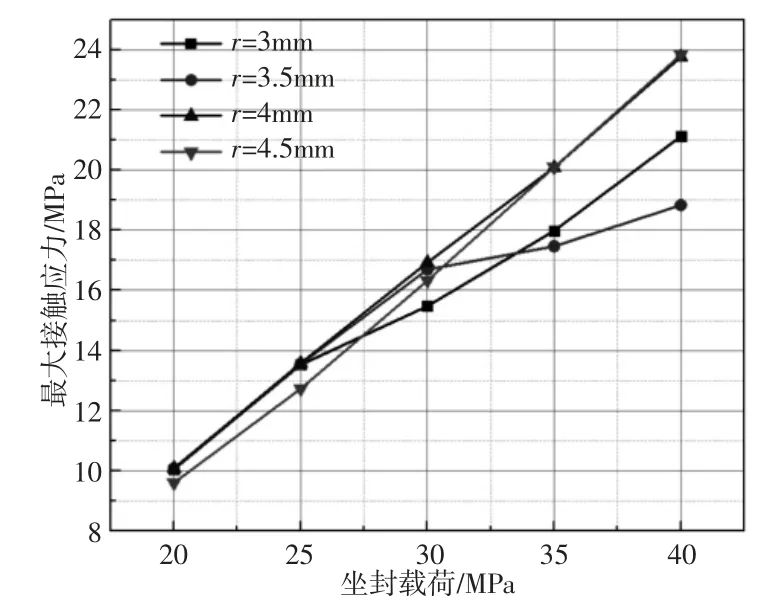
图9 不同骨架内径胶筒的最大接触应力曲线Fig.9 Maximum Contact Stress Curves of Rubber with Different Skeleton Inner Diameters

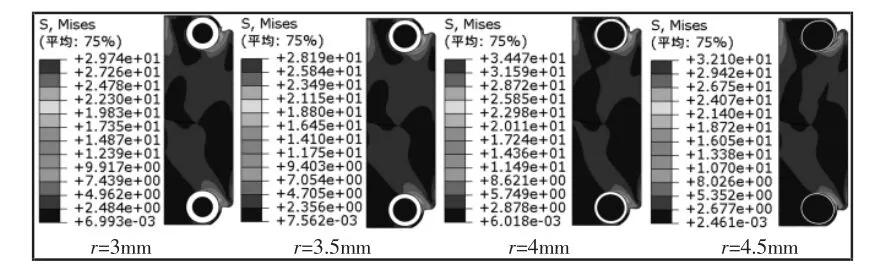
图10 不同骨架内径胶筒的Mises 应力云图Fig.10 Mises Stress Nephograms of Rubber with Different Skeleton Inner Diameters

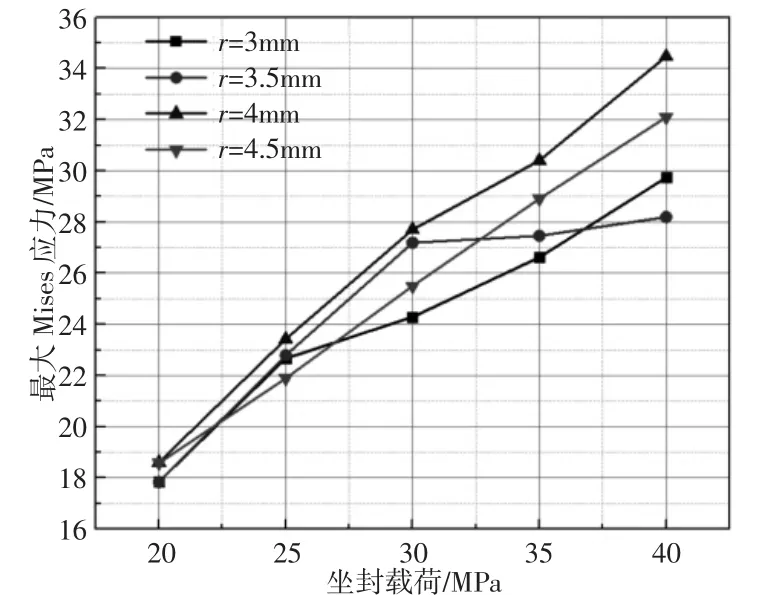
图11 不同骨架内径胶筒的最大Mises 应力曲线Fig.11 Maximum Mises Stress Curves of Rubber with Different Skeleton Inner Diameters

5 结论

（1）开展了胶筒橡胶材料的本构实验，优选出表征胶筒材料的力学性能的本构模型为二阶减缩多项式模型。（2）设计的新防突机构有效地避免胶筒肩突现象的产生，改善了胶筒接触应力和Mises 应力的分布规律。（3）随着坐封载荷的增大，胶筒接触应力、Mises 应力增大，金属骨架外半径R=5mm，内半径r=4.5mm，距端面位置S=0.5mm 时胶筒的密封性能最佳。