漏斗车触碰式底门开闭机构分析

方 吉，申金鹏，丁洪钧，李晓峰

（1.大连交通大学机车车辆工程学院，辽宁 大连 116028；2.中车齐齐哈尔车辆有限公司，黑龙江 齐齐哈尔 161000）

1 引言

底门开闭机构是铁路漏斗车非常重要的快速卸货工具，历年来由于设计等原因导致在运行途中出现底门打不开、关不上或意外打开等意外情况，给铁路货运造成不利的影响[1-3]。为了避免类似情况的发生，在底门开闭机构的设计过程中需要对其传动机构进行运动学与动力学分析。为了考察漏斗车底开门机构能否实现预期的基本动作，首先建立漏斗车底开门机构的多体仿真模型进行运动学仿真，分析其各部件运动学关系，验证该机构的可行性。施加货物载荷，进行触碰开门及关门动力学过程计算，并校验关键部件的稳定性及强度。

2 建立多体动力学模型

利用MSC.ADAMS 多体系统动力学软件建立漏斗车底门开闭机构动力学模型[4]，漏斗车底开门机构主要由底门、传动轴、短连杆、长连杆、曲杠杆、开门触碰及关门触碰装置等组成。其中开门限位块和开门及关门止挡以简化结构代替，其它主要结构均按实际设计尺寸建模，如图1 所示。

为了考察该机构是否能够实现，开门转臂与开门触台碰撞后顺利实现打开底门的基本动作，进行开门过程运动学仿真；等货物完全卸载完成后，通过关门转臂与关门触台的碰撞接触，顺利将底门关闭到死点锁紧位置。开门过程是开门转臂与开门触台短暂接触后，底门就与开门触台分离并自动开启，因此开门力指受开门触台的接触面倾斜度影响，而开门触台高度对开门力影响很小，主要影响发生接触时间。

在关门过程中，关门转臂滑轮最终必须越过关门触台顶面，因此关门触台顶面与关门转臂滑轮底面的相对高度对关门接触力起决定性影响。为了保证底门安全的关门到位，实际设计过程中会在此处预留高度过盈量，高度过盈量太小不利于关门到位，太大则造成关门力及结构内载荷过大可能造成结构的强度不足，因此需要拟定一个合适的取值[5]。本次计算取20mm 的高度过盈量（即在关门转臂滑轮经过关门触台最高顶面时，由于存在弹簧关门触台最高顶面会被下压20mm）。

图1 漏斗车底门开闭机构多体系统动力学模型Fig.1 Multi-Body System Dynamics Model of HopperCar Opening and Closing Mechanism

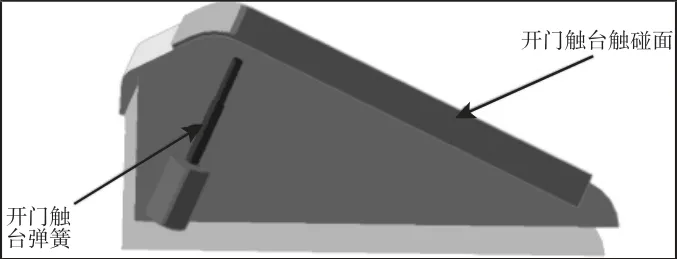
图2 正向开门触台模型Fig.2 Forward Opening Contact Model

图3 正向关门触台模型Fig.3 Forward Closing Contact Model

图4 反向关门触台模型Fig.4 Reverse Closing Contact Model

其中开门触台只有一种形式，如图2 所示。其接触方式分正向开门和反向开门两种，关门触台的正向关门和反向关门过程分别采用两种不同的触台形式，如图3、图4 所示。在ADAMS/View 中接触力的求解方法有下面两种：（1）补偿法需选择合适惩罚系数与补偿系数，设置的惩罚系数越大则嵌入体积越小，此时的接触刚度越大；（2）冲击函数法是利用软件函数库中的Impact 函数进行接触力的计算，所需构件嵌入时生成的弹性力和物体间相对速度生成的阻尼力这两部分。采用冲击函数法定义滑轮与开门触台之间的接触，如图5 所示。

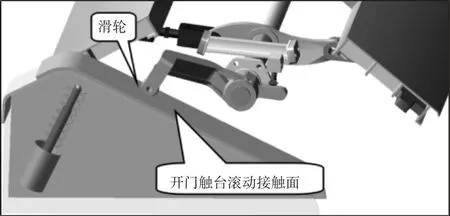
图5 滑轮-开门触台接触模型Fig.5 Contact Model of Opening Contact Table

接触可以分为法向接触与切向接触。其中切向接触的摩擦求解较为复杂，通常分为动摩擦和静摩擦[6]。

法向接触力的广义表示形式为：

式中：K—赫兹接触刚度；δi—法向的穿透深度；C—阻尼系数，计算过程中选取合适的接触阻尼参数可以使得接触面处的振动快速收敛，如图6 所示；e—力的指数，该车滑轮与移动轨道为钢材料之间的接触，取值为1.5；Vi—法向相对速度[7]。

图6 阻尼与穿透深度曲线Fig.6 Damping and Penetration Depth Curves

3 传动受力分析

首先是漏斗车底门上载荷的确定，根据底门正上方的货物重量来计算垂向载荷，单个底门上货物：3.04t×1.56（相关系数）=4.74t。重力：4.74t×9.8=4.65E4N，施加方向为竖直向下，在开门过程中力的方向始终向下，载荷的施加在底门的几何中心处。钢结构密度取7850kg/m3，根据各部件的几何模型，计算质量、质心位置、转动惯量等动力学参数。钢对钢动摩擦系数取0.15，静摩擦系数0.2，开门触台及关门触台的移动速度设定0.5m/s，考虑到关门过程中底门上货物已经卸载完毕，底门上载荷定义时间历程定义，如图7 所示。

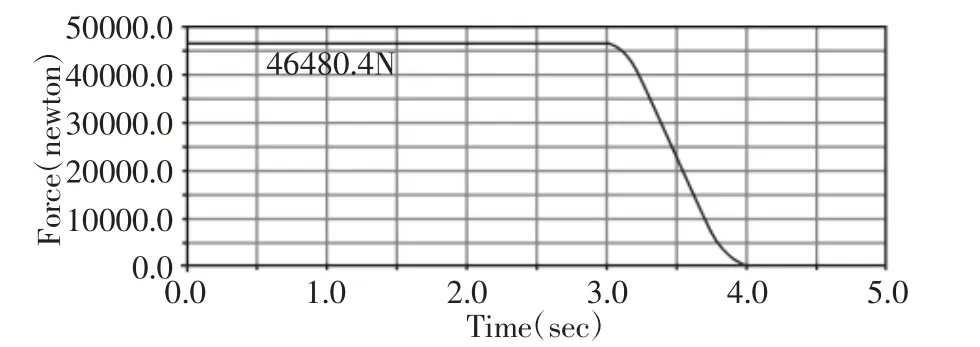
图7 底门上货物载荷的定义Fig.7 Definition of Load on the Bottom Door

3.1 准静态受力分析

图8 底门机构受力简化模型Fig.8 Simplified Model of Door Mechanism

该底开门机构基本结构类似于一个双四杆机构，如图8 所示。其中左侧门、长拉杆、中心转轴及车体构成四杆机构，另外右侧门和短连杆中心转轴及车体另外一套四杆机构，其中中心转轴是公共的部件。在做仿真计算前，建立一个简化的力学模型进行计算是有必要的，其计算结果判断仿真结果是否可靠的一个重要依据。由于在开门阶段，底门上存在货物载荷作用，因此，只有将开门触台的斜面角度设计与图8 中开门力方向垂直才能有效的减少开门所需触碰力。

其中，货物载荷包括底门和货物的自重F1=47793.6 牛顿，载荷力臂L1=256.7mm，左拉杆力臂L2=345.2mm，右拉杆力臂L3=330mm，中心轴左侧力臂L5=20mm，中心轴右侧力臂L4=22mm。开门砖壁的力臂L6=278mm，忽略摩擦力和惯性力，可以通过下面静平衡方程计算获得开门驱动力。

通过式（2）～式（4）的计算可获得开门所需驱动力F 为5499.0N，简化公式计算的结果是近似的，由于没考虑惯性力和摩擦力，计算结果应该比实际情况要小一些，可以用来校核仿真计算的结果是否可靠。开门所需的最大载荷理论上应该是在启动阶段，启动之后最大静态摩擦系数变成动摩擦系数之后所需开门力会小一些，当开门转臂越过四杆机构死点位置之后门在重力作用下底门自动开门。

3.2 正向开门过程受力仿真分析

当开门触台与开门转臂接触，打破自锁死点状态之后系统会因货物重力自动开门。底门打开后，货物会自动卸载，底门上的载荷会不断减少，然后底门撞击开门限位装置并停下来。在1.82s 时刻，开门触台与开门转臂发生接触；2.10s 门完全打开，底门与开门限位块发生接触。其中开门止挡块、开门转臂、长连杆、短连杆、弹簧挡座受力时间历程，如图9～图13 所示。最大受力，如表1 所示。

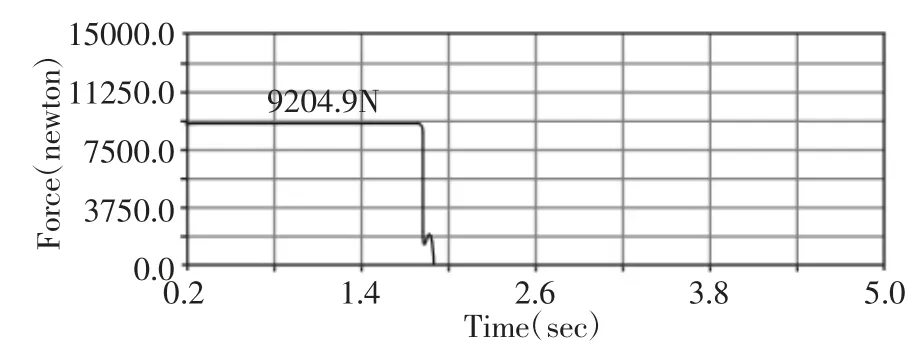
图9 单个开门止挡块受力过程Fig.9 Reaction Force on Single Door Stop Block

图10 开门转臂的接触合力Fig.10 Contact Force of the Door Open Arm

图11 长连杆所受合力Fig.11 The Reaction Force of the Long Link

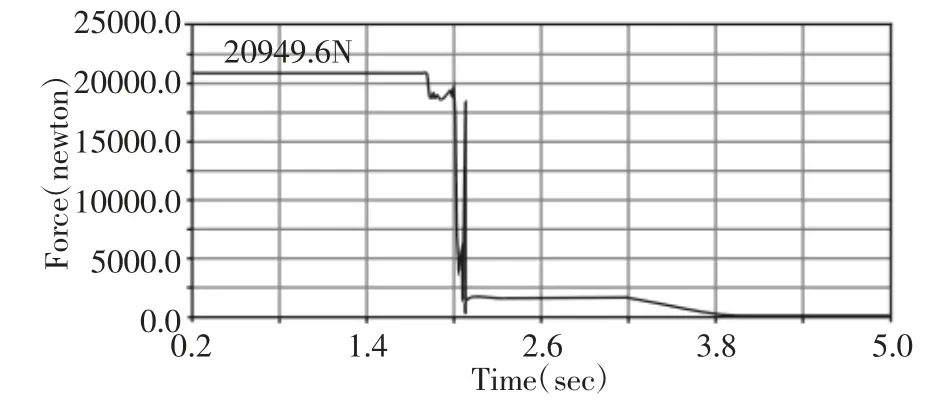
图12 短连杆所受合力Fig.12 The Acting Forces of the Short Connecting Rod

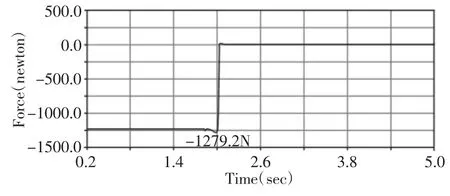
图13 单个弹簧挡座的受力Fig.13 Force on Single One Spring Seat

表1 正向开门过程受力汇总Tab.1 Force Summary of the Positive Opening Process

3.2 反向开门过程受力仿真分析

当开门触台撞击开门转臂，打破系统自锁的死点状态，系统会因货物重力自动开门，底门打开后，货物会自动卸载，底门上的载荷会不断减少，然后底门撞击开门限位装置并停下来。在1.36s时刻，开门触台与开门转臂发生接触；1.66s 门完全打开，底门与开门限位块发生接触。其中开门转臂所受接触合力，如图14 所示。最大受力汇总，如表2 所示。

图14 开门转臂的接触合力Fig.14 Contact Force of the Door Open Arm

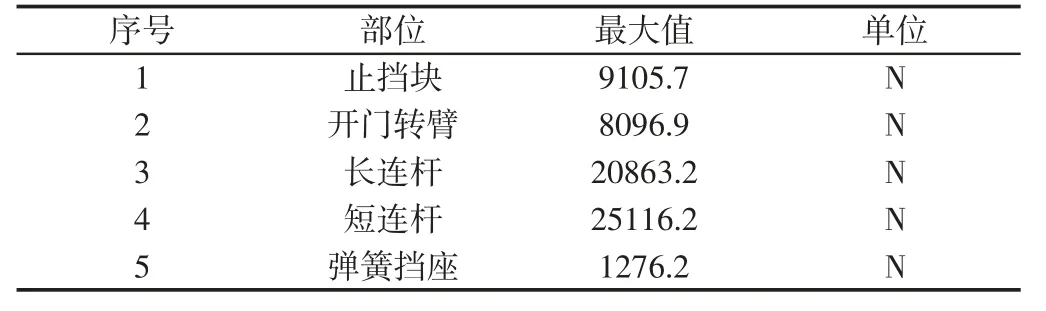
表2 反向开门过程受力汇总Tab.2 Summary of Forces in Reverse Opening Process

3.3 正向关门过程受力仿真分析

由于关门过程中，关门触台的高度对结构受力影响很大，如果关门高度过高，当门已经关闭到位，触台将继续对结构施加载荷，使结构产生额外的内力作用。本次计算采用关门触台顶面与关门转臂滑轮底面间有20mm 的高度过盈量，在关门触台与地面之间安装弹簧，弹簧刚度225N/mm。关门触台的纵向移动速度为0.5m/s，在5.62s 时刻，关门触台开始与关门转臂产生接触，在9.69s 关门到位并稳定下来。其中开门转臂的接触合力，如图15所示。关门触台弹簧压缩量，如图16 所示。最大受力见汇总，如表3 所示。

图15 关门触台与关门转臂的接触合力Fig.15 Contact Force Between Door-Closing Contact Platform and Door-Closing Rotating Arm

图16 关门触台弹簧压缩量Fig.16 Spring Compression of Closing Contact Platform

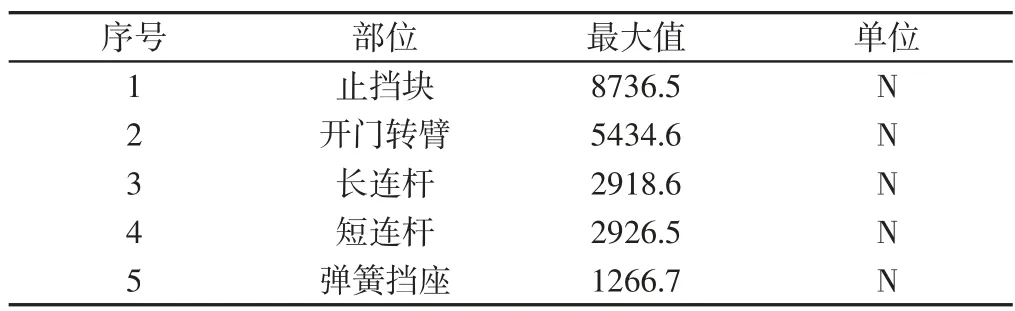
表3 正向关门过程受力汇总Tab.3 Forces Summary of Parts during Forward Closing

3.4 反向关门过程受力仿真分析

同正关门过程关门触台顶面与关门锁紧位关门转臂滑轮底面间有20mm 的高度过盈量，在关门触台处增加弹簧，弹簧刚度225N/mm。关门触台的纵向移动速度为0.5m/s，在5.53s 时刻，关门触台开始与关门转臂接触，在9.63s 关门到位并稳定下来。其中开门转臂所受接触合力，如图17 所示。最大受力汇总，如表4所示。

图17 关门触台与开门转臂的接触合力Fig.17 Contact Resultant Force Between Closed Contact Platform and Open Revolving Arm

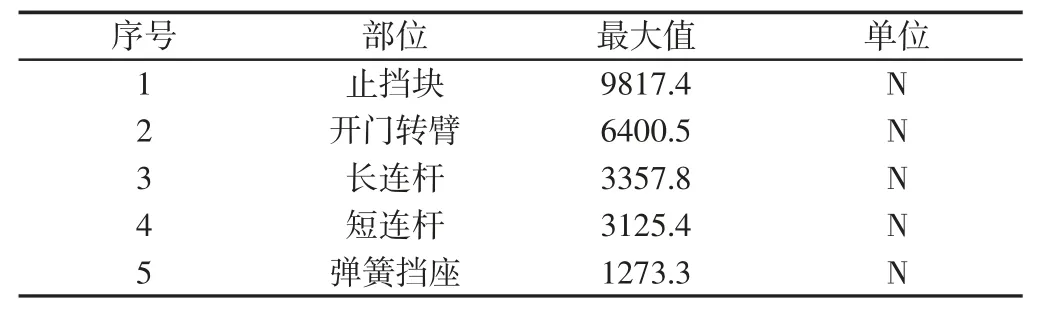
表4 反向关门过程受力汇总Tab.4 Forces Summary of Parts in Reverse Closing Process

4 关键部件强度及稳定性分析

从前面的动力学分析可以看出四种仿真模拟过程中反向开门过程受力最大，因此主要以反向开门过程的受力来校核各部件的强度是否满足要求[8]。其中长连杆属于二力杆属于是细长结构，主要承受轴向压力作用且载荷较大，所以有可能会出现失稳，因此除了需要强度计算外还需要对其进行屈曲稳定性计算。曲杆、开门转臂和关门转臂做强度计算即可。传动轴受力比较复杂，且结构中心部分是空心的，所以按开门最大扭矩并考虑两个不同位置曲杆均匀受载和远端单侧受载的极限工况来分别校核其强度[9]。长连杆有限元模型，如图18 所示。最大的峰值载荷为20863.2N，平行于连杆轴线的压力，最大应力为39.3MPa，最大位移为0.07mm，满足应力不超过216MPa 的标准要求，如图19 所示。长连杆屈曲稳定性的第一阶失稳振型，如图20 所示。当载荷大于或等于6.0856E5N 时，结构可能出现如下的弯曲失稳[10-11]。动力学计算结果中该杆最大受力为20863.2N 力小于6.0856E5N，所以安全。

图18 长连杆有限元模型Fig.18 Finite Element Model of Long Connecting Rod

图19 长连杆应力分布Fig.19 Stress Distribution of Long Connecting Rod

图20 长连杆屈曲稳定性系数Fig.20 Buckling Stability Coefficient of Long Connecting Bar

短连杆最大的峰值载荷为25116.2N，平行于连杆轴线的压力，最大应力为42.9MPa，最大位移为0.03mm，满足应力不超过216MPa 的标准要求，如图21 所示。曲杆同时受短连杆和长连杆的压力作用，其中长连杆的最大的峰值载荷为20863.2N，平行长连杆轴线的压力，短连杆的最大的峰值载荷为25116.2N，平行短连杆轴线的压力，在这两个力同时作用下的强度计算，如图22 所示。最大应力为34.4MPa，最大位移为0.03mm，满足应力不超过216MPa 的标准要求。开门过程触碰最大峰值载荷进行加载（最大峰值为8096.9N），最大应力为212MPa，如图23 所示。最大位移为1.2mm，满足应力不得超过许用应力216MPa 的标准要求。关门过程触碰载荷峰值进行加载（最大峰值为6400.5N），最大应力为195MPa，最大位移为1.7mm，满足应力不得超过许用应力216MPa 的标准要求。

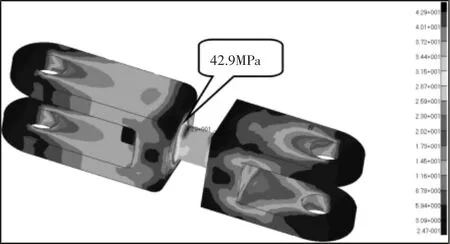
图21 短连杆应力云图Fig.21 Stress Distribution of Short Connecting Rod

图22 曲杆应力云图Fig.22 Stress Distribution of Curved Bar

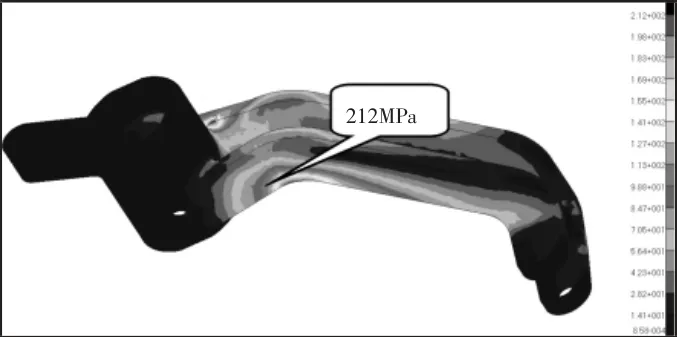
图23 开门转臂应力云图Fig.23 Stress Distribution of Open-Door Rotating Arm

图24 关门转臂应力云图Fig.24 Stress Distribution of the Closing Arm

表5 关键部件强度计算结果汇总Tab.5 Summary of Strength Calculation Results for Key Components

通过关键部件的强度计算分析，结果汇总，如表5（部件序号参见图1）所示。考虑到同一侧门的两套机构结构完全一致，由于安装误差或某些突发情况可能导致单侧受力的情况，因此将相关杆件的载荷放大为原来的2 倍进行校核，可以给出比较保守的评估结果。假设单侧受载极限情况的，等效于最大载荷放大2 倍，根基线形静力学基本理论应力放大为原来的2 倍[12]。由于传动轴应力最大位置是发生在端部轴颈部，且单侧受载或两均匀受载对传动轴的应力计算影响不大，所以应力不变；而开门转臂和关门转臂的通过仿真获得触碰力载荷本身属于单侧受载情况，因此应力也不变，且都小于216MPa，满足强度要求。长连杆除了强度满足要求外，屈曲稳定性也满足要求。

5 结论

通过漏斗车底门开闭机构的动力学仿真分析与强度计算得出的主要结论如下：（1） 通过正向与反向开关门过程的动力学仿真计算结果，正向开门所需驱动力为7182.7N，这与准静态的简化计算结果5499.0N 相对比较接近，由于准静态计算忽略惯性和摩擦力，因此计算结果比仿真计算要小一些这是符合理论的。通过对比间接的验证了仿真计算结果的有效性。（2）通过正向开门与关门过程的动力学仿真计算，可以看出开门过程整体受力比关门过程要大，由于开门过程底门上有货物载荷作用，而关门过程底门上无载荷作用，因此其主要载荷是触台高度过盈量造成的内力作用。（3）通过强度计算，可以得出短连杆、长连杆、曲杆、传动轴、开门转臂、关门转臂在动力学仿真获得的最大载荷作用下应力小于216MPa 的标准，满足强度要求，长连杆屈曲稳定性也满足要求。